高中数学立体几何教材难度的比较
陈小艳 周思波
【摘 要】 教材难度是衡量是否造成学生学业负担过重的重要指标,对教材质量的评价起着至关重要的作用,在数学中更为明显.将目前已有的刻画数学教材难度的模型直接用于高中数学教材立体几何部分难度的比较略显粗糙,缺乏针对性,因此需要对现有模型进行改进.首先分析已有的课程难度模型,然后进行优化和调整,建立一套刻画高中教材难度的量化模型,并将其应用于人教A版和北师大版立体几何部分的比较,验证了这一模型的可行性.
【关键词】 综合难度;广度;深度;教材
1 前言
数学教材作为重要的数学课程资源,是辅助教师教学的最好依据,也是帮助学生学习的最经济实效的材料,因此一本好的数学教材对教师和学生必不可少.教材难度是衡量教材质量的至关重要的因素,鲍建生教授构建了一个比较数学题难度的综合难度模型 [1],但影响数学教材难度的因素还有课程内容的广度、深度以及内容的组织呈现方式等.因此本研究基于这一模型,再在宋乃庆 [2]、史宁中 [3]、邹宏运 [4]等人建立的难度模型的基础上进行优化与调整,建立起一套适用于刻画高中数学教材难度的量化模型,希望能为教师选择教材提供依据,同时为教材编写人员提供实质性的建议.
2 综合难度模型的建构
2.1 教材难度测量维度
教材难度主要指教材呈现内容的难度,包括知识点、例题、习题以及探究思考题.通过对已有的课程难度模型的分析,发现影响教材难度的因素主要有:内容广度、内容深度、内容的呈现方式、课程时间、例题难度、习题难度等.
由于本研究只考虑教材本身的绝对难度,不关注教材与学生学习之间的相互影响,因此对课程时间这一难度因素暂不做考虑.此外,与小学教材相比,高中教材呈现方式更为单一,因此内容的呈现方式对教材难度的影响较小,也暂略去.笔者将从剩下的四个难度影响因素着手,并将其分为两个维度:内容难度和数学题难度.内容难度包括内容的广度和内容的深度;数学题则包含例题和习题.
2.1.1 内容的广度
内容的广度指的是课程内容所涉及到的领域和范围的广泛度,可以直接统计知识点的个数.需要指出的是,为了减少误差,这里只计算教材用特殊标记标明的知识点个数.
2.1.2 内容的深度
内容的深度是指对教材呈现的知识的要求水平,其抽象性決定了这一维度极难量化,这里我们根据范希尔的几何思维水平来对内容的深度进行刻画,具体如下 [5]:
水平0:直观感受.对几何图形的整体感知,不要求认识到其中的组成部分,即只停留在表面、直观.对处于这一水平的内容赋值为1;
水平1:分析水平.教材要求能够辨认或者通过构成要素之间的关系来识别图形,能利用这些特性解决几何问题,但不要求解释性质间的关系,对图形的定义也不做要求.对这一水平的内容赋值为2;
水平2:非形式演绎.教材要求能逻辑地组织概念和图形所具有的性质,并能进行一步的演绎推理,但不要求能由不熟悉的前提去证明结果的成立,也不要求建立定理网络之间的内在关系.处于这一水平的内容赋值为3;
水平3:形式演绎.对公理化系统中的未定义项、定义、公理、定理作出明确区分,并能作出一系列命题以对作为“已知条件”的逻辑结论的某个命题进行证明;但这时推理的对象还只是图形性质之间的关系,而并非不同演绎系统之间的关系.这一水平的内容赋值为4;
水平4:严密性.要求在不同的公理系统下严谨地建立公理,以分析比较不同的几何系统,如欧式几何与非欧几何的比较.将这一水平的内容赋值为5.
最后再采用所有知识点的深度取值加权平均来刻画内容的深度,也即“平均内容深度”.
2.1.3 例题和习题难度
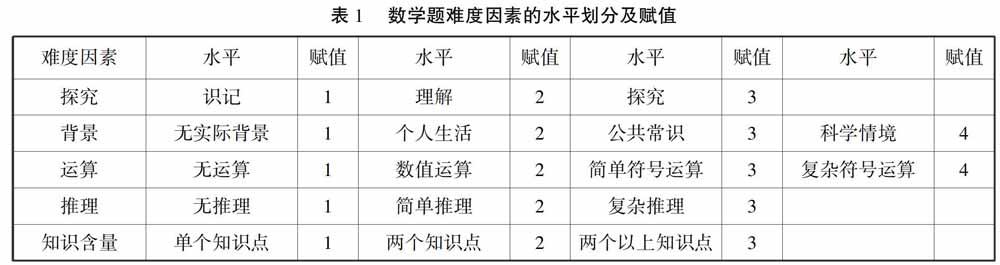
研究数学题难度的量化模型多是在鲍建生的数学课程综合难度模型上进行改进的,因此本研究直接采用鲍建生的数学课程综合难度模型来刻画例题和习题的难度.鲍建生将影响数学题的难度因素分为五个,分别是:探究、背景、运算、推理以及知识含量.然后将这些因素分为不同的水平,相应的水平赋于相应的权值,再用加权平均的方法对每个影响数学题难度的因素进行量化,具体难度因素的水平及赋值如下表:
2.2 教材难度计算方法
基于以上对影响教材难度的各个维度的分析,建立如下量化模型来刻画教材难度.首先,使用加权平均计算教材难度:N=αC+(1-α)Q.
其中,α表示教材内容对教材难度的影响程度,满足0<α<1.N指高中数学教材的难度,C指教材内容难度,Q则是数学题目(包括例题和习题)的难度.
由于数学课程的难度水平在很大程度上是由其包含的数学题所确定的 [1],再根据宋乃庆等人给出的数学教材难度模型,教材难度分为内容难度、例题难度和习题难度,这三个维度的权值分别为0.3、 0.36、0.34,所以可以得到内容难度所占的权值应为0.3,即α的取值为 0.3.
其次,内容难度也可采用加权平均来进行量化,即:
C=βG+(1-β)S.
其中,β表示内容广度对整个内容难度的影响程度,范围是0<β<1.G表示内容的广度,S表示内容的深度.对于β的具体取值,专门有文献对其分析,许多一线教师和专家也有过探讨.本研究参照的是宋乃庆等人给出的模型,由于其将内容难度分为了内容多少、内容的要求和内容呈现方式,分别取的权值是0.45、0.32、0.23.因为本研究没有考虑内容的呈现方式,所以将内容的呈现方式所占的权值均分到内容多少以及内容的要求,分别对应本研究中的内容的广度和内容的深度这两个维度中,所以最终内容的广度所占的比值是0.565,也即β=0.565.
最后是数学题难度的计算方法,量化公式为:
Q=γW+(1-γ)E.
其中,γ表示例题难度对数学题难度的影响程度,取值范围是(0,1).由于例题与习题难度的计算方法一致,都是采用鲍建生所建立的综合难度模型中采用的方法,且两者对数学题难度的影响程度接近,所以取γ=0.5.
由于例題与习题难度的计算方法一致,所以接下来只需考虑例题的计算方法即可.具体如下:
W=∑ 5 i=1 λ iw i.
其中λ i(i=1,2,3,4,5)分别表示为探究、背景、运算、推理、知识含量这5个难度因素对例题难度的影响系数,满足∑ 5 i=1 λ i=1.考虑到5个难度因素对例题难度的影响相当,所以取λ i=0.2(i=1,2,3,4,5).w i(i=1,2,3,4,5)依次表示探究、背景、运算、推理和知识含量五个难度因素上的取值,具体计算方法为:
w i= ∑ j nijwij n (∑ j nij=n;i=1,2,3,4,5;j=1,2,…).
wij表示第i个难度因素的第j个水平的权重(依水平分别取1,2,3,…),nij则是一组题目中属于第i个难度因素的第j个水平的题目的个数,和为该组题目的总数n.习题难度的计算方法类似,只需将w替换为e即可.
综上,本研究建立的刻画高中数学教材难度的模型为:
N=αC+(1-α)Q;C=βG+(1-β)S,Q=γW+(1-γ)E;
W=∑ 5 i=1 λ iw i,E=∑ 5 i=1 λ ie i;
w i= ∑ j nijwij n (∑ j nij=n;i=1,2,3,4,5;j=1,2,…),
e i= ∑ j nijeij n (∑ j nij=n;i=1,2,3,4,5;j=1,2,…).
其中影响系数α,β,γ以及λ i(i=1,2,3,4,5)的取值分别为0.3,0.565,0.5,0.2.
3 人教A版与北师大版立体几何的综合难度比较
人教A版的立体几何包括必修2中第一章的空间几何体和第二章的点、直线、平面之间的位置关系,北师大版立体几何部分则指必修2中第一章的立体几何初步,本研究基于以上刻画高中数学教材难度的模型,对人教A版与北师大这两个教材版本中的立体几何部分作一个对比分析.
3.1 内容难度的比较3.1.1 内容广度的比较
人教A版的立体几何部分包含的知识点个数是49个,北师大版包含47个,因此人教A版和北师大版的内容广度取值分别为49和47,人教A版在立体几何这一部分的内容广度要稍高于北师大版.
3.1.2 内容深度的比较
人教A版和北师大版教材中立体几何部分的知识点所要求的几何思维水平具体分布如下表:
经过计算,人教A版和北师大版的平均内容深度取值分别为102和100,因此这两个教材版本立体几何部分的内容难度如下表:
3.2 数学题难度的比较
人教A版教材的立体几何部分的数学题包含例题20个,课后练习题39个,A组习题61个,B组习题25个;而北师大版则有27个例题,46个课后练习题,57个A组习题和22个B组习题,还包括2个C组的习题.将这些题目分为例题和习题(包括练习题和习题)分别进行比较.
3.2.1 例题难度的比较
通过以上表格的分析,最终使用加权平均得到人教A版和北师大版两版教材的习题难度分别为 1.630和1.542.
3.2.2 习题难度的比较
采用与例题难度比较类似的方法比较两个教材版本习题难度,具体分析如下表:
最终得到人教A版和北师大版教材的习题难度分别为1.768和1.7904.
最后,对内容难度和数学题难度分别赋权值0.3和0.7,得到人教A版立体几何部分整体的教材难度为22.8541,而北师大版则为22.2698.
4 讨论
基于以上的研究分析,人教A版与北师大版教材在立体几何这一部分的整体难度相当,虽然人教A版的难度高于北师大版,但差异值仅为0.6,这符合我国教育所提倡的“一标多本”的实际,也说明本文所建立的量化模型用于刻画高中数学教材中立体几何部分的难度是可行的.
但由于范希尔的几何思维水平层次还未推广到代数部分,所以文中所建立的教材难度的量化模型仅仅适用于几何部分的比较.同时影响教材难度的因素也不仅仅局限于以上几种,因此对于教材难度的刻画还有待于进一步深入研究.
参考文献
[1] 鲍建生.中英两国初中数学期望课程综合难度的比较[J].全球教育展望,2002(09):48-52.
[2] 蔡庆有,邝孔秀,宋乃庆.小学数学教材难度模型研究[J].教育学报,2013(05):97-105.
[3] 郭民,史宁中.中英两国高中数学教材函数部分课程难度的比较研究[J].外国中小学教育,2013(07):55-59.
[4] 邹宏运.国内高中数学教材圆锥曲线部分难度比较研究——以“人教版”和“北师大版”为例[A].全国数学教育研究会.全国数学教育研究会2012年国际学术年会论文集[C].全国数学教育研究会:2012:20.
[5] 鲍建生,周超主编.数学学习的心理基础与过程[M].上海:上海教育出版社,2009.10.

