奇、偶项为不同数列型问题的探究
☉江苏省徐州市第三中学 赵 勇
奇、偶项为不同数列型问题的探究
☉江苏省徐州市第三中学 赵 勇
在处理奇数项与偶数项为不同类型的数列求通项公式或前n项和中,由于学生在进行奇、偶讨论时经常会错把n当成了奇数项数列、偶数项数列的项数,从而产生错解.下面通过举例,对此类问题进行详细探究,以期对学生解答此类问题有所有助,从而有效避错.
题目已知由整数组成的数列{an}各项均不为0,其前n项和为Sn,且a1=a,2Sn=anan+1.
(1)求a2的值;
(2)求{an}的通项公式;
(3)若n=15时,Sn取得最小值,求a的值.
一、通项问题
第(1)问,较为简洁,直接利用赋值法即可求解.
因为2Sn=anan+1,所以2S1=a1a2,即2a1=a1a2,因为a1=a≠0,所以a2=2.
第(2)问,给出与前n项和Sn有关的关系式,通常利用公式求解.本题也不例外.
因为2Sn=anan+1,所以2Sn-1=an-1a(nn≥2),两式相减,得到2an=a(nan+1-an-1).因为an≠0,所以an+1-an-1=2.所以{a2k-1},{a2k}都是公差为2的等差数列.
此时学生易给出错误答案:
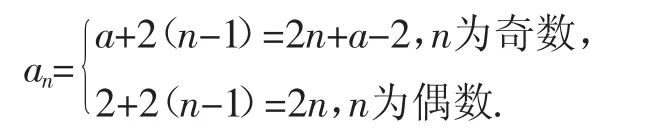
原因是机械地套用了等差数列通项公式,错误地认为奇数项与偶数项的项数均为n.
为了充分认识错误的原因,我们可列举数列的有限项,当n为奇数时,如取n=11,得a,2,a+2,4,a+4,6,a+6,8,a+8,10,a+10,则奇数项为a,a+2,a+4,a+6,a+8,a+10,共6项,并不是10,项数所以当n为奇数时,
同理,当n为偶数时,如取n=10,得a,2,a+2,4,a+4,6,a+6,8,a+8,10,则偶数项为2,4,6,8,10,共5项,项数为所以当n为偶数时
二、求和问题
奇数项与偶数项为不同类型的数列求和问题,应对奇数项与偶数项分别求和,再相加.求解中注意对奇数项数列与偶数项数列项数的准确把握.

三、求最值
数列的最值问题,以等差数列为例,若首项为正,且公差小于0,则前n项和有最大值,此时n的值可由an≥0求解.同理,若首项为负,且公差大于0,则前n项和有小值,此时n的值可由an<0求解.当然也可以利用前n项和的二次函数性质来求解.
第(3)问,方法1:因为2Sn=anan+1,由(2)知,an=
注意到所有奇数项构成的数列是一个单调递增的,所有偶数项构成的数列是一个单调递增的.
当n为偶数时,an>0,所以此时Sn>Sn-1,所以S15为最小值等价于S13≥S15,S15≤S17,所以a14+a15≤0,a16+a17≥0,所以14+15+a-1≤0,16+17+a-1≥0,解得-32≤a≤-28.
因为数列{an}是由整数组成的,所以a∈{-32,-31,-30,-29,-28}.
又因为an≠0,所以对所有的奇数n,an=n+a-1≠0,所以a不能取偶数,所以a=-31,或a=-29.
方法2:因为S15为最小值,此时n为奇数,当n为奇数时,根据二次函数的性质知道,有,解得-32≤a≤-28.
因为数列{an}是由整数组成的,所以a∈{-32,-31,-30,-29,-28}.
又因为an≠0,所以对所有的奇数n,an=n+a-1≠0,所以a不能取偶数,所以a=-31,或a=-29.
经检验,此时Sn为最小值,所以a=-31,或a=-29.
变式探究:若数列{an}满足an+1+(-1)nan=2n-1,则数列{an}的前60项和为__________.
解析:本题是填空题,故可以采用归纳的方法来寻找解题规律,当然它也可以用迭代法来求解.
由题意可知,a2-a1=1,a3+a2=3,a4-a3=5,a5+a4=7,…,所以a3+a1=2,a4+a2=8,a7+a5=2,a8+a6=24,…,从第一项开始,依次取2个相邻奇数项的和等于2,从第二项开始,依次取2个相邻偶数项的和构成以8为首项,以16为公差的等差数列,所以
综上,解决奇数项与偶数项为不同数列问题的思想方法主要有分类讨论思想、整体思想和等价转化思想,具体求解中,通常需要利用列举、合情推理或迭代的方法来寻找相邻几项的规律,进而明确数列问题的本质.
——以影片《流浪地球》中美德影评为例

