探一题多解，究多题一解——2017年高考全国卷解几题解法探究

☉广西百色祈福高级中学 陆逢波

探一题多解，究多题一解
——2017年高考全国卷解几题解法探究

☉广西百色祈福高级中学 陆逢波

一题多解是指同一个问题沿着不同途径，运用不同的知识和方法去思考，以探求多种答案、寻找多种解法的思维方式.而多题一解则恰好相反，是针对不同的问题在解决问题的过程中用到了同样的方法的思维方式.高考试题是命题专家精心雕琢的经典“作品”，它源于教材，又高于教材，体现命题者的命题思路、难度和考试方向，是高考复习的最好训练素材.中学数学课堂教学中引导学生对高考真题进行一题多解、多题一解的探究活动，有利于激发学生学习兴趣；有利于培养学生的发散性思维和集中性思维、培养学生的数学核心素养；有利于加强学生对知识的理解、深化和方法的掌握，从而提高高考复习的效益.本文以2017年高考全国课标卷理科解析几何试题为例，探究一题多解及多题一解在高考中的应用，供读者参考.

一、一题多解探究

例1（2017年全国课标卷Ⅰ理科第10题）已知F为抛物线C：y2=4x的焦点，过F作两条互相垂直的直线l1，l2，直线l1与C交于A，B两点，直线l2与C交于D，E两点，则|AB|+|DE|的最小值为（ ）.

（A）16 （B）14 （C）12 （D）10

分析1：由抛物线定义知，|AB|+|DE|=x1+x2+x3+x4+2p，再用“基本不等式”求最值.

解法1：设直线l1方程为y=k1（x-1），

同理，直线l2与抛物线的交点满足

当且仅当k1=-k2=1（或-1）时，取得等号.

分析2：利用对称性，当A与D，B与E关于x轴对称时，|AB|+|DE|最小.

解法2：直线l1，l2互相垂直，l1与C交于A、B两点，l2与C交于D、E两点，要使|AB|+|DE|最小，则A与D，B与E关于x轴对称，设DE的斜率为1，直线l2的方程为y=x-1，联立方程组则y2-4y-4=0，y1+y2=4，y1y2=-4，

所以|AB|+|DE|的最小值为2|DE|=16.

分析3：利用参数法，把A、B的坐标用参数表示出来，用两点间距离公式表示|AB|、|DE|，再用“基本不等式”求最值.

解法3：设l1∶x=my+1代入直线方程得

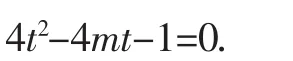
因为l1⊥l2，上式m用替换得

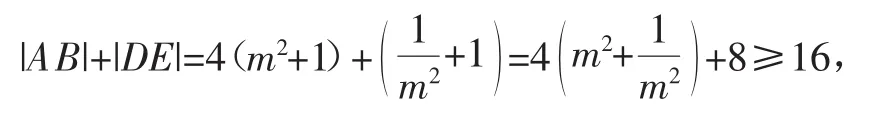
当且仅当m=±1时，取等号，故选A.

分析4：利用焦点弦长公式，快速求解.

解法4：设直线l1的倾斜角为θ，则l2的倾斜角为根据焦点弦长公式可得

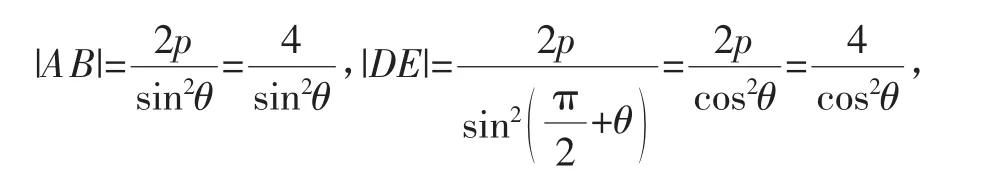
因为0＜sin22θ≤1，所以当θ=45°时，|AB|+|DE|的值最小，最小值为16.

例2（2017年全国卷Ⅲ理科第12题）在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上.若，则λ+μ的最大值为（ ）.

分析1：利用坐标法，把λ+μ用P点坐标表示，令-y+1，转化为圆心到直线距离小于半径，求出最值.

解法1：以B为原点，BC为x轴，BA为y轴建立直角坐标系，则A（0，1），B（0，0），D（2，1），P（x，y）.

分析2：利用坐标法，把λ+μ表示为三角函数，转化为三角问题，求出最值.

解法2：以A为原点，AB，AD所在直线分别为x轴，y轴建立直角坐标系，则A（0，0），B（1，0），C（1，2），D（0，2），可得直线BD的方程为2x+y-2=0.

二、多题一解探究

2017年全国高考课标卷3套理科试题中的三道解析几何大题，考查的内容、角度不尽相同，涉及直线、圆、椭圆相关的轨迹问题和直线过定点问题，但这3道题均可以统一用一种数学思想方法——参数法解答.

（1）求C的方程；

（2）设直线l不经过P2点且与C相交于A，B两点.若直线P2A与直线P2B的斜率的和为-1，证明：l过定点.

解：（1）由于两点关于y轴对称，所以由题设知C经过P3、P4两点，又P（11，1），不可能同时在椭圆上，因此可得椭圆经过点.代入椭圆方程得a=2，b=1，所以所求的椭圆方程为

（2）直线P2A与直线P2B的斜率分别为k1，k2，当直线l的斜率不存在时，设A，B的坐标分别为A（2cosθ，sinθ），B（2cosθ，-sinθ），

则直线l的方程为x=2，不合题意.

所以直线l的方程为y=k（x-2）-1.综合上述，直线过定点（2，-1）.

例4（2017年全国卷Ⅱ理科第20题）设O为坐标原点，动点M在椭圆上，过M作x轴的垂线，垂足为N，点P满足

（1） 求点P的轨迹方程；

所以点的轨迹方程x2+y2=2.

设椭圆左焦点F（-1，0），

所以过点P且垂直于OQ的直线l过C的左焦点F.

例5（2017年全国卷Ⅲ理科第20题）已知抛物线C：y2=2x，过点（2，0）的直线l交C于A，B两点，圆M是以线段AB为直径的圆.

（1）证明：坐标原点O在圆M上；

（2）设圆M过点P（4，-2），求直线l与圆M的方程.

将抛物线方程代入直线方程，得t2-mt-1=0.

根据韦达定理得t1+t2=m，t1t2=-1.

所以OA⊥OB，即原点O在圆M上.

（2）由于圆M过点P（4，-2），因此AP⊥BP.

设AP与BP的斜率分别为k1，k2，则

当m=1时，M（3，1），半径OM=%1 0，圆M的方程为

1.陆逢波.回归原点 以退为进——一道高考解几题的化归探究［J］.都市家教，2017（17）.

2.陆逢波.一道2017年高考试题的解法探究与拓展［J］.中学数学教学参考（下旬），2017（11）.