例谈高中解题的几种策略
☉江苏省沭阳高级中学 钱文奇
例谈高中解题的几种策略
☉江苏省沭阳高级中学 钱文奇
数学解题的教与学是数学教学的主要内容,数学解题能力是学生数学的核心能力,也是数学教学的着重点.在高中数学学习中,解题是高中数学学习的一个重要部分,也是很多学生困惑的地方.因为学生总感觉听懂了,题却解不出来.下面笔者结合多年的教学经历,谈谈高中解题的几种策略,以期抛砖引玉.
策略一、挖掘题目隐含条件
在求解数学问题的过程中,有些题目条件设置得很隐蔽,若不能很好挖掘使用,就很难正确解出结果.这就要求我们在解题中有意识地注意挖掘隐含条件,充分利用好所给的条件解题.
1.挖掘概念中的隐含条件
不少数学问题往往会在数学概念上设置障碍,若学生对概念理解不深刻,就很难观察到其中隐含的障碍.因此要解决好这类问题,必须对概念深入理解.
例1 已知l1:2x+my-2=0,l2:mx+2y-1=0,并且l1⊥l2,则m=______.
错解:有些同学认为l1⊥l2,则有k1·k2=-1,而由无解.
上述学生解错的原因就在于对线线垂直概念的不理解.结论“l1⊥l2,则k1·k2=-1”的前提的两条直线的斜率都存在.因此需要对斜率不存在的情况进行讨论.
正解:若m=0,显然l1⊥l2;若m≠0,则由l1⊥l2,得k1·k2=-1,而由矛盾,m不存在.于是m=0.
2.挖掘解题思维中的隐含条件
有的问题若按照常规思路来解决,则往往过程繁杂,无法解出.这时就需要转换思维,充分利用条件,有效解决问题.
例2设集合A={(x,y)|x=n,y=an+b,n∈Z},B={(x,y)|x=m,y=3m2+15,m∈Z},C={(x,y)|x2+y2≤144},问是否存在实数a,b,使下列条件同时成立?(1)A∩B≠Ø;(2)(a,b)∈C.
错解:由条件(1)
在x∈Z时有解,消去y,得
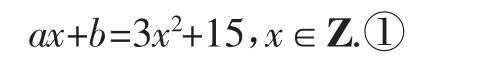
由条件(2)(a,b)∈C,得
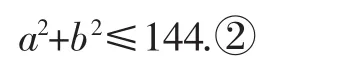
此题中常规思路就是将x视为变量,(a,b)视为常量,于是把①式视为关于x的一元二次方程,转化为关于x有整数解的问题,按照此思路,大多数同学束手无策,望而却步,无法正确解出结果.不妨转换思维角度,将(a,b)视为变量,把x视为常量,则可以将原问题转化为直线与圆面在整数范围内是否有公共点的问题.于是由d=得(x2-3)2≤0,从而只有显然与x∈Z矛盾,故满足条件的a,b不存在.
正解:由于(1)A∩B≠Ø;(2)(a,b)∈C同时成立,有解且a2+b2≤144,
即3x2-ax+15-b=0有解且a2+b2≤144,
则Δ=a2-12(15-b)=a2+12b-180≥0,且a2+b2≤144,
即180-12b≤a2≤144-b2,
故180-12b≤144-b2⇒b2-12b+36≤0,即(b-6)2≤0,
因此存在a,b满足条件.
策略二、跨越思维断层处障碍
在高中数学解题中,常常会有以下情景:遵循课本上所教讲的概念、公式、方法等,但是用着用着就会突然出现头脑里一片空白的情况.再去翻阅资料,会有一些提示,按照提示,问题就很容易解决,但是我们当时就是无法想出这个提示,即无法跨越这个思维的高度,也就是思维在这个点出现了断层.下面通过一道题谈谈如何跨越这种思维断层处的障碍.
例3设函数曲线y=(fx)在点(1,(f1))处的切线方程为y=e(x-1)+2.
(1)求a,b;
(2)证明:(fx)>1.
解:(1)函数(fx)的定义域为(
由题意得(f1)=2,f(′1)=e,故a=1,b=2.
设函数g(x)=xlnx,则g(′x)=1+lnx,所以当)时,g(′x)<0,
故h(x)在(0,1)上单调递增,在[1,+∞)上单调递减,从而h(x)在(0,+∞)上的最大值为
综上所述,当x>0时,g(x)>h(x),即(fx)>1.
学生拿到此题,都能想到用求导解决,但是很多学生在把(fx)>1转化为再变形成,再构造函数,求导数得令g(′x)=0,到这步后大多数学生无法解出,就是想不到将lnx与ex分离,即所谓出现了思维断层.在平时的教学中,应该要时刻警惕概念教学中的“滑过现象”,在解题中不断积累获取信息的能力,重视解题过程的教学,引导学生不断积累解题经验,加强教学反思,提高学生的解题能力.
策略三、注重解题后的反思与优化
解题过程中,学生较大限度地发挥了自身的数学水平,解题后老师及时了解学生的主要解题思路和解题阻滞点,在解法基础上设计好优化方案,挖掘出试题的本质特征,优化学生的解题方法,从而提升学生数学解题能力.
例4设函数(fx)=x|x-a|+b,a,b∈R.
(1)当a=2时,求函数(fx),x∈[1,2]的值域;
(2)对于给定的实数a(a≥2),存在实数b,对于任意实数x∈[1,2],都有不等式|(fx)|≤1恒成立,求实数a
2的取值范围.
针对第(2)问,学生作业中的解法如下:
解法1:由于,故由闭区间上二次函数的性质
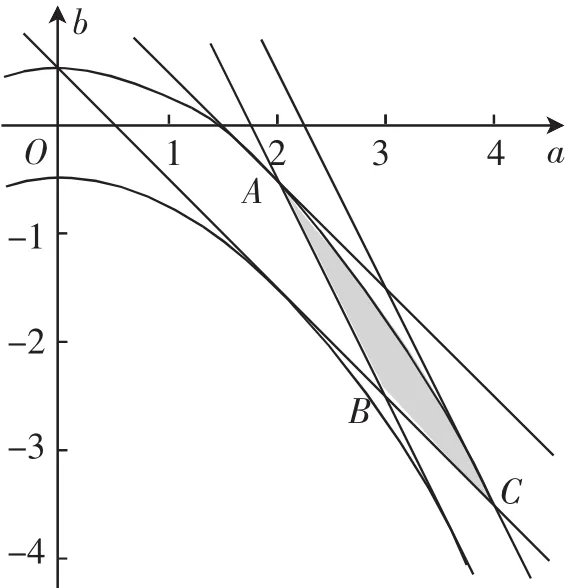
图1
解法2:由于,故命题“存在实数b对于任意实数x∈[1,2],都有不等式|(fx)恒成立”等价于“当
由于二次函数最值必在x=1,2,a处取到,据此展开2讨论
故a的取值范围为2≤a≤3或3<a≤4,即2≤a≤4.
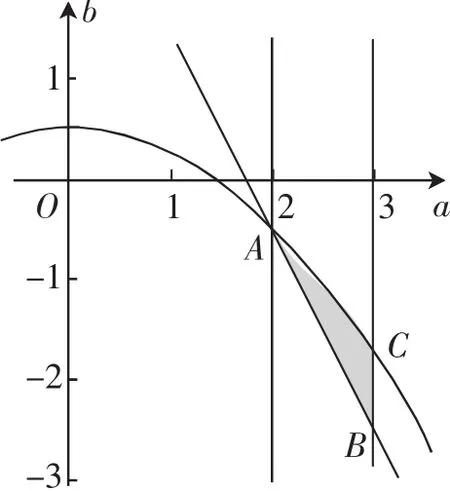
图2
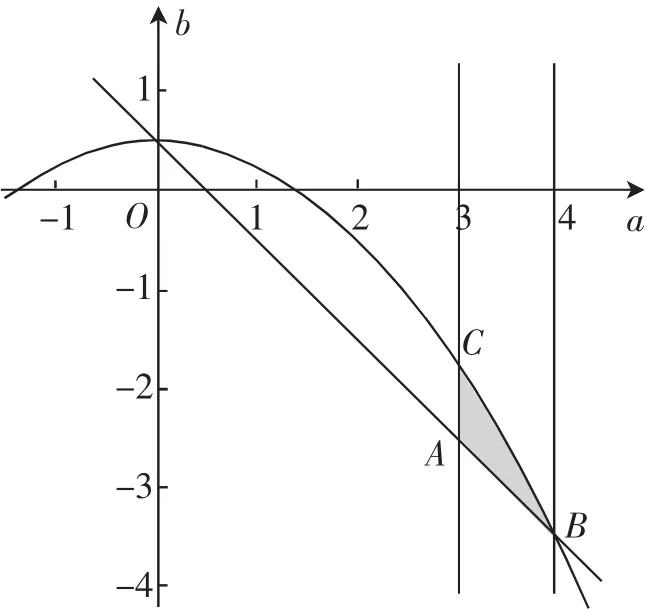
图3
这两种解法,可操作性强,但是运算量大,解题过程复杂,学生真正解出的很少.因此解题后可以引导学生对这两种解法进行优化.
解法1的优化:
同理利用不等式运算性质消去b,由④⑥可得2≤a≤6;由⑤⑥可得2≤a≤4,取三者交集得2≤a≤4.
故a的取值范围为2≤a≤4.
运用必要条件先缩小参数范围,减少了分类讨论的情况,大大简化了原解法.
由此可见,题后反思是学生所思和所想的自然延伸,跟随思维的发展进程,师生不断进行提炼和优化,这种由表及里、由粗到细,伸展不同方向的触角的解题分析方法,对提升学生的数学解题能力是大有裨益的.

