利用导数证明不等式的几种策略

☉江苏省常熟市浒浦高级中学 刘健玲

利用导数证明不等式的几种策略

☉江苏省常熟市浒浦高级中学 刘健玲

近年来，导数中的不等式证明问题在各地高考题中频频出现，这类问题往往难度较大，解题方法灵活多变，对学生的思维能力要求较高.如何利用导数证明不等式？笔者通过平时的教学实践，谈谈处理不等式证明的一些方法.

策略一、构造函数求最值来证明

近几年，函数、导数、不等式的综合问题是高考中的一个重点，也是一个难点和热点问题，学生往往对其束手无策.我们可以从不等式的结构特征出发，构造函数，通过求导研究，证明不等式.

例1 已知函数g（x）=lnx+ax2+bx，函数g（x）的图像在点（1，g（1））处的切线平行于x轴.

（1）用a表示b；

（2）试讨论函数g（x）的单调性；

（3）证明：对任意n∈N*，都有成立.

解：（1）b=-2a-1（.2）略.

（3）分析：由于定义域的特殊性，可以将此不等式右端视为一个数列｛an｝（an≥0，n∈N*）的前n项和，若将左端也视为一个正项数列｛bn｝的前n项和Sn，则只需证bn＞an（n∈N*），从而寻求出解题方向.

因为Sn=ln（n+1），所以当n≥2时，Sn-1=lnn，

当n=1时，b1=S1=ln2满足上式，

即证lnx＞-x2+3x-2，x＞1，

只需证lnx+x2-3x＞-2，x＞1.

由（2）知，当a=1时，函数g（x）=lnx+x2-3x在（1，+∞）上单调递增，

所以g（x）=lnx+x2-3x＞g（1）=-2，

所以lnx+x2-3x＞-2在x∈（1，+∞）上成立.

故问题得证.

证明：由（2）单调性的证明可知，当a=1时，函数g（x）=lnx+x2-3x在（1，+∞）上单调递增，

所以g（x）=lnx+x2-3x＞g（1）=-2，即lnx＞-x2+3x-2.

（1）若∀x∈［1，+∞），（fx）≤m（x-1）恒成立，求m的取值范围；

（2）分析：类似例1中不等式的证明思路，不妨将此不等式右端视为一个数列｛an｝（an≥0，n∈N*） 的前n项和，若将左端也视为一个正项数列｛bn｝的前n项和Sn，那么要证这个复杂的不等式，就只需证bn＜a（nn∈N*），从而寻求出解题方向.

要证原不等式成立，

令k=1，2，3，…，n，得如下n个不等式：

（1）若（fx）无极值点，求a的取值范围；

解：（1）（2）略.

（3）分析：类似上两个例题中不等式的证明思路，不妨将此不等式左端视为一个数列｛an｝（an≥0，n∈N*）的前n项和，若将右端也视为一个正项数列｛bn｝的前n项和Sn，那么要证这个复杂的不等式，就只需证an＞b（nn∈N*），从而寻求出解题方向.

要证原不等式成立，

观察（*）式，左边含有2n与2n+1，考虑到

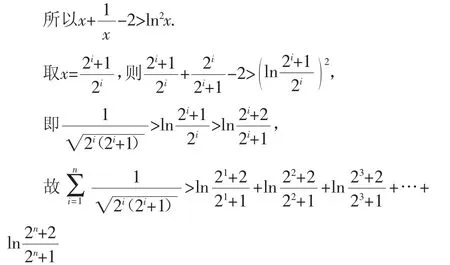
故结论成立.

构造函数证明不等式，要构造可导函数，利用导数得到函数的性质，再利用性质得出不等关系.

策略二、利用导数结合恒成立的思想证明

（1）求a，b；

（2）证明：（fx）＞1.

解：（1）a=1，b=2（.过程略）

设函数g（x）=xlnx，则g（′x）=1+lnx，

故h（x）在（0，1）单调递增，在（1，+∞）单调递减，从而h（x）在（0，+∞）的最大值为即（当且仅当x=1时取等号）.

本题在证明（fx）＞1时，学生会想到直接求出（fx）的最小值，再证明（fx）min＞1，或构造函数F（x）=（fx）-1，再证明F（x）min＞0.但这些解法都无法求出导函数零点，进而促进我们思考是由于exlnx引起，故想到将其分离，转化成然后再加强为（fx）min＞g（x）max进行证明，从而得到上面的证法.

策略三、利用导数结合放缩法证明不等式

有些题型，即使对函数变形后仍然很难找到解题的突破口，有时就有必要利用放缩法对原函数进行放缩.

（1）求a，b的值；

解：（1）a=0，b=-1（.过程略）

（2）由基本不等式，当x＞0时，

令g（x）=（x+6）3-216（x+1），则当0＜x＜2时，g′（x）=3（x+6）2-216＜0，因此g（x）在（0，2）内是减函数.

又由g（0）=0，得g（x）＜0，所以h（′x）＜0，

因此h（x）在（0，2）内是减函数.

总之，导数是解决数学问题的有力工具，不等式也是高考中的重点和难点，两者结合起来可以使得问题的解决简单便捷.因此在平时的教学中要多总结，多反思，长期以往，必将收到良好的利益.