复合函数求导方法的探究与应用

☉湖北省宜昌市第一中学 郑璇玥

复合函数求导方法的探究与应用

☉湖北省宜昌市第一中学 郑璇玥

复合函数求导在导数的运算中扮演者重要的角色，在平常的学习中，求导并不意味着对初等函数的求导.但是能否对初等函数进行精确求解，决定着是否能对复合函数进行正确的求解.因为不论是在高等数学还是目前的高中数学中的复合函数求导，不仅有基本初等函数的四则运算，还包括基本初等函数的复合.所以复合函数的分解与求解步骤是学习的重点.

一、复合函数的认识

一般地，对于两个函数y=f（u）和u=g（x），如果通过变量u，y可以表示成x的函数，那么称这个函数为函数y=f（u）和u=g（x）的复合函数，记为y=f［g（x）］.其中x成为自变量，u为中间变量，y为因变量.不是任何函数都能复合成一个复合函数，只有当u=g（x）的值域含于y=f（u）的定义域时，二者才能合成一个复合函数.［1］

由此我们可以知道，复合函数运算的对象虽然是变量y关于变量x的函数关系，但是其实早已不是仅对x进行简单的运算，而是需要关系到含有x的中间变量的运算上.所以对复合函数中含有x的式子的理解显得尤为重要.

二、复合函数的求解

1.图式表示法

为了方便理解复合函数的求导方法，需要明确函数结构内部变量间的关系，在此可以先利用画图来帮助理解.“树形图”如图1所示.［2］

图1

从图中可以清晰的看到，自变量、因变量、中间变量的分工情况及函数的从属关系.出现在“树形图”中树枝末端的变量为自变量.如图1所示，树枝末端变量只有一个，那就是t，则t是自变量，z是t的一元函数.

2.复合函数的求导法则

相比高中课本中的求导法则，引入偏导数与微分的概念更加便于理解复合函数求导的步骤与方法.

如果函数u=φ（t），v=Φ（t）都在点t处可导，函数z=（fu，v）在对应点（u，v）具有连续的一阶偏导数，则复合函数z=［fφ（t），φ（t）］在点t可导，且

其中z=［fφ（t），Φ（t）］仅是t的一元函数，则这里的称为全导数.［3］

结合图1，可以看到z经过t的线路有两个，即路径”z—u—t”和路径”z—v—t”与等式①对应，即

三、复合函数求导中易出现的问题

由于对初等函数求导的基础知识掌握不牢固，经常会出现各种问题，在此对几种典型的错误进行归纳.

例1设求y′x.［4］

错解：

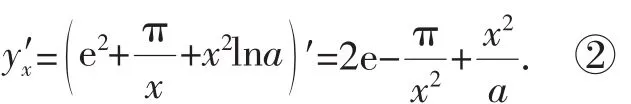
错解分析：本题的错误原因是基本初等函数掌握并不牢固，致使常数求导（d2）′=0，（lna）′=0错误的使用了指数、对数函数的求导公式.

正解：③

例2设，求y′x.［5］

错 解 ：

错题分析：复合函数的复合过程应为y=lgu，u=

正解

明显在错解中忽略了其中一步，致使求导出错.求解复合函数的导数，关键要弄清复合函数是由哪些基本初等函数或者简单函数复合而成，按照复合次序从外向内进行求导.所以注意复合函数的分层并且牢记“公式是基础，分层是关键”才是解题的关键.

四、复合函数的常用解题技巧

根据等式①，首先要清楚地分析复合函数的关系，找出要求导的复合函数是由哪几个初等函数组成的，然后再设置恰当的中间变量，把它分解成一些基本的初等函数的复合，最后由最外层开始，先使用法则，后使用导数的基本公式，由表及里一层一层求导，切记千万不可忘记里层的求导.根据以上的解题步骤，下面介绍一些求导的常用技巧.

1.幂指函数求解方法

例3求复合函数的导函数.［6］

解析：第一步，先对函数两边取对数，从而得到lny=

对数求导法则对一些幂函数，特别是乘积形式函数这类复杂的复合函数的求导显得十分便捷.在求解时对函数式两边取对数，然后对此对数式两边同时对x求导，但要注意在解题时，（fx）≠0时，而不是因为这一类复合函数求解十分烦琐，所以对这些式子需要进行化简、移项，确保得到最简洁、最精确的答案.

2.反序求导法复合函数的导数

反序求导法，其实是一种对复合函数从里到外一次求导的方法，它和上述的求导方法有相似性，但是其实质却有不同.反序求导法具有以下三个要点：第一，求导次序和求复合函数值的次序一致，方便上手，有助于对此方法的掌握和运用；第二，从里到外求导，避免了求导不彻底的问题；第三，形式上便于书写.

求导形式：通常由函数y=（fu），u=φ（x）构成的复合函数y=［fφ（x）］的导数时，是应用复合函数求导法则y′x=f′（uu）·φ（′x），从外到内求导；而反序求导则是y′x=φ（′x）·f′（uu），从里到外进行求导.下面进行举例说明：

例4求复合函数y=e-2x的导数.

解析：设y=eu，u=-2x，与反序求导法则相对应：y′x=φ（′x）·f′（uu），由内向外进行求导.u′=-2，y′=eu.

分析求导后进行数据整理后得到结果为y′=u′·（eu）′=-2e-2x.

五、总结

复合函数存在不同的种类，只有准确地把握函数内部结构的关系，才能有效地解决复合函数的求导问题.本文通过对复合函数的错题分析，同时也介绍相关的求解技巧.然而，复合函数的求解技巧远不止本文所列举的这些，由于篇幅有限，本文不再赘述.总之，熟练地掌握初等函数的求导法则，为求解复合函数打下牢固的基础，勤加练习才能减少出错的概率.

1.高一数学必修1［M］.北京：人民教育出版社，2015.

2.张晓妮.多元复合函数的求导方法研究［J］.科技教育，2016.

3.同济大学数学系编.高等数学下册［M］.北京：高等教育出版社，2013（4）.

4.张树林.一元复合函数求导法则及常见错误剖析［J］.科技视界，2015.

5.张月华.复合函数求导探析［J］.漯河职业技术学院学报，2011（2）.

6.毛涛.复合函数求导方法和技巧［D］.陕西理工学院，2015.