例谈不等式证明的几种策略

☉安徽省宁国市津河中学 汪庭斌

例谈不等式证明的几种策略

☉安徽省宁国市津河中学 汪庭斌

不等式有很多证明方法，笔者通过平时的教学实践，阐述证明不等式的几种方法，以期给初学者有所帮助，不对之处，欢迎指正.

策略一：待定系数法

有的题目往往很难凑出所要证明的式子，我们可以采取待定系数法来解决.

例1已知a，b∈R+，求证：

分析：尝试找到一个r，使得成立，故只需

依据已知条件可知原不等式等号成立时，a=b.

由上述分析可知：当a=1时，（fa）取得最小值0.

证明：

问题得证.

策略二：切线法

有的题目可以构造函数，通过求函数的切线解决不等式的证明.

例2 已知a，b∈R+，求证：

故可猜想y=Ax+B是（fx）在（1，（f1））处的切线方程.所以

策略三：割线法

例3 已知a，b，c∈R+，a+b+c=1，求证

分析：可知两点的割线方程是，故只需证+1在（0，1）上恒成立即可.

策略四：定积分解法

有类数列求和形式的不等式问题，通常是不等式与函数、数列、导数的结合，是高考的热点，对于此类不等式问题，常用的方法是数学归纳法和构造函数法，但是难度大，较难寻找解决问题的切入点.利用定积分的几何意义（曲边梯形的面积）来解决这类问题会收到意想不到的效果.

例4设函数（fx）=ln（1+x），g（x）=xf（′x），x≥0，其中f（′x）是（fx）的导函数.

（1）g（1x）=g（x），gn+（1x）=g（g（nx）），n∈N*，求g（nx）的表达式；

（2）若（fx）≥ag（x）恒成立，求实数a的取值范围；

（3）设n∈N*，比较g（1）+g（2）+…+g（n）与n-（fn）的大小，并加以证明.

分析：本题以函数为载体，导数为工具，具有综合性强、难度大、思维含金量高、区分度大等特点.下面来分析第（3）问.

思路一：构造函数

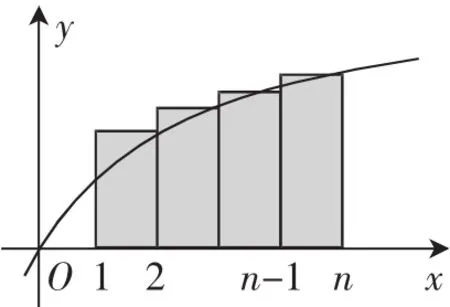
图1

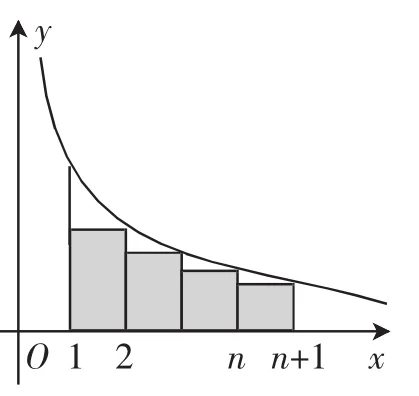
图2

思路二：因为需要比较的结果为，等价于构造函数并作图像如图2所示.因函数在［1，n+1］上是增函数，由函数图像可知，在区间［1，n+1］上的n个矩形的面积之和小于曲边梯形的面积，即

这类数列求和形式的不等式证明难度较大，往往令人望而生畏.要解决这类复杂问题的关键是建立在充分理解和掌握定积分有关知识的前提下，同时善于分析、善于联想、善于化归，才能达到以简驭繁、以形助数的解题效果.

策略五：放缩策略

放缩法是一种常用的证明技巧，主要用于研究与正整数有关的数学问题.猜想与递推是数列中常见的问题.而放缩法时常是数列证明问题中至关重要的一种策略，下面举例加以说明：

例5 已知数列｛an｝满足a1=1，an+1=3an+1.

分析：由题目我们很容易得出），构造辅助数列可以得出数列｛a｝的通项公式；n第（2）问中不等式左边的数列无法用公式进行求和，所以可以利用第（1）问中的结论对数列的通项进行适当的放缩.

证明：（1）由an+1=3an+1得

此外，对于这个问题的解答也可以通过递推放缩来完成，可以使证明过程更加简洁明了.

放缩法是证明问题的一种重要方法，特别是在证明数列不等式过程中，使用放缩法的关键是找到与需要证明的结论相关的关系，对于不同的问题可以适当变换策略.如改整体放缩为局部放缩，并兼顾整体特征来达到解决问题的目的.