高考试卷区分功能的评价方法研究

任子朝 关丹丹 佟威 陈昂

（教育部考试中心，北京 100084）

高考试卷区分功能的评价方法研究

任子朝 关丹丹 佟威 陈昂

（教育部考试中心，北京 100084）

高考是选拔性考试，强调对考生的精确区分，研究试卷的区分功能有助于科学评价试卷的区分效果，进而提高试卷的区分能力。试卷的区分功能可以用标准差的临界值、变异系数等统计学方法进行评价，也可参照试题区分度的评价方法，应用相关系数法和极端分组法进行评价。

高考改革；高考试卷；考试评价；标准差；区分度；变异系数

1 问题的提出

普通高等学校招生全国统一考试（以下简称“高考”）是合格的高中毕业生和具有同等学力的考生参加的选拔性考试[1]。高考属于常模参照测验，其分数更多地被用于确定考生在群体中的位置，以便高校根据考生成绩，由高到低择优录取。目前大多数省份用于录取的高考分数还是由语文、数学（文科或理科）、英语以及文科综合或理科综合的分数相加得到的，因此各科对考生的区分能力决定了高考总分的区分能力，研究一份试卷的区分功能进而提高高考的区分能力就显得非常必要。

2013年11月发布的《中共中央关于全面深化改革若干重大问题的决定》指出高考改革的方向，提出“探索全国统考减少科目、不分文理科、外语等科目社会化考试一年多考”[2]。新一轮高考综合改革，全国统考科目将只有语文、数学、外语三科，因此对这三科区分和选拔功能的要求更加突出。提高高考统考科目的区分功能，满足不同高校、不同专业的录取需求，是这三科的重要任务和巨大挑战。

新一轮高考综合改革的另一项改革措施是全国统一高考数学不再分文理科，所有考生使用相同的数学试卷。为此，数学科要重新构建学科考试的知识体系、能力框架、试卷结构和试题类型。因此，对数学试卷进行区分功能研究，将有助于提高文理合卷后的数学科的区分能力。本文以实行课程标准后数学科的实考数据为例，进行实证研究。

一般地，教育测量学研究试题的区分度，并作为评价试题质量的一个指标，对试卷则没有区分度的提法。本文提出试卷区分功能的概念，并参照试题区分度的评价方法，研究试卷区分功能的评价方法。

2 试卷区分功能的评价方法

对试卷区分功能的研究可以利用统计学的方法，同时借鉴试题区分度的研究方法进行深入研究。本文提出了应用试卷标准差的临界值、变异系数法、相关系数法和极端分组法评价试卷的区分功能。

2.1 标准差的临界值

标准差是考生分数离散程度的统计指标，标准差越大说明考生间的分数差异越大。一个服从正态分布的样本总体，当总体均值固定时，如果标准差愈小，则分布函数会变得愈尖，数据会愈集中，差异性也会愈小；如果标准差愈大，则分布函数会变得愈平，数据会愈分散，差异性也会愈大。

对于服从正态分布的样本总体而言，随机变量的绝对值在一个标准差范围内的概率可以达到68.3%，在两个标准差范围内的概率达到95.4%，在三个标准差范围内的概率达到99.7%。可见，对于一个样本群体，如果其服从正态分布，那么基本上所有的数据点都会集中在距离均值三个标准差的距离以内。

假设一份数学试卷的满分为150分，考生群体的分数符合正态分布，且均值为75分，那么能够基本覆盖全分数段的考生分数标准差临界值为25分。当符合正态分布的考生分数标准差大于或者等于25分时，考生分数能够有效覆盖［0,150］全量表范围，表明试卷有很强的区分能力。

根据表1，数学理科试卷的标准差平均值为27.83分，文科试卷的标准差平均值为28.51分，超过25分的临界值。结合试卷平均分可以看出，目前理科数学区分功能很好，文科数学虽然平均分偏低，但是由于标准差较大，高分段也有覆盖。

标准差的临界值是根据各科总分确定一个本学科标准差的合理阈值，由于高考不同学科各具特点，题型不同，所以每个学科还要根据本学科的实际情况确定标准差的合理范围。

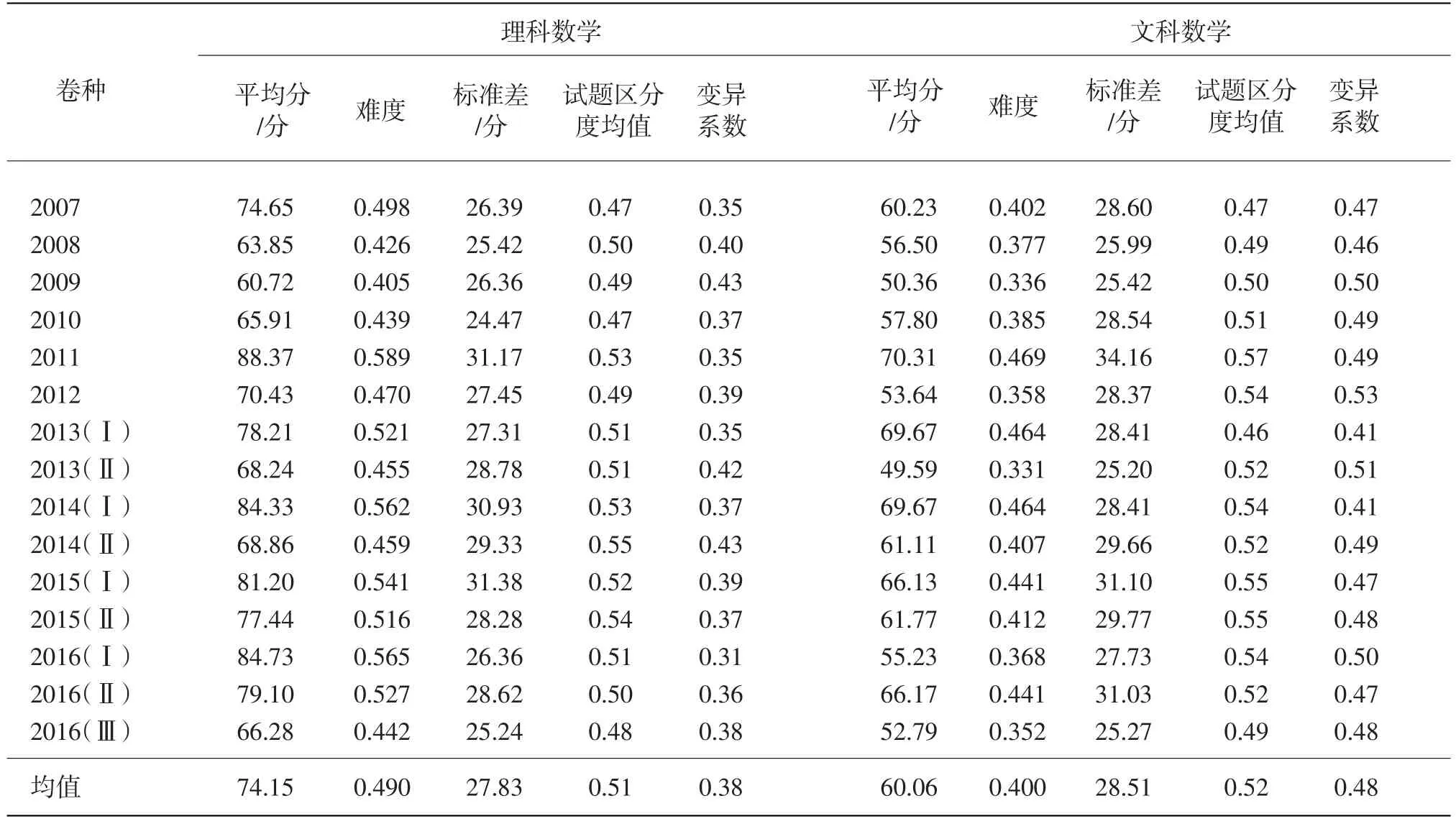
表1 2007—2016年高考数学（课标卷）统计数据

2.2 变异系数法

2.2.1 变异系数的概念和计算

标准差虽然能够比较两组数据离散程度的大小，但如果两组数据的测量尺度相差太大，如满分是150分和满分是300分的试卷，或者数据量纲不同，直接使用标准差来进行比较就不合适了。此时就应当消除测量尺度和量纲的影响引入变异系数，变异系数（Coefficient of Variation）是原始数据标准差与原始数据平均数的比值。变异系数没有量纲，可以更精确、更客观地比较两组数据离散程度的大小。变异系数并没有统一规定的阈值范围，可用于考生分数分散程度的相对比较，变异系数越大，分数分布越分散；变异系数越小，分数分布越集中。A.R.Feinstein主张实验监测数据的变异系数应该在5%～15%[3]。在本文中，借鉴变异系数的研究方法讨论考试数据的离散程度，这在考试数据分析方面还是创新，目前并没有固定的参考范围。

2.2.2 高考数学试卷的变异系数

在试卷难度与标准差和变异系数的关系方面，已有研究表明，一般对理科试卷而言，难度控制在0.5左右，标准差和变异系数达到比较好的平衡，即两者都比较高，考生分数分散程度较高；对文科试卷而言，难度在0.4左右，标准差和变异系数有较好的平衡[4]。试题是试卷的基本组成单位，试题的性能理所应当影响试卷的整体性能。本研究利用2007—2016年高考数学（课标卷）的实测数据，计算各卷中试题区分度（由单个试题得分与总分的相关系数计算得出）以及区分度的平均值，再根据标准差、平均分计算得到变异系数（见表1），以此探究试题区分度、试卷难度、标准差和变异系数之间的关系。

根据A.R.Feinstein提出的变异系数在5%～15%为合格的标准，从表1的结果可以看出，高考理科和文科数学试卷的变异系数均较高。这说明，整个试卷分数分布很均匀，并没有集中在某个分数区间。文科数学卷的变异系数整体上高于理科数学试卷。这说明，虽然文科数学试卷平均得分低于理科数学试卷，对于考生而言试题较难，但是，由于考生分数的变异系数较大，所以文科试卷依然保持着合理分数分布，特别是有利于对中低分数段考生的区分和甄别。

2.2.3 标准差、变异系数与试题区分度的关系

根据表1数据，通过散点图和回归分析来考察试卷标准差、变异系数与试题区分度的关系，见图1～图4。

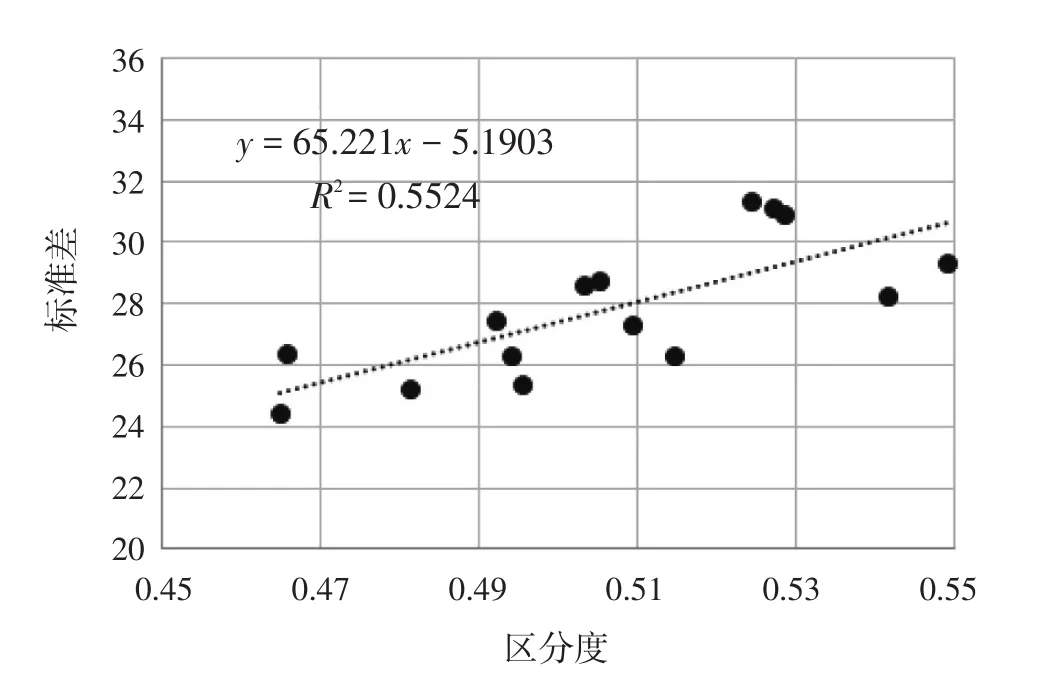
图1 高考理科数学试题区分度与标准差散点图

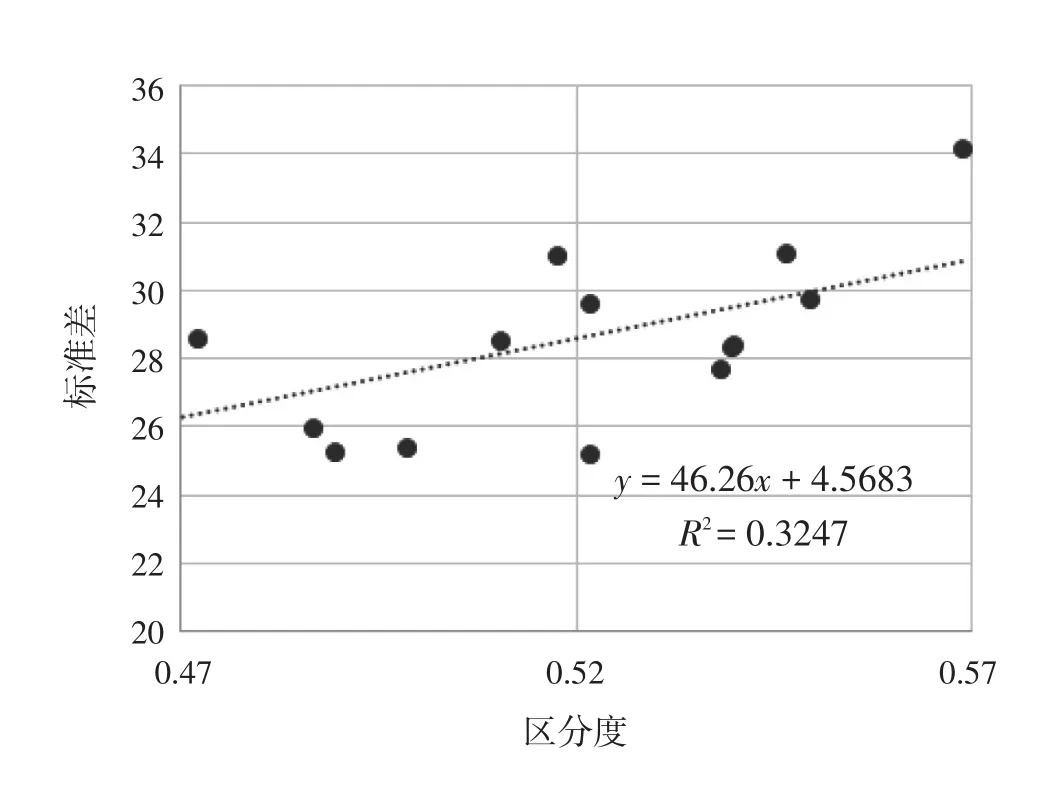
图2 高考文科数学试题区分度与标准差散点图

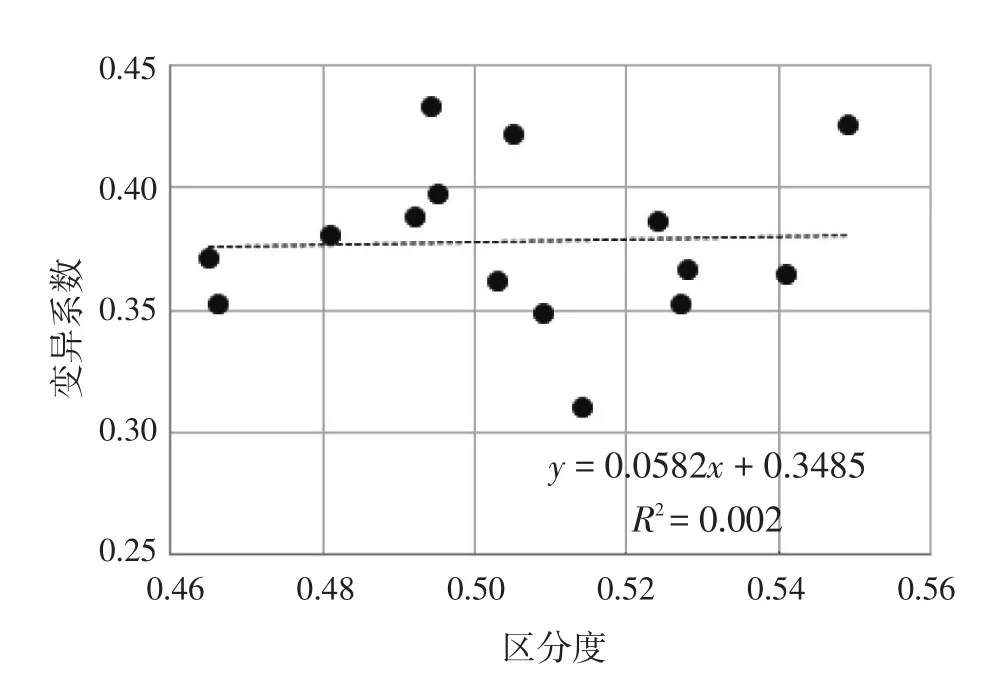
图3 高考理科数学试题区分度与变异系数散点图

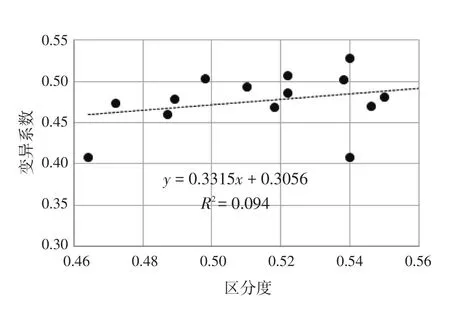
图4 高考文科数学试题区分度与变异系数散点图

从文理科数学试题区分度与标准差的散点图可以看到，两者具有比较明显的正相关关系，理科数学试题区分度均值对标准差的解释率甚至达到了55.24%，这说明提高单个试题的区分度对于提高试卷的区分功能有着显著的作用。

从文理科数学试题区分度与变异系数的散点图可以看出，高考文理科数学试题区分度与变异系数均无显著性相关。

综合试题区分度、试卷难度与标准差的关系来看，试题区分度对变异系数的影响作用被同样对标准差有较大影响的试卷难度所抵消，从而区分度对变异系数的影响程度减弱。这表明，要保持考生分数均值中等水平且有较高标准差，且能覆盖整个分数区间，需要从试卷难度、试题区分度等多个方面来综合考量。

2.3 相关系数法

试题区分度的一种计算方法就是计算题目与总分的相关系数。利用相关的思想，可以分析高考各科分数与总分的相关系数，以此评价各科试卷的区分功能。在分析过程中，考虑到各科目在总分中所占比重不同，除了对各科目得分与总分计算相关外，还对各科与不包括自身在内的其他科目分数和的相关进行了进一步分析。以H省和C市2016年高考试卷为例，计算数据见表2和表3。

从表2和表3的数据可以看出，在包括本学科在内统计相关系数时，理科综合、文科综合与总分的相关系数是最高的，而在单科中，数学与总分的相关系数是最高的。除去本学科后，理科中数学与其他科目分数和的相关系数最高，文科中文科综合与其他科目分数和的相关系数最高。其中的原因可能是文科数学的平均分比较低，影响了其在总分中的作用，还有可能是文科的思维方式和理科存在差别，理科偏重逻辑、推理的方法，而文科偏重辩证和历史的方法。

2.4 极端分组法

试题区分度的另一种计算方法就是高低分组法，即按考生在该题的得分把全体考生从高到低依次排列，然后从两极端确定前27%为高分组，后27%为低分组，再分别求这两组考生的得分率，设PH为高分组的得分率，PL为低分组的得分率，将其相减，得到该题的鉴别度指数D，D＝PH－PL。鉴别度指数的评价标准是：0.2～0.3为合格，0.3～0.4为良好，0.4以上为很好[5]。仿照这种计算方法，可以按考生在数学科的得分把全体考生从高到低依次排列，根据2016年H省高考数据，理科数学试卷高分组的得分率PH＝0.77，低分组的得分率PL＝0.14，得到D＝0.77-0.14＝0.63。同理，文科数学试卷的D值为0.61。按照D的评价标准，数学科文理两卷的区分功能都非常好。

在这个思想的基础上进一步发展，试卷的区分功能也可以使用分组法进行评价，分组的方法是根据高考录取批次划分相应的组别。以数学科为例，首先根据各省不同批次高考录取分数线，依据高考总分将考生分成本科一批、本科二批、高职专科、未被录取4个组别，分别计算每个组别高考数学的平均分、难度（即通过率或得分率）；相邻组别难度之差，即反映了数学对相邻两个批次考生的区分能力。若不同组别难度差别明显，则区分度良好；若不同组别难度差别很小，则区分度差。

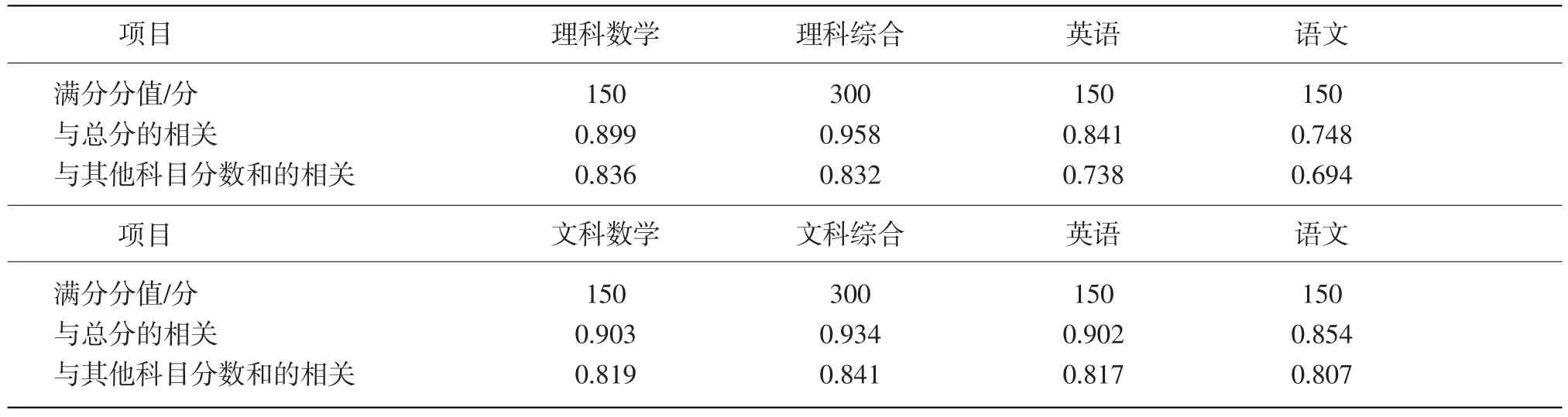
表2 2016年H省高考各科目分数相关计算结果

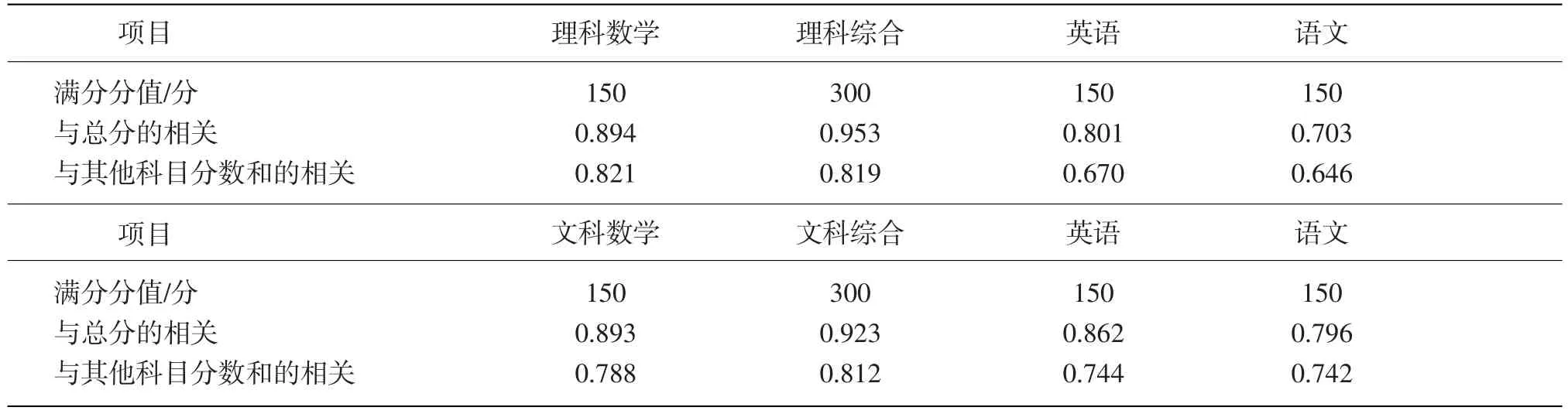
表3 2016年C市高考各科目分数相关计算结果

还以2016年H省高考数据为例，根据其公布的各批次分数线将考生分为4组，针对各组考生，分别计算各科成绩的平均分、难度等指标，见表4和表5。理科数学相邻两个批次通过率的差在0.15～0.25，不同批次考生的数学平均成绩至少相差22分。说明文理科试卷均能很好地区分各批次考生，数学科试卷具有良好的区分功能。

表4 2016年H省高考分批次理科数学试卷的统计数据

表5 2016年H省高考分批次文科数学试卷的统计数据

3 结语

从统计数据分析看，试题的难度和试题的区分度对试卷区分功能有显著影响。提高试题区分度则可以相应提高试卷的区分功能，试卷的难度与试卷的区分功能也有明显的正相关关系[4]。然而难度的提高可能会造成整卷偏难，对中学教学造成一定的影响，也可能影响对低分考生的区分能力，所以将试卷难度控制在何种水平还需要获取更微观的数据来进行具体的分析。综合当前的研究，适中的难度可以保障较高的试题区分度，同时试卷的区分功能较强，从而既可以有效区分考生，又有利于中学教学。

在评价试卷的区分功能时，可以基于统计数据采取多种方法进行分析。但同时，在考试中特别是在高考中，由于学科特点不同，采取的题型和试卷结构不同，所以试卷区分功能的评价方法不应该是单一的，应该结合学科特点综合选定。

提高试卷的区分功能首先要提高试卷的效度，即提高试卷考查的目的性，有效考查本学科的基础知识和重要能力。这是提高试卷区分功能的基础，只有在此基础上，试卷对考生的区分才具有实际意义。

[1]教育部考试中心.2017年普通高等学校招生全国统一考试大纲[M].北京:高等教育出版社,2016.

[2]中共中央关于全面深化改革若干重大问题的决定[M].北京:人民出版社,2013.

[3]FEINSTEIN A R.On chooosing a mean and other quantative indexes to describe the location and dispersion of univariate data[J].Clinical Pharmacology&Therapeutics,1980,27（1）.

[4]任子朝,佟威,陈昂.高考试卷难度与区分性能分析研究[J].数学通报,2017（1）:1-5.

[5]戴海崎,张锋,陈雪枫.心理与教育测量[M].广州:暨南大学出版社,2006:118.

Research on the Evaluation of the Discriminating Power of the College Entrance Examination

REN Zizhao,GUAN Dandan,TONG Wei,CHEN Ang
（National Education Examinations Authority,Beijing 100084,China）

As discriminating power is critical for the College Entrance Examination（CEE）to accurately distinguish students of different achievement levels,relevant research helps to scientifically evaluate and improve the discriminating power of the CEE.To that end,statistical indicators such as the critical value and the coefficient of variation can be used to evaluate the discriminating power of the CEE.Moreover,methods used to estimate the discriminating power of test items,such as the correlation coefficient and extreme groups,can also be used to calculate the discriminating power of the entire examination paper.

College Entrance Examination Reform;College Entrance Examination Paper;Evaluation of Examinations;Standard Deviation;Item/Test Discrimination;Coefficient of Variation

陈睿）

G405

A

1005-8427（2017）10-0007-6

10.19360/j.cnki.11-3303/g4.2017.10.002

本文系全国教育科学规划单位资助教育部规划课题“新高考改革背景下的高考质量评价研究”（编号：FBB160604）的阶段性研究成果。

任子朝（1961—），男，教育部考试中心，研究员；

关丹丹（1980—），女，教育部考试中心，副研究员；

佟 威（1984—），男，教育部考试中心，助理研究员；

陈 昂（1983—），男，教育部考试中心，助理研究员。