基于包络定位的谱峭度方法在滚动轴承故障诊断中的应用

姜锐红

(上海电机学院 机械学院，上海 201306)

基于包络定位的谱峭度方法在滚动轴承故障诊断中的应用

姜锐红

(上海电机学院 机械学院，上海 201306)

短时傅里叶变换(STFT)谱峭度(SK)(STFT-SK)方法将信号划分为任意频率中心与带宽组合的窄带，峭度最大的窄带信号可以精确定位滚动轴承故障信息的最优频带。然而，巨大的计算量限制了该方法的实际应用。根据滚动轴承故障调幅信号的频谱特性，提出包络定位频率中心的谱峭度方法(EL-SK)。先由滚动轴承故障信号频谱多次包络的极值确定窄带中心频率，再以一定步长变换频域窗宽，加窗截取频谱窄带；然后，对所截窄带进行傅里叶反变换后计算信号的峭度值，由最大峭度值确定最佳窄带的频率中心与宽度；最后，对最佳窄带信号做包络分析，即可提取轴承故障特征。利用STFT-SK和EL-SK两种方法对实测滚动轴承故障的诊断对比分析，验证了EL-SK方法的有效性与实用性。

短时傅里叶变换谱峭度； 包络定位谱峭度； 滚动轴承； 故障诊断

滚动轴承是各类旋转机械中使用最广泛的零部件之一。由于滚动轴承使用寿命离散性大[1]，定期更换的设备维护方式显然会降低对设备的有效利用度，同时也难确保设备的安全使用。因此，对滚动轴承状态的正确监测与诊断极其重要。共振解调是识别滚动轴承故障的有效方法[2-4]，而合理选择最优共振解调窄带信号是该方法的关键[5-8]。短时傅里叶变换(Shot-time Fourier Transform，STFT)谱峭度(Spectral Kurtosis，SK)方法(STFT-SK)以频率中心与带宽为变量，两参数的精细划分为自适应精确定位包含滚动轴承故障信息最强的最优窄带信号提供了可能途径[9-10]。然而，巨大的计算量限制了该方法的实际应用[11]。在STFT-SK方法的基础上，改进的Protrugram方法根据滚动轴承故障解调特征及故障频率值，预先给定窄带宽度，再以定步长移动窗函数，计算各窄带信号包络谱的峭度值，以峭度最大的窄带信号确定最佳窄带中心频率[12]。该方法虽然大大降低了计算量，但因人为给定带宽而丧失了带宽自适应性。本文根据滚动轴承故障调幅信号所表现出的频谱特性，提出一种自适应定位窄带的方法。通过对故障信号频谱多次包络，以包络极值确定窄带中心频率，再以定步长改变窗宽截取窄带，由窄带傅里叶反变换信号的峭度最大值确定最佳带宽。频率中心与带宽参数分两步自适应定位，降低了计算量，提高了实用性。

1 STFT-SK

STFT是将SK理论联系到实际应用中的有效途径[9-10]。假设连续信号x(t)的离散采样为x(n)，采样周期为1。给定窗宽为Nw的分析窗w(n)以步长P移动，则信号x(n)的STFT为

(1)

式中，f为频率变量；e-j2πnf为傅里叶变换因子；m为窗函数移动数；Xw(mP,f)的偶阶经验谱为

(2)

文献[9]中以Wold-Cramér分解条件非平稳过程定义并解释了SK，将条件非平稳过程的SK定义为能量归一化4阶谱累积量，即

(3)

式中，S4X(f)和S2X(f)分别为窄带信号频谱的4阶与2阶瞬时矩，在STFT与SK之间搭起了桥梁。

式(3)是一种时频估计，其中，Xw(kP,f)是信号x(n)以f为频率中心的一定带宽内滤波得到的复解调[9]。因此，基于STFT的SK是对Xw(kP,f)包络的能量时间分布测量。由于SK受所加窗宽的影响，最佳频带的确定需要对所有可能的窗宽作STFT计算，最终得到的三维Kurtogram是以Nw和f为二元变量的函数[10]。完成这个过程，对于长度为N的信号需要[N3/(2P)]lbN次复数乘法运算加上(N3/P)lbN次复数加法运算量。如此庞大的计算量使得STFT-SK的实用性受到限制。

2 EL-SK方法

2.1 EL-SK定义

Wold-Cramér分解实际上是滤波器组分解[9]，条件非平稳过程或信号x(t)可以视为经一系列无限窄的频带滤波结果之和。通过对信号频域的加窗傅里叶反变换可以实现窄带滤波。若信号x(t)的傅里叶变换为

(4)

则对应的窄带时域信号为

xw(t)=IFFT(X(f)wNw)=

(5)

式中，wNw为截断频谱所加的窗函数；窗函数宽度Nw为变量；IFFT为傅里叶反变换运算符。于是，窄带信号的偶阶瞬时矩为

(6)

将式(6)代入式(3)得到SK的另一种定义形式，为

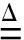
(7)

2.2 滚动轴承故障的调幅模型

轴承早期故障响应可视为弹簧-质量-阻尼单自由度系统[13]，轴承系统的加速度频响为

(8)

式中，fC为轴承系统的共振频率；F0为输入的外力幅值；k为轴承系统刚度；ζ为阻尼系数。

轴承故障信号可视为一系列这样的调幅信号迭加而成。结合滚动轴承故障冲击发生时刻具有因滑动引起的随机不确定性，以及幅值调制因素，滚动轴承振动信号模型为[13]

x(t)=A(t)·

(9)

式中，A(t)为调制函数；T为故障冲击发生的周期；IFFT(Xa(f))为冲击频响经傅里叶反变换的时域波；U(t-(kT+ΔT))为冲击时刻的阶跃函数；ΔT为故障冲击时刻的随机波动。

2.3 中心频率定位

离散信号x(n)的傅里叶变换为

(10)

对于调幅信号，有

(11)

式中，fb为调制频率；fS为采样频率；m为调制度；A0为信号振动幅值；θ0为载波的初始相位；θm为调制波的初始相位。

将式(11)代入式(10)，得

XAM(f)=A0[δ(f+fC)e-jθ0+δ(f-fC)ejθ0]+

δ(f-fC-fb)ejθm]ejθ0

(12)

由式(12)可知，载波频率幅值A0是边带频率幅值mA0/2的2倍。通常，m<1[13]，调幅信号的频谱有如下特点：以幅值较大的载波频率为中心，两侧对称分布有幅值较小的调制频率谱线。频谱包络线的轮廓包含了信号幅值变化趋势以及极值点位置等信息。因此，载波频率位置可通过信号频谱包络线的极值点确定。包络线为

Xen=fitsp(maxlo(abs(X(f))))

(13)

式中，abs(·)为绝对值算子；maxlo(·)为局部极大值算子；fitsp(·)为样条拟合算子。最终通过包络线的局部极值即可确定中心载波频率值，即

(14)

以如下包含3个载波频率的调幅仿真信号为例：

x(t)=[1+0.5sin(2πfbt)]sin(2πfC1t)+

(1+sin(2πfbt))sin(2πfC2t)+

(1+0.8sin(2πfbt))sin(2πfC3t)

其中，fb=90 Hz；3个载波频率为fC1=2.0 kHz，fC2=2.9 kHz，fC3=3.5 kHz。上述加性调幅信号的波形及其频谱如图1所示。在频谱图中，3个载波频率幅值明显大于边带频率幅值。频谱包络线的3个极大值点恰好为载波频率值。

2.4 窄带带宽确定

以下步骤可实现最佳窄带带宽的搜索：

(1) 以包络极值点对应的频率值为频带中心(载波频率)，在频率正、负半轴上对称加窗函数截取频谱，再对所截频带作傅里叶反变换，即得到相应的窄带信号为

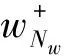
(15)

(a) 时域波

(b) 频谱包络

(2) 依据式(7)计算窄带信号的峭度为K(xw)=

(16)

(3) 由步骤(1)中确定的频率中心向左、右两侧逐点对称加大窗宽，重复步骤(1)、(2)，得到全部可能窗宽截取的窄带信号峭度。窗宽最大值为Nf/2，其中，Nf为正频率最大值(即采样频率的1/2)对应的点数。

(4) 由谱峭度值最大的窄带确定带宽。

因此，理论上，这种包络定位最优窄带的方法需要[N2/(2P)]lbN次复数乘法以及(N2/P)lbN次复数加法运算，其运算量为STFT-SK方法的1/N倍。

3 诊断实例

为检验EL-SK方法的有效性，将STFT-SK法与EL-SK方法分别应用于滚动轴承内圈实测故障的诊断，并将诊断结果进行对比分析。

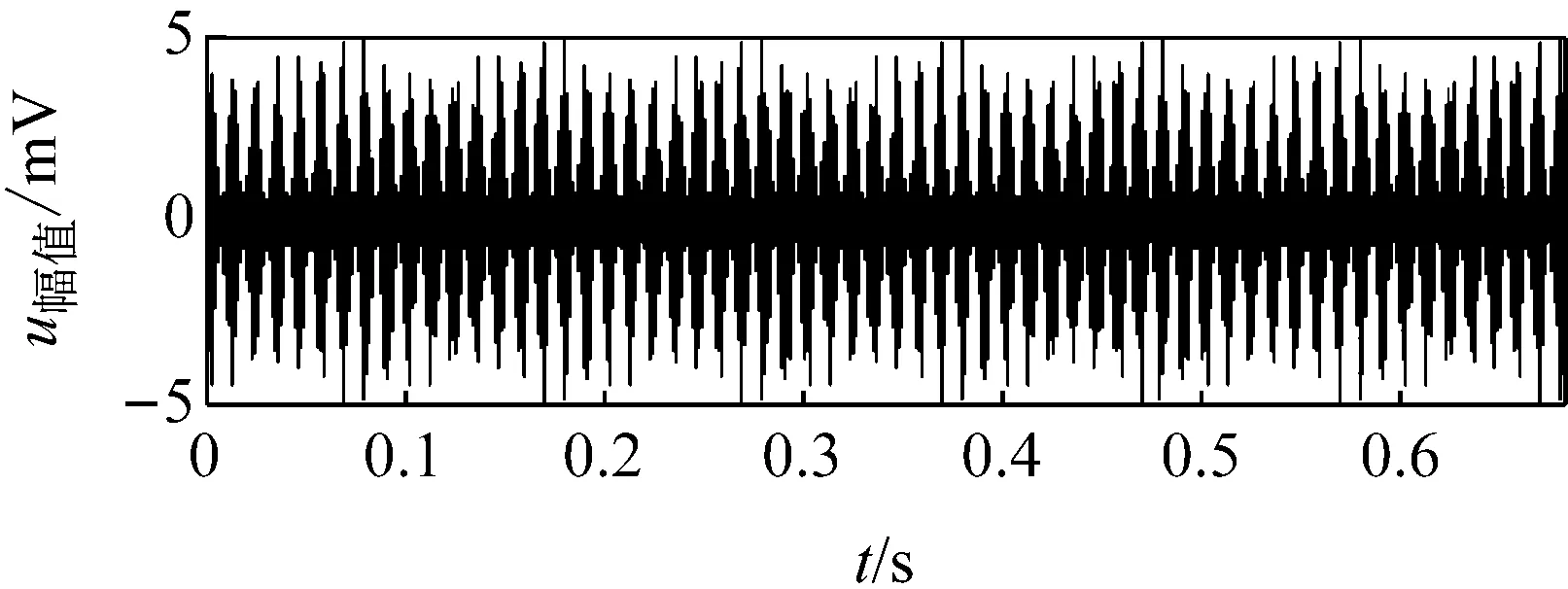
实测轴承故障信号来自美国凯斯西储大学轴承中心网站[14]。实验故障模拟采用6205-2RS JEM SKF型号轴承，故障信号在1 797 r/min的轴承转速工况下以12 kHz的采样频率测得。经计算得到转轴频率为29.95 Hz，保持架公转频率为11.9 Hz，内圈故障频率为162.2 Hz。

实测信号的时域波形及频谱如图2所示。由频谱图可以初步判断此轴承故障激发的共振频率不止一个，其中在2.5～3.0 kHz以及3.6 kHz附近分别为能量明显集中的区域，且两个区域的频率幅值大体呈现中间高、两边低的趋势，这恰是调幅信号的频谱特征，因此，可预测这是两个共振频率区。此外，还有几处区域能量较低，但频率幅值呈现中间高、两侧低的趋势，也是轴承系统固有频率可能存在的位置。具体哪个频带的信号最能够反映滚动轴承故障，还需要做进一步分析。

(a) 时域波

(b) 频谱

4.1 EL-SK方法诊断

实际的轴承故障信号载波成分以及调制信号均不一定是可完全单一确定的调制关系，信号的频谱往往较仿真信号复杂得多，需要对频谱做多次包络，方能够确定载波频率位置。如图3所示为实测内圈故障信号频谱经4次包络后的结果。

由图3可见，包络形状已基本勾勒出频谱幅值轮廓，可较好地将频谱划分为一些中心高、两侧较低的区域。图中，确定了7个幅值较大的极值点，表1给出了包络定位的各窄带信号峭度。其中，中心频率2 805.5 Hz确定的频带峭度值最大，因此，该窄带信号为目标最优频带。

图3 原始信号频谱及其4次包络

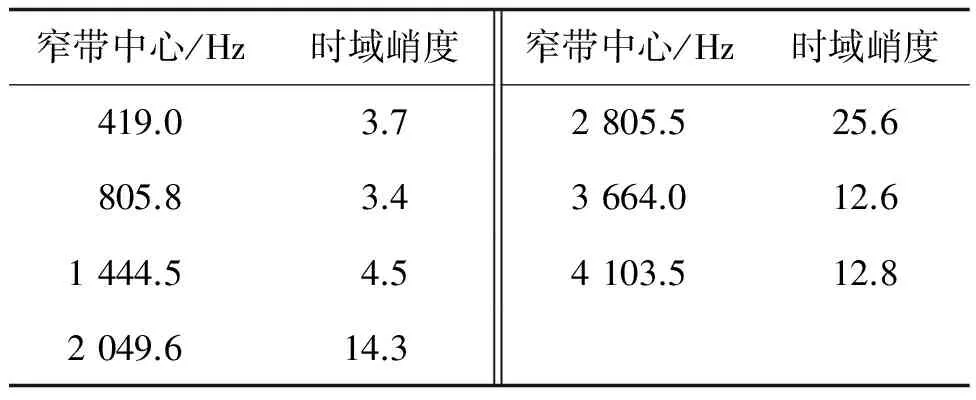
表1 包络定位的各窄带信号峭度

图4所示为最优窄带信号的时域波形及包络谱图。

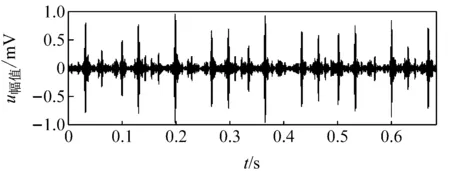
(a) 时域波

(b) 包络谱

由图4可见，时域波形图的冲击现象在该窄带中较原始信号表现得更加明显，故峭度值显著提高。在包络谱中，162.6 Hz的频率谱值与内圈故障特征频率162.2 Hz的非常接近，此窄带信号很好地诊断出轴承故障；此外，包络谱中29.3 Hz的谱值与11.72 Hz的谱值也明显突出，与轴承转轴频率29.95 Hz以及保持架公转频率11.9 Hz相吻合。其余较为突出的谱线分别为这3个特征频率的倍频及三者相互调制的结果，轴承内圈故障的所有特征在该窄带信号中得到全面、清晰的体现。

4.2 STFT-SK方法诊断

理论上，由全部可能窗宽得到的STFT-SK图能够精确定位包含滚动轴承故障信息最强的窄带。因此，本文对上述内圈故障信号做STFT-SK分析，以便检验EL-SK方法的实用性。

由于STFT-SK方法巨大的计算量令人难以忍受。此处仅对Nw=9～81(带宽范围为148.15～1333.33 Hz，该窗宽范围足以捕捉到上述内圈故障信号的特征),并以扩大P=8(带宽为131.7 Hz)的10个窗来计算，得到STFT-SK方法的谱峭度如图5所示。由图可见，Nw=9的谱峭度曲线由于带宽小于轴承故障特征频率，无法将故障信息完整包含在内，故峭度峰值并不明显；而Nw=17(带宽为279.8 Hz)的谱峭度线虽然有2处极大值，但与其余Nw下的峰值趋势不一致，尤其是在4 887 Hz处的极大值，其在其他窗宽峭度线上的峭度值几乎为极小值，这与Nw=17所对应的频带仍然较窄有关；Nw=25(带宽480 Hz)的峭度线与其余较大窗宽的峭度线趋势一致，且峰值最大。因此，以Nw=25的峭度线最大值对应的频率2 630.6 Hz为中心频率，分析该窄带信号。

图5 故障信号的STFT-SK

图6所示为得到最佳窄带信号及其包络谱。由图可见，该窄带包络谱图与图4的EL-SK最优窄带包络谱图基本一致，时域波形表现为明显的周期冲击，轴承的固有特征频率轴转频率与保持架公转频率，以及内圈故障特征频率均表现突出。

表2给出了STFT-SK方法和EL-SK方法诊断实验结果比较。实验中，计算时间对应的信号采样长度为2 048，使用TOSHIBA Satellite U800型笔记本电脑，CPU为Intel(R) Core(TM) i3-3217U 1.80 GHz，RAM为4.00 GB。由表可见，STFT-SK方法确定的窄带中心频率为2 631 Hz，与EL-SK方法定位的中心频率2 808.5 Hz有些偏差，但EL-SK方法确定的带宽523.0 Hz略高于STFT-SK方法确定的带宽 480 Hz，故可以认为这两种方法确定的最佳窄带基本吻合。此外，虽然STFT-SK方法诊断的故障特征频率幅值略高，而EL-SK方法诊断的故障特征频率幅值略低，但两种方法的诊断辨别度不相上下，最重要的是EL-SK方法计算所用时间仅为1.5 s，是STFT-SK方法用时的0.16%倍。因此，EL-SK方法对滚动轴承故障诊断具有一定的实用性。

(a) 时域波

(b) 包络谱

表2 STFT-SK方法和EL-SK方法诊断实验结果比较

4 结 语

本文针对STFT-SK方法同时盲识别频带中心与带宽的巨大计算量局限性，提出分步定位频率中心与窄带带宽的EL-SK方法。该方法理论计算量为STFT-SK方法的1/N倍。通过两种方法对滚动轴承内圈故障实测信号的诊断分析及性能对比，验证了EL-SK方法对滚动轴承故障诊断的有效性与实用性。文中，EL-SK方法所使用的窗函数均为矩形窗，故窗函数变化对诊断结果的影响需要进一步研究。另外，包络定位频率中心时，对信号频谱的包络次数确定如何实现自适应识别，也是今后需要完成的工作。

[1] WANG Dong，SUN Shilong，TSE P W. A general sequential Monte Carlo method based optimal wavelet filter: A Bayesian approach for extracting bearing fault features [J]. Mechanical Systems and Signal Processing,2015,52/53:293-308.

[2] JIA Feng， LEI Yaguo， SHAN Hongkai， et al. Early fault diagnosis of bearing using an improved spectral kurtosis by maximum correlated kurtosis deconvolution [J]. Sensors, 2015,15(11):29363-29377.

[3] AMIRAT Y, CHOQUEUSE V, BENBOUZID M. EEMD-based wind turbine bearing failure detection using the generator stator current homopolar component [J]. Mechanical Systems and Signal Processing, 2013, 41(1/2):667-678.

[4] 刘志川，唐力伟，曹立军．基于Kalman滤波和谱峭度的滚动轴承故障诊断 [J].轴承，2014(8):35-39.

[5] WANG Dong， TSUI K L， ZHOU Qiang. Novel Cause-Hermite integration based Baysian inference on optimal wavelet parameters for bearing fault diagnosis [J].Mechanical Systems and Signal Processing, 2016,72/73:80-91.

[6] 丁康，黄志东，林慧斌. 一种谱峭度和Morlet小波的滚动轴承微弱故障诊断方法 [J]. 振动工程学报，2014，27(1)：128-135.

[7] JIANG Hongkai, LI Chengliang, LI Huaxing. An improved EEMD with multiwavelet packet for rotating machinery multi-fault diagnosis [J].Mechanical Systems and Signal Processing, 2013, 36(2):225-239.

[8] ANTONI J. The spectral kurtosis: A useful tool for characterising non-stationary signals [J]. Mechanical Systems and Signal Processing, 2006, 20(2):282-307.

[9] ANTONI J. Fast computation of the kurtogram for the detection of transient faults [J]. Mechanical Systems and Signal Processing, 2007, 21(1): 108-124.

[10] ANTONI J, RANDALL R B. The spcetral kurtosis: Application to the vibratory surveillance and diagnostics of rotating machines [J]. Mechanical Systems and Signal Processing, 2006, 20(2): 308-331.

[11] SMITH W A，RANDALL R B. Rolling element bearing diagnostics using the Case Western Reserve University data: a benchmark study [J]. Mechanical Systems and Signal Processing, 2015,64(2) : 100-131.

[12] RANDALL R B, ANTONI J. Rolling element bearing diagnostics-A tutorial [J].Mechanical Systems and Signal Processing,2011,25(2): 485-520.

[13] 冯玉珉. 通信系统原理[M]. 北京：清华大学出版社, 2011:72-73.

[14] CASE WESTERN RESERVE UNIVERSITY BEARING DATA CENTER. Ball bearing test data for normal and faulty bearings [EB/OL].(2004-04-05)[2017-10-15]. http://www.eecs.case.edu/laboratory/bearing/download.htm.

Application of Spectral Kurtosis Method Based on Envelope Location to Fault Diagnosis of Rolling Bearings

JIANGRuihong

(School of Mechanical Engineering, Shanghai Dianji University, Shanghai 201306, China)

The spectral kurtosis method based on short-time Fourier transform (STFT-SK) divides a signal to a narrow band with combination of an arbitrary frequency center and a bandwidth. The narrowband signal with maximum kurtosis can accurately locate the optimal frequency band containing the strongest rolling bearing fault information. However, STFT-SK is impractical due to huge computation. According to the spectral characteristic of the rolling bearing fault, which is an amplitude modulation signal, a method of spectral kurtosis based on the envelope locating frequency center is proposed. The narrowband center frequency is confirmed by extrema of the multiple-envelope spectrum of the rolling bearing fault signal. The narrowband spectrum is then extracted by windows with fixed width step. A narrowband signal is obtained with inverse Fourier transform. Kurtosis of the narrowband signal is calculated, and the optimal bandwidth determined with the maximum kurtosis. The fault feature of the rolling bearing is extracted by an envelope spectrum analysis for the best narrowband signal. Availability and practicality of the EL-SK method are validated in actual fault diagnosis of rolling bearings with both the STFT-SK and EL-SK methods.

short-time Fourier transform-spectral kurtosis (STFT-SK); envelop locating-spectral kurtosis (EL-SK); rolling bearing; fault diagnosis

2017 -10 -30

国家自然科学基金面上项目资助(51575331)；国家自然科学青年基金项目资助(61603238)；上海高校青年教师培养计划项目资助(A1-5701-16-014-07)

姜锐红(1973-)，女，讲师，博士，主要研究方向为机电设备故障诊断，E-mail：jiangruihong2@163.com

2095 - 0020(2017)06 -0311 - 06

TH 133.33； TP 13

A