基于误差修正的极端学习机超短期风速预测

潘羿龙， 丁云飞

(上海电机学院 电气学院， 上海 201306)

基于误差修正的极端学习机超短期风速预测

潘羿龙， 丁云飞

(上海电机学院 电气学院， 上海 201306)

超短期风速预测对风电场功率预报系统的建立和运行至关重要。针对具有较大随机波动性的风速预测，研究了一种基于误差修正的极端学习机(ELM)超短期风速预测方法。利用ELM模型对风速进行初步预测，并利用由此得到的误差数据样本建立差分自回归滑动平均模型(ARIMA)，进行误差预测，最后使用预测误差对风速的初步预测值进行补正，从而求得最终预测值。仿真实验结果表明，该方法在风速超短期预测中的可行性及有效性。

风速预测； 预测误差补正； 极端学习机； 差分自回归滑动平均模型

随着风电装机容量的不断增加以及大规模的风电并网运行，风速的间歇性和随机性变化势必会对电力系统的安全运行带来严峻挑战[1]。因此，风速预测作为风力发电的基础，对电网的可靠运行具有举足轻重的意义，受到了越来越多的关注[2]。

从时间尺度上讲，风速的预测可分为长期、中期、短期以及超短期预测[3]。其中，长期预测是对一年或更长时间的预测，主要用于风电场选址与建设；中期预测为一周或数周内的风速预测，主要用来拟定风电机组检修计划；短期预测为48～72 h内的风速预测，主要用于电力调度部门的调度；超短期预测为4 h以内的风速预测，主要为风电机组的控制以及为电力实时调度系统提供参考。同时，超短期风速预测对电网并网运行也有重要作用，预测精度越高，实时调度系统做出的判断就越准确，对备用机组的选择也就越准确[4]。

对于风速的预测方法主要有时间序列法[5]、人工神经网络法[6]以及组合预测法[7]等，在预测效果上各有优、缺点。为提高风速的预测精度，各种组合预测方法受到了越来越多的关注，文献[8-10]中用时间序列分别与马尔科夫链、卡尔曼滤波、神经网络等方法组合进行风速预测。文献[11]中将最小二乘支持向量机(Least Squares Support Vector Machines,LS-SVM)与自回归滑动平均模型(Autoregressive Moving Average Model, ARMA)相结合，对风速进行短期预测。上述组合方法通过分摊单独预测的误差风险来减小大偏差对最终预测值的影响，但是，加权系数的强壮性一直是组合方法的瓶颈[12]。目前，更多学者关注的是通过改进算法本身来提高模型的预测精度。文献[13]中将LS-SVM与误差补正结合起来，提高了风速的预测精度。文献[14]中通过引入天气预报数值，利用BP神经网络与SVM相结合的方法对风速进行预测，获得了较好的效果。

极端学习机(Extreme Learning Machine，ELM)是近期发展起来的一种前馈神经网络方法，输入权值在训练过程中不需要多次调整，具有计算速度快、训练过程简单、抗干扰能力强等优点[15]，在实际操作中，有较高预测精度[16]。将ELM与时间序列方法组合起来可以在较短的时间内获得风速的预测值，为实时调度提供更好的帮助。

为了减少风速的预测误差，本文用ELM做初步预测时所获得的误差作为原始数据，导入差分自回归滑动平均模型(Autoregressive Integrated Moving Average Model,ARIMA)，获得误差预测值；并用该误差预测值对ELM的初步预测结果进行误差修正，以提高风速的预测精度。仿真实验结果表明，该方法在实际应用中具有一定的优势。

1 极端学习机(ELM)

ELM是一种前馈单隐层神经网络，图1所示为ELM网络结构。图中，J、K、L分别为输入层、隐含层、输出层的神经元个数，其中，j=1,2,…,J；k=1,2,…，K；l=1,2,…，L；ωjk为输入层第j个神经元与第k个隐含层神经元的权重；βkl为第k个隐含层神经元与第l个输出层的权重；X=[x1,x2,…,xJ] 为输入向量;Y=[y1,y2,…,yL]为输出向量,xJ、yL分别为输入、输出值。

图1 ELM网络结构

在确定了隐含层的激活函数f(x)后，ELM的训练输出向量为

T=[t1,t2,…,ti,…,tn]L×n,i∈L

其中，n为数据维数；ti为训练输出，

(1)

式中,ψk=[ωj1,ωj2,…,ωjK]为第j个输入神经元与隐含层的权值向量；bk为第k个隐含层的偏置;f(ψk,bk,xj)为第k个隐含层神经元输出，f(ψk,bk,xj)=f(ψkxj+bk)，激活函数可选择sigmoid或sine函数。

若ELM能以零误差逼近学习样本，则可以认为存在βk=[β1l,β2l,…,βKl]、ψk、bk，使

(2)

成立。

将式(2)改写成矩阵形式，

Hβ=Y

(3)

式中，H为隐含层输出矩阵；β为权值矩阵；Y为输出矩阵。这样上述问题就变成了求输出权值的最小二乘解β问题[17]，即

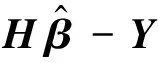
(4)

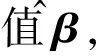
2 ARIMA

ARIMA又称为Box-Jenkins模型，是一种基于时间序列的预测模型，适用于短期和超短期预测，精度较高[4]。ARIMA模型先对数据进行d阶差分处理,使其平稳化，然后对平稳化序列建模,即得到ARMA,

(5)

在估计自回归系数、滑动平均系数时，最常用的是最小二乘法，可得到δg、θh；并根据赤池信息准则(Akaike Information Criterion，AIC)进行定阶，得到p、q[18]。

3 基于ARIMA修正的ELM预测模型

由于风速的随机、不稳定性，故在利用历史数据进行预测时，会产生误差。误差修正模型可以对当前的预测方法进行补充，结合预测方法的优势，可以更好地对风速进行预测。

3.1 基于误差修正的超短期风速预测流程

图2所示为基于误差修正的超短期风速预测流程图。具体步骤如下：① 先对风速的历史数据做归一化处理；② 将处理后的数据分为训练集D1、测试集D2和预测集D3，并用训练集D1对ELM训练，用确定好的ELM模型对测试集D2、预测集D3进行预测；③ 用预测集D1对ELM做训练，用测试集D2对ELM做测试，将获得的训练误差和测试误差作为误差数据；④ 判断序列是否平稳，若平稳，则使用ARMA模型，若不平稳，则使用ARIMA模型；⑤ 将初步预测值与误差预测值叠加获得最终风速预测值。

图2 超短期风速预测流程图

(1) 对原始数据进行归一化处理。远离零区域的数据会对学习速度造成影响，故在训练前要对数据进行归一化处理。本文将风速原始数据映射到[0,1]内，训练结束后再反映射回原数据空间，即

(6)

(2) ELM参数选取。当用大量的历史数据进行学习时，ELM可有效地提高预测模型的预测精度。与传统SVM相比，ELM在进行模型训练时还具有较快的运算速度。

图3所示为ELM参数选择流程图。

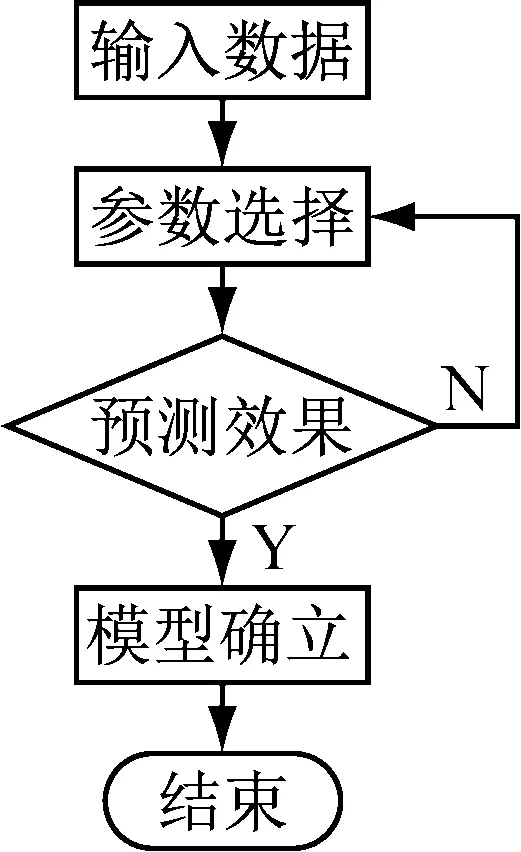
图3 ELM参数选择流程

在进行ELM训练时，以ELM输出误差与真实值之比作为评价标准判断ELM模型的好坏。ELM训练步骤如下：① 进行ELM初始化。本文选取sigmoid函数为激活函数，随机产生输入权值Г、隐含层偏置B，并根据实验确定隐含层神经元的个数，完成ELM网络初始化；② 根据误差率的大小作为评价标准来评价ELM初步预测结果的好坏，多次运行程序，选取其中较好的结果所对应的ELM参数作为模型参数；③ 应用确定好的ELM模型进行风速初步预测。

(3) 输入数据平稳性判别。 单位根检验由Dickey-Fuller于1979年提出，主要用来验证时间序列是否存在单位根，若数据小于显著性水平α，则认为不存在单位根，即数据平稳[19]。本文使用目前使用较多的判断方法——增广DF检验(Augmented Dickey-Fuller，ADF)[19]来进行输入数据的平稳性判别。

(4) 误差拟合预测。图4所示为误差数据预测图。具体过程如下：① 根据自相关、偏相关图估计p、q的大致取值；② 根据AIC准则选取最优p、q值；③ 建立ARIMA模型进行误差预测。

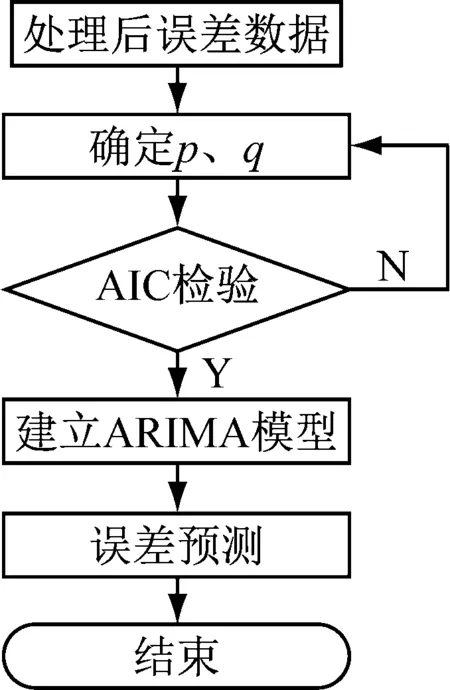
图4 误差数据预测流程

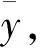
(7)

4 仿真结果与分析

为验证本文方法的可行性，对东北某电厂2007-04-07—2007-04-11采集的风速数据进行分析，采集高度为71 m，每10 min记录一次，共计720个数据；其中，前576个数据用于数据训练，中间132个数据用于测试，后面12个数据用于最终预测。

图5为720个风速数据的折线图。图中，n为数据个数。其中，最大风速值vmax=14.02 m/s，最小风速值vmin=0.35 m/s，可见，风速波动较大。

图5 风速历史数据图

选取前576个数据作为训练集D1，利用ELM模型进行数据训练；将中间132个数据作为测试集D2，进行风速预测，图6所示为预测值与实际值。

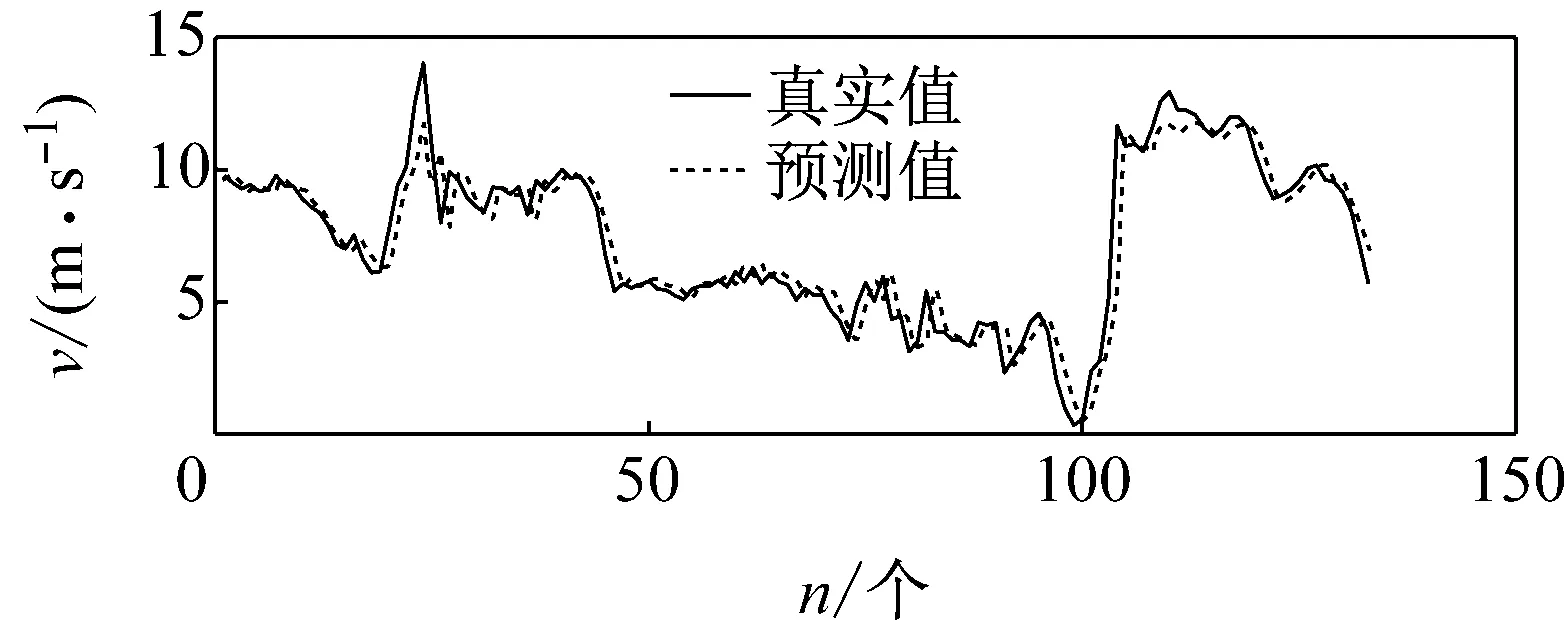
图6 测试集预测值与实际值

由图可见，当风速v出现明显的起伏波动时，风速的预测误差也越大。

为进一步提高预测精度，本文采用误差修正方法，利用ADF对误差数据进行平稳性检验。得到如表1所示的1阶差分后的单位根检验结果。

表1 1阶差分后单位根检验结果

一般认为当ADF检验所得到的t检验值<5%测试临界值的t检验值时，数据平稳。由表可见，经ADF检验的t检验值<1%测试临界值的t检验值，故认为1阶差分后的误差数据不存在单位根，此时序列是平稳的。

利用Eviews软件得到自相关和偏相关图如图7所示。图中，虚线内区域为置信区间。Autocorrelation为自相关图;Partial Correlation为偏相关图;AC为自相关系数;PAC为偏相关系数;Q-Stat为Q统计量，用于检验白噪声;Prob为小于显著性水平的概率。由图可见，自相关部分，第7个数据已经明显收束到区间内；而偏相关部分，第2个数据已经明显收缩在区间内。故依据定阶规则，p、q的取值应为 [0-7]内的整数。

图7 自相关与偏相关图

针对(p，q)的不同组合，采用最小二乘法对ARMA(p，q)模型中的未知参数进行估计；然后利用AIC准则,选择最小的那一组作为ARMA的p，q阶数。本文最终选取ARIMA(4，1，2)模型对初步误差进行预测。

利用ARIMA模型可得到误差预测结果与实际误差值的比较，如图8所示。

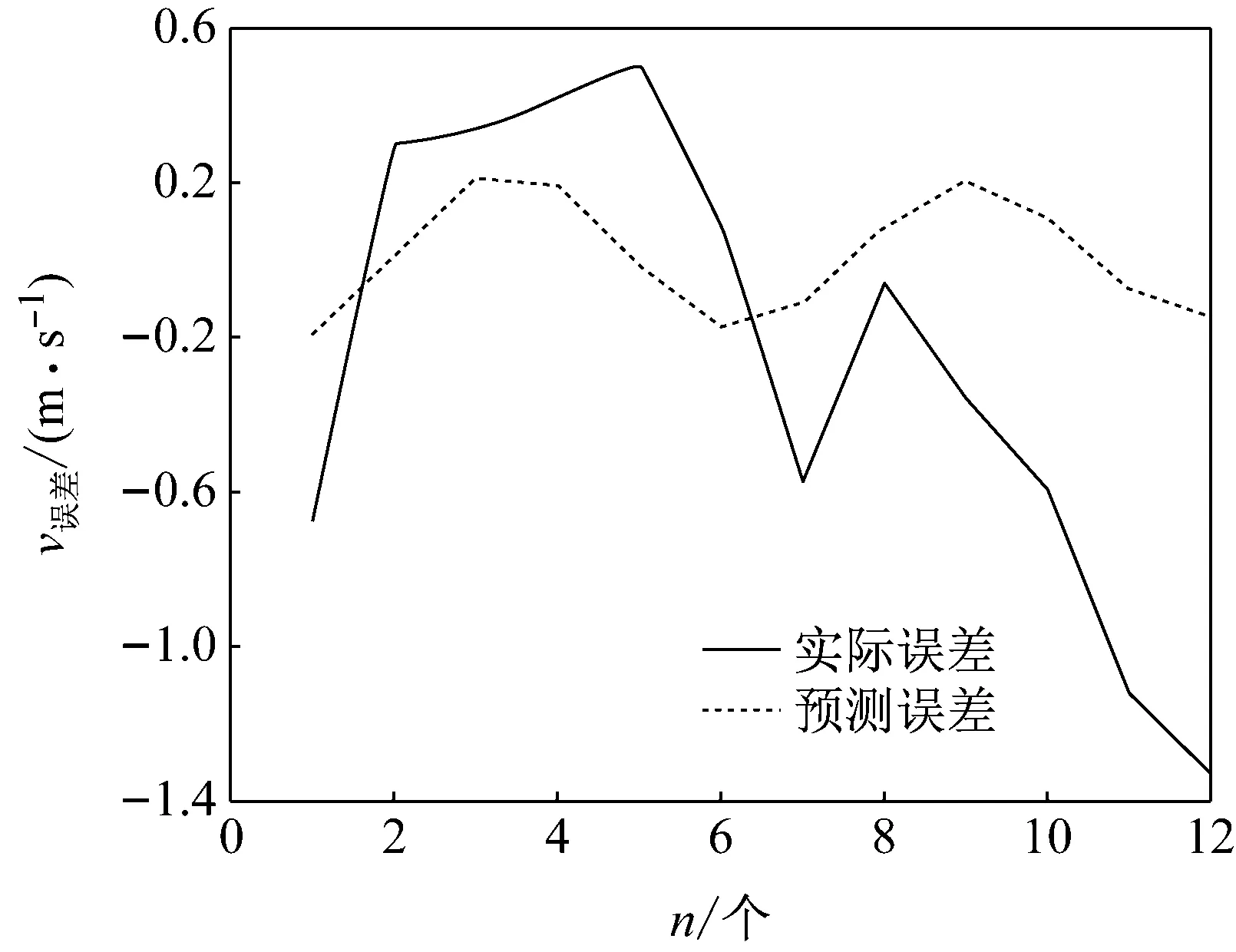
图8 ARIMA的误差预测值与实际误差值的比较

由图可见，随着预测步长的增加，误差的预测值与实际误差值的偏差加大。因此，ARIMA模型更适用于超短期和短期预测。故将本文方法用于超短期风速的预测，并与ELM预测值、实际值进行比较，图9所示为超短期预测结果。

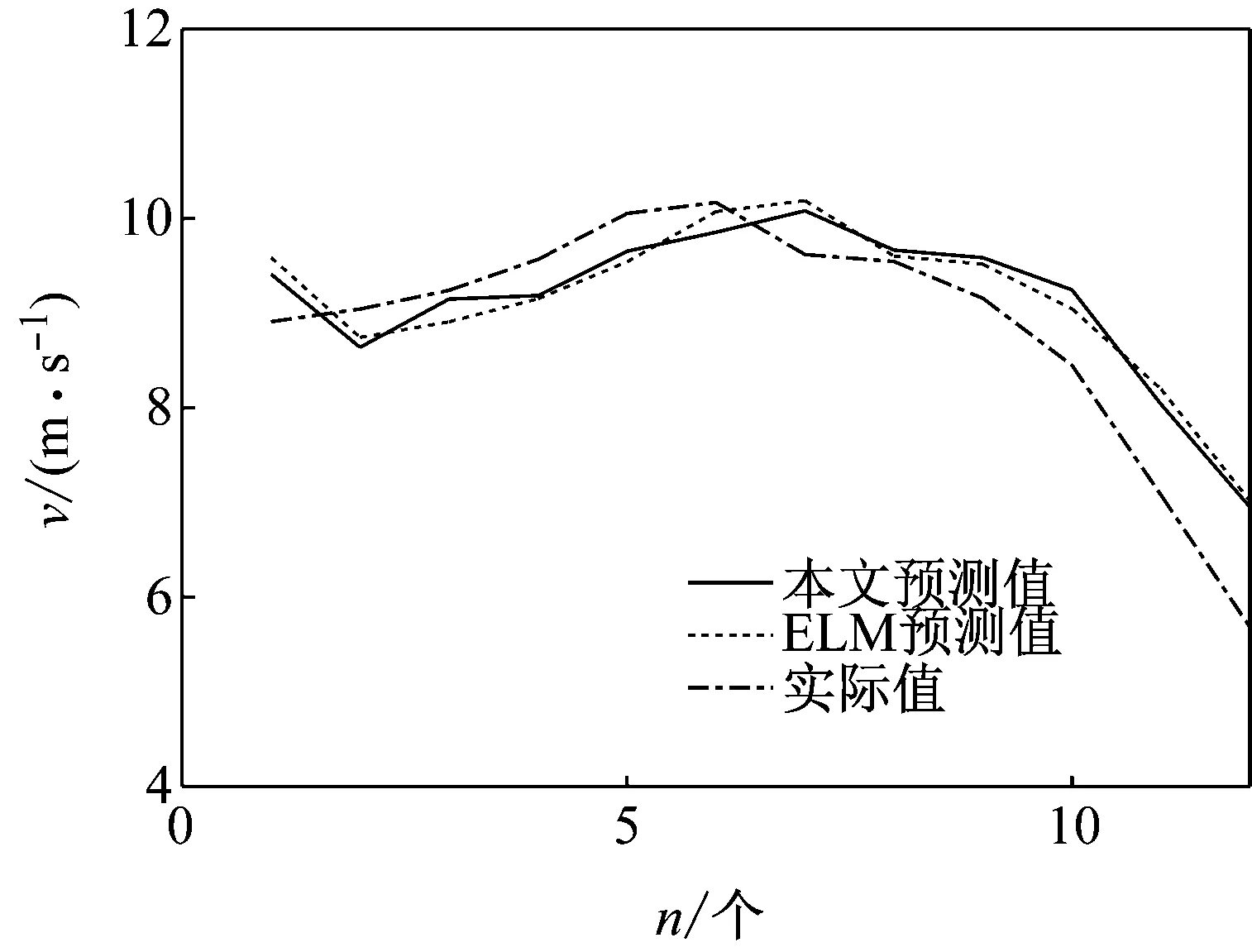
图9 最终预测图

由图可见，应用本文方法进行超短期风速预测，步长越短，预测效果越好。

为评价本文方法的预测精度，选取平均绝对百分比误差(Mean Absolute Percent Error，MAPE)、平均绝对误差(Mean Absolute Error，MAE)、均方误差(Mean Square Error,MSE)来对模型的预测结果的准确度进行评价，其中，

(8)

(9)

(10)

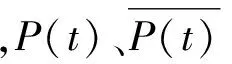
表2给出了本文方法与SVM、LS-SVM、ELM方法的实验结果评价。

表2 不同模型的风速预测用时与评价结果

由表可见，本文方法的误差率明显较LS-SVM和ELM方法低；与SVM 方法相比，除EMSE外，其他指标也明显低于SVM方法。可见，本文方法有效提高了预测的精度。同时，与SVM相比，本文方法运算速度快，且精度较高，SVM的EMSE值优于本文方法是由于随机确定的ELM参数不能很好地拟合预测数据中的突变点，这也是本文后续将要进行的研究；LS-SVM计算速度快，但精度较低。因此，本文方法在实际应用中具有一定的优势。

5 结 语

本文针对具有较大随机波动性的风速，提出了基于误差修正的风速超短期预测方法。利用ELM对风速进行初步预测，并取得预测误差；然后，对误差进行拟合与预测；最后，对风速初步预测值进行补正，从而求得最终预测值。仿真实验表明，本文所提出的对误差进行修正的风速超短期预测方法可以提高风速的预测精度，优于单独使用ELM前馈神经网络的预测值。本文所提出的方法也可以推广到负荷预测等领域，具有一定的泛化能力。

[1] 韩爽. 风电场功率短期预测方法研究 [D]. 北京：华北电力大学, 2008：绪论1-2.

[2] 杨秀媛，肖洋，陈树勇. 风电场风速和发电功率预测研究 [J]. 中国电机工程学报, 2005, 25(11): 1-5.

[3] 南晓强, 风电预测技术及其运行分析 [D]. 成都：西南交通大学， 2013:5.

[4] 丁藤，冯冬涵，林晓凡，等. 基于修正后ARIMA-GARCH模型的超短期风速预测 [J]. 电网技术, 2017，41(6): 1808-1814.

[5] 孙春顺，王耀南，李欣然. 小时风速的向量自回归模型及应用 [J]. 中国电机工程学报, 2008, 28(14): 112-117.

[6] KARINIOTAKIS G N, STAVRAKAKIS G S, NOGARET E F. Wind power forecasting using advanced neural networks models [J].IEEE Transactions on Energy Conversion,1996,11(4): 762-767.

[7] 张国强，张伯明. 基于组合预测的风电场风速及风电机功率预测 [J]. 电力系统自动化, 2009, 33(18): 92-95，109.

[8] PAPAEFTHYMIOU G, KLOCKL B. MCMC for wind power simulation [J]. IEEE Transactions on Energy Conversion, 2008，23(1): 234-240.

[9] 丁明，张立军，吴义纯. 基于时间序列分析的风电场风速预测模型 [J]. 电力自动化设备, 2005, 25(8): 32-34.

[10] 蔡凯，谭伦农，李春林，等. 时间序列与神经网络法相结合的短期风速预测 [J]. 电网技术, 2008, 32(8): 82-85，90.

[11] 田中大, 李树江，王艳文，等. 基于小波变换的风电场短期风速组合预测 [J]. 电工技术学报, 2015，30(9): 112-120.

[12] 薛禹胜，郁琛，赵俊华，等. 关于短期及超短期风电功率预测的评述[J]. 电力系统自动化, 2015,39(6): 141-150.

[13] ZHANG Y, WANG P, NI T, et al. Wind power prediction based on LS-SVM model with error correction [J]. Advances In Electrical and Computer Engineering, 2017, 17(1): 3-8.

[14] PENG Xiaosheng, DENG Diyuan, WEN Jinyu, et al. A very short term wind power forecasting approach based on numerical weather prediction and error correction method [C]//2016 China International Conference on Electricity Distribution. Xi’an, China: IEEE, 2016:1-5.

[15] 王新迎，韩敏. 基于极端学习机的多变量混沌时间序列预测 [J]. 物理学报, 2012,61(8): 97-105.

[16] 张学清，梁军，张熙，等. 基于样本熵和极端学习机的超短期风电功率组合预测模型 [J]. 中国电机工程学报, 2013, 33(25): 33-40.

[17] 王辉, 刘达, 王继龙. 基于谱聚类和优化极端学习机的超短期风速预测 [J]. 电网技术, 2015,39(5): 1307-1314.

[18] 蒋金良，林广明. 基于ARIMA模型的自动站风速预测 [J]. 控制理论与应用, 2008, 25(2): 374-376.

[19] 房林, 邹卫星. 多种单位根检验法的比较研究 [J]. 数量经济技术经济研究, 2007, 24(1): 151-160.

Ultra-short Term Wind Speed Prediction for Extreme Learning Machine Based on Error Correction

PANYilong,DINGYunfei

(School of Electrical Engineering, Shanghai Dianji University, Shanghai 201306, China)

Ultra-short term wind speed prediction is important for the establishment and operation of a wind power forecasting system. Aimed at wind speed with evident fluctuation property and randomness, an ultra-short-term wind speed prediction method for extreme learning machine (ELM) based on error correction is proposed. ELM are used to predict wind speed preliminarily. With the error as original data, using auto-regressive integrated moving average to predict the error. Finally, prediction error is used to correction the wind speed to forecast the wind speed. Simulation results show feasibility and effectiveness of the method in ultra-short term prediction of wind speed.

wind speed prediction; error correction; extreme learning machine (ELM); auto-regressive integrated moving average (ARIMA)

2017 -09 -10

国家自然科学基金项目资助(11302123)；上海市浦江人才计划资助(15PJ1402500)；上海市教育委员会科研创新项目资助(14YZ163)；上海市教育委员会和上海市教育发展基金会"晨光计划"资助(13CG63)

潘羿龙(1992-)，男，硕士生，主要研究方向为模式识别与智能系统，E-mail：363889821@qq.com

丁云飞(1976-)，女，教授，博士，主要研究方向为模式识别、智能控制、故障诊断、人工智能、数据挖掘，E-mail：dingyf@sdju.edu.cn

2095 - 0020(2017)06 -0342 - 06

TM 614； TP 183

A