基于自适应的月球着陆器悬停避障方法*

胡锦昌，张洪华，李毛毛

(1.北京控制工程研究所,北京 100190; 2.空间智能控制技术重点实验室,北京 100190)

基于自适应的月球着陆器悬停避障方法*

胡锦昌1,2，张洪华1,2，李毛毛1,2

(1.北京控制工程研究所,北京 100190; 2.空间智能控制技术重点实验室,北京 100190)

考虑质量和推力不确定性，月球着陆器在悬停避障时将难以快速稳定到设计高度.为解决此问题，提出一种基于自适应的高精度悬停避障方法，其核心是利用位置测量作为观测器的输入，对质量和推力不确定性进行快速估计和补偿.与基于PID的方案相比，该方案具有估计速度更快的优点，能够快速实现高精度的悬停避障控制.最后对所提方法给出仿真验证.

月球着陆; 悬停避障; 质量和推力不确定性;浸入与不变流形

0 引 言

在月球着陆器的悬停避障阶段，着陆器需要将自身位置控制到安全目标点的上方.在避障目标较远时，一般利用主发动机来提供避障所需的平动加速度，此时需要本体姿态机动来配合.此时控制目标为位置和姿态六个自由度，而输入为主发动机推力和三轴姿态控制力矩，可见此时避障问题实质上是一个四阶级联的欠驱动问题.对于此类欠驱动的着陆避障问题，在过去的几十年里已经得到了学者的大量研究.文献[1]针对速度不可测的情形设计了观测器及使得系统渐近稳定的控制器.文献[2]针对质量不确定的情形设计了自适应的控制器，在针对质量进行自适应辨识的同时，通过二阶滤波器来获得目标角速度和角加速度.文献[3]针对带液体晃动的月球着陆器，提出了一种基于无源性的位置和姿态控制器.文献[4]则设计了一种分层滑模控制器来稳定整个六自由度系统.文献[5]针对着陆器最终下降段设计了一种基于嵌套饱和函数的制导律.

在实际工程当中，难免会出现推力和质量的偏差.在设计避障控制律时，如果不考虑该不确定性的影响，那么将对竖直通道的控制产生重要影响.针对此问题，本文设计了不确定性的自适应律.实际控制律将利用自适应结果进行实时补偿.不同于文献[2]，本文利用位置而非速度作为不确定观测器的输入量，这样可以进一步降低估计结果的波动.

本文对推力和质量不确定性的影响进行了分析,在此基础上针对推力和质量不确定性设计了自适应控制器并进行了仿真验证.

1 问题描述与定义

为简化问题，考虑刚体形式的软着陆悬停避障问题.考虑到在悬停避障阶段，离月表比较接近，可以忽略月球自转的影响.设悬停避障开始时刻着陆器点为坐标系原点，竖直向上为z方向，x和y方向与z方向成右手坐标系.

基于以上假设，着陆器的平动和转动方程可写为：

(1)

(2)

(3)

(4)

其中：r∈R3表示着陆器相对于月表的位置；v∈R3表示着陆器相对于月球表面的速度；g:=[0 0 1.62] m/s2表示月表的重力加速度矢量；R∈R3×3为本体姿态相对于惯性空间的方向余弦矩阵；F∈R表示推力，m∈R表示质量；e3=(0 0 1)T表示本体系推力方向矢量；ω:=(ω1ω2ω3)∈R3表示卫星相对于惯性系的角速度，并且在本体系表达；u∈R3表示控制力矩；J∈R3×3为惯量阵；ω×定义如下：

假设1.相对月表的位置r可以通过导航系统得到.

假设2.设指令推力为Fcmd，实际推力F，实际推力与指令推力之间的关系为F=(1+x)Fcmd，其中x为偏差百分比.为简化问题，假设x为常值.

假设3.设实际质量为m，估计质量为m0，实际质量与估计质量之间的关系为m=(1+y)m0，其中y为偏差百分比.为简化问题，假设y为常值.

本文的控制目标为：基于假设1-3，设计推力F和力矩u的控制律，使得对一定范围的给定悬停初始状态，有：

r→rf，v→0，R→I3，ω→0

2 推力和质量不确定性的观测器设计

2.1 推力和质量不确定性的影响

设目标姿态对应的方向余弦阵为Rd，指令推力为Fcmd，则应该有：

(5)

其中制导律f(r,v)为位置和速度的函数.

假设不存在推力和质量不确定误差，那么将(5)代入(1)～(2)后得

(6)

(7)

由式(6)～(7)可知，只要设计制导律f(r,v)使得在姿态角误差收敛的同时，子系统(6)～(7)是渐近稳定的即可.

当存在推力和质量不确定性时，可得

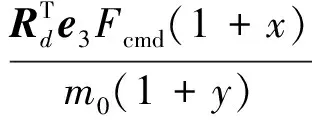
(8)

定义

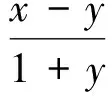
(9)

α为推力和质量不确定性的综合等参数.由此，式(8)可以简化为：

(10)

由式(10)可知，推力和质量不确定性的效果是两方面的.一方面，改变了制导律的增益，由于一般|α|<1，因此推力和质量不确定性一般不改变制导律的收敛性质；另一方面，推力和质量的不确定性在竖直方向产生了常值加速度.为了消除此常值加速度的影响，一般有两种方法：一种是在竖直通道引入积分项，即采用PID形式的制导律；另外一种是对不确定参数α进行辨识，并引入制导律的设计当中.考虑到积分过程一般比较缓慢，下面主要针对第二种思路进行控制器设计.

2.2 不确定性的观测器设计

基于式(9)，平动子系统动力学为

(11)

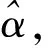
(12)

(13)

其中，ξ∈R和η∈R3为估计器的状态变量，Kr∈R3和kv∈R为增益系数矩阵.

设α和v的观测误差分别为：

(14)

(15)

对式(15)求导可得

(16)

可设

(17)

将式(17)代入式(16)可得：

(18)

对式(14)求导，可得：

(19)

设

(20)

将式(20)代入式(19)，可得

(21)

进一步求导，可得：

(22)

为证明观测误差方程(22)的收敛性，首先介绍引理1.

引理1.考虑如下所示的二阶系统：

(23)

其中，[x1x2]∈R×R为状态变量，kp,δkp>0，kd>0为反馈系数.则方程(23)全局渐近稳定的一个充分条件如下：

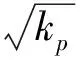
(24)

证明.针对方程(23)构造如下所示的Lyapunov函数：

(25)

易知V1>0.对V1求导并代入式(23)可得

(26)

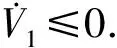
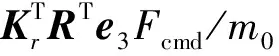
总结推力和质量不确定性的观测器如下：

(27)

(28)

(29)

3 控制器设计

3.1 制导律设计

基于对不确定性的估计结果，设计推力控制律为：

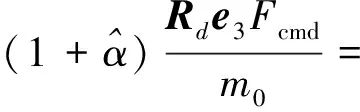
(30)

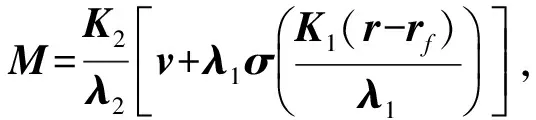
采用式(30)所示的控制律的优点主要包括3个方面：(1)通过嵌套饱和函数，可以在初始速度过大时优先进行减速过程；(2)可以控制各个分量的最大加速度大小，有效地限制本体的最大倾斜角，从而防止着陆器的翻倒并保证敏感器的视场；(3)通过限制式(30)的垂向分量，还可以防止发动机推力的奇异.

为表述方便，设：

(31)

基于式(30)，可以提取出目标推力为：

(32)

(33)

(34)

θ3d=0

(35)

由θd可计算得到目标四元数qd，从而可得到本体相对于目标姿态的误差四元数δq，具体过程可参考文献[2]，在此略.

下面给出平动子系统的收敛性证明.由此首先需要介绍引理2.

引理2[5]. 考虑如下所示的二阶系统：

(36)

其中,(x1,x2)∈R×R为状态变量，δ(t):R+→R为外界干扰，λ1,λ2,K1,K2为正常数.如果δ(t)→0，t→∞，并且各个参数满足如下所示的关系式：

K2λ1<λ2

(37)

那么状态(x1,x2)的最终收敛到零.

引理2的证明可参考文献[5]，具体过程略.

将(30)代入式(1)～(2)可得：

(38)

(39)

设

(40)

式(39)即可简化为式(36)的形式.

r→rf，v→0

证毕.

事实上，当δ(t)不趋于零但最终界很小时，仍然可以得到位置和速度最终有界的结果.由于篇幅所限，在此省略其证明.

3.2 姿态控制律设计

设计姿态跟踪控制律为：

u=-kpδqv-kvω

(41)

其中δqv为δq的矢量部分.

为理论上保证姿态跟踪系统的稳定，事实上式(41)还应考虑到对目标角速度和目标角加速度的前馈，其控制律形式如下：

(42)

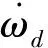
4 数值实例

月表重力加速度矢量为g=[0 0 -1.62] m/s2.选取着陆器的参数为：

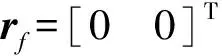
控制参数的选择为：Kr=[0.4 0.4 0.4]T，kv=1.6，σ(0)=38，η(0)=[150 183.5 -169]T，K1=[0.037 5 0.037 5 0.046 9]T,K2=[0.081 0.081 0.12]T,λ1=[0.49 0.49 0.49]T,λ2=[6 6 4]T.

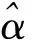
仿真结果如图1～7所示.图1与图2分别显示了位置和速度的控制结果，对于所设定的初始状态，在60s左右的时间即到达了安全着陆点上方.图3显示了本体相对于惯性系的三轴欧拉角(转序123)，三轴姿态最大在15°左右，能够保证着陆过程的姿态安全和正常的敏感器视场.图4显示了本体的角速度，尽管没有对目标姿态角和角速度进行前馈，姿态系统最终仍然是渐近稳定的.图5显示了主发动机推力方向与竖直方向的夹角，在避障过程中推力最大偏斜角不超过20°.图6显示了主发动机推力大小.图7给出了α的真实值与估计值的比对结果.由于质量消耗，α成不断增大的趋势，但是采用本文的方法仍然能够很好地跟踪时变的α.由图7可进一步看出，由于α的时变特性，α的辨识结果有微小的常偏，但是由图1和图2可见，此时仍然能够获得较好的悬停避障效果，表明本文的制导律有较好的鲁棒性.

图8显示了本文方法与采用积分消除推力和质量不确定的方法，及仅采用PD控制律的垂向控制结果的比较，其中积分系数已经过反复调试为一个最优值.由图可见，仅采用PD形式制导律时，垂向方向控制缓慢，并且具有较大的高度常值偏差；对于采用积分的方法来说，达到目标高度则需要大概120 s左右，比本文的方法慢了将近40 s的时间.

5 结 论

针对存在推力和质量不确定性的月球着陆器的悬停避障问题，本文提出了一种对不确定性进行快速辨识的方法.该方法利用浸入与不变流形的基本原理，以位置测量值作为观测器输入，可以实现不确定性辨识误差的快速收敛，同时可以减少辨识结果的波动.数值仿真表明，使用本文所提的方法可以快速实现竖直通道的高精度控制.后续将对喷气控制和存在姿控干扰力的情形进行进一步深入研究.

[1] ABDESSAMEUD A, TAYEBI A. Global trajectory tracking control of VTOL-UAVs without linear velocity measurements[J]. Automatica, 2010, 46(6): 1053-1059.

[2] HU J, ZHANG H. Immerion and invariance based command-filtered adaptive backstepping control of VTOL vehicles[J]. Automatica, 2013, 49(7): 2160-2167.

[3] 杜辉. 基于无源性的带液体晃动月球着陆器的姿态控制[J]. 空间控制技术与应用, 2011, 37(1): 50-54.

DU H. Passivity based attitude control for lunar lander with fuel sloshing[J]. Aerospace Control And Application, 2011, 37(1): 50-54.

[4] 杜辉，张洪华.一类带液体晃动航天器的姿态控制[J]. 空间控制技术与应用, 2010, 36(2): 25-30.

DU H,ZHANG H H. Attitude control for a kind of spacecraft with fuel slosh[J]. Aerospace Control and Application, 2010, 36(2): 25-30.

[5] 胡锦昌，张洪华.月球着陆器最终下降段的制导与控制方法研究 [J]. 宇航学报, 2012, 33(11): 1577-1585.

HU J C,ZHANG H H. Guidance and control method for lunar lander’s final descent phase[J]. Journal of Astronautics, 2012, 33(11): 1577-1585.

[6] ASTOLFI A, KARAGIANNIS D, ORTEGA R. Nonlinear and Adaptive Control with Applications,Springer, London, 2008.

HoveringandAvoidanceMethodofLunarLandersBasedonAdaptiveControl

HU Jinchang1,2, ZHANG Honghua1,2, LI Maomao1,2

(1.BeijingInstituteofControlEngineering,Beijing100190，China;2.ScienceandTechnologyonSpaceIntelligentControlLaboratory,Beijing100190，China)

When mass and force uncertainties are taken into account, it will be difficult for lunar landers to hover on the designed height. To address this problem, we propose a new method for hovering and avoidance which is based on adaption.The core idea is to employ the position as the input of the observer for estimating and compensating the uncertainties. Compared with conventional PID methods, the proposed control strategy enjoys the properties of fast speed and small fluctuation, and it is able to realize high performance for hovering and avoidance. Numerical simulations demonstrate the effectiveness of the proposed approach.

lunar landing; hovering and avoidance; uncertainties of mass and thrust force; immersion and invariance.

*国家青年自然科学基金资助项目(61403031).

2017-05-08

V448.22

A

1674-1579(2017)06-0025-07

10.3969/j.issn.1674-1579.2017.06.005

胡锦昌(1984—)，男，高级工程师，研究方向为航天器姿态控制、非线性系统控制；张洪华(1963—)，男，研究员，研究方向为深空探测导航、制导与控制，非线性系统控制等；李毛毛(1990—)，男，博士研究生，研究方向为航天器导航、制导与控制.