正交试验法在空间自由漂浮机械臂控制参数寻优中的应用*

张瀚文

(北京控制工程研究所，北京 100190)

正交试验法在空间自由漂浮机械臂控制参数寻优中的应用*

张瀚文

(北京控制工程研究所，北京 100190)

针对空间自由漂浮机器人自适应控制参数的寻优问题，引入正交试验设计方法.综合考虑了各因素对试验结果的影响，通过较少的试验仿真次数即可快速获得较为理想的控制器参数，因此该方法对复杂系统控制器参数寻优具有较为实用的借鉴意义.实例证明，采用L81(340)正交表能较好地完成两自由度自由漂浮空间机械臂的14个控制参数寻优.

正交试验设计；空间自由漂浮机械臂；参数寻优

0 引 言

空间机器人控制系统的地面试验，如同人造卫星、导弹及反坦克导弹制导系统等的弹道试验一样，不宜多次实施实物试验或者不具备空间环境实物试验的条件，另外空间机器人控制系统进行大量的地面数学仿真耗费巨大的人力、物力，如何最快获取控制系统参数，同时保证较高的控制精度，就需要进行现代试验设计研究.正交试验设计方法就是一种广泛应用的，寻求最优水平组合，并且被证明是十分有效的不需要全面试验的高效率试验设计方法.正交试验设计是根据正交性从全面试验中挑选出部分有代表性的点进行试验，这些有代表性的点具备了“均匀分散，整齐可比”的特点，统计学家将正交设计通过一系列的表格来实现，这些表叫做正交表.

与现代试验设计相比，传统的仿真方法一次改变一个参数，计算量大，并且每个参数最优也不能保证所有因素组合起来是最优组合，更不能分析各因素对结果的影响程度.目前空间机器人的研究正在如火如荼的进行，对空间机器人控制系统进行现代试验设计，将最优化思想和要求贯穿于试验的全过程非常必要.本文要做的工作是通过合理高效的试验设计，减少试验次数，以较低的试验成本快速获得最优的自由漂浮空间机械臂控制系统模型控制器参数，缩短项目研制周期.

1 正交试验法

试验设计方法是一种用于安排试验和分析试验数据的数理统计方法.试验设计的目的就是通过一系列试验，使得能够观察和识别出引起输出响应变化的缘由.应用试验工具，可以对试验进行合理安排，对试验结果进行科学分析，以较小的试验规模(试验次数)，较短的试验周期和较低的试验成本，获得理想的试验结果和合理的结论.

对所有试验因素不同水平的自由组合都进行试验称为全局试验.从全部因素和水平的自由组合中选择部分组合进行试验称为部分试验.试验设计追求的目标之一就是要用尽量小的部分试验来实现全局试验所要达到的目的.

正交表A是n×k矩阵，它的第j列元素由数字1,2,3,…,mj所构成，矩阵A的任意两列都搭配均衡.在正交表Ln(m1×m2×…×mk)中，若m1=m2=…=mk=m,则为m水平正交表，或称为水平数相同的正交表，并简记为Ln(mk).下面以L9(34)正交表(表1)为例分析说明正交试验设计原理.

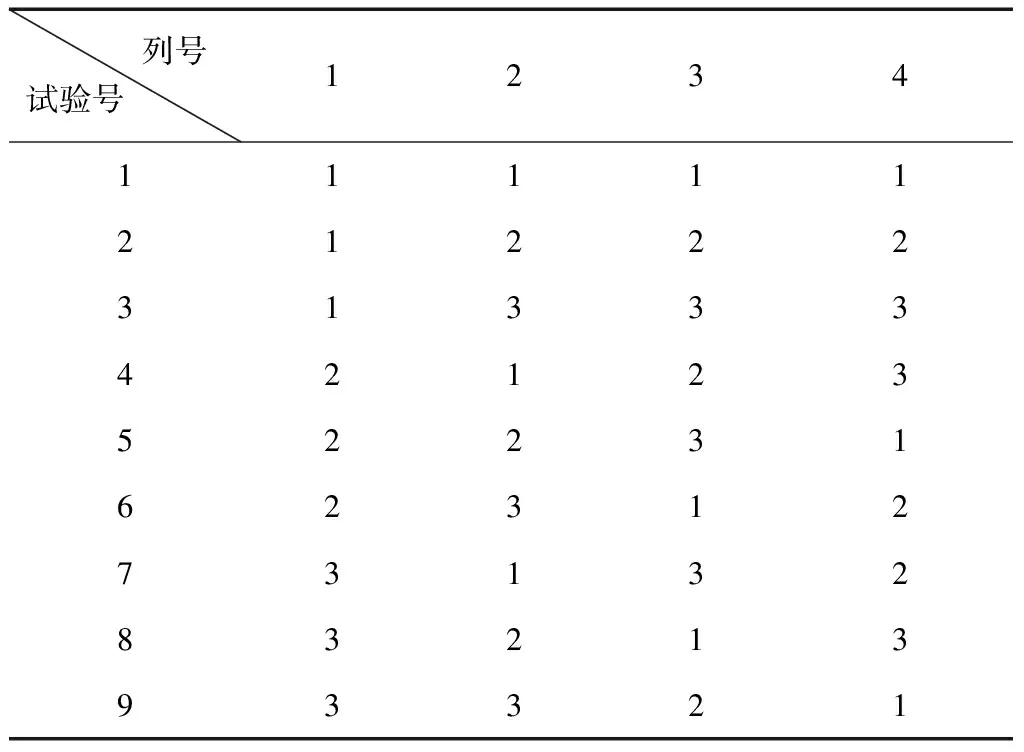
表1 正交表L9(34)Tab.1 Orthogonal array table L9(34)

如果做全面试验，需做L=33=27次，如图1所示的立方体包含了27个节点，可分别用来表示全面试验的这27种水平组合.若选用1、2、3列安排A、B、C3个因素，则总共只需安排9次试验，这9种水平组合即为从全面试验27种水平组合中挑选出来的.

比较图1和图2可以看出，图2中的圆点有3个特点：在立方体中的每一个面上，圆点数相同，都是3个；在立方体中的每一条线上，圆点数相同，都是1个；这两点能充分说明正交表所安排的试验方案，各因素水平的搭配是“均衡的”；通过正交表可以发现任意其他两个因素对第3个因素同一水平试验结果的影响大体相同，它们之间的差异是由于第3个因素取了不同水平所引起的，这使得第3个因素不同水平间有了可比性，它是选取各因素优秀水平的依据，这叫做“综合可比性”.因为正交表安排试验具有“均衡搭配性”和“综合可比性”这两大特点，因此才能取得减少试验次数的良好效果[1].

由此可见，正交试验设计主要优点表现在如下几个方面：

1)能在所有试验方案中均匀地挑选出代表性强的少数试验方案.

2)通过对这些少数试验方案的试验结果进行统计分析，可以推出较优的方案，而且所得到的较优方案往往不包含在这些少数试验方案中.

3)对试验结果作进一步的分析，可以得到试验结果之外的更多信息，如各试验因素对试验结果影响的重要程度、各因素对试验结果的影响趋势等.

对给定的因素和水平数，要得到相应的正交表(如果存在)是不容易的.目前流行的各种正交表是许多数学家长期努力的结果.构造正交设计的方法主要有：Hadamard矩阵构造，正交拉丁方构造，有限域构造、MI构造、编码构造、有限几何构造法[2-4]等，这里不做详细分析，只列出目前数学家们已经给出的很多常用的正交表[5]，如表2所示.

表2 目前常用的正交表Tab.2 Current orthogonal array table

2 空间自由漂浮机械臂控制参数寻优

2.1 空间机械臂动力学模型

用向量q描述自由飞行空间机械臂的位置，用力矩向量τ表示执行器输入，其动力学方程可以写成如下形式[6-7]：

(1)

当航天器处于自由漂浮状态时，式(1)可写成如下形式：

(2)

(3)

式中：M(q)为惯量矩阵，

Mbb为航天器惯量矩阵，Mbb∈R3×3；

Mbm为航天器和机械臂的耦合惯量矩阵,Mbm∈R3×n；

Mmm为机械臂的惯量矩阵，Μmm∈Rn×n；

Cbb为航天器的离心力和科氏力矩阵，Cbb∈R3×3；

Cbm为航天器和机械臂的耦合离心力、科氏力矩阵，Cbm∈R3×n；

Cmb为机械臂和航天器的耦合离心力、科氏力矩阵，Cmb∈Rn×3；

Cmm为机械臂的离心力和科氏力矩阵，Cmm∈Rn×3；

τm为机械臂的关节驱动力矩，τm∈Rn.

2.2 空间自由漂浮机械臂自适应控制

自由漂浮控制模式下，姿态轨道控制系统处于关闭状态，能节省不可再生燃料的消耗，延长系统的使用寿命.本文采用的自适应控制方法依据参考文献[7].

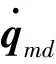
(4)

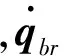
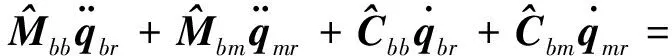
(5)

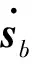
(6)

(7)

(8)

(9)

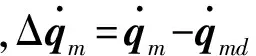
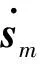
(10)

(11)

设关节空间自适应控制律为

(12)

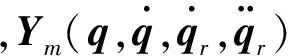
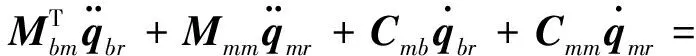
(13)

其中，ad为自由漂浮机械臂的未知动力学参数矢量.

动力学参数自适应律选择为

(14)

其中，

2.3 空间自由漂浮机械臂自适应控制参数寻优

(1)两自由度自由漂浮空间机械臂的动力学模型

为便于Matlab编程仿真，将两自由度空间机械臂的动力学方程写成如下形式：

(15)

其中，空间机械臂的动力学参数ad=[a1a2a3a4a5a6a7a8]T.其中，qb=q0为航天器姿态角，qm=[q1q2]为机械臂的关节角矢量.

空间两自由度自由漂浮机械臂物理参数如表3所示.

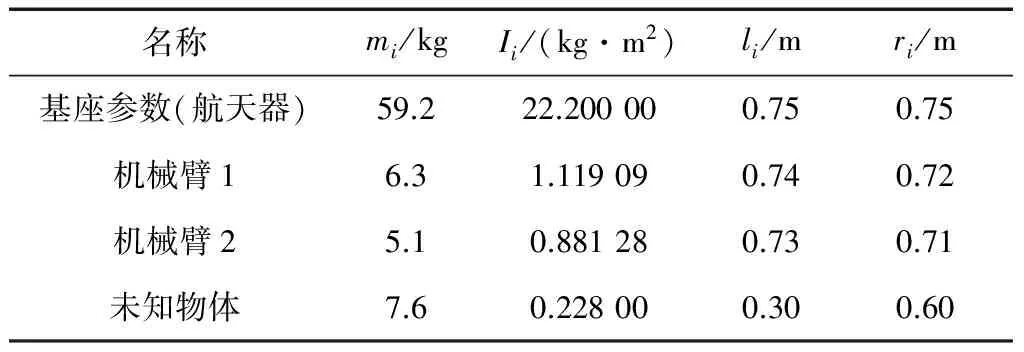
表3 两自由度自由漂浮机械臂的物理参数Tab.3 Physical parameters of two-DOF free-floating space manipulator

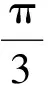
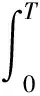
取控制器参数β0=10I，Km=20I，Kb=20I，Γd=25I，计算指标IITAE=[1.934 1 1.689 9]T，仿真结果如图4～6所示.

(2)两自由度自由漂浮空间机械臂控制参数寻优

选用正交试验设计的方法优化自由漂浮机械臂空间自适应控制参数.其中，共计14个控制参数，给定这些参数初始的范围如表4～6.

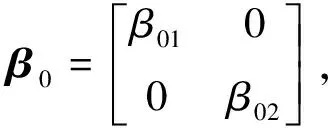
表4 两自由度自由漂浮机械臂控制器参数初始值Tab.4 Initial values of β01…Kb2

表5 两自由度自由漂浮机械臂控制器参数初始值Tab.5 Initial values of Γd1…Γd6

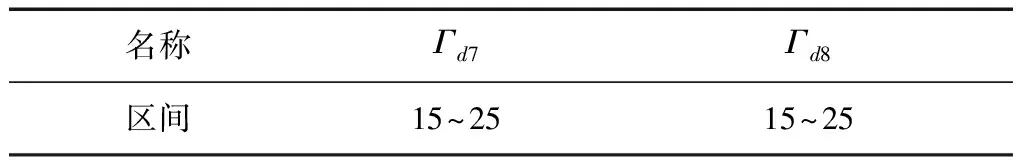
表6 两自由度自由漂浮机械臂控制器参数初始值Tab.6 Initial values of Γd7and Γd8

为确保试验精度，每个参数在正交试验设计时选取3个水平，即参数范围两端点和中间点.每次寻优后各参数优化后区间是原区间的一半，如区间是(5～15)的范围时，3个水平点分别是5、10和15，单次优化后参数区间会缩小为(5～10)或者(10～15)，如此循环.

下面给出正交设计优化空间机械臂控制算法参数的流程框图如图7所示.

为保证试验设计优化精度，这里选择L81(340)正交表，下面利用机械臂实际行走路径和目标路径间的累计误差IITAE值最小为目标开展优化，经过Matlab编程仿真，参数优化结果如表7所示.

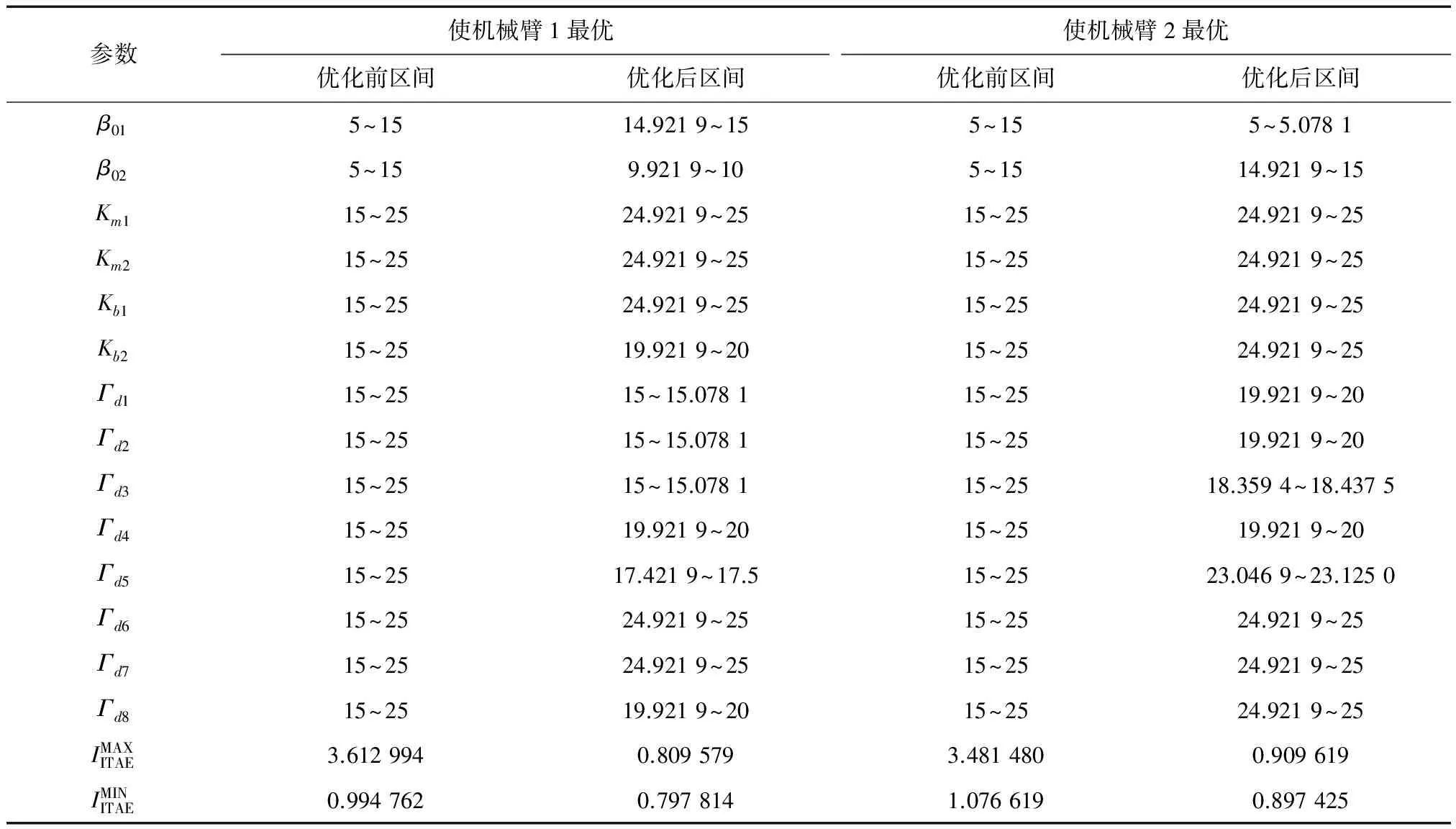
表7 正交设计优化结果Tab.7 Optimized results with orthogonal array design

与全局优化相比，正交试验设计优化结果不如全面试验设计优化结果最佳，但是以调用IITAE函数为例，正交试验设计优化法仿真调用IITAE函数的次数比传统的全局优化法大大减少.从表8可以看出，将控制器参数区间范围优化到0.1以内，需要做7次循环，正交试验设计优化方法调用IITAE函数567次，而全局优化需要33 480 783次，如表8所示.

表8 正交试验设计优化和全局优化比较Tab.8 A comparison between optimized results with orthogonal array experimental design and optimized results on the full scale 次

以上说明，经过正交试验设计优化后，参数区间范围都缩小至0.1以内，IITAE目标值显著缩小并且稳定性提高，试验仿真次数大幅下降，达到优化目的.

与传统的控制参数寻优相比正交设计法有以下优点：

1)正交试验设计可以同时考虑多个参数变化的均匀组合，传统的仿真计算只能一次考察一个参数对系统指标的影响；

2)通过正交试验设计可以大大减小试验次数.

3)对于空间机器人控制这种复杂的控制系统，其参数之间不可避免地存在耦合，利用正交实验设计方法进行参数寻优时，可以同时考虑耦合因素对系统的影响，避免了系统解耦；

4)正交试验设计可以实现多指标参数寻优，采用综合平衡法、综合评分法等找出使每个指标都尽可能好的试验方案.

当然，正交试验设计方法在提高参数寻优速度的过程中，因为没有进行完全的试验仿真，寻优结果精度不如全局试验.虽然没有传统的全局仿真试验精度高，但是在参数寻优精度满足要求而速度要求很快的情况下更能体现其优越性，实用性更高.

3 结 论

将正交试验设计和计算机仿真相结合，提出了一种新的空间机器人控制参数寻优方法.利用正交试验设计，以较少的试验次数成功将两自由度自由漂浮空间机械臂自适应控制参数区间优化至给定范围，以较低的试验成本快速获得较为理想的控制参数，证明了利用正交试验设计方法进行复杂系统参数寻优的可行性.本文也为其他系统参数寻优提供了一种新思路.

目前空间机械臂大多都具有6个甚至6个以上的自由度，其控制模型更复杂，参数寻优更困难.未来可以通过设计更多因素更多水平的正交表，将正交试验设计法应用在6自由度以上机械臂控制参数寻优，实现参数的快速优化.这种复杂的多因素试验，常常会遇到各因素间交互作用的问题，各试验因素水平数不等的情况，以及多指标试验设计的情况等，需要按照实际需求设计合理合用的正交表，或对选取的正交表进行适当改造.如何获取试验效果最佳的正交表将是今后研究工作的难点.

[1] 邱轶兵．试验设计与数据处理[M]．合肥：中国科学技术大学出版社，2008：77-80.

[2] 任露泉．试验设计及其优化[M]．北京：科学出版社，2009：7-51.

[3] 马成良 张海军 李素平．现代试验设计优化方法及应用[M]．合肥：郑州大学出版社，2007.

[4] 方开泰，马长兴．均匀设计和正交设计的关联和比较[C]//中国数学会均匀设计理论及其应用研讨会．香港：中国数学会，1999.

[5] WARREN F K, CHUNG Y S. Some new orthogonal arrays [J].Statistics & Probability Letters，2005，75(3):169-178.

[6] JEAN-JACQUES E.SLOTINE W L.应用非线性控制[M]．程代展译．北京：机械工业出版社，2009:266-284.

[7] 王汉磊．机器人自适应雅克比控制[D]．北京：北京控制工程研究所,2009.

[8] DORF R C, BISHOP R H.现代控制系统[M]．赵千川，冯梅译．北京：清华大学出版社，2008:243-244.

TheOrthogonalArrayExperimentalDesignMethodforOptimizingControlParametersofFree-FloatingSpaceRobotManipulator

ZHANG Hanwen

(BeijingInstituteofControlEngineering，Beijing100190,China)

An orthogonal array experimental design method is developed to optimize the control system parameters of a free-floating space robot manipulator. The experiment results show that it is very quick and precise in approaching the appropriate value of every control parameter with the orthogonal array experimental design method. The method is very useful for optimizing control parameters of complex systems. For example, L81(340) orthogonal array can realize the optimization of fourteen adaptive control parameters which are selected randomly.

orthogonal array experimental design method； free-floating space robot manipulator； parameters optimizing

*国家重点基础研究发展计划(973)资助项目(2013CB733100).

2016-09-17

V44

A

1674-1579(2017)06-0047-07

10.3969/j.issn.1674-1579.2017.06.008

张瀚文(1984—)，女，工程师，研究方向为机器人自适应控制.