星敏感器姿态测量相对基准偏差在轨标校方法研究*

雷拥军

(1.北京控制工程研究所，北京 100094；2.空间智能控制技术重点实验室，北京 100094)

星敏感器姿态测量相对基准偏差在轨标校方法研究*

雷拥军1,2

(1.北京控制工程研究所，北京 100094；2.空间智能控制技术重点实验室，北京 100094)

对航天器星敏感间姿态测量基准偏差在轨标校及性能评估问题进行研究.建立包含敏感器安装误差与测量误差的星敏感器模型，针对两种不同形式的安装误差模型，推导出相应的观测方程，基于卡尔曼滤波方法设计相对基准偏差估计器，并比较分析两种估计器实际应用特点.然后针对在轨实际应用，给出一种基于敏感器光轴夹角的标校性能评估方法，通过数学仿真验证星敏感器相对基准偏差的标校的有效性，并基于在轨数据的标校应用获取相对基准偏差在轨特性.

航天器；姿态测量；安装误差标校；卡尔曼滤波；星敏感器

0 引 言

由于受地面的精测条件和精测精度限制，以及发射振动、结构在轨应力释放和空间环境影响等，姿态敏感器难免存在安装测量误差和结构形变导致的误差，即使同一航天器上不同星敏感器的误差也往往不一样，从而使得星敏感器之间的测量基准不一致.测量基准的不一致，除了直接影响星敏感器组合对星体姿态确定精度外，定姿星敏感器组合变化导致的姿态基准切换往往对星体估计姿态、星体指向及星体稳定度均产生一定程度的波动，严重情况下甚至影响高分辨观测卫星的载荷工作.在高精度对地遥感及天文观测中，为克服敏感器相对基准变化对姿态测量的影响，国内外航天器普遍采用的措施是将敏感器与载荷基于一体化稳定结构同基准安装并辅以高精度温控[1-2]，以期实现姿态测量与载荷指向基准统一.

航天器在轨运行时所处空间环境发生变化，敏感器相对基准也会受到不同程度的影响.对星敏感器在内的姿态敏感器进行在轨相对基准标校是消除在轨相对基准偏差的有效手段[3-8].自早期OAO-A2航天器建立星跟踪器安装误差模型并在轨对其标校[6]以来，基于矢量测量的姿态敏感器相对基准标校主要发展为批处理最小二乘标校方法[7-8]、扩展QUEST标校方法[9]和基于滤波的标校方法[6,10-11]等几类.前两种标校方法仅能在地面进行事后处理，无法适应敏感器相对基准偏差在轨发生变化而需实时标校的应用需求；目前大部分基于滤波标校方法一般将敏感器相对基准偏差参数扩维为状态与星体姿态一同估计，并广泛应用于实际地面事后处理，但直接应用于在轨实时标校则显得计算量过大.文献[6]分别对星敏感器相对基准偏差标校与姿态估计分开设计独立的滤波器，极大地简化在轨应用复杂程度，但对基准偏差标校的滤波器参数如何设计并未给出相应理论依据.

针对星敏感器相对基准偏差在轨实时标校问题，本文在星敏感器测量模型建立中考虑了两种安装误差参数描述方式，并根据相应观测方程基于卡尔曼滤波方法设计相对基准偏差参数估计器.此外，针对在轨实际应用评估需要，对在轨标校性能评估手段进行探讨性研究.

1 星敏感器安装及测量误差描述

星敏感器测量轴在敏感器测量坐标系分别为

其在星体坐标系下标称安装方向分别为Bx0、By0与Bz0，则星敏感器在星体坐标系下标称安装矩阵M0为

(1)

标称安装阵M0可由地面精测数据得到.在轨结构形变后，星敏感器实际安装矩阵M在星体坐标系下将与标称安装M0存在偏差.假设星体坐标系相对惯性坐标系的真实姿态为方向余弦阵CBI，则星敏感器测量坐标系相对惯性坐标系的方向余弦阵为

CSI=MCBI

(2)

星敏感器测量轴在惯性空间的真实指向为Ix、Iy和Iz，则有

(3)

偏差矩阵ΔM可由绕标称安装坐标系旋转的3个角度得到，记绕三轴矢量旋转角度依次为θ1、θ2和θ3，且均为小量，则偏差阵ΔM可表示为

(4)

根据偏差矩阵ΔM，星敏感器实际安装矩阵可表示为如下两种不同形式：

M=MoΔM

(5a)

与

M=ΔMMo

(5b)

其中式(5a)安装误差描述为目前标校系统所采用方式[6]，式(5b)为本文给出的另外一种描述形式.为加以区分，根据其结构不同分别称之为右乘偏差形式和左乘偏差形式.矩阵ΔM在两种描述中的物理含义有所不同，其中在式(5a)描述中可等效为星体坐标系相对初始的变化，而在式(5b)中可看作星敏感器测量坐标系相对星体坐标系发生形变.

考虑星敏感器测量误差

(6)

其中随机变量Δφ、Δθ与Δψ为三轴测量噪声等效角，即等效为沿真实测量轴各旋转的小角度值，且为互不相关的零均值白噪声，其方差为

其中σxy、σz为大于零的常数，有时也分别称之为光轴指向精度与横轴指向精度.由于星敏感器小视场光学成像的姿态测量特点，一般为σz>σxy.

考虑航天器在轨结构形变及测量误差，星敏感器测量输出为

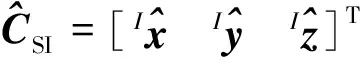
(7)

2 星敏感器测量基准间标校方法

为了描述的简洁性，对于任何两星敏感器组合(两敏感器以i=1,2进行区分)，不失一般性在本文中均假定其测量性能一致(当性能不一致时直接沿本文过程可得到相似结论)，即测量噪声等效角Δφi、Δθi与Δψi为互不相关的零均值白噪声且其方差为

以下假定以星敏感器1的测量作为姿态基准，分别对式(5)所示两种形式安装误差模型进行基准偏差估计的滤波器设计，以对星敏感器2基准偏差进行标校，并比较两种滤波器形式的差异.

2.1 基于右乘偏差形式的测量方程

由式(7)及星敏感器实际安装矩阵式(5a)，有如下关系式：

(8)

假设安装偏差角均为小量，则有

(9)

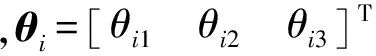
利用式(9)，(8)可表示为

(10)

即有

(11)

忽略二阶小量时，式(11)右端第二项展开后的表达式如下：

(12)

由式(11)、(12)可得两星敏感器基准偏差为

(13)

其中，S0(·)与SΔ(·)分别为矩阵S0与SΔ对应元素.

由式(13)可建立星敏感器间姿态基准标校系统的观测方程为

(14)

2.2 基于左乘偏差形式的测量方程

(15)

记

则有

由式(7)及星敏感器实际安装矩阵式(5b)，有如下关系式：

(16)

对于式(15)给出的观测量，在忽略二阶小量时可由式(16)得到如下关系式：

Z=HΔθ21+ΔZ

(17)

其中

且ΔZ的均值及方差阵为

E(ΔZ)=0，R=E(ΔZΔZT)

由ΔZ表达式及给出的星敏感器测量模型可知，其均值为零且方差阵R=E(ΔZΔZT)为与星敏感器标称安装及测量精度相关的常系数矩阵，且方差阵可直接由其误差表达式经过简单运算得到.

2.3 基于卡尔曼滤波方法的基准偏差标校

假设星敏感器在轨形变误差维持不变或随时间缓慢变化，则状态方程可近似表示为

Δθ21(k+1)=Δθ21(k)+nθ(k)

(18)

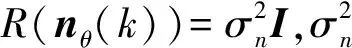
对于由状态方程式(18)与观测方程式(14)或与式(17)组成的随机系统，采用卡尔曼滤波方法设计滤波器对相对基准偏差进行估计.对于不同观测方程所对应的两系统的滤波器均可写为如下形式：

滤波方程：

增益阵：

K(k)=P(k)HTR-1(k)

预测误差方差阵：

滤波误差方差阵：

P(k)=(I-K(k)H)P(k/k-1)

初值可选为

其中，k为滤波周期数，Z(k)、H及R(k)分别对应于式(14)或式(17)的测量方程的观测向量、系数矩阵与噪声ΔZ的方差阵.

上述两滤波标校系统除了各参量具体表达式不一样外，其他区别还在于：

1)基于左乘安装偏差描述形式的观测方程中的测量噪声方差阵为仅与标称安装相关的常系数阵.对于完全能控与完全能观线性定常随机系统，当滤波时间充分长时滤波误差方差阵趋于某一正定常数阵且增益阵趋于某一常系数阵[12]，因此对由式(17)～(18)组成的随机系统可设计出稳态卡尔曼滤波器以简化在轨计算，对应稳态增益阵K可通过求解相关代数Riccati方程而得到.

2)对于基于右乘安装偏差描述形式，由式(13)可知，将以星敏感器1为基准更换为以星敏感器2为基准时，对应的相对基准偏差Δθ12满足关系：

Δθ12=θ1-θ2=-Δθ21

这直观的特性对于左乘安装偏差描述是不具有的.

由式(17)给出的观测方程系数矩阵，并结合状态方程式(18)所给出为单位矩阵的状态矩阵，很显然易知在某些特定敏感器相对安装下使得矩阵H的行列式|H|为零时会出现标校系统不是完全随机可观测的.为避免该情况发生，可重新选取观测度比较好的其它测量轴间组合，或在式(15)观测向量上适当增加两星敏感器其它轴间组合的信息，对应的观测方程表达式可直接由式(16)导出.实际工程中星敏感器的光轴指向一般不平行安装，通过沿光轴旋转来调整横轴指向也可加以避免.不失一般性，本文均假定所选观测量均可使标校系统满足可观测条件.

3 相对基准标校性能评估方法

由于在轨星敏感器的实际安装形变是不确知的，地面需结合基准标校结果及测量对标校精度进行评估，一般可利用由两星敏感器测量输出计算的两测量轴夹角与由标校安装计算的对应夹角的两者偏差(称之为夹角残差)作为评估依据.由于星敏感器输出光轴指向精度要远远高于横轴，即σz>σxy>0，因而首选光轴夹角残差作为评估依据.

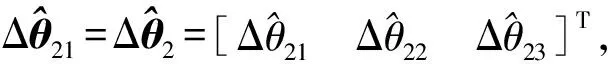
(19)

(20)

其中nIz为随机项.

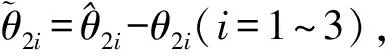
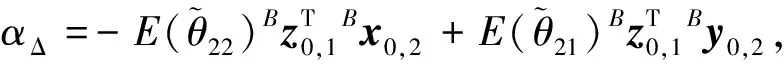
(21)

由式(19)与(20)可得两光轴夹角偏差为

(22)

将偏差ΔαZ12简称为标校安装与测量的光轴夹角偏差，其期望值为

考虑星敏感器测量误差为小量，由式(20)有

≈cos(αZ12)-nIzsin(αZ12)

(23)

在忽略敏感器测量误差二阶小量时，由式(7)及测量噪声特性可求得

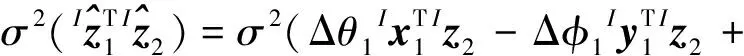
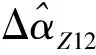
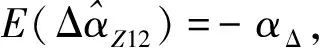
(24)

4 仿真分析及应用

4.1 数学仿真分析

两星敏感器在星体下的标称安装为

其光轴指向精度3σxy为1″(3σ)和横轴指向精度3σz为20″(3σ).以星敏感器1为基准，按安装偏差模型式(5b)形式对星敏感器2测量轴不同形式的基准偏差进行标校仿真验证.

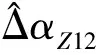
(1)基准偏差为常值时的标校

以星敏感器1为基准，按安装偏差描述式(5b)设定星敏感器2测量轴常值基准偏差分别为-30″、30″与0″.由测量模型式(7)获取星敏感器输出数据进行标校，结果如图1所示，当滤波稳定后三轴相对基准偏差参数估计值均小于0.1″(3σ).

采用估计值对星敏感器2安装进行修正，由测量数据计算得到的光轴夹角残差数据如图2所示.对标校后残差数据统计得其均值-0.01″和3倍均方差1.424″，与极限精度1.414″(3σ)非常接近，从而表明了基准偏差标校的有效的.

(2)基准偏差包含周期项时的标校

除了上述常值安装偏差外，在星敏感器2测量轴的X轴与Z轴上还分别引入幅值1.0″和2″的轨道周期频率变化误差，以及Z轴上幅值为0.5″的2倍轨道周期频率误差.计算得到的基准偏差和滤波得到的三轴基准偏差参数分别如图3所示，由仿真结果可知，所采用标校算法对变化的基准偏差估计具有较好的动态性能.

采用估计值对星敏感器2安装进行修正，标校前、后光轴夹角残差数据如图4所示.对标校后数据进行统计得其均值-0.1488″和3倍均方差1.4589″(3σ).上述统计结果可知无论是对于均值还是方差，与基准偏差仅为常值情况均略有所增大.

4.2 基于在轨数据的标校应用及分析

针对某在轨卫星长达7个轨道周期(一个轨道周期约5 960 s)的两星敏感器输出遥测数据，以其中之一作为测量基准，在地面采用式(5b)安装偏差模型的滤波标校方法对另一星敏感器相对基准偏差进行标校，得到星敏感器2的三轴相对基准偏差参数估计如图5所示.从结果中可以看出，与星敏感器标称安装相比，在轨星敏感器间基准形变最大接近100″，且包含有幅值约为16″的周期波动.

对其中X轴姿态相对基准偏差估计数据进行频谱分析，结果如图6所示，可以看出除了常值项外，估计中还明显含有类轨道周期误差，其中星敏感器相对基准变化周期主要为幅值约12"的1倍轨道周期成份.此外，还存在1/2～1/15的不同轨道周期成份，但其相应幅值相比1倍轨道周期幅值明显要小，其中1/2轨道周期幅值约为1倍轨道周期幅值的1/4.由此可见，空间热环境对敏感器相对基准偏差影响呈现复杂特性.

5 结 论

本文针对星敏感器基于安装偏差矩阵右乘和左乘两种不同形式的安装偏差描述，分别给出了相应的相对基准标校算法.针对实际在轨应用性能评估需求，给出了基于敏感器光轴夹角的性能评估方法.由两者相对基准标校滤波标校方法比较可知，除了观测方程系数阵外，后者相比前者还具有测量误差方差阵具有与标称安装相关的常系数特点，从而使其在滤波器设计及性能优化方面具有一定优势，结合数学仿真对其有效性进行了验证，并进一步基于在轨遥测数据标校应用及分析，获取了相对基准偏差在轨的一些特性.

[1] 徐庆鹤, 范立佳, 高洪涛, 等. 遥感卫星平台与载荷一体化构型[J]. 航天返回与遥感, 2015, 35(4): 9-16.

XU Q H, FAN L J, GAO H T, et al. Intergrated configuration design of platform and payload for remote sensing satellite[J]. Spacecraft Recovery & Remote Sensing, 2015, 35(4): 9-16.

[2] 李果, 孔祥皓, 刘凤晶, 等. “高分四号”卫星遥感技术创新[J]. 航天返回与遥感, 2016, 37(4): 7-15.

LI G, KONG X H, LIU F J, et al. GF-4 satellite remote sensing technology innovation[J]. Spacecraft Recovery & Remote Sensing, 2015, 37(4): 7-15.

[3] PITTELKAU M E. Survey of calibration algorithms for spacecraft attitude sensor and gyros[J]. Advances in the Astronautical Sciences, 2008, 129(1): 651-706.

[4] RAO J S, PULLAIAH D, PADMASREE S, et al. Star tracker alignment determination for resourcesat-I[C]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Washington D.C： AIAA, 2004.

[5] 黎康, 乔国栋, 刘新彦. 高分四号卫星控制方案设计特点及在轨实现[J]. 空间控制技术与应用, 2016, 42(6): 1-8.

LI K, QIAO G D, LIU X Y. Highlights of attitude and orbit control system (AOCS) for GaoFen-4 satellite with on-orbit verification[J]. Aerospace Control and Application, 2016, 42(6): 1-8.

[6] 王淑一, 刘祥, 陈超. 资源三号卫星控制系统概述及在轨验证[J]. 空间控制技术与应用, 2015, 41(2): 1-5.

WANG S Y, LIU X, CHEN C. Overview of control system and on-orbit test for ZY-3 satellite[J]. Aerospace Control and Application, 2015, 41(2): 1-5.

[7] DEDJARDIN R. In-orbit star-tracker misalignment estimation on the OAO[C]//Proceedings of the Symposium on Spacecraft Attitude Determination. EI Segundo: CA, 1969.

[8] HASHMALL J A, AATANSON G, GLICKMAN J, et al. Compensation for time-dependent star tracker thermal deformation on the Aqua spacecraft[C]//The 18thInternational Symposium on Space Flight Dynamics. Munich: Germany, 2004.

[9] SHUSTER M D, PITONE D S. Batch estimation of spacecraft sensor misalignments, I. Relative alignment estimation[J]. Journal of the Astronautical Sciences, 1991, 39(4): 519-546.

[10] LAI K L, CRASSIDIS J L, HARMAN R R. In-space spacecraft alignment calibration using the unscented filter[C]//Proceedings of AIAA Guidance, Navigation, and Control Conference and Exhibit. Washington D.C.: AIAA, AIAA 2003-5563.

[11] LAI P C, PARK S K, TUNG F C. Kalman filter design for jwst spacecraft attitude determination system[J]. Advances in the Astronautical Sciences, Spaceflight Mechanics, 2006, 124(1): 125-143.

[12] 王志贤. 最优状态估计与系统辨识[M]. 西北工业大学出版社，西安, 2004.

RelativeAlignmentErrorCalibrationMethodforStarSensorsofSpacecraftinOrbit

LEI Yongjun1,2

(1.BeijingInstituteofControlEngineering,Beijing100190,China；2.ScienceandTechnologyonSpaceIntelligentControlLaboratory,Beijing100190,China)

The problems of star sensors relative misalignment calibration and its performance evaluation are investigated. First, an integrated star sensor model including misalignment and measurement error is established. Then, measurement equations for alignment calibration are deduced individually for two different misalignment descriptions, and corresponding estimators are also designed based on Kalman filtering method. Meanwhile, the comparison is present between these estimators when applied to in-flight spacecraft calibration. Furthermore, an evaluation method is developed by angle between optical axes of dual star sensors. Finally, the effectiveness of the proposed calibration method is demonstrated by numerical simulations, and the characteristic of in-orbit star sensors misalignment relative to each other are also obtained by applying the proposed method with telemetry data．

spacecraft； attitude measurement； alignment error calibration； Kalman filtering； star sensor

*北京市自然科学基金资助项目(4162070).

2017-08-01

V448.2

A

1674-1579(2017)06-0001-07

10.3969/j.issn.1674-1579.2017.06.001

雷拥军(1971—)，男，研究员，研究方向为航天器姿态控制.