共线三星库仑编队动力学与自适应控制研究*

施 强，袁长清，孙云龙，于海莉

(空军航空大学飞行器与动力系，吉林 130022)

共线三星库仑编队动力学与自适应控制研究*

施 强，袁长清，孙云龙，于海莉

(空军航空大学飞行器与动力系，吉林 130022)

针对地球同步轨道处共线三星库仑编队队形保持的自适应控制问题进行研究,建立共线三星库仑编队在地球同步轨道的非线性相对运动动力学模型，研究仅使用库仑力作为控制力，实现共线三星库仑编队径向静态稳定的控制方案，并在库仑力建模中考虑德拜效应的影响.基于建立的非线性化动力学模型，同时考虑到外部扰动力的影响，设计三星共线库仑编队在地球同步轨道的构型保持自适应控制律，并利用Lyapnuov稳定性理论证明系统的闭环稳定性，进行数值仿真.

库仑编队；地球同步轨道；构型保持；自适应控制

0 引 言

近年来，库仑力卫星编队作为一种新兴的近距离编队技术受到越来越多的关注[1-2].库仑力编队利用卫星间的静电引力或斥力作为控制力，通过设计适当的控制律来控制编队的构型、姿态以及编队中卫星间的距离[3].库仑力作为一种非接触作用力，它源于带电卫星间静电力的相互作用，其比冲高达1013s[4]，因此它是一种十分高效的控制力.在给卫星充电时只需消耗几瓦特的功率，且它可以利用太阳帆板提供的电能不需要消耗燃料，不会对邻近卫星产生羽化污染，因此库仑力编队技术能够被用于执行高轨道或深空长任务周期的近距离或极近距离卫星编队任务.

三星及多星库仑力编队动力学模型的强耦合性和非线性特点，给其稳定性分析及控制律的设计带来了诸多难题.国内外学者多对二星库仑力编队进行研究，Inampudi等[5-6]人运用拉格朗日函数建立两星库仑编队在地-月平动点处的动力学模型，并分别讨论在地-月系平动点处两星库仑编队在径向方向、轨道切线方向和轨道面法线方向的稳定性问题.Wang等[7]研究了地球同步轨道两卫星自旋库仑虚拟结构控制问题，设计全状态反馈电荷控制器，并应用Lyapunov稳定性理论，证明闭环系统是渐近稳定的.黄静[8]针对于平动点附近处二星虚拟绳系库仑力系统姿轨耦合控制问题，首先采用欧拉-拉格朗日方程对二体卫星建模，设计了非线性二次型最优控制器实现了对二体绳系系统的长周期稳定控制.张皓等[9]提出了一种使用航天器间库仑力实现悬停轨道的方法，并通过对开环控制和闭环控制的分析，给出了利用库仑力技术实现悬停轨道的实施方案.

在三星库仑编队方面，Schaub等[10-11]针对3个航天器对称编队构形，应用线性控制理论，设计反馈控制律，并讨论闭环系统稳定性.Hussein等[12]于2007年首次研究库仑虚拟结构的反馈控制问题，考虑三结点共线虚拟结构，应用线性化相对动力学方程设计了电荷反馈控制律.Hogan等[13]研究了在深空环境下的旋转三星库仑编队在二维平面内的相对运动模型，并以等质量共线三星编队为例进行分析.Jones[14]在文献[13]的基础上，基于非线性平面外解耦模型对深空环境下共线三星库仑编队的面外运动稳定性进行了分析，并设计了非线性控制律.文献[15]对六星库仑-绳系编队的双四面体对顶双锥型结构进行了研究，运用拉格朗日方程建立了其相对动力学方程，并对其开环控制进行分析.王婷等[16]研究了等质量五星库仑编队的静态构型问题.

上述研究在建立库仑力三星相对动力学模型时，既没有考虑地球等天体间引力对三星编队的影响，也没有考虑外界环境对于编队的干扰影响.本文选取地球同步轨道环境为研究背景.考虑地球引力、外界干扰、以及德拜效应的影响，以库仑卫星编队系统为研究对象，运用拉格朗日方程，建立了共线三星库仑力编队的非线性相对运动动力学模型.本文利用库仑力作为控制力，设计了共线三星库仑编队自适应控制律，同时考虑到未建模的扰动力的影响，并进行数值仿真验证.

1 动力学模型的建立

假设地球的质量为M，为了描述卫星之间的相对运动，建立Hill轨道坐标系H：{Or,Oθ,Oh}，Or沿地球半径指向背离地心方向，Oθ指向卫星编队质心的速度方向，Oh指向卫星轨道角速度方向，Oh与Or,Oθ构成右手系(如图1所示).用ri表示库仑力编队中第i颗卫星在地心惯性坐标系中的位置，rc为编队质心在惯性坐标中的位置矢量，第i颗卫星相对编队质心的位置矢量ρi=ri-rc，则第i颗卫星在Hill坐标系中的位置矢量为：

(1)

这里左上角标“H”表示矢量在Hill坐标系中的投影.

下面以整个库仑卫星编队系统为研究对象，建立多颗库仑力卫星编队飞行的非线性相对运动动力学模型.该模型也可以用来描述其他类型的非接触力卫星编队的相对运动.

1.1 系统动能

设第i颗卫星的质量为mi，第i颗卫星在惯性坐标系下的位置矢量可以表示为

(2)

式中，rc为库仑力卫星编队质心在惯性坐标中的位置矢量.

第i颗卫星的绝对速度可表示为

vi=vρ+vo

(3)

(4)

则第i颗卫星的动能为

(5)

从而我们可以得到由N颗卫星组成的库仑力卫星编队的系统动能为

(6)

1.2 系统势能

对于地球同步轨道处的多星库仑力卫星编队系统，其系统势能包括由地球引力产生的重力势能和卫星间的库仑力势能.

对于N星库仑力编队系统，其重力势能可以表示为

(7)

(8)

式中，ti为ρi的单位向量，u是rc的单位向量.

对于N星库仑力编队系统，其库仑力势能为

(9)

1.3 共线三星库仑编队相对运动动力学方程

对径向共线三星库仑编队进行分析，假设该三星库仑编队为径向方向相连的刚体结构，建立坐标系B:{b1,b2,b3}如图2所示，其中b1始终沿ρ13方向，若卫星编队无位置和速度偏差，b2沿轨道切线方向，b3与b2、b1构成右手系，则坐标系B与Hill轨道坐标系H完全重合.将绕b1轴的转角定义为偏航角φ，假定零姿态角情形b2标称方位指向飞行方向，则绕该轴的转角定义为滚转角θ，绕b3轴的转角定义为俯仰角ψ.

设3颗卫星的质量分别为m1、m2、m3，根据质心条件可以得到

m1ρ1+m2ρ2+m3ρ3=0

(10)

由图3知

(11)

式中：ρ1b1、ρ2b1、ρ3b1分别为星1、星2、星3在B坐标系下b1轴上的坐标；l1为卫星1与卫星2之间的距离，l2为卫星2与卫星3之间的距离.

联立式(10)～(11)可求得，在图2构型中，在坐标系B下，ρ1、ρ2、ρ3为

(12)

本文采用3-2-1(ψ-θ-φ)的欧拉角旋转，由于假设卫星视为质点，该共线三星编队为刚体结构.因此，绕b1方向转动的偏航角φ可以忽略，即φ=0，则坐标系B与希尔坐标系H之间的坐标转换矩阵为

(13)

在希尔坐标系H中，卫星i的位置向量为

(14)

将式(12)～(13)代入式(14)我们可知在希尔坐标系H中3颗卫星的位置矢量为

(15)

求导得速度矢量分别为

(16)

式中：

将式(4)、(15)、(16)分别代入式(6)、(8)、(9)可以得到径向共线三星库仑编队的系统动能T为

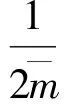
(17)

重力势能为

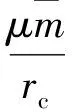
(18)

库仑力势能Ve为

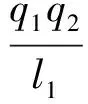
(19)

共线三星库仑力编队的系统拉格朗日函数为[5]:

L=T-(Vg+Ve)

(20)

拉格朗日方程为：

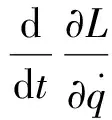
(21)

其中Qi为第i颗星所受到的广义力(不包括地球重力项和库仑力项).

将式(17)～(19)代入式(21)得共线三星库仑编队相对运动方程为

(22)

式中，L1=m4l1+m5l2，L2=m5l1+m6l2，

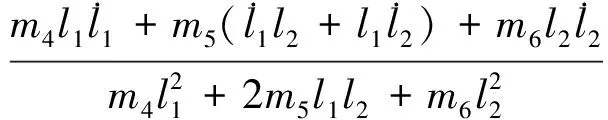
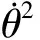
这里Q12、Q13、Q23为卫星间电荷乘积 ，即Q12=q1q2，Q13=q1q3，Q23=q2q3.本文均选取地球高轨道附近，上述式(22)为径向共线三星库仑编队在地球同步轨道处耦合的非线性常微分动力学方程.式(22)中卫星1与卫星2之间的距离l1、卫星2与卫星3之间的距离l2与滚转角θ和俯仰角ψ高度耦合，这使得可以通过控制卫星的电荷量来实现对卫星间距的直接控制和姿态角的间接控制，从而使系统渐进稳定.

2 共线三星库仑编队队形保持自适应控制

考虑到外界干扰力(如地球扰动力、太阳光压等)和库仑力静电场近似模型的不确定性，针对共线三星库仑编队构型保持设计了自适应控制律.

式(22)可简化为

(23)

考虑到在地球同步轨道处卫星会受到未知扰动力的影响，则式(23)可表示为

(24)

式中d为干扰项.

δX=X-Xd

(25)

速度误差为

(26)

不确定参数的估计误差为

(27)

复合误差可记为

(28)

对式(28)求导

(29)

令控制加速度控制律如下：

(30)

利用Lyapunov稳定性理论证明编队控制系统稳定性.定义Lyapunov函数为

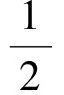
(31)

式中Γ为对角矩阵.

对式(31)求导：

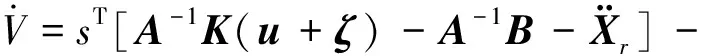
(32)

取自适应控制律为：

(33)

式中M=Kd.

将式(30)和(33)代入式(32)可得到：

(34)

3 数值仿真

本节应用Matlab/Simulink软件进行仿真校验.考虑卫星在编队飞行过程中受到的外界干扰力作用和卫星间静电场模型误差，对共线三星库仑编队在地球同步轨道上构型保持的自适应控制律进行仿真验证.

在地球同步轨道处，外部环境干扰力主要地球摄动和太阳光压产生，其相对干扰加速度选取为：d=[5.67×10-8sin(ωst) 3.34×10-8sin(ωst) 0 0][17].式中：ωs=Ω-ωB=(7.291×10-5-1.991×10-7) rad/s，ωB为地球绕太阳的旋转角速度[6].

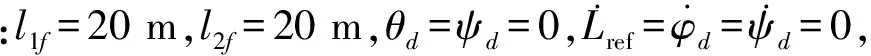
自适应控制参数设计为：

Λ=diag{10，0.1，0.01}，
Kp=diag{0.1，0.01，0.1}，
Γ=diag{1，0.1，1，0.1，0.01，0.1}.

仿真结果如图4～8所示，其中图4～5为卫星编队中各卫星的相对运动轨迹，在初始时刻卫星编队受到外界扰动力影响，其相对位置出现偏差，在4小时后卫星编队恢复原有构型；图6～7分别给出了在共线三星库仑编队自适应控制律的作用下，卫星间距和编队姿态角随时间的变化情况.在自适应控制律的控制下，约4h后，卫星间距离l12和l23分别收敛到40 m和30 m，面外俯仰角θ和面内偏航角ψ均收敛到0； 图8、图9分别给出了在自适应控制律的作用下，卫星间电荷乘积和卫星间作用力随时间的变化情况.在控制器作用过程中，卫星间电荷Q12与Q23为负值，Q13为正值，其数值先减小后增大最后分别收敛到-21.13 μC2、-18.72 μC2和33.24 μC2.仿真结果表明在共线三星库仑编队自适应控制律的作用下，编队构型能够达到期望构型，说明所设计的编队构型保持控制律是有效的.

4 结 论

本文研究了共线三星库仑卫星编队在地球同步轨道处相对运动动力学与控制问题.针对三星库仑编队模型的复杂性以及外界干扰和德拜效应的影响，提出了运用绳系编队的建模思想，来建立了共线三星库仑编队相对运动动力学模型的方法，并利用泰勒级数展开式对其进行线性化处理.本文设计了共线三星库仑编队自适应控制律，考虑到了未建模的扰动力，并通过数值仿真验证了其有效性.该方法也可用于其他类型的非接触力卫星编队在高轨的近距离航天任务.

[1] KING L B, PARKER G G, DESHMUKH S, et al.Spacecraft formation flying using inter-vehicle Coulomb force [R]. NASA/NIAC, 2002.

[2] ZHANG J R, YUAN C Q, JIANG D MI, et al.Adaptive terminal sliding mode control of electromagnetic spacecraft formation flying in near-earth orbits[J].Advances in Mechanical Engineering, 2014, 12(3):1-9.

[3] KING L B, PARKER G G, DESHMUKH S, et al.Study of interspacecraft coulomb forces and implications for formation flying[J].AIAA Journal of Propulsion and Power, 2003, 19(3):497-505.

[4] HARSH A.V. Four-craft virtual coulomb structure analysis for 1 to 3 dimensional geometries[D]. Virginia: Polytechnic Institute and State University, 2007.

[5] INAMPUDI R, SCHAUB H.Orbit radial dynamic analysis of two-craft coulomb formation at libration points[C]//AAS/AIAA Astrodynamics Specialist Conference. Washington D C: AIAA, 2010-7965.

[6] INAMPUDI R.Two-craft coulomb formation study about circular orbits and libration points[J].Ph.D. Thesis, University of Colorado, 2010, 16(7):37-42.

[7] WANG S,SCHAUB H.Nonlinear coulomb feedback control of a spinning two spacecraft virtual structure[C]//American Control Conference. Minneapolis, USA, 2006.

[8] HUANG J, MA G F.Nonlinear dynamics and reconfiguration control of two-satellite coulomb tether formation at libration points[J].Aerospace Science and Technology, 2014, 39(8):501-512.

[9] 张皓，师鹏，李保军，等.利用库仑力实现悬停轨道的新方法研究[J].宇航学报, 2011, 33(1):68-75.

ZHANG H, SHI P, LI B J, et.al. Hover orbit using inter-spacecraft coulomb forces[J]. Journal of Astronautics，2011, 33(1)：68-75.

[10] HUSSEIN I, SCHAUB H. Stability and control of relative equilibria for the three-spacecraft coulomb tether problem[J]. Acta Astronautica , 2009, 65(5-6):738-754.

[11] HUSSEIN I, HANSPETER S. Stability and control of relative equilibria for the three-spacecraft coulomb tether problem [C]//AAS/AIAA Astrodynamics Specialists Conference. Washington D C: AIAA , 2007, 64(4):19-23.

[12] ERIK A. HSCHAUB H..Collinear invariant shapes for three-craft coulomb formations.[J].Acta Astronautica, 2012, 72(10):78-89.

[13] HOGAN E, SCHAUB H. Linear stability and shape analysis of spinning three-craft coulomb formations. [C]//AAS Spaceflight Mechanics Meeting, 2011, 13(17):211-225.

[14] PETER D J, SCHAUB H. Out-of-plane stability of collinear spinning three-craft coulomb formations.[J].Acta Astronautica, 2009, 67(12):89-97.

[15] RUI Q K. MISRA A K. Dynamics of double-pyramid satellite formations interconnected by tethers and coulomb forces. [J].Acta Astronautica, 2016, 24(11):1265-1277.

[16] 王婷，张羽飞.等质量立体五星库仑编队飞行的分析与控制[J].宇航学报, 2015, 36(11):1279-1288.

WANG T, ZHANG Y F. Analysis and control for three dimensional five-satellite coulomb formation flight in geostationary earth orbit[J]. Journal of Astronautics，2015,36(11)：1279-1288.

[17] 徐增文,师鹏,赵育善.双电磁航天器编队构型保持自适应控制 [J]. 北京航空航天大学学报，2015，12(41):2302-2308.

XU Z W, SHI P, ZHAO Y S. Adaptive control for two-spacecraft electromagnetic formation keeping [J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 12(41): 2302-2308.

AdaptiveControlResearchofTwo-CraftCoulombFormationinTrackRadial

SHI Qiang, YUAN Changqing, SUN Yunlong， YU Haili

(AviationUniversityofAirForce,Changchun130022，China)

In this paper, the adaptive control problem of the collinear three-craft coulomb formation configuration keeping at geostationary orbit is investigated. The non-linear relative kinetic model of the collinear three-craft Coulomb formation in geosynchronous orbit is established, and the control strategy of only using the Coulomb force as the control force is studied to keep the radial static stability of the collinear three-craft Coulomb formation. Based on the non-linear dynamic model, considering the unmodeled disturbance force at space environment, the adaptive control law is designed. Finally, the numerical simulation is carried out.

coulomb formation； geostationary orbit； configuration keeping； adaptive control

*国家自然科学基金资助项目(11372353).

2017-09-17

V448.2

A

1674-1579(2017)06-0013-07

10.3969/j.issn.1674-1579.2017.06.003

施强(1993—)，男，硕士研究生，研究方向为卫星库仑力编队动力学与控制;袁长清(1974—)，男，教授，研究方向为航天器动力学与控制;孙云龙(1993—)，男，硕士研究生，研究方向为卫星库仑力编队动力学与控制;于海莉(1973—)，女，副研究馆员，研究方向为图书情报学.