基于Lyapunov最优反馈控制的月球中继卫星转移轨道设计

安 然，王 敏，梁新刚

(中国空间技术研究院通信卫星事业部,北京 100094)

基于Lyapunov最优反馈控制的月球中继卫星转移轨道设计

安 然，王 敏，梁新刚

(中国空间技术研究院通信卫星事业部,北京 100094)

随着电推进器及小推力转移变轨的研究逐渐深入，在深空探测领域应用电推力器是必然的发展趋势.文章基于以月球中继卫星的运行轨道地月L2点Halo轨道为目标轨道的轨道转移任务，采用Lyapunov最优反馈控制方法，计算单一轨道根数的局部最优控制率，通过遗传算法调整五个轨道根数的权重，得到时间最优的月球中继卫星小推力轨道转移方案，具有工程应用意义.

最优控制原理; Lyapunov最优反馈控制; 电推进; 小推力变轨; 不变流形

0 引 言

平动点是深空发展的研究基石，位于平动点附近的周期或拟周期轨道可为多种探测任务或中继通信任务提供良好的工作场所.在深空探测中，由平动点连接的不变流形可以为深空转移提供便利的“行星际高速公路”[1].地月L2的(拟)周期轨道是为位于月球背面的探测卫星提供通信中继的最佳场所，地—月L2点位于地月连线，并且一颗星可以实现对月球背面平均87.6%区域的覆盖.

在深空探测任务中，采用电推进器小推力发动机能够有效地提高探测器的有效载荷质量，但这也对转移轨道的设计与优化提出了新的挑战.由于深空探测的轨道要满足初始轨道及目标轨道的边界条件，推进器的推力恒定，推进器的俯仰角及偏航角可以作为控制量，使得小推力转移轨道的设计与优化问题可以归结为最优控制问题[2].

对于基于电推进的平动点轨道转移任务，需要借助三体模型下平动点轨道的不变流形.不变流形与平动点周期轨道紧密相连，它是一族空间轨道的集合，在空间中形成管状通道.不变流形分为稳定流形与不稳定流形，稳定流形上的质点会自发地趋近于周期轨道，所以利用稳定流形进行轨道转移可以节省燃料.通过利用地月L2点飞行轨道的不变流形，航天器在转移轨道中，只要进入不变流形即可以熄火，所以小推力转移弧段的末状态即为不变流形中任一点的位置与速度.

目前最优控制优化方法的主要为直接和间接算法[3]，而启发控制方法也同样可以应用在小推力转移轨道的优化上[4-5].这种方法的优点是收敛速度快.本文采取了启发控制算法中的Lyapunov控制算法，也称为Q-law算法.通过Lyapunov最优反馈控制将小推力转移优化问题转化成参数优化问题后，通过遗传算法优化小推力转移的5个权重即可得到时间最优的转移轨道.

1 不变流形设计及计算

由于小推力转移段的设计末状态在不变流形管道中，首先在限制性三体模型下对地月L2点Halo轨道的不变流形进行设计.不变流形与平动点周期轨道紧密相连，它是一族空间轨道的集合，在空间中形成管状通道.不变流形分为稳定流形与不稳定流形，稳定流形上的质点会自发地趋近于周期轨道[6]，所以利用稳定流形进行轨道转移可以节省燃料.将Halo轨道上任一不动点积分一个周期后得到的状态转移矩阵称为单值矩阵，通过计算单值矩阵中小于1的特征值对应的特征向量Vs，得到稳定流形[7]，不变流形表达式为

(1)

其中，d为设计参数，对于月球中继卫星，可取50 km[8].Halo轨道上的不动点通过相位角描述，每一不动点对应两条不变流形，Halo轨道所有不动点的稳定流形及组成了周期轨道的稳定流形管道.

圆形限制性三体模型的会合坐标系定义如下：原点O为两个大天体P1、P2的公共质心，OX轴在两个大天体P1、P2的连线上，且指向质量较小的天体一侧；OZ轴垂直于两天体的轨道平面，且与两天体系统角速度的方向一致；OY轴与OX轴、OZ轴构成右手系.其中P3代表飞行器，质量远远小于P1及P2的质量.

把会合坐标系中的不变流形转换到地球J2000惯性坐标系中.在位置转换时，首先求出飞行器在高精度会合坐标系下相对地球的位置，而后完成高精度星历会合坐标系向惯性坐标系旋转，最后将将归一化单位转化为国际单位制[9], 得到位置转换关系：

(2)

式中，x、y、z为飞行器在会合坐标系中的位置坐标，xi、yi、zi为飞行器在地球J2000惯性坐标系中的位置坐标；i、Ω、ω、θ分别代表月球在地球J2000坐标系下的实时轨道倾角、升交点赤经、近地点角距、真近点角.D为圆型限制性三体模型中会合坐标系的归一化长度单位，S为归一化地月实时距离.μ为月球相对地月系统的质量占比，λ为归一化单位下圆形限制性三体模型中L2点的位置.

计算速度转换时，需要考虑牵连速度及飞行器相对地球的相对速度，再完成坐标系旋转及单位转化，得到速度转换关系

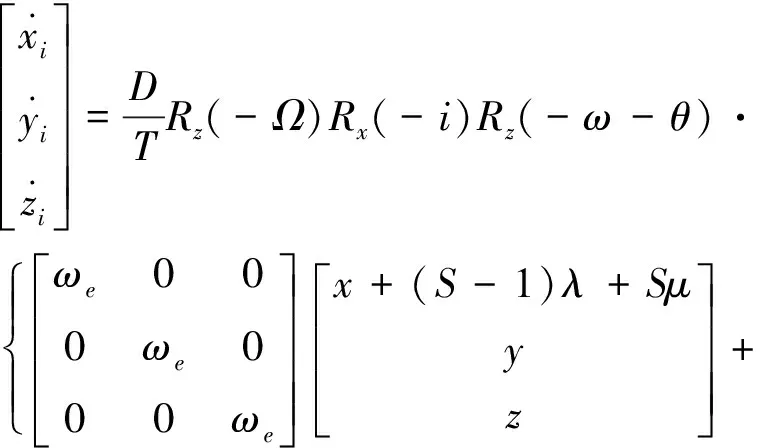
(3)

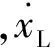
2 Lyapunov最优反馈控制率

2.1 动力学模型

在本文中考虑的动力学模型为轨道根数动力学模型，考虑月球引力摄动，小推力上升段的轨道动力学方程如下[10]：

(4)

式中，θ为真近点角，p=a(1-e2)为极轴，h为角动量，r=p/(1+ecosθ)，fr,ft,fn分别为中继卫星在径向、切向、法向上除地球引力的所受力的大小，在模型仅考虑月球摄动力的模型下，为中继卫星所受的月球引力与推力：

(5)

式中，α、β分别为中继卫星推力方向的俯仰角及偏航角，pr、pt、pn分别为月球引力在三方向的分量，月球位置通过高精度月球位置模拟计算得到.

2.2 针对单一轨道根数的局部最优控制率

在小推力转移段，通过Lyapunov最优反馈控制进行轨道优化设计.Lyapunov最优反馈控制率通过函数Q表示轨道状态与目标轨道的差值关系，即：

(6)

式中，ζ为5个轨道根数变量，分别为半长轴a，偏心率e，轨道倾角i，升交点赤经a，近地点角距ω，Wζ是 5个轨道根数的权重，权重要求是始终大于零的值.当飞行器轨道与目标轨道重合时，Lyapunov函数值将会等于零.h(ζ,ζT)为对特定轨道根数而言当前轨道根数值与目标轨道根数的差值计算，表示为

(7)

(8)

b为常数，可以取0.01.

(9)

ω的最大变化率只考虑平面内，或只考虑改变平面时的情况.可以求得5个轨道根数的最大变化率.对于半长轴：

(10)

偏心率:

(11)

轨道倾角:

(12)

升交点赤经:

(13)

平面内的近地点角距变化率:

(14)

其中：

(15)

对平面间的近地点角距：

(16)

2.3 控制策略

Lyapunov函数对时间的变化率为：

(17)

最优推力方向角α,β具有解析表达式，为了表示方便定义5个参数Ka,Ke,Ki,KΩ,Kω：

(18)

在Ka,Ke,Ki,KΩ,Kω5个参数中包含了Lyapunov函数中的5个权重.最优推力方向角α,β可以表示为：

(19)

(20)

(21)

通过上述方程可以将最优推力方向角转化成5个轨道根数的权重，即将Wa,We,Wi,WΩ,Wω作为控制变量，最优推力方向通过方程得出，既可以得到转移轨道所需时间及推进剂与控制变量的非线性关系.通过遗传算法进行非线性规划求解，可以得到使目标量最优的控制变量结果.

3 仿真分析

设月球中继卫星质量为2 000 kg，电推进系统的推力设为600 mN，即初始加速度为0.000 3 m/s2时，设定电推进器持续点火工作，选择不变流形相位角为160°时的不变流形，选择如下不变流形中的入口点作为电推进器的熄火点，熄火点的位置与速度为：

R=[1.273 9 0.232 0 0.202 7]×105km
v=[-615.3 1 466.9 586.2] m/s

熄火点的轨道根数为：

a=1.242 2×105km,e=0.155 9,i=23.78°,
Ω=349.515 7°,ω=141.389°,θ=241.163 7°.

为了减少中继卫星在小推力转移中的燃料消耗，选择一条轨道倾角及升交点赤经与熄火点所对应的轨道的轨道倾角及升交点赤经相同的规定，具体轨道根数如下：

i=23.78°,Ω=349.515 7°,ω=180°,θ=0°.

表1 最优权重Tab.1 Optimal scalar weights

小推力转移弧段的轨道半长轴、偏心率、轨道倾角及质量等状态量随时间变化如图4所示.

地球J2000坐标系下的轨道转移方案如图5所示：

图5中，绿色实线代表小推力转移轨道的初始轨道，蓝色实线为小推力转移弧段，红色虚线为地球惯性坐标系下的部分不变流形.

当推进装置采用化学推进器时，飞行器经过两次脉冲变轨进入不变流形，求解消耗燃料最少的转移方案，与采用电推进器的转移方案对比如表2所示：

表2 化学推进器与电推进器转移最优转移方案对比Tab.2 Comparison of optimal transfer design

4 结 论

本文针对位于地月L2点平动点飞行任务的转移轨道设计，通过最优控制原理中的Lyapunov最优反馈控制，求解小推力弧段的最优转移方案.得到飞行器质量为2 t时，从地球大椭圆轨道出发时的时间最优转移方案并给出中继卫星推力方向的俯仰角及偏航角随时间的变化关系，为获得工程上切实可用的月球中继卫星转移轨道提供了有益借鉴.

[1] 张泽旭，崔平远，崔祜涛．行星际高速公路技术[J] ．宇航学报，2007，28(1)：9-13.

ZHANG Z X, CUI P Y, CUI G T. Interplanetary superhighway technology[J].Journal of Astronautics, 2007，28(1)：9:14.

[2] SEUNGWON L, ANASTASSIOS P, PAUL V. A Low-thrust orbit transfer optimization with refined Q-law and multi-objective genetic algorithm[C]//AAS/AIAA Astrodynamics Specialists Conference. Washington D.C.:AIAA,2005.

[3] BETTS J T. Survey of numerical methods for trajectory optimization[J].Guidance, Control, and Dynamics, 1998, 21(2):193-207.

[4] PETROPOULOS A E.Simple control laws for low-thrust orbit transfers[C]//AAS/AIAA Astrodynamics Specialist Conference. Washington D.C.: AIAA, 2003.

[5] PETROPOULOS A E.Low-thrust orbit transfer using candidate lyapunov functions with a mechanism for coasting[C]//AIAA/AAS Astrodynamics Specialist Conference.Washington D.C.:AIAA, 2004.

[6] RODNEY L,ANDERSON,MARTIN W L.Role of invariant manifolds in low-thrust trajectory design[J] Journal of Guidance Control and Dynamics,2009,32(6): 1921-1930.

[7] DAVID C F, THOMAS A P. Earth-Moon libration point orbit stationkeeping: theory, modeling, and operations[J]. Acta Astronautica,2014,94(1):421-433.

[8] ZHOU J,XUE L,ZHOU F Q.Computations of low energy escaping/capturing trajectories in hill’s region via an extended poincaré map[J].Journal of Astronautics, 2007,28(3): 643-647.

[9] LEI H L,XU B. High-order solutions of invariant manifolds associated with libration point orbits in the elliptic restricted three-body system[J].Celestial Mechanics and Dynamical Astronomy,2013,117(4): 349-384.

[10] ANASTASSIONS E P. Refinements to the Q-law for low-thrust orbit transfers[C]// AAS 05-162, AAS/AIAA Space Flight Mechanics Conference.Washington D.C.:AIAA, 2005.

TransferTrajectoryDesignforLunarRelaySatelliteBasedonLyapunovOptimalFeedbackControl

AN Ran, WANG Min, LIANG Xingang

(InstituteofTelecommunicationSatellite,Beijing100094，China)

Electric thruster will play a more and more important role with the development of electric thrusters and low-thrust-based orbital transfer. The transfer trajectory optimal design is focused on for Lunar Relay Satellite, which works on the Halo orbit around translunar Libration point L2. Local optimal control for each of the orbit elements is calculated based on Lyapunov feedback control algorithm, and genetic algorithm is chosen to calculate the scalar weights for five orbit elements of transfer trajectory. The result shows the optimal control strategy of transfer trajectory for Lunar Relay Satellite has important engineering meaning.

optimal control theory; Lyapunov feedback control; electric thruster; low-thrust transfer trajectory; invariant manifolds

2017-03-19

V412.4+1

A

1674-1579(2017)06-0020-05

10.3969/j.issn.1674-1579.2017.06.004

安然(1993—)，女，硕士研究生，研究方向为航天器动力学；王敏(1978—)，男，研究员，研究方向为飞行器总体设计；梁新刚(1979—)，男，高级工程师，研究方向为航天器轨道设计与仿真.