CMGs驱动空间机械臂的自适应终端滑模控制
夏新会,冯 骁,贾英宏,徐世杰
(北京航空航天大学宇航学院,北京 100191)
CMGs驱动空间机械臂的自适应终端滑模控制
夏新会,冯 骁,贾英宏,徐世杰
(北京航空航天大学宇航学院,北京 100191)
针对V构型控制力矩陀螺(CMGs)驱动的空间机械臂的轨迹跟踪控制问题,研究一种自适应非奇异终端滑模(ANTSM)控制方法.利用基于Kane方程的递推组集算法建立了系统的动力学模型.以跟踪误差为变量,构造非奇异滑动面,以保证跟踪误差在滑动面上有限时间收敛.针对系统质量特性参数与关节处干扰力矩的不确定性,设计自适应控制器用以调节控制增益.该控制方法无需不确定性的上界,且闭环系统具有最终一致有界性.仿真结果表明,该控制器可使系统准确跟踪期望轨迹,并对质量特性参数不确定性和关节干扰力矩具有良好的鲁棒性.
自适应;终端滑模;空间机械臂;控制力矩陀螺;Kane方程
0 引 言
为增加航天器使用寿命,降低使用成本,空间在轨服务任务越来越受到重视[1-2],而空间机械臂系统是在轨服务的主要工具之一,为完成燃料加注、模块更换等空间操作,空间机械臂必须进行高精度轨迹跟踪控制.
传统的空间机械臂通常采用关节力矩驱动器作为执行机构.各关节处的作用力矩/反作用力矩直接作用于关节的外接体和内接体上,进而导致各运动体之间的动力学耦合十分显著,对系统高精度控制不利.为降低系统的动力学耦合,文献[3-6]中利用CMGs代替关节电机作为空间机械臂的执行机构,产生的控制力矩并非施加于关节处而是直接作用于运动体上,各关节可以自由运动,因而关节处不存在执行机构带来的作用力矩和反作用力矩,进而可大大减小机械臂与平台间的相互扰动,但文中所建立的模型均为耦合型模型,即在动力学方程中以显式形式直接给出各运动变量的耦合关系,这样直接导致仿真中的运算量与系统自由度数成三次方关系,因此计算效率很低.为此胡权等针对多体系统提出了一种基于Kane方程的新型的自动组集算法并应用[7-8].
为提高空间机械臂的性能,大批研究人员提出了针对不同任务和情况的控制算法.赵楠等[9]和贾英宏等[10]研究了基于三自由度球铰连接的机械臂系统的轨迹跟踪控制方法,但并没有考虑系统的不确定因素,如未知的外界扰动、惯量参数的不确定性以及非线性不确定性等.针对系统的不确定因素,滑模变结构控制因其鲁棒性强,且可使系统在参数摄动和外界扰动的影响下具有不变形的特点受到国内外学者的高度关注[11].然而传统的滑模控制具有容易产生颤振以及状态跟踪误差无限时间收敛的缺点,满志红等[12]首次提出一种MIMO的终端滑模控制器,于星火等[13]和冯勇等[14]对其作了改进,分别提出了快速终端滑模变结构控制和非奇异终端滑模控制,也有相当多的学者对自适应终端滑模控制进行了研究[15-17],但国内外针对CMGs驱动空间机械臂系统的控制研究尚不够充分,如文献[18]虽然对CMGs驱动机械臂的自适应滑模控制进行了研究,但却没有考虑系统的有限时间收敛问题.
因此本文以V构型CMGs驱动的空间机械臂为研究对象,考虑系统质量特性参数与关节处干扰力矩的不确定性,且该不确定性的上确界先验知识未知,将自适应律及终端滑模的相关成果结合起来对该系统进行高精度轨迹跟踪控制,完成了对闭环控制系统的仿真与分析.
1 系统描述
空间机械臂系统由卫星平台及多节臂杆构成,为降低运动体间的动力学耦合,每节机械臂上安装一对V字构型的CMGs作为执行机构,机械臂关节采用单自由度自由柱铰连接,文献[3]、[6]中已证实该设计可有效降低各运动体间的动力学耦合,而本文重点在于设计机械臂系统自适应滑模轨迹跟踪控制器,因此假定平台在惯性空间中的位置、姿态固定,CMGs驱动的机械臂系统如图1所示.将机械臂各臂杆由平台向外编号为B0,B1,…,Bn,其中B0为平台的编号,n为机械臂臂杆的数目.对系统中的运动体Bi(i=1,2,…,n),其内接绞编号为Ji,其内接体的编号为c(i),其上安装的CMGs的编号为ni.v构型CMGs中两个CMG的框架轴平行,均垂直于所在机械臂的旋转轴,并通过同步机构使两个框架角相同,进而使得CMGs的总角动量hi始终沿机械臂旋转铰链的转轴方向,如图2所示.
假定每个CMG的质心位置不随CMG绕其框架轴旋转而改变;此外因刚体Bi上的CMGs旋转引起的刚体Bi(含安装在Bi上的CMGs)的惯量力矩的变化很小.则空间机械臂系统可视为由n个运动刚体(含平台和铰链)组成的树形拓扑构型的多体系统,且每组CMGs均可认为是对应运动刚体中的一部分.
2 系统建模
2.1 坐标系的建立
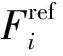
2.2 运动学与动力学
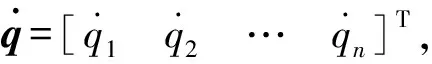

(1)
采用文献[7]的方法可得(1)中等号的左侧项,即
(2)
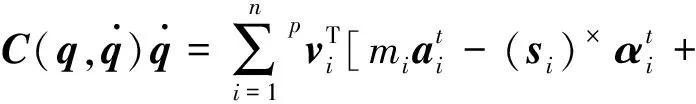
(3)
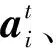
(4)
铰链运动学递推的递推公式为
(5)
采用文献[8]的方法可得(1)中等号右侧项中广义主动力的方程,即
(6)
(7)
至此,采用CMGs驱动的空间机械臂系统的系统模型已经得到.
3 非奇异终端滑模控制
考虑到系统质量特性参数与干扰力矩的不确定性,根据式(1)可得机械臂的动力学方程为

(8)


(9)
(10)
式中采用的范数均为向量的1-范数,δi(i=0,1,2)均为正常数.
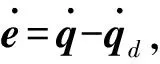
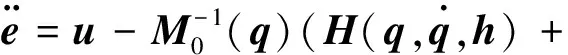
(11)
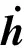
(12)
为设计系统的终端滑模控制器,首先需要选择恰当的终端滑动面,传统的终端滑模面(Terminal sliding mode, TSM)[19]为
(13)
式中:S=[s1s2…sn]T∈Rn,Λ∈Rn为常对角矩阵,λ为待设计的正常数,p和q为正奇数,且满足1 (14) 对式(14)两边对时间求导,可得 (15) 滑动面选定后,为满足到达条件,实现系统稳定,需要设计恰当的自适应滑模控制律 (16) 其中K=diag{k1,k2,…,kn}∈Rn×n(ki>0,i=1,2,…,n),系统的名义系统的等效控制ueq为 (17) 非线性反馈控制uN用于克服外界扰动与参数的不确定性,其方程为 (18) (19) (20) 但由于仿真过程中并不能保证滑动面始终为零,因式(20)中自适应参数的导数会大于零,进而导致式(20)中的自适应参数持续递增.为了避免这种情况,将式(20)中的自适应律作如下改进: (21) (22) 对式(22)求导,可以得到 (23) 根据式(11)、(15)~(21)可以得到 (24) 上述控制律中存在符号函数,在仿真过程中容易出现抖振,为避免这种情况,可用饱和函数代替符号函数,保证控制律的连续性,进而消除抖振[21]. 本节通过数值仿真验证自适应非奇异终端滑模控制器的稳定性,仿真任务是使机械臂系统能够准确跟踪指定轨迹.仿真中选用的模型是V构型CMGs驱动的平面机械臂系统,由三节臂杆通过单自由度自由柱铰连接而成,每节臂杆长1 m,其安装参数如表1所示,各自由柱铰均绕z轴旋转,(z轴指向纸面外),惯性参数如表2所示. 表1 安装参数Tab.1 Installation parameters 仿真过程中考虑系统质量的不确定性,假定每个臂杆的质量的不确定量为Δmi=3 kg(i=1,2,3),则每个臂杆质量的标称值为mi0=22 kg(i=1,2,3).假定机械臂系统所受的外干扰力矩是对应关节角速度的函数,即: (25) 给定关节角的期望轨迹为: (26) 表3 自适应律中的相关参数Tab.3 Parameters for the adaptation laws 图4为机械臂系统中各臂杆所受的外干扰力矩.各臂杆的关节角误差如图5所示,可见在考虑系统质量特性参数不确定性和系统外干扰以及不确定性上确界未知的情况时,系统仍能准确跟踪期望轨迹,且误差的收敛速度也比较快. 为了验证所设计的非奇异终端滑模面的有限时间收敛性,绘制滑模面随时间变化的曲线图,如图6所示,可见滑动面可在有限时间内到达平衡点,且收敛速度很快.自适应律(21)中的自适应参数如图7所示,可以看出自适应参数有界,不存在持续递增的情况.各臂杆CMGs的总角动量随时间的变化曲线如图8所示.图9与图10分别表示采用传统终端滑模面(13)与非奇异终端滑模面(14)所设计的控制器的控制输入,对比可见,当选用传统终端滑模面时,控制输入在第7 s时出现明显抖动,其根源就在于滑动面的奇异性,而选用非奇异终端滑模面则有效避免了这一问题. 本文研究了V构型CMGs驱动的空间机械臂系统在关节空间的轨迹跟踪控制问题.控制器的设计将非奇异终端滑模与改进的自适应律有效结合起来,形成了自适应非奇异终端滑模控制器.在设计过程中考虑系统质量特性参数与关节处干扰力矩的不确定性,且不确定性上确界的先验知识未知.通过闭环控制系统的数值仿真,验证了控制器的有效性. [1] FLORES-ABAD A, MA O, PHAM K, et al. A review of space robotics technologies for on-orbit serving[J]. Progressing in Aerospace Science, 2014, 68(8): 1-26. [2] 林兴来. 空间控制技术[M]. 北京: 中国宇航出版社, 1992: 25-42. [3] PECK M, PALUSZEK M, THOMAS S, et al. Control-moment gyroscopes for joint actuation: a new paradigm in space robotics[C]//1st Space Exploration Conference: Continuing the Voyage of Discovery, American Institute of Aeronautics and Astronautics Inc.,Orlando, 2005, 1: 204-233. [4] CARPENTER M D, PECK M A. Reducing base reactions with gyroscopic actuation of space-robotic systems[J]. Robotics, IEEE Transactions on, 2009, 25(6): 1262-1270. [5] BROWN D. Control moment gyros as space-robotics actuators[C]//AIAA Guidance, Navigation and Control Conference and Exhibit. Washington D.C.:AIAA,2008: 7271. [6] BROWN D, PECK M. Energetics of control moment gyroscopes as joint actuators[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(6): 1871-1883. [7] 胡权, 贾英宏, 徐世杰. 多体系统动力学Kane方法的改进[J]. 力学学报, 2001, 43(5): 968-972. HU Q, JIA Y H, XU S j. An improved Kane’s method for multibody dynamics[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(5):968-972. [8] 冯骁, 贾英宏, 徐世杰. 控制力矩陀螺驱动空间机器人的动量平衡控制[J]. 北京:北京航空航天大学学报, 2016. FENG X, JIA Y H, XU S J Momentum equalization control of space robot with control moment gyroscopes for joint actuation[J]. Beijing: Journal of Beijing University of Aeronautics and Astronautics, 2016. [9] ZHAO N, JIA Y H, XU S J. Trajectory tracking control of a reactionless space robot [J]. China Space Science &Technology, 2014, 34(2):13-21. [10] 贾英宏, 赵楠, 徐世杰. 控制力矩陀螺驱动的空间机器人轨迹跟踪控制[J]. 北京航空航天大学学报, 2014, 40(3): 285-292. JIA Y H, ZHAO N, XU S J. Trajectory tracking control of space robot actuated by control moment gyroscopes[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(3): 285-292. [11] 林壮. 欠驱动水平机械臂滑模变结构控制研究[D]. 哈尔滨: 哈尔滨工程大学, 2007. LIN Z. Sliding mode variable structure control for underactuated horizontal manipulators[D]. Harbin: Harbin Engineering University, 2007. [12] MAN Z H, PAPLINSKI A P, WU H R. A robust MIMO terminal sliding control scheme for rigid robotic manipulators[J]. Journal of Intelligent and Robotic Systems, 1994, 39(2): 2464-2469. [13] YU X H, MAN Z H. Fast terminal sliding mode control design for nonlinear dynamical system[J]. IEEE Transactions on Circuits and System-I: Fundamental Theory and Applications, 2002, 49(2): 261-263. [14] FENG Y, YU X H, MAN Z H. Non-singular terminal sliding mode control of rigid manipulators[J]. Automatica, 2002, 38(12): 2159-2167. [15] GAO D X, XUE D Y. Terminal sliding mode adaptive control for robotic manipulators[J]. World Congress on Intelligent Control & Automation, 2006, 2: 8853-8857. [16] NEILA M B R, TARAK D. Adaptive terminal sliding mode control for rigid robotic manipulators[J]. International Journal of Automation and computing, 2011, 8(2): 215-220. [17] MONDAL S, MAHANTA C. Adaptive second order terminal sliding mode controller for robotic manipulators[J]. Journal of the Franklin Institute, 2014, 351(4): 2356-2377. [18] JIA Y H, XU S J. Decentralized adaptive sliding mode control of a space robot actuated by control moment gyroscopes[J]. Chinese Journal of Aeronautics, 2016, 29(3): 688-703. [19] NOJAVANZADEH D, BADAMCHIZADEH M. Adaptive fractional-order non-singular fast terminal sliding mode control for robot manipulators[J]. Iet Control Theroy & Applications, 2016, 10(13): 1565-1572. [20] FENG Y, YU X, MAN Z. Non-singular terminal sliding mode control of rigid manipulators[J]. Automatica, 2002, 38(12): 2159-2167. [21] PARRA-VEGA V, HIRZINGER G. Chattering-free sliding mode control for a class of nonlinear mechanical systems[J]. International Journal of Robust & Nonlinear Control, 2001, 11(12): 1161-1178. AdaptiveTerminalSlidingModeControlofSpaceManipulatorsActuatedbyControlMomentGyroscopes XIA Xinhui, FENG Xiao, JIA Yinghong, XU Shijie (SchoolofAstronautics,BeijingUniversityofAeronauticsandAstronautics,Beijing100191,China) An adaptive non-singular terminal sliding mode (ANTSM) control method is proposed for trajectory tracking control of space manipulators actuated by scissored-pair control moment gyroscopes (CMGs). Equations of motion are derived by means of recursive algorithms based on Kane’s equations. The non-singular terminal sliding surface with the tracking error as the variable is constructed to ensure that the tracking error converges to zero in finite time on the sliding surface. The adaptive laws are also proposed for the control gain’s adjustment on account of the uncertainties of the system quality characteristic parameters and unknown disturbances. The control method does not need to know the upper bounds of the uncertainties and the closed loop system is uniformly ultimately bounded. Simulation results verify the effectiveness of the proposed controller combined with the accuracy of tracking expected trajectory and the robustness on the inertia parameter uncertainties and disturbance torque of joints. adaptive; terminal sliding; space manipulators; CMGs; Kane equation *国家自然科学基金资助项目(11272027). 2017-07-26 V448. 22+3 A 1674-1579(2017)06-0032-08 10.3969/j.issn.1674-1579.2017.06.006 夏新会(1992—),女,硕士研究生,研究方向为多体航天器动力学与控制;冯骁(1991—),男,博士研究生,研究方向为多体航天器动力学与控制;贾英宏(1976—),男,副教授,研究方向为空间机器人/多体系统动力学与控制、航天器姿态动力学与控制以及滑模控制;徐世杰(1951—),男,教授,研究方向为深空探测中的非线性轨道动力学与控制、航天器动力学与控制以及鲁棒控制理论与应用.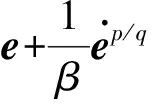

4 数值仿真与分析



5 结 论

