基于改进型遗传算法的共享汽车停放点布局优化研究

吴 阳，杨晓芳，郑 喆 WU Yang,YANG Xiaofang,ZHENG Zhe

（上海理工大学 管理学院，上海 200093）

·交通运输·

基于改进型遗传算法的共享汽车停放点布局优化研究

吴 阳，杨晓芳，郑 喆 WU Yang,YANG Xiaofang,ZHENG Zhe

（上海理工大学 管理学院，上海 200093）

随着共享汽车在大城市的发展日新月异，针对共享汽车停放点设置需要固定充电桩、必须有自己的固有停车位等问题，考虑共享汽车停放时的安全性和便捷性，在满足停放网点所能覆盖的合理范围前提下，以居民到达停放点的距离最短、设置停放点较少为目标函数，以停放点吸引范围、汽车行驶距离等作为约束条件，建立了共享汽车停放点位置布局的优化模型。由于模型多目标函数求解的相互矛盾，因此针对实际路网多向衔接的特点设计了改进型遗传算法，并采用MATLAB软件对样本区域进行优化求解。实例验证表明，假设城市中适合设置停放点有5×5个节点作为备选，计算约100次后趋于平稳，获得有效解，多目标规划的两个目标函数的适应度值分别681.6km为和8个目标点，当节点较少时，获得的运算速度相对较优。

城市运输；共享汽车；遗传算法；停放点；优化研究

0 引言

近几年共享单车发展迅速，而共享单车的“升级产品”共享汽车，也开始投入到城市日常交通之中。如果说共享单车很好地解决了最后“一公里”的出行问题，那么共享汽车可以覆盖更为广泛的范围，按60分钟的车程计算，共享汽车的出行范围大多可以覆盖一个大型城市的绝大部分范围。但是，目前而言共享汽车的推广和使用，远无法和共享单车相比较。其停车资源的受限性制约着共享汽车平台的发展。目前而言，在大城市、中心城区的停车位本身就十分紧张，若还要单独为“共享汽车”再划分出一定量的停车区，明显是难以实现的。

国内外对共享汽车停放点位置选择的研究不多，更多的研究中心放在了管理理论或管理政策上。王新源、赵斯惠、朱学杰等分析了共享经济活动和商业模型的高速发展，讨论了共享汽车运营的可行性，并提出了创新性运营策略，最后提出通过与公共汽车公司、汽车租赁公司的合作，整合或改建已有停车场站增加共享汽车停放点[1-3]。伏梅娟通过模拟的实验方法测试消费者对于汽车共享的动机强度、认知评价、情绪体验和消费意愿，同时测量了消费者动机强度、行为评价和情绪体验的中介作用[4]。程苑、鞠鹏等通过分析私家车与汽车共享的影响、博弈过程，并研究汽车共享项目的引进和政策的制定，得出引导出行者选择共享汽车出行方式的方法[5-6]。且丽莎研究了汽车共享中的空车调配问题，以运输总收益最大为目标，根据用户需求分布情况和网点车辆等数据，确定每时段各车辆的调配和运送情况，以求获得经济效益的最大化[7]。夏凯旋、何明升等以减少交通流量，减少大气污染，提高交通时效为研究对象，对共享汽车服务质量模型进行了评价分析[8]。王丽敏和杨帆等分别通过定性和定量的手段，研究了影响站点选址的因素、方法和原则，并确定各评价指标的权重。运用模糊综合评价法建立了相应站点选址方案评价模型[9-10]。相对来说，电动汽车充电桩布局设置的研究时间较长，研究成果也较多，但由于共享汽车停放点的布局，不同于电动汽车充电桩的布局设置，所以充电桩的布局优化研究，更多的是具有指导意义和参考价值。熊虎等采用排队论M/M/S模型，结合改进粒子群优化算法，以电动汽车排队等候时间为标准确定充电站规模和布局情况[11]。郑陈权针对用户的充电行为和充电方式的选择，构建点需求和路径需求两种需求模型，使用蚁群算法求解出充电桩选址规划方案[12]。王露则采用改进型遗传算法，以投资最小为目标函数，建立并求解充电设施布局选址优化模型[13]。

国外对共享汽车的研究较早，Alvina G.H.Kek等研究了汽车共享多个停车场之间的车辆调配问题，以总费用最小为模型目标，建立三阶段最优化理论模型[14]。Jory Firnkorn探讨了Car to go对于减少私家车的作用，通过调查数据分析，得出电动汽车的投入使用减少了居民的购买汽车的意愿[15]。Meijkamp RG从成本—收益角度分析发现，很多私家车使用率并不高，但又不能没有，而通过汽车共享就可以解决矛盾、减少固定费用。用户接受汽车共享服务的主要动机是从经济角度考虑，并可极大降低出行拥挤度[16]。Matthew Barth等通过建立多网点汽车共享服务的仿真模型，详细评估了汽车共享服务车辆的分配、具体使用情况等，并通过例证表明该系统的决策与服务车辆和出行次数的比值有紧密联系[17]。

现有的文献对共享汽车停放点设置的研究还比较少，且仅有的相关研究更多是定性的理论研究或是较为简单的评价、比较模型。本文参考研究相对成熟的电动汽车充电桩的布局规划[18-19]，建立优化模型。

本文主要就停放点的整体布局建立优化模型，以居民到达停放点的距离最短、设置停放点较少为目标函数，以停放点吸引范围、汽车行驶距离等作为约束条件，对一个区域的停放点位置进行布局和优化。

1 模型设计

1.1 参数说明

假设区域内有若干主要交通流的节点，节点的集合记为A=Ai｛｝，其中i=1,2,…,j,…,n，记Lij为节点Ai和Aj之间的距离，如图1所示。对任意节点Ai有属性其中和分别表示区域Ai到区域Aj选择共享汽车出行的居民出行量和区域Aj到区域Ai的出行量，ri为区域Ai吸引范围的半径，吸引半径的大小和区域出行量有关。Pi为该节点Ai内是否设置共享汽车停放点的情况，其中Pi=｛0,1｝，若Pi=0表示该区域不设置停放点；若Pi=1表示该区域设置停放点。

图1 区域内停车区基本参数设计

为了减少计算量和模型建立的简洁，做如下定义：

定义1：吸引范围的划分大小合适，过小则造成计算和建模与实际出现较大误差；过大则导致计算量过大。在文中，假设区域内居民都集中在节点位置（或可通过共享单车等其他出行方式集中到节点处），即节点所在区域内部的居民走行距离忽略不计，有Lii=0；同理，节点对本身的吸引量；

定义2：由于共享汽车主要针对中短途出行，结合实际情况，定义共享汽车单次行驶距离最大为S（单位km） （S在后文算例中取值200）；

定义3：居民出行选择最短径路。虽然城市交通现状是当交通拥堵时，居民为了节省时间，往往选择绕行等方式避开拥堵区域，但是为了研究方便，设定所有出行均按最短路行驶，记为Lij=min Lij（）；

定义4：对每一个停放点，不考虑停放点的容量和配车数量，即认为只要有停放点就可以使用或停放共享车辆，且汽车均保证电量充足状态。

1.2 目标函数

一般而言，城市居民出行方式的选择中，除了散步和运动外，绝大多数时候是选择步行距离较短的出行方式。同时考虑城市交通的实际情况，需考虑引入以下几个目标函数：

（1）各个节点吸引区域的居民到共享汽车停放点之间的总走行距离最短。共享汽车主要用于中短途的运输，能缓解日常交通压力，便于居民出行，但是如果居民前往停放点的距离过远，则达不到共享汽车便民出行的。因此要尽可能的使居民出行或到达目的地后步行的距离最短。

（2）设置的停放点数量合适。过少的话导致居民取用不便，又不能起到“共享”的作用，但过多的设置停放点会导致道路的压力过大，尤其是使用共享汽车的城市多为较为繁华的大型城市，交通较为拥堵。因此，设计的停放点数量和位置，应该是在保障目标函数（1）后，减少停放点设置，这才能使共享汽车的停放最为合理，使用最为方便。

1.3 约束条件

与共享单车停放较为随意不同，共享汽车需要设计有一定面积、一定设施的固定停放点，因此其约束条件更为严格，主要体现在以下几点：

（1）由于目标函数中即希望设置的停放点即不能过多而影响道路交通条件，又需要保证一定数量，避免居民出行使用不便，因此使用约束条件选择合理的停放点数量，如果居民所在节点没有设置停放点，则去往相邻节点，考虑步行或共享单车等其它方式在节点间的衔接情况，设计居民在任意一端的走行距离不超过a（单位km） （a值后文取值为2），既总行走距离不超过2a：

其中：节点m、n为停放点，i、j为居民起讫点，若起讫点就为停放点，此时Lim变为Lii，即取值为0。

（2）行驶距离约束。单车的行驶距离不超过S（km），城市居民出行一般只会开行一次共享汽车，则对于任意两联通的节点间的最大距离有约束：

（3）节点吸引范围，也可以认为是居民选择共享汽车出行时，所能接受的停放点所在的范围，即范围内有停放点则选择共享汽车出行，否则选择其他的出行方式，因此有：

（4） 其他约束限制。

根据上文分析，构建共享汽车停放点布局优化模型如下：

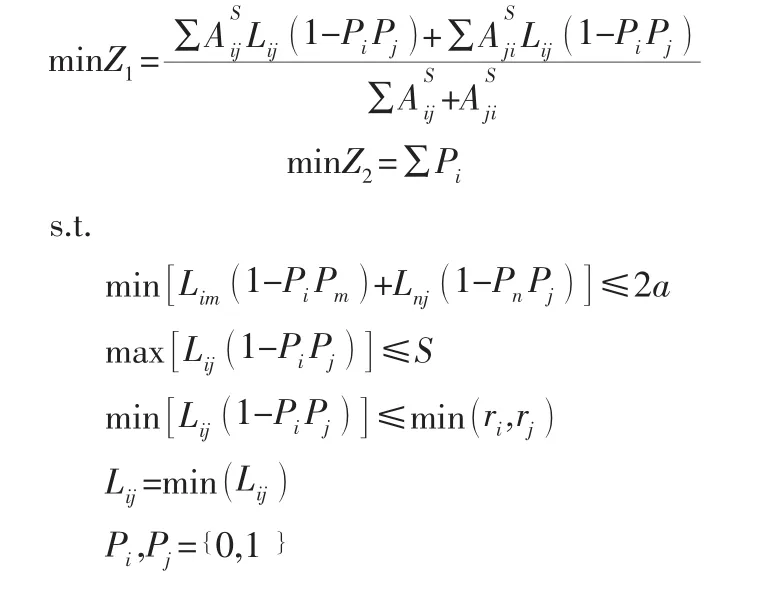
2 优化算法设计

由于上述问题是多目标优化问题，对多个子目标同时进行优化，每个子目标函数都较为复杂且子目标之间并非正相关，很难找到一组解，能同时使得各个子目标同时达到最优，通常只能求得模型的非劣解，即Pareto最优解。

本文采用改进型遗传算法进行求解。遗传算法是一类借鉴生物界适者生存，优胜劣汰等进化规律演化而来的随机化搜索方法。遗传算法为优化算法中的一种基本算法，在解决节点较多、规模较大的模型中，能较快的获得满意解。

遗传算法是模拟达尔文生物进化“适者生存”的思想，借用生物遗传学的若干概念（如染色体、基因、种群、复制、交配、变异、父代、子代、适应性等），模拟自然选择和生物遗传过程而提出并发展起来的一种运用于大规模组合优化问题的随机搜索算法。在进行遗传操作时，几个重要的参数为：染色体长度L，种群大小M，交叉概率Pc，变异概率Pm，终止代数T。

2.1 改进型遗传算法设计

由于使用遗传算法求解时，使用简单染色体不能很好地表示出节点之间的联系。同时，由于两个目标函数之间存在矛盾关系，式（1）希望有越多的停放点越好，而式（2）则希望越少越好。求解此时的多目标优化问题，如果仍然采用遗传算法，会出现以下问题：

①多目标遗传算法的局部搜索能力较差；

②最优解的收敛速度慢，甚至难以到达最优解的区域；

③由于参数复杂度高，导致运算速度下降。

因此要对遗传算法的编码方式、交叉变异运算和适应度值计算三方面进行改进型的设计和计算。

（1）遗传算法编码方式

一般来说，运用遗传算法解决优化问题时，一般会将该问题的解编码为一个具有某种设计规则的自然数组。由于城市道路横纵向的连接，二维的编码更符合实际情况的设计，本文采用改进型遗传算法编码向量，设计初始染色体为矩阵C，有C作为一个染色体来表示一个方案的各种属性，其中，染色体中的每个基因片段Pij都对应一个停放点的方案。对任意基因片段Pij有Pij=0,（）1 ，其中 1≤i≤m，1≤j≤n。

（2） 适应度函数

城市道路的实际情况中，往往有些道路实际上是不连通的，为了表达这类道路情况，引入适应度函数，即惩罚函数。个体适应度主要由目标函数值决定，在本文中，计算染色体适应度值时，对于超出限制或不能实现的部分基因值，引入惩罚系数+∞，以及阶跃函数J（x），其定义为：

将惩罚函数并入目标函数，即：

（3） 选择方式

本文采取“精英保留”的选择策略，需要根据不同初始方案得出停放点最优设置，相对更优的个体直接进入子代，再对当前种群执行随机遍历抽样，直至子代种群规模与父代相同。

（4） 交叉与变异方式

同时，变异运算改进为随机选择区域内的一个基因值进行变异，若随机选择为Pii，则变异后仍然有Pii=0；若随机选择为Pij且i≠j，则变异时进行0-1变换。

（5）目标函数的冲突度计算及目标函数变换

由于两个目标函数之间的矛盾关系，容易导致该多目标优化问题找不到最优解，因此引入粗糙集方法，用冲突度大小来衡量目标函数中最好的“折中解”。并通过加权法重新确定目标函数值，即适应度值的大小[20]。

记多目标优化问题的理想解集为：

其中：f1（C ），f2（C）分别为两个决策目标函数；C表示各停放点设置方案，记C=（Pij）T；Pij各停放点设置方案中的决策变量。

其中：决策函数的任意解C∈X，X表示所有可行方案组成的解集。

假设对第k个目标函数fk（C ），有为fk（C ）的最优解；有为fk（C ）的可行解。则可行解有对于目标函数fk（C）的满意度值为：

当存在解时Cl∈X，同时Cl既不是fk1也不是fk2的最优解，根据式（11） 可获得和，定义此时的目标函数fk1和fk2的冲突度值为：

在此基础上就可将原多个目标函数转换为一个目标函数，如式（10）转化为：

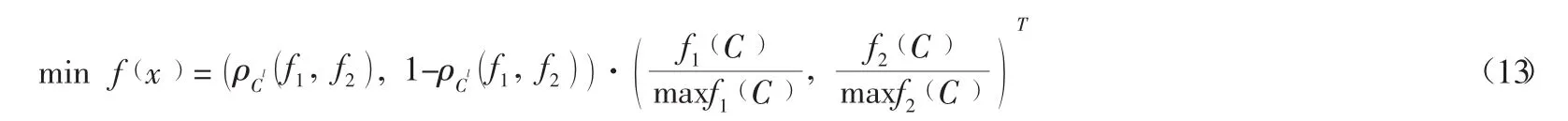
值得注意的是，当Cl为不同可行解的时候，式（13） 中改进后的单目标函数的系数不同，导致minf（x）取值不同，因此使用改进遗传算法进行可行解的搜索时，要尽可能的覆盖可行解集中的所有解，最终转化后的目标函数才能更趋于满意解。

2.2 算法步骤

Step1初始化设计：设置代数计数器，初始代数t=0，设置最大进化代数T，随机生成个体作为父代群体。

Step2个体评价：计算初始父代群体中个体的目标函数，即适应度值。

Step3选择运算：将选择算子作用于群体。选择的目的是把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。选择操作是建立在群体中个体的适应度评估基础上的。

Step4交叉运算：将交叉算子作用于群体。遗传算法中的核心作用的就是交叉算子，用于生成子代个体。

Step5变异运算：将变异算子作用于群体。即是对群体中的个体串的某些基因座上的基因值作变动，用于生成新子代。

群体代数P（t）经过选择、交叉、变异运算之后得到下一代群体P（ t+1）。

Step6终止条件判断：当遗传代数t为最大进化代数，即t=T时，则以进化过程中所得到的具有最大适应度个体作为最优解输出，终止计算。此时最优的停放点布置方案即可认为是该综合优化的Pareto最优解。

3 算例验证

假设城市中适合设置停放点有5×5个节点作为备选，为节点（1） 至（25）。城市路网图如图2所示，图中数字表示路段Lij的距离，节点边括号中的数字分别表示该节点的吸引范围，为了减少计算量，设各个节点之间的吸引量为一个相同的定值，在此设为1。

图2 路网节点示意图

根据式（13），将改进后的目标函数值作为适应度值，随机选择两个初始解集作为父代进行改进型遗传算法的计算。确定此时f1的最优解为25个节点全部设置停放点；f2的最优解为在25个节点处均不设置停放点。则两个目标函数的最优解分别为f1（C25）=0和f2C8（）=0。改进模型的极大值分别为max f1=Σmin Lij（）=25×24×2.1=1 260km和max f2=ΣPi=25。

按前文所述模型，经试算、调整，最终确定算法各个参数值为：最大进化代数T=1 000，交叉概率pc=0.75，变异概率pm=0.05。整个求解过程基于Matlab软件运行，约计算100次后趋于平稳，最终获得理想解此时综合目标函数min f（）C=0.3767，多目标规划的两个目标函数的适应度值分别为：minZ1=681.6km和minZ2=8个。目标函数迭代变化图如图3所示。

图3 目标函数迭代变化图

可以看出，改进型遗传算法的可行解中，当节点较少时，获得的改进型目标函数相对较优。同时，通过简化节点吸引量和发生量之后，计算时间和计算量都大大减少。总体来说，使用改进型遗传算法计算共享汽车停放点布局优化问题时，其计算结果比较令人满意，也满足约束条件，获得的方案合理，计算时间也令人满意。

4 结 论

目前而言，城市中共享汽车的种类大部分为电动汽车和新能源汽车，而这些汽车的选址需要合理的布设充电桩、维护设施和停放点作为支撑，在共享汽车投入使用之前还需考虑对周边交通影响等情况。因此，所设计的优化模型目标函数和约束条件众多，一般的数学方法难以直接求解。本文采用改进型遗传算法，更形象合理地描述道路和停放节点的实际情况；引入冲突度的概念，在将多目标规划简化为单目标规划时，尽可能地避免主观系数的影响。通过算例验证，改进型的遗传算法在解决小规模区域共享汽车停放点布局优化的问题上，取得不错的计算速度和计算结果，证实该研究方法可以应用于小规模区域下的电动汽车共享站点实际规划。但是，在大规模城市的优化模型应用，以及考虑随机性的出行、停放情况下共享汽车的停放点优化布局问题，还有待进一步的学习和研究。

[1]王新源.北京市发展共享汽车服务的运营策略研究[J].时代金融，2014(2):123-124.

[2]赵斯惠.基于O2O视角的共享经济商业模式研究——以汽车共享为例[D].北京：首都经济贸易大学（硕士学位论文），2015.

[3]朱学杰.国内汽车共享行业发展现状及趋势探讨[J].科技创新与应用，2016(29):75-76.

[4]伏梅娟.目标信息框架下汽车共享消费意愿的影响研究——调节定向理论视角[D].南京：南京工业大学（硕士学位论文），2015.

[5]程苑.汽车共享下的城市交通出行方式博弈研究[D].哈尔滨：哈尔滨工业大学（硕士学位论文），2015.

[6]鞠鹏，周晶，陈星光,等.考虑汽车共享的出行方式选择的演化博弈分析[J].管理现代化，2017(1):70-72.

[7]且丽莎.基于“汽车共享”的空车调配问题研究[D].成都：西南交通大学（硕士学位论文），2010.

[8]夏凯旋，何明升.汽车共享服务创新及其服务质量评价模型[J].甘肃社会科学，2008(1):206-210.

[9]Edourad Serot，杨帆.电动汽车共享服务选址方法研究[J].上海汽车，2013(7):32-35,39.

[10]王丽敏.基于AHP和模糊综合评价法在共享汽车站点选址的研究[J].江苏科技信息，2013(7):60-62.

[11]熊虎，向铁元，祝勇刚,等.电动汽车公共充电站布局的最优规划[J].电力系统自动化，2012(23):65-70.

[12]郑陈权.城市电动汽车充电设施最优选址研究[D].南昌：南昌大学（硕士学位论文），2016.

[13]王露.城市纯电动汽车快速充电设施的布局选址优化模型研究[D].北京：北京交通大学（硕士学位论文），2016.

[14]Alvina G.H.,Ruey Long Cheu,Qiang Meng,et al.A decision support system for vehicle relocation operations in carshing systems[J].Transportation Research,2008(13):13-20.

[15]Jory Firnkorn,Martin Muller.Free-floating electric cars haring-fleets in smart cities:The dawning of a post-private car era in urban environments?[J].Science Direct,2015(45):30-40.

[16]Meijkamp RG.Changing consumer behavior through Eco-efficient Services:An empirical study on Car Sharing in the Netherlands[M].PhD dissertation Delft University of Technology,2000:61-62.

[17]Matthew Barth,Michael Todd.Simulation model performance analysis of a multiple station shared vehicle system[J].Transportation Research,1999(7):237-259.

[18]李菁华，张峥，方达,等.基于混合差分蜂群算法的城市电动汽车充电站布局规划[J].东北电力大学学报，2016(4):84-90.

[19]谭洋洋，杨洪耕，徐方维,等.电动汽车充电站规划方案的模糊物元评估方法[J].电力建设，2016(9):36-42.

[20]邓方安.多目标优化中目标函数间冲突问题研究[C]//中国rough集与软计算学术研讨会，2004.

Research on Parking Spots Optimization of Car Sharing Based on Improved Genetic Algorithms

(Management School,University of Shanghai for Science and Technology,Shanghai 200093,China)

With the rapid development of shared cars in big cities,the need for fixed parking pits for shared car parking points must have their own inherent parking spaces and other issues,consider sharing the safety and convenience of car parking.Covering the reasonable range of the premise of the residents to reach the parking point of the shortest distance,set the parking point less as the objective function to the parking point range,car travel distance as a constraint,the establishment of a shared car parking point location optimization model.Because of the contradiction between the multi-objective function of the model,an improved genetic algorithm is designed for the multi-directional convergence of the actual road network,and the sample region is optimized by MATLAB software.The example shows that the fitness value of the two objective functions is 681.6km,which is the ideal value of the effective solution and the multiobjective programming,assuming that the parking point in the city is 5×5 nodes as an alternative.And 8 target points,when the node is less,the obtained operation speed is relatively better.

urban transportation;car sharing;genetic algorithm;parking point;optimization research

F570

A

1002-3100(2017)12-0078-06

2017-10-12

国家自然科学基金资助项目，项目编号：51308409；上海市浦江人才计划资助项目，项目编号：15PJC075。

吴 阳（1991-），男，湖北随州人，上海理工大学管理学院硕士研究生，研究方向：智能交通、驾驶行为；杨晓芳（1975-），女，山西新绛人，上海理工大学管理学院，副教授，博士，研究方向：智能交通、驾驶行为；郑 喆（1993-），男，黑龙江佳木斯人，上海理工大学管理学院硕士研究生，研究方向：交通运输规划。