组合追溯信息赋码的矩阵模型研究

阳晓慧，郭炳晖，殷子樵，杨小博

（北京航空航天大学 数学与系统科学学院、数学信息与行为教育部重点实验室，北京 100191）

组合追溯信息赋码的矩阵模型研究

阳晓慧，郭炳晖，殷子樵，杨小博

（北京航空航天大学 数学与系统科学学院、数学信息与行为教育部重点实验室，北京 100191）

随着我国经济模式与消费结构的不断升级，全社会对食品安全和追溯系统的关注日益提升。文章面向酒类产品信息追溯系统中在生产流通环节需要对产品追溯信息进行重新包装编码的问题，在构建酒类产品追溯赋码体系的基础上，提出了基于临阶包装矩阵和非临阶包装矩阵的组合追溯信息赋码描述模型，并给出了相应的低阶包装重组对应的组合赋码流程。

追溯信息；组合赋码；矩阵模型

0 引言

随着我国经济的不断发展和人民生活水平的不断提高，关系到全民健康的食品安全问题越来越受到全社会的共同关注。特别是在无线射频识别技术和电子产品编码技术等物联网相关领域的科学创新背景下，建立食品类产品新消息追溯系统被认为是能够控制食品安全、实现产品防伪和解决商品流通秩序混乱等问题的最有效手段。由于信息追溯是对每件产品的信息建立一个独立的电子档案以实现对商品信息的追溯管理，所以能够实现将产品加工、生产和流通等环节的信息聚合溯源的功能。

食品信息追溯系统主要依托于电子标签和数据库系统构建，分为企业自建和政府导向两类。目前国内在农产品、乳制品、酒类等方面已经有了一定的研发和应用。何晓艳综合分析了影响和制约我国农产品质量追溯体系建立的核心问题[1]；陈佳伟等对农产品追溯模式进行探讨并构建了基于物联网的农产品供应链追溯体系[2]；武尔维等研究了在移动互联网环境下基于Android智能终端的农产品安全追溯系统架构[3]；廖祎玮等提出了基于物理层、汇聚层、服务层三个层次的物联网信息追溯系统构建模型[4]；郑火国等综述了如何构建面向农产品的食品安全追溯链[5]。上述研究都从理论研究的角度做出了对信息追溯系统建设的探索。

本文以酒类产品的信息追溯系统建设为背景，针对在生产流通环节中对产品追溯信息进行重新包装编码的实际问题，在构建酒类产品追溯赋码体系的基础上，提出了基于临阶包装矩阵和非临阶包装矩阵的组合追溯信息赋码描述模型来描述生产过程中多层包装的问题，通过矩阵的操作来刻画产品改变包装的变化操作。

1 面向酒类产品的信息追溯系统

一般而言，面向酒类产品的信息追溯系统可以分为三个不同的层次：采集服务端、服务访问层和客户端（如图1所示）。在单间酒类产品上赋码的追溯信息编码在这样三个层次的数据系统中不断添加环节信息，最终形成一条完整的信息溯源链。

图1 面向酒类产品的信息追溯系统

对于酒类生产企业，产品信息追溯的过程一般需要以下步骤：根据企业需求设计标签样式→基于标签样式研发商品唯一识别码→建立识别码分布式存储数据库和网络电子仓库站点→基于信息盲采集技术集成标准化手持式电子标签扫描、记录和传输系统→建立智能标签识别码智能管理系统→设计识别信息数据压缩索引查询系统→研发基于追溯数据大数据的企业及消费者第三方信息标签设计规则和服务客户端。在上述流程中，如何能够在单间酒类产品重新包装时根据原有追溯信息产生出新的大包装编码，一直以来都是影响企业产品归集重组效率的关键问题。

本文针对这一关键问题，通过将生产线条码采集流程中不同包装层级进行数学建模来解决重新包装后的追溯信息赋码问题。生产线条码采集流程涉及到了重新包装的重新赋码环节（如图2所示）。

图2 生产线条码采集流程图

以一般酒类商品的包装层级依次是箱、剁、批次为例，整个生产线条码采集具体步骤如下：（1）开启系统，登录条码采集子系统；（2）获取生产计划信息，一般来说是生产包装线的生产订单信息；（3）设置参数、调机：工作人员根据生产计划单信息，补充设置一些参数，如：生产班组、记账时间、批次等信息。调机主要是调整条码采集设备的位置，以便采集不同产品包装物上的条码信息；（4）垛码机箱计数采集：采集码垛机入口处的计数值，作为采集码垛箱数；（5）条码采集：采集商品的箱条码信息；（6）条码采集数量与码垛机的计数数量的一致性校验。不一致时，用虚拟箱条码补齐条码数量；（7）码垛数量校验：箱条码采集数量（以计数值为准）达到预设托板码垛数量时，系统自动生成一个虚拟托板编号，并生成箱、垛对应关系，实时上传系统；（8）生产计划完成，且所生产的产品均已完成相应的入库，则系统自动生成相应的生产订单的生产、入库信息报表，提交销售管理系统。在采集过程中，由单件产品组合成更高层级的包装时，生产线的工作人员会将组合产品的唯一识别追溯码赋到新的包装上。

2 追溯信息重新组合赋码的矩阵模型

2.1 不同层级的包装定义

针对生产线流程中产品更换包装、更换批次、整体归集等实际生产需求带来的追溯信息编码重新赋值问题，本文提出以单件产品追溯信息为元素使用邻接矩阵来刻画包装操作的模型，通过标准化的理论模型来解决复杂的多层包装重新赋码问题。

首先，定义包装的阶。若某一级包装为阶包装，且该级包装直接合并装入更大一级的包装内，则更大一级的包装定义为n+1阶包装。规定原始产品为第0阶包装。为了说明该定义，我们不妨以酒业生产线为例。在该生产线中，单瓶的酒为原始产品，故单瓶的酒为第0阶包装；多瓶酒封入统一包装箱内，成箱贩卖，则箱为1阶包装；在运送途中，多箱酒并为一垛，则垛为2阶包装，以此类推。

进一步，定义邻阶包装。若两个不同阶的包装，阶数相差为1，则称此两阶包装为邻阶包装；否则，称为非邻阶包装。若两阶包装为邻阶包装，则其中阶数较小的包装称为低阶包装，阶数较大的包装称为高阶包装。从定义中不难看出，只有具有直接包装关系的两阶包装才可以称为邻阶包装，比如酒与箱、箱与垛；而具有间接包装关系的两阶包装则称为非邻阶包装，比如酒与垛。

2.2 邻阶包装的矩阵表示

对于邻阶包装的概念，可以直接运用复杂网络学科中经常用于表示从属关系的二模网络（2-mode network）中的相关概念来描述，进而定义邻阶包装矩阵。设两阶包装为邻阶包装，其中低阶包装共有m个，高阶包装共有n个（n≤ m ），称m×n阶矩阵A为邻阶包装矩阵，若Aij满足：当第i个（1≤i≤ m ）低阶包装被封入了第j个（1≤j≤ n ）高阶包装时，Aij=1；否则，Aij=0。

由产品包装的一些原则，我们不难得出邻阶包装矩阵应具有如下性质：

（1）由于每一个低阶包装只能装在一个高阶包装中，所以矩阵中，每一行至多有一个1；

（2）设每个高阶包装中至多可以装载m个低阶包装，则邻阶包装矩阵的每一列至多有m个1。

2.3 非邻阶包装的矩阵表示

直观而言，非邻阶包装关系是由多阶邻阶包装连接而成的。非邻阶包装矩阵应该可以由多阶邻阶包装矩阵计算得出，并且应满足与邻阶矩阵相似的性质：若某一阶包装被封入了它的某一阶非邻阶包装中，则此两阶包装的非邻阶包装矩阵中对应位置应为1；否则，该位置为0。由此可以定义非邻阶包装矩阵。设两阶包装为非邻阶包装，其中阶数较低的包装共有m个，阶数较高的包装共有n个（n≤ m ），称m×n阶矩阵A为非邻阶包装矩阵，若Aij满足：当第i个（1≤i≤ m ）阶数较低的包装被封入了第 j个（1≤j≤ n ）阶数较高的包装时，Aij=1；否则，Aij=0。

邻阶包装矩阵应具有如下与邻阶包装矩阵相似的性质：（1）由于任何原始产品，只能被至多依次封入某一个更高阶的包装中，因此对于任何一个特定的原始产品，其封装过程构成了一条链路，即非邻阶包装矩阵中，每一行至多有一个1。

对应复杂网络理论中对于路径的描述计算方法，可以运用矩阵乘法的方式来运用邻阶包装矩阵计算非邻阶包装矩阵。设两阶包装为非邻阶包装，且两阶包装相差k阶包装 （k≥2,k∈Z ）。设此k阶包装间两两的邻阶包装矩阵为A1,A2,…,Ak，则此两阶包装的非邻阶包装矩阵B可以表示为：B=A1,A2,…,Ak。

通过代数分析，可以很清晰地说明所有的非临阶包装都可以通过上面的公式计算。记第i个邻阶矩阵Ai为mi×ni阶矩阵。由于任意两个相邻的邻阶矩阵Ai与Ai+1，前一个邻阶包装中的高阶包装，为下一级邻阶包装中的低阶包装，即ni=mi+1，故矩阵乘法可以进行。进一步可以运用数学归纳法证明：B=A1,A2,…,Ak；当k=2时，若某一阶数较低的包装p封入了某一阶数较高的包装q，则Bpq=1；同时，若某一阶数较低的包装p封入了某一阶数较高的包装q，则一定有某一中间阶数的包装r，使得阶数较低的包装p直接封入了包装r，且包装r直接封入了包装q，即由矩阵运算规则而知，A1·A2矩阵的第p行第q个元素应为邻阶包装矩阵中每一行至多有一个1，同时故对于任意的因此=1=Bpq。

若某一阶数较低的包装p并未封入某一阶数较高的包装q，则Bpq=0；同时，若某一阶数较低的包装p并未封入某一阶数较高的包装q，则低阶包装p直接封入的高阶包装r，一定没有作为低阶包装封入高阶包装q，即。同样，邻阶包装矩阵中每一行至多有一个1，同时故对于任意的此时有

综上，k=2时模型公式成立。假设当k=N时成立，即：B=A1,A2,…,AN。

则当k=N+1时，设该非邻阶包装矩阵为~B。若某一阶数较低的包装p封入了某一阶数较高的包装q，则~Bpq=1；同时，若某一阶数较低的包装p封入了某一阶数较高的包装q，则一定有某一N阶包装r，使得阶数较低的包装p间接封入了包装r，且包装r直接封入了包装q，即非邻阶包装矩阵中每一行同样至多有一个1，同时Bpr=1，故对于任意的j≠r，Bpr=0。因此

因此，对于任意的k≥2,k∈Z，有B=A1,A2,…,Ak。

3 低阶包装重组对应的矩阵操作

追溯信息重新组合赋码的矩阵模型在实际应用中可以从理论角度解决重新包装的问题。对于邻阶包装矩阵，若某一低阶包装的包装p，由被封入某一高阶包装的包装q改为封入另一与包装q同阶的包装r，则只需令Apq=0，Apr=1即可。

对于非邻阶包装矩阵，任何非邻阶包装都可以拆分为邻阶包装的组合。故任何一阶包装的重组，只需要修改该阶包装的邻阶包装矩阵即可。所以，对于所有可能发生的低阶包装重组情况，都可以通过模型公式计算出所要重新改编的赋码原则并设计相应的操作流程。

包装重组对应的矩阵操作：设两阶包装为非邻阶包装，且两阶包装相差k阶包装 （k≥2,k∈Z ）。设此k阶包装间两两的邻阶包装矩阵为A1,A2,…,Ar,…,Ak，其中对于第r阶包装进行了重组，重组后的r阶邻阶包装矩阵变为，则此两阶包装的非邻阶包装矩阵可以表示为：=A1,A2,…,…,Ak。

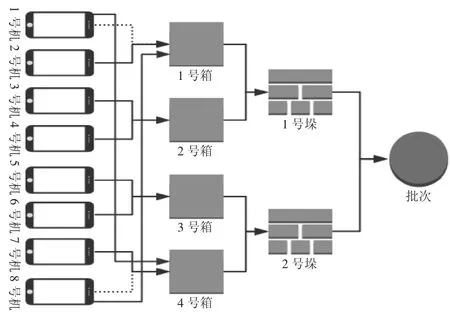
图3 包装分层示意图

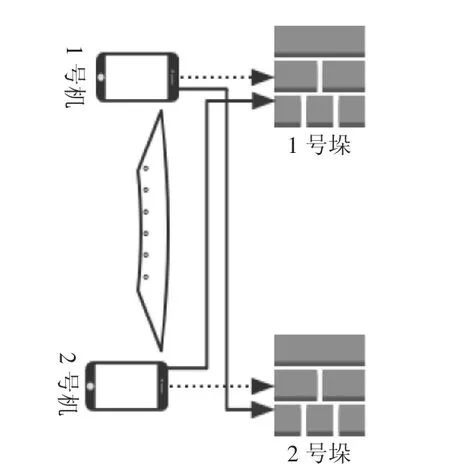
图4 非邻接包装变换示意图

如图3和图4所示，当产品更换非邻接包装时，图中的1号机和8号机原本分别隶属于1号垛和2号垛，现交换两机的摆放，使其非邻接包装发生变化；如图4所示，1号机装入2号垛，8号机装入1号垛。这种非邻接包装的变换可以等价于图3所示，1号机换入2号垛等价于1号机换入4号箱，而4号箱隶属于2号垛，因此非邻接包装的操作等价相应邻接包装的操作，即只需要对邻接矩阵作出相应的基础矩阵变换即可。因此所有的重组操作可以等价于邻接矩阵的变换。

4 总结

本文针对酒类产品在生产线追溯信息采集流程中需要对重新包装的产品进行组合赋码的问题，提出了追溯信息重新组合赋码的矩阵模型。该模型能够将不同层级的包装分阶组合实现追溯信息编码自动生成，对生产企业实现自动赋码提高流水线效率具有很强的实际意义和应用价值。

[1]何晓艳.我国农产品质量追溯体系研究[D].北京：中国农业科学院（硕士学位论文），2013.

[2]陈佳伟，刘文君.基于物联网技术的农产品供应链追溯体系研究[J].物流科技，2015,38(10):119-122.

[3]武尔维，郜鲁涛，杨林楠,等.基于Android智能终端的农产品安全追溯系统架构设计[J].云南大学学报（自然科学版），2011,33(S2):273-278.

[4]廖祎玮，郭乃文，孟圆圆,等.基于物联网的食品安全信息追溯系统[J].哈尔滨师范大学学报，2017,33(3):25-29.

[5]郑火国，刘世洪，胡海燕.食品安全追溯链构建研究[J].中国农业科技导报，2016(1):81-82.

Research on Matrix Model for Combination Traceability Information Coding

YANG Xiaohui,GUO Binghui,YIN Ziqiao,YANG Xiaobo

(School of Mathematics and Systems Science and LMIB,Beihang University,Beijing 100191,China)

With the continuous upgrading of China's economic model and consumption structure,the whole society pays more and more attention to the food safety and traceability system.In this paper,we focus on the repackaging encoding problem of product traceability information for liquor products information traceability system in the production and circulation.In the foundation of constructing liquor product traceability coding system,we propose the order packing matrix and non combination temporary ordermatrix modelforcombination traceability information coding.Furthermore,we give the combination traceability information coding process corresponding to low order repackaging combination.

traceability information;combination coding;matrix model

F253.9

A

1002-3100(2017)12-0009-04

2017-10-13

国家自然科学基金项目，项目编号：11401017、11671025、11290141。

阳晓慧（1992-），女，湖北孝感人，北京航空航天大学数学与系统科学学院、数学信息与行为教育部重点实验室硕士研究生，研究方向：复杂网络与数据分析；郭炳晖（1982-），本文通讯作者，男，内蒙古包头人，北京航空航天大学数学与系统科学学院、数学信息与行为教育部重点实验室，讲师，博士，研究方向：复杂系统、信息追溯系统；殷子樵（1996-），男，北京人，北京航空航天大学数学与系统科学学院、数学信息与行为教育部重点实验室博士研究生，研究方向：复杂网络与数据分析；杨小博（1994-），男，山东临沂人，北京航空航天大学数学与系统科学学院、数学信息与行为教育部重点实验室博士研究生，研究方向：复杂网络与数据分析。