工程供应链环境下带有价格折扣的两种材料库存模型构建与求解

张 海，杨耀红，王 帅，田 宇

（华北水利水电大学 水利学院，河南 郑州 450000）

工程供应链环境下带有价格折扣的两种材料库存模型构建与求解

张 海，杨耀红，王 帅，田 宇

（华北水利水电大学 水利学院，河南 郑州 450000）

以工程供应链中库存成本最小化为优化目标，考虑含有两种材料的价格折扣模型，构建了库存优化模型。通过Matlab中的遗传算法工具箱求解该模型，实现了库存控制的最优化问题。最后，通过一个数值算例证明了该模型的算法选用的合理性和可行性。

供应链；两种材料；价格折扣；库存优化；遗传算法

0 引 言

在工程供应链中，工程总成本超过50%～60%来源于物资和设备[1]，也就是说，在供应链管理中涉及的各种活动中，采购是最具战略性的，因为它提供了降低成本并因此增加利润的机会。工程项目由于规模巨大，物料种类繁多，在采购材料时，供应商往往会提供一些价格折扣，来刺激材料的销售，增加自身利润。折扣一般分为两种：第一，增量折扣计划，指的是一个特定折扣水平的单位价格只适用于与该水平相对应的数额的情况。第二，全量折扣计划，按折扣单价收取所有购买金额。

在近几年的研究中，Amy H.l.Lee[2]等人构造了一个混合整数规划（MIP）模型，以解决多供应商、多周期和数量折扣的批量问题。为了解决这个问题，提出了一种高效的遗传算法，目标是最小化总成本，其中成本包括订货成本、持有成本、采购成本和运输成本。Mohammad[3]等人考虑了多个供应商和数量折扣的单项动态批量大小问题，开发了一种基于Fordyce-Webster算法的新启发式算法，使解决方案得到了更高的准确性。Hesham K.Alfares[4]等人同时考虑需求率，单位持有成本和单位采购成本的变动性。根据所有单位数量折扣，存货库存模型以及销售价格独立的需求率，存储时间相关的持有成本和订单大小相关的采购成本呈现，构建了一个数学模型，并且开发了一种解决方案来确定最优解。Jonathan E.Jackson[5]等人第一次在存在数量折扣的情况下将能力视为决策变量，用拉格朗日技术和容量成本的分段线性近似，产生精确的解决方案，该算法允许在同一公共资源约束下同时混合两种最常见的数量折扣形式。Mehdi Ghaniabadi[6]等人在存在增量和全部数量折扣的情况下，讨论了供应商选择和积压的单一产品动态批量问题，提出混合整数线性规划（MILP）模型。此外，开发递归公式及其有效实现，为其提供了增量折扣案例最佳解决方案，以及针对所有单位折扣案件的近似最优解决方案。对于每种情况，使用商业软件解决MILP模型，并运行从递归公式获得的动态规划模型（FDP）及其有效实现。

人们在以往的研究中，往往是考虑单一材料的库存优化，对两种材料及多种材料的价格折扣和库存研究较少。本文主要从施工承包商的角度考虑，基于两种材料的价格折扣模型，考虑订货成本、库存持有成本和购置成本，以此来构建库存优化模型，以实现库存总成本最小。

1 基本假设与模型建立

1.1 模型假设

（1）本模型只考虑施工承包商，并涉及工程项目中所需材料的两种产品，且这两种产品相互独立，没有关联性。

（2）假定工程项目不允许缺货，不存在缺货成本，且每次订货不能超过最大库存容量。

（3）材料供应商自行生产产品，且其单位产品的成本不变。

（4）模型采取连续库存检查补货策略，即Q,（）R 策略。一旦库存水平低于再订货点，马上发出订货量为Q订单。

（5）假定供应商提供的产品价格是出厂价（不包含运输费用），由供应商承担运输成本。

（6）订货提前期为零。

1.2 模型符号

为了描述本文的数学模型和方法，考虑以下符号：

Q为库存的最大容纳量；ψm为订购m材料的每次订货成本；ψn为订购n材料的每次订货成本；Qm为材料m每次的订货批量；Qn为材料n每次的订货批量；M为材料m的订货次数；N为材料n的订货次数；αm为材料m的价格折扣率；αn为材料n的价格折扣率；Pm为材料m无价格折扣时供应商给承包商的单位产品价格；Pn为材料n无价格折扣时供应商给承包商的单位产品价格；hm为材料m的单位持有成本；hn为材料n的单位持有成本；Sm为材料m的安全库存，即低于该库存立即订货；Sn为材料n的安全库存，即低于该库存立即订货。

其中：下标m和n分别指工程上的两种材料，订货批量Qm、Qn，订货次数M、N为决策变量。

1.3 工程供应链中库存模型成本分析

在供应链中，每一个供应商为了获得一个更大的购买量而降低产品的价格，这样既能实现自己产品的销售、增加利润，还能给施工承包方带来便利。在实际情况中，供应商会针对不同的订货量提供不同的优惠价格。假设在模型中，两种材料的价格折扣率分别是αm和αn，αm和αn都是分段函数。m材料的数量折扣函数为：

其中：Qmi＜Qm（i+1）,0.5＜αm＜1, αm1＞αm2＞…αmi＞αmγ。

n材料的数量折扣函数为：

其中，Qni＜Qn（i+1）,0.5＜αn＜1, αn1＞αn2＞…αni＞αnγ。

1.3.1 订货成本

施工承包商在一个周期内的订货成本与订货数量无关，只与订货批次有关，其订货成本等于每次订货成本与订货次数之积：

1.3.2 购置成本

施工承包商的购置成本是指在购买所需材料时需要付出的成本，由订货数量和单位产品的购买价格决定，等于订货数量与材料的单位购买价格之积。在工程项目的实际情况中，供应商往往会根据承包商的订货策略进行价格上的优惠，在模型中，供应商提供关于订货量的价格折扣，其购置成本为：

1.3.3 库存持有成本

施工承包商的库存持有成本是指在库存中持有这两种材料所产生的存贮费用，其中包括仓库的保管费、材料的保护措施费、材料占用资金的利息等。施工承包商采取连续性检查库存策略，当库存量降到库存订货点时开始订货，每次订货量为Qm和Qn两种材料的和，施工承包商的库存持有成本等于材料的单位持有成本与平均库存量之积：

1.4 工程供应链的库存成本

由式（3）、式（4）、式（5） 可以确定工程供应链的库存成本为：

模型的决策变量为Qm、Qn、M、N。

目标函数为：

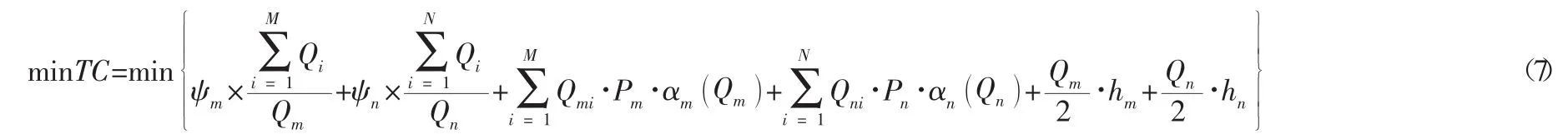
约束条件为：

其中约束条件：式（8）表示两种材料的订货批量不允许超过最大仓库容纳能力。式（9） 和式（10）表示两种材料的订货量大于0。

2 模型求解

与传统算法相比较，遗传算法搜索能力比较强，而且具有极强的鲁棒性。考虑到遗传算法在优化方面具有强大的功能，且实数编码的遗传算法对于求解非线性库存优化问题效果较好，因此选择遗传算法对库存优化模型进行求解可以取得较理想的结果。

在Matlab中，调用遗传算法工具箱中的函数对目标函数进行编程求解，得出库存最小成本。

3 案例与分析

某建设项目合同工期为40个月，施工承包商向材料供应商订购m和n两种材料，并且，材料供应商根据订购批量提供数量折扣，如下所示：

其中：Qm和Qn单位为吨。

工程项目实例中其他参数如表1所示。

表1 算例相关参数表

其中：库存最大容纳量为MaxQ=640吨。

在本案例中，种群规模设为200，变异概率为0.35，交叉概率为0.5。遗传算法一般用于求解函数的近似最优解，而不是最优解，并且遗传算法的收敛性取决于其最初值，所以需要多次运行Matlab程序。多次运行主程序得到图1。

从遗传算法优化成本迭代曲线可以看出遗传迭代数达到10次左右，最优解和种群平均值开始趋于稳定。

两种材料的库存状况变化如图2所示。

两种材料的库存状况在设定周期内呈波动性变化，符合工程实际。

通过Matlab求解可以求得最优解如下：

根据优化算法的结果，我们可以确定库存成本的最小值为659 488元，供应链的最优订货策略为：施工承包商订购m材料的订货次数为2，订购n材料的订货次数为4，m材料的最优订货批量为49吨，n材料的最优订货批量为318吨。通过比较，可以发现两种材料放在一个库里考虑，比分别放在两个库里成本优化了很多，结果也更合理化。

图1 遗传算法优化成本迭代曲线

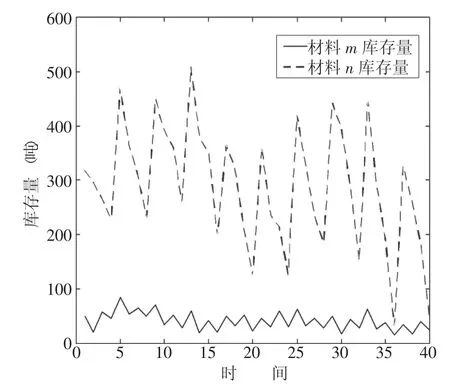
图2 货物m和n的库存状况变化

4 结束语

本文从施工承包商的角度考虑，对工程供应链中订购两种材料进行建模和分析，最后选取一个工程案例进行优化计算，得到了该工程项目供应链的最小库存成本以及最优订货策略，验证了构建的优化模型的可行性和适用性。在本文中，该模型只是针对两种相互独立的材料来考虑的，接下来可以讨论两种材料在相关性情况下库存的变化。

[1]李民，高俊.工程供应链管理研究综述[J].工业技术经济，2012(5):28-37.

[2]Lee A H I,Kang H Y,Lai C M,et al.An integrated model for lot sizing with supplier selection and quantity discounts[J].Applied Mathematical Modelling,2013,37(7):4733-4746.

[3]Mazdeh M M,Emadikhiav M,Parsa I.A heuristic to solve the dynamic lot sizing problem with supplier selection and quantity discounts[J].Computers&Industrial Engineering,2015,85:33-43.

[4]Alfares H K,Ghaithan A M.Inventory and pricing model with price-dependent demand,time-varying holding cost,and quantity discounts[J].Computers&Industrial Engineering,2016,94:170-177.

[5]Jackson J E,Munson C L.Shared resource capacity expansion decisions for multiple products with quantity discounts[J].European Journal of Operational Research,2016,253(3):602-613.

[6]Ghaniabadi M,Mazinani A.Dynamic lot sizing with multiple suppliers,backlogging and quantity discounts[J].Computers&Industrial Engineering,2017,110:67-74.

Construction and Solution of Two Kinds of Material Inventory Models with Price Discount in Engineering Supply Chain Environment

ZHANG Hai,YANG Yaohong,WANG Shuai,TIAN Yu

(School of Water Conservancy,North China University of Water Resources and Electric Power,Zhengzhou 450000,China)

In this paper,we minimize the inventory cost in the engineering supply chain as the optimization target,consider the price discount model with two kinds of materials,and build the inventory optimization model.We solved the model through the genetic algorithm toolbox in matlab,and realized the optimization problem of inventory control.Finally,we prove the rationality and feasibility of the algorithm selection by a numerical example.

supply chain;two kinds of materials;price discount;inventory optimization;Genetic algorithm

F253

A

1002-3100(2017)12-0021-04

2017-10-16

张 海（1992-），男，河北邢台人，华北水利水电大学水利学院水利工程专业硕士研究生，研究方向：供应链管理；杨耀红（1969-），男，河南漯河人，华北水利水电大学水利学院，教授，博士，研究方向：工程管理、供应链管理。