一类由Hurwitz-Lerch Zeta函数定义的亚纯函数的系数估计

石磊

(安阳师范学院 数学与统计学院,河南 安阳 455002)

一类由Hurwitz-Lerch Zeta函数定义的亚纯函数的系数估计

石磊

(安阳师范学院 数学与统计学院,河南 安阳 455002)

利用Hurwitz-Lerch zeta函数定义了一类新的算子,运用该算子和卷积定义了一类新的亚纯函数。讨论了该函数类的包含关系、系数估计和充分条件等性质,所得结果推广了一些已有的结论。

亚纯函数;Hurwitz-Lerch zeta函数;卷积;系数估计

0 引言

设M表示在单位去心圆盘U*={z:0<|z|<1}=U{0}内解析且形如

(1)

的函数全体。

设函数f,g∈M, 其中f由(1)给出,

f与g卷积f*g定义为

则称f∈MS*(θ,γ)为γ阶亚纯螺旋函数。有关亚纯螺旋函数的相关研究,可参考[1-3]。

若f∈M满足

则称函数f∈MD*。此类函数由Kumar和Shukla[4]引入研究。

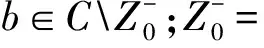
定义1 如果函数f∈M满足条件

当对函数类MSDs,b(λ,α,β)的参数取一些特殊值时,可以得到亚纯函数的一些特殊子类[7-10]。 本文我们将讨论函数类MSDs,b(λ,α,β)的系数估计问题, 所得结果推广了一些已有的结论。

1 主要结果

定理1 设0≤α≤β,f∈MSDs,b(λ,α,β). 则有f∈MSDs,b(λ,0,ζ), 这里

证明设f∈MSDs,b(λ,α,β)。 由定义可知

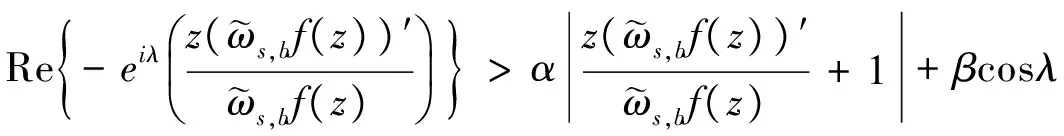
注意到

我们有

从而,

这里

由假设0≤α≤β,0≤β<1, 易见0≤ζ<1, 故f∈MSDs,b(λ,0,ζ).

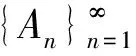
(2)

则

(n≥2).

证明由(2)式, 可得

(3)

和

(4)

结合(3)和(4), 则

(n∈N).

从而对n≥2,我们有

这就完成了引理1的证明。

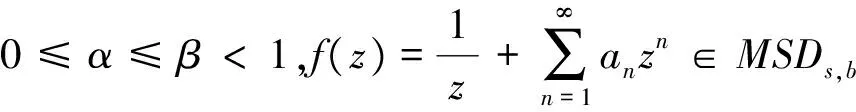
证明假定f∈MSDs,b(λ,α,β)。 由定理1,我们知道

(5)

对(5)式变形可得

即

比较两边zn的次数, 则有

因为|τk|≤2(k∈N), 故

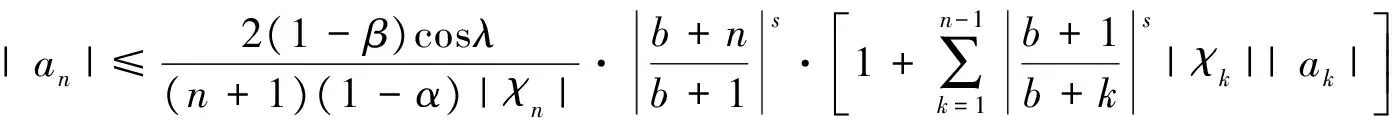
(6)

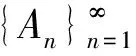
(7)

为了证明

|ak|≤Ak(k∈N),

我们采用数学归纳法。 首先

因此,我们假定|ak|≤Ak(k=1,2,…,n)。 由(6)和(7)可得

由数学归纳法可知|ak|≤Ak(k∈N). 结合引理1即得定理2的系数估计。

定理3 若f∈M满足

(8)

则f∈MSDs,b(λ,α,β).

证明由(8)我们有

故

设

由最大模原理, 我们有

注意到

我们有

α|η(z)+1|-Re{-eiλη(z)}+βcosλ=

α|η(z)+1|-Re{-eiλη(z)-eiλ}-(1-β)cosλ≤

(1+α)|η(z)+1|-(1-β)cosλ<0.

从而f∈MSDs,b(λ,α,β),这就完成了定理3的证明。

[1] Al-Amiri H,Mocanu P T.Some Simple Criteria of Starlikeness and Convexity for Meromorphic Functions[J].Mathematica(Cluj),1995,37(60):11-21.

[2] Liu J L,Srivastava H M.A Linear Operator and Associated Families of Meromorphically Multivalent Functions[J].JournalofMathematicalAnalysisandApplications,2001,259(2):566-581.

[3] Xu N,Yang D.On Starlikeness and Close to Convexity of Certain Meromorphic Function[J].JKoreanSocMathEdusSerB:ThePureandAppliedMathematics,2003,10(1):566-581.

[4] Kumar V,Shukla S L.Certain Integrals for Classes of p-valent Meromorphic Functions[J].BulletinoftheAustralianMathematicalSociety,1982,25(1):85-97.

[5] Srivastava H M,Attiya A A.An Integral Operator Associated with the Hurwitz-Lerch Zeta Function and Differential Subordination[J].IntegralTransformsandSpecialFunctions,2007,18(34-4):207-216,DOI:10.1080/106524607012085-77.

[6] Ghanim F.A Study of a Certain Subclass of Hurwitz-Lerch-Zeta Function Related to A Linear Operator[J].AbstractandAppliedAnalysis,2013,2013(1):1-7.

[7] Sun Y,Jiang Y P,Liu Z H.Some Subclasses of Meromorphic Multivalent Functions Involving a Generalized Differential Operator[J].HacettepeJournalofMathematicsandStatistics,2014,43(3):435-449.

[8] Sun Y,Jiang Y P,Rasila A,etal.Integral Representations and Coefficient Estimates for A Subclass of Meromorphic Starlike Functions[J].ComplexAnalysisandOperatorTheory,2016:1-19.DOI:10.1007/s11785-016-0531-x.

[9] Wang Z G,Srivastava H M,Yuan S M.Some Basic Properties of Certain Subclasses of Meromorphically Starlike Functions[J].JournalofInequalitiesandApplications,2014,2014(1):1-13,DOI:10.1186/1029-242X-2014-29.

[10] Nunokawa M,Sokol J.On Meromorphic and Starlike Functions[J].ComplexVariablesandEllipticEquations,2015,60(10):1411-1423,DOI:10.1080/17476933.2015.1022170.

CoefficientEstimatesonCertainSubclassofMeromorphicFunctionsDefinedbyHurwitz-LerchZetaFunction

SHI Lei

(SchoolofMathematicalScienceandStatistics,AnyangNormalUniversity,Anyang455002,China)

We introduce and investigate a certain subclass of meromorphic functions by using of an operator defined by the Hurwitz-Lerch Zeta function. Such results as inclusion relationships, coefficient estimates and sufficient conditions are proved. The results presented here would provide extensions of those given in earlier works.

meromorphic function;Hurwitz-Lerch zeta function;hadamard product;coefficient estimates

10.13451/j.cnki.shanxi.univ(nat.sci.).2017.04.008

2016-07-22；

2016-12-17

国家自然科学基金(11301008； 11426035)；河南省高等学校重点科研项目(17A110014)

石磊(1982-),男,河南信阳人,讲师,研究方向:几何函数论。E-mail:shimath@126.com

O174.51

A

0253-2395(2017)04-0712-05