一种基于混合度的层次粒度SVM算法

程凤伟,郭虎升

(1.太原学院 计算机工程系,山西 太原 030032;2.山西大学 计算机与信息技术学院，山西 太原 030006)

一种基于混合度的层次粒度SVM算法

程凤伟1,郭虎升2*

(1.太原学院 计算机工程系,山西 太原 030032;2.山西大学 计算机与信息技术学院，山西 太原 030006)

随着现实生活中数据集规模的不断增大,设计有效的分类算法势在必行。支持向量机(Support vector machine,SVM)是一种公认的性能较好的分类算法，目前一些SVM算法是针对减少支持向量的数目来提高分类的效率。文章提出一种基于混合度的层次粒度支持向量机算法(Hierarchical Granular Support Vector Machine Algorithm based on Mixed,MHG-SVM),利用混合度对已有的层次粒度SVM分类算法进行了改进,该算法通过定义一个数据置信度和一个粒度参数挑选出重要的分类信息。从实验结果可以看出,提出的算法在处理大规模数据集方面,保持了较高的分类精度,而且支持向量机的学习和分类速度也取得了大幅度提高。

支持向量; 分类精度;混合度;置信度;大规模数据集

0 引言

支持向量机是一种通用有效的学习方法,在处理小规模二分类问题时表现出较好的性能,但在处理大规模数据集时,效率低下[1-2]。2004年Tang提出了一种新的机器学习模型[3-4]——粒度支持向量机(Granular Support Vector Machine, GSVM),它以粒度计算理论[5-7]和统计学习理论为基础,有效地克服了传统支持向量机在处理大规模数据集时训练效率低下的问题,而且也可保持较高的泛化性能[8-9]。典型的GSVM 模型主要有:基于关联规则的GSVM[10]、基于聚类的GSVM[11-12],此外,也有不少的学者研究基于粗糙集[13]、决策树[14]、商空间[15]以及神经网络[16]的GSVM 学习方法。

本文提出的基于混合度的层次粒度SVM算法不同于传统层次粒度SVM算法,第一,MHG-SVM算法不建立两棵层次树,只构建一个;第二,MHG-SVM算法从树的顶层开始反复训练支持向量节点,因为越是树的顶层,树的节点覆盖越大的样本空间,很有可能发现节点是混合节点。对于混合节点,用k-means聚类算法,对它们进行继续粒划,保留纯节点,删除无效节点,采用此层次粒划模型对样本集进行筛选,提取重要的分类信息加入到训练集进行训练,获得了较好的泛化能力。

1 基于混合度的层次粒度SVM模型

传统层次粒度SVM 模型建立两棵层次树,分别对正类样本和负类样本进行操作,一棵树上的节点只包含一类分类信息,而采用这种传统层次粒度GVM模型大多在原空间构建层次结构,而在核空间进行SVM训练,会存在操作前后模型误差问题,而且它的粒划分过程是静态的,每层粒划参数需要由用户给出,而不能根据自身问题实现动态控制。本文提出的MHG-SVM算法,采用动态层次粒划机制,首先把整个数据集作为树的根节点,进行混合粒划分,粒划后的子粒作为子节点,并计算子节点(子粒)的密度与混合度,根据密度和混合度将子节点分为三部分:混合节点、纯节点、无效节点。对于混合节点,由于其含有大量的分类信息,需要细化,将其作为父节点进行下一层次的粒划分,划分出的粒作为子节点,重复此过程,直到达到一定的纯度,不再分裂节点。对于纯节点,由于只包含正类(或负类)的样本,含有较少的分类信息,因此将其作为叶子节点,不再对其进行粒划分。对于无效节点,由于其含有较少的样本,直接删除。最后,提取树中所有叶子节点上粒的代表点加入到训练集,进行SVM训练。这种基于混合度的层次粒度SVM算法,通过度量节点上粒的混合度,压缩纯粒,缩减了训练集,通过度量粒的混合度和粒密度,细化信息粒,从而选取更多的支持向量扩充到训练集,使得训练集样本的分布更符合原始数据集样本的分布,这样训练得出的超平面更加准确。图1给出了基于混合度的层次粒度SVM粒划分的示意图。 假设经过对整个数据集初次粒划分,得到A、B、C、D、E、F六个粒,从图中可以看出,A,B为混合粒,需要进行再次粒划分,挑选更多的分类信息加入到训练集;C、D为含有少量异类样本的粒,由于其混合度较低常被看作纯粒处理,只需取C、D粒中代表点(粒中心)加入训练集即可;E、F是由分布离群的噪声样本在粒划过程中单独构成一个粒,称为无效粒,这种粒往往由于密度太低而被安全删除,这样就会减少噪声对分布问题的影响。

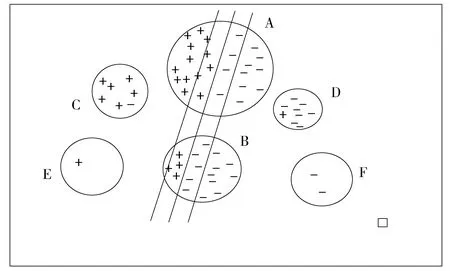
Fig.1 Process of granular division图1 粒划分示意图

MHG-SVM模型在建树过程中需要区分三种节点:混合节点、纯节点和无效节点。在本文中,无效节点由粒的支持度(粒密度)进行筛选,混合节点和纯节点由混合度进行筛选区分。

用Mix(Hk)表示粒Hk的混合度,它反应粒中正负样本的混合程度,从式(1)可以看出,Mix(Hk)∈[0,1],Mix(Hk)值越大,表示粒Hk的混合度越高,含有的分类信息越多;Mix(Hk)值越小,表示粒Hk的混合度越低,粒越纯,含有的分类信息越少;当Mix(Hk)=0时表示粒Hk是纯粒。其定义如下:

(1)

粒中心反映一个粒的位置,它作为粒中代表点参与训练,其定义如下:

(2)

粒的支持度(粒密度)反映一个粒的重要程度,决定一个粒是参与训练还是被删除。其定义如下:

(3)

MHG⁃SVM学习算法输入：训练集T={X，Y}={(xi，yi)}li=1，测试集T′={(xj，yj)}l′j=1，支持度界值 D，混合度界值Mix，粒划参数k，核函数K，正则参数C。Step1：对训练集进行粒划，得到一系列粒H={Hk}lk=1，其中Hk为粒划分后得到的一个粒。Step2：设置混合度界值Mix和支持度界值 D。Step3：由公式(1)(2)(3)计算每个粒的混合度Mix(Hk)和支持度DHk，根据混合度界值Mix和支持度界值 D将由Step1得到的一系列粒{Hk}lk=1分为混合粒、纯粒和无效粒。Step4：从粒集H中删除无效粒，对于混合粒，根据粒划参数k进行再次粒划，用粒划后得到的粒代替原来的粒放到粒集H中，然后转入Step2，直到所有粒都不满足粒划条件，即粒集H中所有粒都是纯粒。Step5：取粒集H中的所有粒(纯粒)的中心作为训练数据进行训练，得到分类超平面。Step6：返回分类超平面f(x)=sgn(W∗φ(x)+b)。

就传统的SVM而言,由于所有的样本都要加入训练集进行训练,因此,训练的空间复杂度和时间复杂度都非常高,而本文采用的MHG-SVM算法采用层次粒划分模型,细化重要的分类信息,删除噪声粒,很大程度上缩减了训练集的规模,提高了分类的速度。

2 实验结果

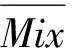
对于传统的GSVM算法而言,最终粒划分的个数由初始粒划参数决定,而MHG-SVM算法根据每个粒的混合度和支持度对数据集进行动态粒划分,因此,预测初始粒划参数对MHG-SVM算法分类正确率的影响相对较小。为了进一步验证初始粒划参数K对MHG-SVM算法影响,在标准数据集上进行了实验分析。图2给出了MHG-SVM与GSVM算法测试结果的比较。

从实验结果可以看出,对于GSVM算法,影响算法表现的主要因素是初始粒划参数的设定,随着粒划参数K的增加,算法的正确率逐渐升高,对于MHG-SVM算法,在所有的数据集上,正确率都高于GSVM,且正确率并没有随着初始粒划参数K的增加呈现明显变化趋势,正确率很平稳,几乎不受初始粒划参数的影响。

表1 实验采用的数据集Table 1 Datasets used in the experiment

Fig.2 Result comparison between MHG-SVM and GSVM图2 MHG-SVM与GSVM算法测试结果的比较

为了进一步研究MHG-SVM的性能,本文在几个数据集上衡量了初始粒划参数取值不同的情况下最终参加SVM训练的粒的个数。图3给出了粒划程度的详细信息。

Fig.3 Final number of granularity for MHG-SVM algorithm图3 采用MHG-SVM算法最终获得粒的个数

从图3容易看出,对于German、Image、Diabetis、Heart、Breast-cancer数据集,采用MHG-SVM算法后,尽管初始粒划参数的值不同,但最终得到支持向量的数目基本一致;对于Throid数据集,支持向量数目受初始粒划参数影响,原因在于Throid数据集本身比较小,粒划后得到的粒的个数少,所以才会接近初始粒划参数。因此,MHG-SVM算法采用混合度层次粒划分机制使得训练结果比较稳定,具有较好的鲁棒性。

表2是MHG-SVM、DGSVM、GSVM和传统SVM测试结果的比较,初始粒划参数分别取10,50和200。从表中可以看出,与传统SVM算法相比,另外三个基于GSVM算法的训练效率都提高100倍以上,尽管SVM的泛化性能在所有方法中最好,但其训练时间太长,无法进行高效学习。MHG-SVM算法与GSVM算法相比,运算速率虽有所下降,但运算正确率有一定提升。MHG-SVM算法与DSVM算法相比,从整体上看,MHG-SVM算法的运算效率和正确率都有所提高。

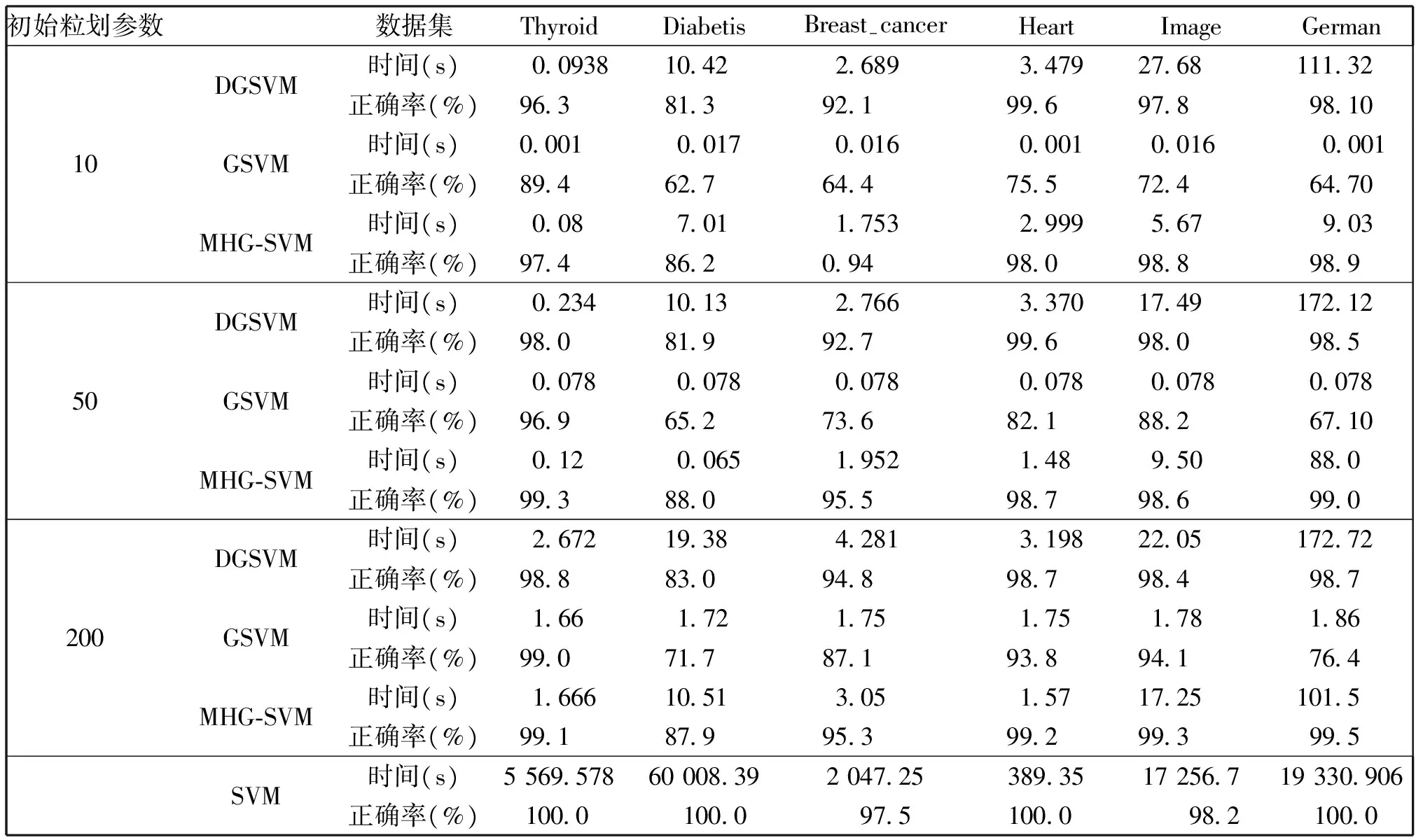
表2 四种方法测试结果的比较Table 2 Comparison of four kinds of test results

上述实验结果表明,基于MHG-SVM算法能有效提取支持向量信息,减小模型误差,可以获得较好的泛化性能,而且采用粒支持度进行过滤,剔除一些不重要的粒,保证样本处理与训练分布的一致性；另一方面,采用混合度,提取含有重要信息的混合粒;然后再通过采用动态粒划分机制,对初始超平面进行更新,更进一步地提高了MHG-SVM的泛化性能。

3 结束语

本文提出了一个新的处理大规模数据集的混合度MHG-SVM算法,由于传统的GSVM算法在处理大数据集的分类问题时泛化能力有限,MHG-SVM算法通过设置混合度和支持度界值,可以有效地挑选出重要的分类信息,从而克服了GSVM算法在处理分类问题时运算精度低下的问题。未来的工作中,考虑将MHG-SVM算法扩展到多分类分布不均匀的数据分类问题的处理当中,此外,可将本文的算法应用到网页分类疾病监测等大规模分布不均匀的实际问题当中。

[1] James M,Mihael C,Brad B,etal.Big Data:The Next Frontier for Innovation,Competition,and Productivity[R].Mckinsey & Company,2011,05.[http:∥www.mckinsey.com/insights/business-technology/big-data-the-next-frontier-for-innovation].DOI:https:∥doi.org/10.1586/17512433.2014.905201.

[2] Tang yukun,Jin bo,Zhang yanqing.Granular Support Vector Machines for Medical Binary Classification Problems[J].ComputationalIntelligenceinBioinformaticsandComputationalBiology,2004:73-78.

[3] Wang wenjian,Guo husheng,Jia yuanfeng,etal.Granular Support Vector Machine based on Mixed Measure[J].Neurocomputing,2013,101(4):116-128.DOI:https:∥doi.org/10.1010/j.neucom.2012.08.006.

[4] Yao Y Y.Perspectives of Granular Computing[C]∥Proceedings of 2005 IEEE International Conference on Granular Computing,2005,1:85-90.DOI:https:∥doi.org/10.1109/wi.2007.159.

[5] Xu C F,Wang J L.An Efficient Incremental Algorithm for Frequent Itemsets Mining in Distorted Databases with Granular Computing[C]∥International Conference on Web Intelligence,2006,37:913-918.

[6] Yao Y Y.Granular Computing for Web Intelligence and Brain Informatics[C]∥International Conference on Web Intelligence,2007,62:1-4.

[7] Guo husheng,Wang wenjian,Men changqian.A Novel Learning Model-kernel Granular Support Vector Machine[C]∥Proceedings of 2009 International Conference on Machine Learning and Cybernetics.Baoding, China,IEEE Press,2009：930-935.DOI:https:∥doi.org/10.1109/icmlc.2009.5212413.

[8] Tang yuchun,Jin bo,Zhang yanqing.Granular Support Vector Machines with Association Rules Mining for Protein Homology Prediction[J].ArtificialIntelligenceinMedicine,2005,35(1):121-134.

[9] Tang Y C,Jin B,Zhang Y Q.Granular Support Vector Machines with Association Rules Mining for Protein Homology Prediction[J].ArtificialIntelligenceinMedicine,2005,35(1):121-134.

[10] Yu H,Yang J,Han J W.Classifying Large Data Sets using SVMs with Hierarchical Clusters[J].KnowledgeDiscoveryandDataMining,2003,9:306-315.

[11] Wang W J,Xu Z B.A Heuristic Training in Support Vector Regression[J].Neurocomputing,2004,61:259-275.

[12] Chen R C,Cheng K F,Hsieh C F.Using Rough Set and Support Vector Machine for Network Intrusion Detection System[J].InternationalJournalofNetworkSecurity&ItsApplications,2009,59:465-470.DOI:https:∥doi.org/10.1109/aciids.2009.59

[13] Arun Kumar M,Gopal V.A Hybrid SVM based Decision Tree[J].PatternRecognition,2010,43(12):3977-3987.DOI:https:∥doi.org/10.1016/j.pat.cog.2010.06.010.

[14] Cui H X,Zhang L B,Kang R Y,etal.Research on Fault Diagnosis for Reciprocating Compressor Valve using Information Entropy and SVM Method[J].JournalofLossPreventionintheProcessIndustries,2009,22(6):864-867.DOI:https:∥doi.org/10.1016/j.jlp.2009.08.012.

[15] Anguita D.Improved Neural Network for SVM Learning[J].NeuralNetwork,2002,13(5):1243-1244.

[16] 程凤伟,王文剑,郭虎升.动态粒度SVM算法[J].模式识别与人工智能,2014(4):1799-1802.

AHierarchicalGranularSupportVectorMachineAlgorithmbasedonMixed

CHENG Fengwei1,GUO Husheng2*

(1.DepartmentofComputerEngineeringTaiyuanUniversity,Taiyuan030032,China;2.SchoolofComputerandInformationTechnology,ShanxiUniversity,Taiyuan030006,China)

The increasing size and dimensionality of real-world datasets make it necessary to design efficient classification algorithms.Support vector machine(SVM) is an acknowledged classification algorithm with good performance,and some SVM algorithms are aimed at reducing the number of support vector to improve the efficiency of classification.This paper proposes a hierarchical granularity support vector machine algorithm based on mixed,namely MHG-SVM,using the mixing degree to improve the existing hierarchical granularity support vector machine algorithm.The proposed algorithm defined a data granularity of confidence and a parameter to select important classification information, and then put them in training set to SVM training.The experimental results indicate that the improved algorithm is suitable for processing large number of observations and can effectively accelerate SVM learning while keeping the classification precision.

support vector;classification precision;mixing degree;granularity of confidence;large number of observations

10.13451/j.cnki.shanxi.univ(nat.sci.).2017.04.010

2016-12-30；

2017-02-07

山西省自然科学基金(2015021096)，山西省高等学校科技创新项目(2015110)

程凤伟(1988-),女,河南周口人, 硕士,助教，研究方向:人工智能, 机器学习。E-mail:867964783@qq.com

*通信作者：郭虎升(GUO Husheng)，E-mail:guohusheng@sxu.edu.cn

TP301

A

0253-2395(2017)04-0750-06