光栅外腔反馈半导体激光器及稳频系统的动态特性测试

秦利娟,秦林,王彦华,2*,王军民

(1.山西大学 物理电子工程学院,山西 太原 030006;2.量子光学与光量子器件国家重点实验室 山西大学 光电研究所,山西 太原 030006;3.山西大学 极端光学协同创新中心,山西 太原 030006)

光栅外腔反馈半导体激光器及稳频系统的动态特性测试

秦利娟1,秦林1,王彦华1,2*,王军民2,3

(1.山西大学 物理电子工程学院,山西 太原 030006;2.量子光学与光量子器件国家重点实验室 山西大学 光电研究所,山西 太原 030006;3.山西大学 极端光学协同创新中心,山西 太原 030006)

能够在复杂的使用环境中保持输出激光频率稳定一直都是激光器研究的重要内容。人们不仅需要直接优化系统结构,还应对系统特性进行针对性地校正和优化。文章构建了一套高效、高分辨率测量激光频率变化的实验系统,通过研究激光器被调制后的输出频率变化,可获得在实验室环境中ECDL激光器及其稳频系统的动态响应。实验中记录了正弦点频和方波两种信号调制后激光频率的响应,在进行FFT分析后获得了幅频特性和相频特性。结果表明方波调制信号测量方案同正弦点频测量方案结果一致,而且不需要多次测量,测量效率高。利用该测量系统还可以获得机械冲击后激光器的幅频特性,可用于分析闭环系统的冲击响应特征,从而为类似环境中闭环系统参数校正和优化提供实验依据。

动态响应;频率响应特性;ECDL激光器;激光器稳频

0 引言

当前常见的半导体激光器多为外腔反馈式(External-Cavity Diode Laser,ECDL)、分布反馈式(Distributed Feedback Laser,DFB)、布拉格反馈式(Distributed Bragg Reflector,DBR)或垂直腔面发射激光器(Vertical-Cavity Surface Emitting Laser,VCSEL)等,它们各有特点。通常DBR或DFB半导体激光器仅有几兆赫兹的线宽,机械稳定性好,有广泛的应用。尽管DFB结构的激活介质还可获得较高的输出功率[1],但当大功率工作时这些激光器都容易损坏,运行成本相对较高。VCSEL输出易于调制、光束发散角好且寿命长,但线宽在百兆赫兹,输出功率较小,只有毫瓦级[2]。外腔反馈半导体激光器可通过诸如FP腔、标准具、平面镜或光栅构建光反馈,又增加了一个可操控因素,具有广泛的应用。特别是光栅外腔反馈的ECDL激光器具有压窄线宽、单模输出、连续可调谐等优点,适用于很多科学研究及精密测量领域。不过用来构成反馈的光栅外腔使激光器频率对机械结构以及空气的流动都非常敏感,所以优化它的主动稳频系统和提高机械稳定性成为改进ECDL激光器特性的关键问题[3]。在1983年,PDH稳频方法的应用使得激光器特性得到极大的改善[4]。2012年德国研究人员通过改进结构设计和优化反馈环路获得了等效线宽35 mHz的激光输出[5]。但根据肖洛-汤斯极限线宽的计算方法,激光器的线宽极限在mHz量级[6]。所以对稳频系统的改进依然还有很大的提升空间。在高精度的控制和测量时,闭环反馈可增加测量带宽、提高测量分辨率,已成为精密测量和控制系统的基本需求[7-9]。特别是对于高稳定窄线宽的激光器系统,系统环路的研究非常重要[10],而包括引力波探测[11]和获得15 dB压缩真空态的最新纪录均得益于激光器控制系统动态特性及频率稳定性的系统研究[12]。

系统的动态特性可以用微分方程、传递函数、频率特性等形式从不同的角度来描述,主要表征系统随时间变化的输入量、输出量以及系统内部各个参量之间的关系,是对系统进行设计、分析和校正的基础。微分方程可准确、直观地描述系统时域中的特性,但不便于分析系统参数变化后的规律;传递函数是在拉普拉斯变换基础上定义,在复数域中描述系统的特性,可以用来研究系统结构或参数变化对系统性能的影响。以传递函数为基础的根轨迹法和频域法是广泛采用的系统分析方法。但真实系统的数学模型不可能非常准确,其频率响应特性通常靠实验的方法测定,特别是对于系统非线性特性的分析和校正过程,实验的方法更有效。频率响应特性不是简单的稳态正弦响应,其包含了幅频特性和相频特性,可全面反映系统动态过程[13]。实际上真实稳频反馈控制系统在实验室外复杂的环境中,还会有很多的干扰源,更需要通过实验获得系统的动态特性,用于调整自身参数以优化如谐振频率,带宽等系统特性来适应环境。

本文从自动控制系统的角度研究激光器的频率稳定性,重点分析了激光器稳频系统的闭环负反馈环路动态特性。我们在实验中采用自制的高稳定ECDL,激光器输出频率的调制信号(正弦点频和方波)由恒流源电流调制端口引入,并通过测频系统来获得激光频率变化,经FFT分析激光器系统输出频率的动态响应特性,获得开环和稳频闭环系统的幅频特性和相频特性。实验表明方波扰动测量系统响应的方法高效且可靠,大大简化了实验过程。通过该系统可以很好地区分出两个频率差为0.008 Hz的频率调制信号,其最高频率分辨率可达0.002 Hz。在此基础上可分析激光器系统在外界冲击下的响应,为经受冲击时稳频系统的参数选择和针对性校正提供实验参考,使得激光器将来可以应对更恶劣的环境。

1 测量激光器动态特性的实验系统

测定系统的频率响应特性就是分析系统响应同输入时变信号的关系,并绘制出直观的特性曲线。调制通常可选正弦波、锯齿波(斜升)、阶跃或脉冲信号等。实验系统如图1所示,Littrow结构(未画出)的光栅外腔反馈半导体激光器需要有控温仪、激光二极管的恒流源和利用压电陶瓷控制光栅反馈的高压放大器。实验中调制激光频率的信号通过激光器恒流源的电流调制端口引入,同时利用测频系统可得到激光器在饱和吸收峰中心频率附近的频率变化,从而获得开环或稳频闭环以后系统的调制响应,利用存储示波器实时记录并利用FFT进行数据分析就可以测量激光器输出频率受调制的动态响应。

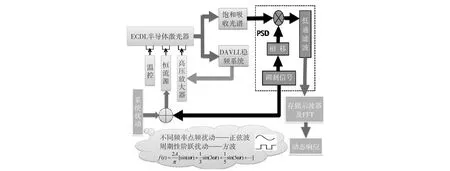
Fig.1 Experiment system set-up. Frequency stabilization system is Dichroic Atomic Vapor Laser Lock (DAVLL). Through the modulation port of the high voltage amplifier, the ECDL laser closed-loop is constructed. Based on the saturated absorption spectrum (SAS), a light frequency measurement system near the center of SAS absorption spectrum is demonstrated by phase sensitive detection (PSD). The dynamic response for sinusoidal wave or square wave introduced by the constant-current source modulation port are obtained via the storage oscilloscope and FFT analysis图1 实验系统图.实验系统由稳频和测频两部分构成。稳频系统采用磁致二色性激光锁频 (Dichroic Atomic Vapor Laser Lock, DAVLL)方案,鉴频信号经高压放大器调制端口加载到ECDL激光器反馈光栅的压电陶瓷上构成闭环反馈稳频;测频系统利用饱和吸收光谱(Saturated Absorption Spectrum, SAS)提供频率参考,经相敏检波(Phase Sensitive Detection, PSD)可获得在饱和吸收峰中心频率附近的激光频率变化。外部的正弦点频或方波调制由恒流源调制端口引入,经存储示波器和FFT分析后可获得系统的动态响应

要方便获取系统的动态响应需要具备两个重要的条件:稳定的激光器系统和在光频段频率变化赫兹量级的高精度测量。为了提高光栅反馈结构的稳定性,我们借鉴柔性铰链的结构设计了三个可独立调节的面接触转动副[14]调整其机械结构,分别使光栅反馈外腔中激光的偏振同光栅刻线平行,光栅反射面和光栅刻线垂直并可以调节光栅衍射的入射角使其满足Littrow结构的要求。从而优化光栅反馈获得窄线宽和较大的连续可调谐范围。

ECDL激光器工作在780 nm铷原子D2线附近,经过光学隔离器后,利用λ/2波片和偏振分束棱镜(PBS)分出合适功率用于构建稳频系统和测频系统。1)将22 μW的激光导入磁致二色性无调制稳频系统(Dichroic Atomic Vapor Laser Lock,DAVLL)[15-16],获得鉴频信号后可通过反馈控制光栅角度的压电陶瓷构成闭环稳频系统,当改变鉴频信号的直流偏置时还可微调频率锁定点的位置。通过对比饱和吸收光谱后就可使激光频率稳定在某一个铷原子饱和吸收峰上(实验中将激光器频率锁定在图2中87Rb原子D2线饱和吸收光谱的C23交叉线上)。2)测频系统由饱和吸收光谱和相敏检波构成,饱和吸收光谱可作为频率参考。如图2所示,以87Rb交叉线C13和C2378.5 MHz的频率间隔为参考来标定吸收峰的微分信号,微分信号电压同激光频率变化的标度因子为901 kHz/V。

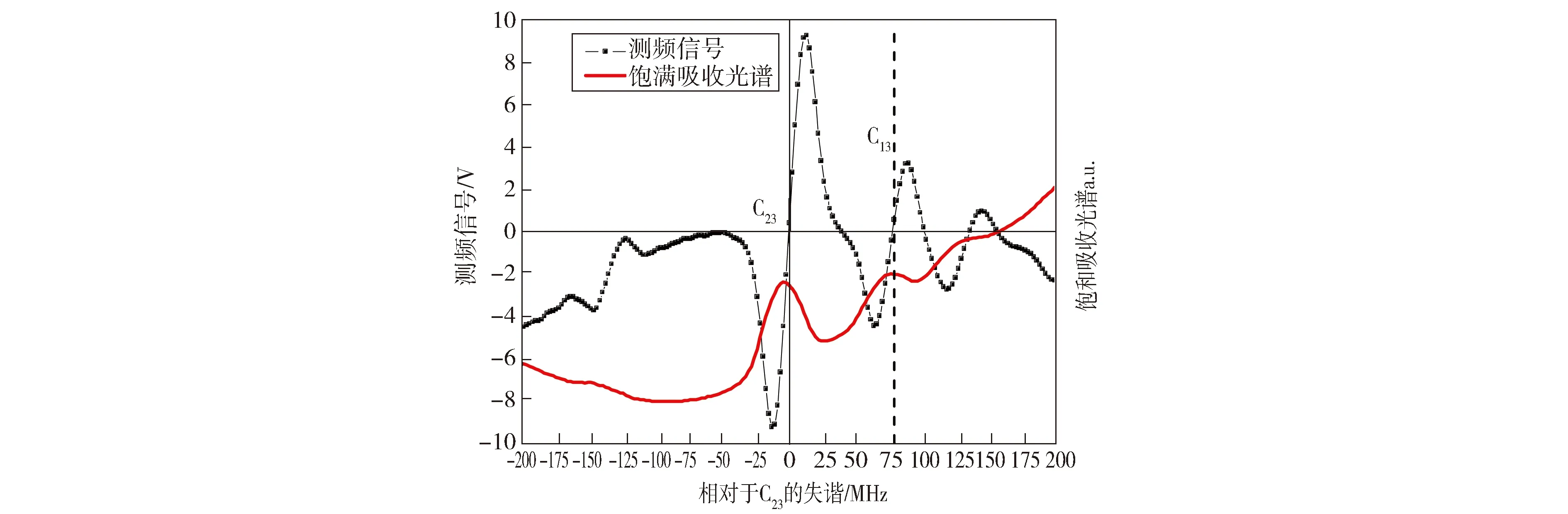
Fig.2 SAS of 87Rb D2line and frequency discriminating curve from PSD.The red solid line is the SAS from F=2 to F′=1、2、3, C23(C13)represent the crossover of the excited states F′=2 and F′=3 (F′=1 and F′=3). The black dot solid line is frequency discriminating curve via PSD from SR830. With the 78.5 MHz C23and C13 frequency interval,the scale factor 901 kHz/V of the frequency measurement system is calibrated图2 87Rb D2线的饱和吸收光谱和PSD获得的鉴频曲线。图中红色的实线是基态F=2到激发态F′=1、2、3的SAS,其中C23、C13分别表示到激发态F′=2和F′=3与F′=1和F′=3的交叉线。黑色的点实线由SR830锁相放大器经PSD获得的鉴频曲线。以C23、C13跃迁频率差78.5 MHz为频率参考标定鉴频曲线获得测频系统的标度因子为901 kHz/V

为了优化激光频率调制后测频系统的灵敏度和信噪比,实验上我们用到两个重要的工具:相敏检波(Phase Sensitive Detection, PSD)和快速傅里叶变换(Fast Fourier Transform,FFT)。PSD通过SRS公司的SR830锁相放大器来实现,检波需要的调制信号通过Thorlabs公司的LDC205C恒流源电流调制端口加载(电流调制带宽大于150 kHz),经过适当的相移并经乘法器和低通滤波后获得相敏检波信号,从而测量激光器输出频率在饱和吸收峰中心频率附近的频率变化。为了减小测频过程对稳频系统的干扰,PSD的调制频率需要远大于稳频系统的带宽,同时兼顾PSD信号的信噪比,选用68.77 kHz作为调制频率。原则上对激光器采用频率为ω的正弦电流调制,输出激光的频率就以频率为ω的正弦规律变化,相应PSD输出就是一个反映激光频率变化的正弦响应,通过示波器测量其振幅并对比相位差就可获得系统调制响应的增益和相移。为了处理实际系统除调制之外还存在的噪声,需要对系统调制输入的信号和由PSD获得的表征激光频率调制的信号都进行FFT频谱分析并对比,就可直观地获得开环或稳频系统闭环后激光器系统频率调制响应的幅频特性和相频特性。

2 激光器调频动态特性的测量

激光器系统的很多特性都会体现在输出频率的变化中,输出频率随着时间的变化源于系统的噪声和对输入的响应。虽然从时域上记录并分析系统的输出比较直观,但某些不确定性的系统干扰稍瞬即逝,某些微弱的干扰往往会淹没在噪声里,不利于进行分析。所以我们选择从频域上分析激光器系统输出频率被调制时的动态特性。测量激光器系统动态特性时,最直接的方法应该是分多次采用不同频率且振幅一致的点频正弦波作为调制信号,利用激光器恒流源的电流调制端口对输出激光进行频率调制,随后测量激光频率变化范围和频率变化同调制信号的相位关系,就可以获得该频率处激光频率调制的响应幅度和相移,从而获得激光器系统的幅频和相频动态响应特性。我们的激光器及其稳频系统带宽在kHz量级,理论上这些测试可以直接通过低频的网络分析仪或动态信号分析仪完成。由于ECDL激光器对调制电流非常敏感,电流工作点不合适容易存在跳模的问题,利用这些仪器时并不能很方便的选到合适的扰动信号,另一方面响应频率在低频区而且频率分辨率低于1 Hz的分析设备体积都很大,将来不可能同激光器系统一起配套。最终我们选用了可方便调节幅度的信号发生器提供输入,数字示波器(安捷伦MSO7104B)采集信号,FFT方法分析处理幅频特性和相频特性的方案。

本文数据处理中核心的问题是对激光频率的时变信号进行频域分析。实验上采集到的信号是离散的数据点,进行FFT分析需要考虑采样率fS和采样时间TS的选择。采样率是单位时间内的采样点数,所以采样点数N是采样率fS和采样时间TS的乘积。此时FFT分析的频率分辨率为采样时间的倒数,最高分析频率同单位时间的采样率有关,根据采样定理,为了保证采样信号不失真,采样率至少应该是信号特征频率的两倍,所以相邻两个数据点对应时间差倒数的一半就是最高分析频率。当采样时间1 s时,频率分辨率为1 Hz。当采样时间100 s时,频率分辨率可达到0.01 Hz。随着采样时间的增加,系统的频率分辨率也随之提高,但是对系统一致性要求很高。如果满足需要的最高分析频率,采样率不能变化,从而每一次测量数据量为采样时间乘以采样率就会急剧增加,导致对系统的测量效率降低。因此综合考虑测量效率、频率分辨率和最高分析频率的需求,最终选择采样时间为1 s,采样率为50 kHz,每个采样数据50 000个点,从而频率分辨率为1 Hz,最高分析频率为25 kHz。

我们知道利用lock-in相敏检波获得饱和吸收峰的微分信号作为频率测量的鉴频曲线只有在中心频率附近是接近线性的,所以调制信号的幅度不宜太大,要保障在线性范围内才能不失真测量。如果调制太强会产生明显的高阶谐波成分,调制太弱系统响应又容易被系统的噪声所淹没,最终选定点频正弦调制振幅为30 mV。

当频率为800 Hz振幅为30 mV的正弦波信号调制激光器的恒流源(恒流源调制因子为50 μA/mV)时,激光器稳频系统的响应如图3所示。其中图3(a)是20 ms时间范围内系统的输入和输出时域信号,图3(b)是对1 s时段的采样结果进行FFT分析后的频域信号。此时激光器的频率变化有两个特征频率,一个是正弦调制的频率,一个是相敏检波的调制频率(68.77 kHz已经大于FFT的最高分析频率)。此时在图3(b)中,还可以看到除过800 Hz外,系统还存在50 Hz及其高次谐波成分,这是市电信号扰动的影响。图中30 mV的调制获得的测频信号为3.23 V,这表明通过恒流源调制激光频率、锁相放大器测频后整个系统对调制电信号的增益为107.7。根据SAS标定的测频系统标度因子901 kHz/V,可知此时30 mV的调制信号可使激光频率调制范围为2.9 MHz,对应的频率调制系数为97 kHz/mV。

正弦点频响应测量需要多次用不同频率的正弦波调制激光器,其优点是直观反映系统的频率响应特性。但最大的缺点是需要多次测量,周期长,对系统稳定性要求高,而且数据也需要多次重复FFT的过程,工作量大。所以对于输入的调制信号,我们还探索了一种高效快速、更适用于测量激光器系统动态响应的周期性阶跃调制(方波)方案,并对其有效性进行了对比研究。

众所周知,方波包含非常丰富的频率成分,其傅里叶变换为:

其中A是方波信号的振幅,ω为信号的调制频率。显然方波各谐波的振幅随着阶次增加而衰减。它由一系列具有不同振幅,确定频率间隔的多个正弦单频信号构成。因此利用方波代替点频调制激光器,能同时实现多个频点的同步调制。

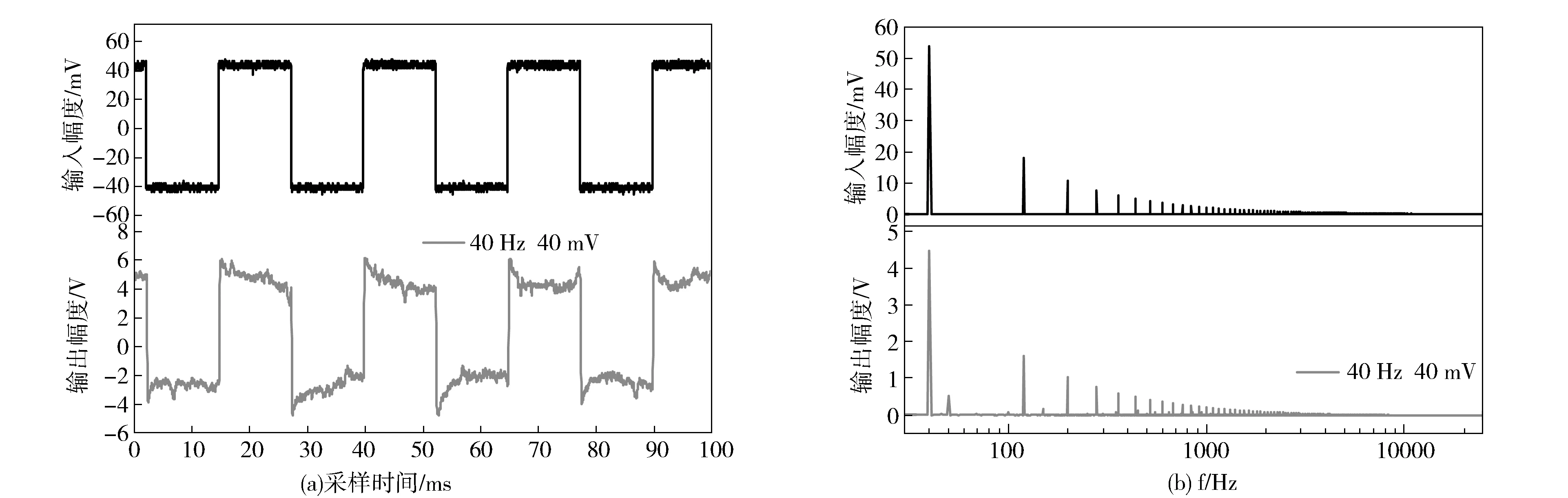
Fig.4 (a) Modulation signal(40 Hz and 40 mV, square wave) and the output from open-loop system(b) FFT frequency analysis of system modulation signal and output signal图4 (a)40 Hz,40 mV方波调制信号和开环系统的输出信号;(b)系统调制信号和输出信号的FFT频域分析

此时选择合适的方波振幅和频率是一个关键的问题。方波的频率如果太小,随着分析频率的增加,还没有到达系统带宽的范围,高阶谐波已被噪声淹没,不利于测量;如果频率太大,相邻两个谐波成分在频域上间隔太大,系统测量时频率分辨率过差。如果振幅太大,系统会超出鉴频曲线的线性响应区影响测量结果;如果振幅太小,高次谐波太弱,在高频区的频率响应同样容易被噪声淹没。最终确定以信号发生器DS345输出的频率40 Hz振幅40 mV的方波信号作为激光器恒流源调制端口的调制输入。如图4所示,激光器自由运转(开环)时的测量结果。其中(a)是输入、输出的时域信号,(b)为FFT频域分析结果。通过对比输出和输入各个谐波分量,可测得系统对不同阶次的谐波频率处的响应。各阶谐波在对应频率点处的输出与输入的振幅比就是系统的相对增益。如在40 Hz处相对增益为123,120 Hz处相对增益为118。从而可以得到对应频率点处系统的相对增益以及相对相移,并一次性获得整个闭环系统的频率响应特性。

3 结果与讨论

实验中选择一系列的不同频率的正弦波调制信号加到激光器的恒流源电流调制端口,分别用数字示波器采集测频系统获得的频率变化信号,经FFT频域分析后可以获得每个频点处对应的增益(输出信号振幅与调制输入信号振幅的比值)和相移(输入和输出信号的相对相位差),从而描绘出系统的幅频特性和相频特性曲线,如图5中黑色点线所示。在每次测量中改变正弦波的频率,分别记录了从1 Hz到20 kHz范围内的多个调制频率时的响应。如果采用频率为40 Hz、振幅为40 mV的方波对系统进行调制,一次性FFT分析就可获得多阶谐波处的增益和相移,于是可快速高效获得幅频特性和相频特性曲线,如图5绿色实线所示。显然通过方波调制信号对激光器动态特性进行测试的方案同多个正弦点频调制相比结果一致,而且测量效率高,由于需要的测量时间短,受系统的漂移影响也很小。实际测量的采样时间只有1 s,因此完全可忽略激光器系统自由运转的频率漂移,因此我们可方便地获得开环系统的动态响应特性。图5中红色虚线所示为开环时系统的幅频特性曲线。

图5中开环和闭环在约1 kHz以后幅频特性曲线重合,说明整个系统类似于一个低通滤波器件,我们可获得环路3 dB带宽为4.1 kHz,从而可以为技术上进一步提高闭环系统带宽提供实验测量依据。

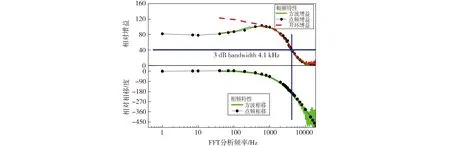
Fig.5 Dynamic response via the square wave and dot frequency method.The black dot solid line is the amplitude-frequency characteristic and phase-frequency characteristic of the closed-loop system with the dot frequency method. The green solid line is the response to square wave modulation.The red dash line is the amplitude frequency response of open-loop system to square wave modulation图5 方波和点频调制测量开环和闭环系统的幅频特性和相频特性。黑色点实线是多次正弦点频调制的测量结果,绿色的实线是方波的测量结果。红色的虚线是方波调制的方法测得的开环系统幅频特性

如果激光器系统足够稳定,动态特性测量系统的频率分辨率可简单通过提高采样时间来改善。对于闭环系统,两个频率接近的正弦波调制信号由信号发生器产生,同时输入到激光器恒流源的电流调制端口,振幅为25 mV、频率差为0.008 Hz(频率分别为110 Hz和100.008 Hz)。此时示波器的采样时间为500 s,采样点数为200万点,对应的最高分析频率为2 kHz,最高频率分辨率可达到0.002 Hz。如图6所示,可清晰的分辨两个频率调制信号,系统动态响应测试的频率分辨率可达0.002 Hz。

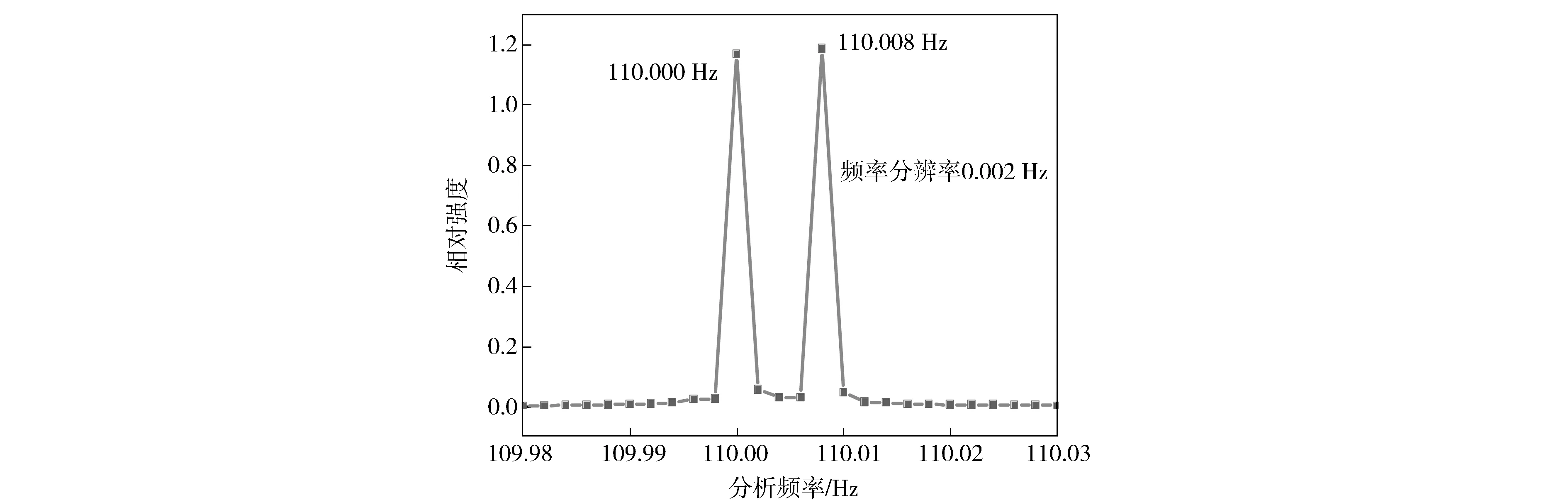
Fig.6 Dynamic characteristic of two sinusoidal modulation signals with frequency subtraction 0.008 Hz, the highest frequency resolution is 0.002 Hz图6 两个频率差为0.008 Hz正弦信号的调制特性,最高频率分辨率为0.002 Hz

我们知道激光器对工作环境的隔震、温度起伏、电磁屏蔽等都有很高的要求。科研实验室对这些因素一般都有很细致的处理措施。所以实验室的科研激光器系统几乎不可能直接应用于实际使用环境。这也是制约激光器广泛应用到实际工作中的瓶颈之一。本实验很重要的一个应用价值就是能够分析在恶劣环境中激光器系统被环境干扰的特征,从而可以据此对激光器的结构设计以及稳频反馈系统进行选择和优化。我们在实验室通过重物敲击实验平台,给激光器稳频系统引入机械冲击从而模拟了一个冲击环境。通过对比有无冲击时测频系统输出信号的差别,就可以研究闭环稳频激光器的冲击响应。

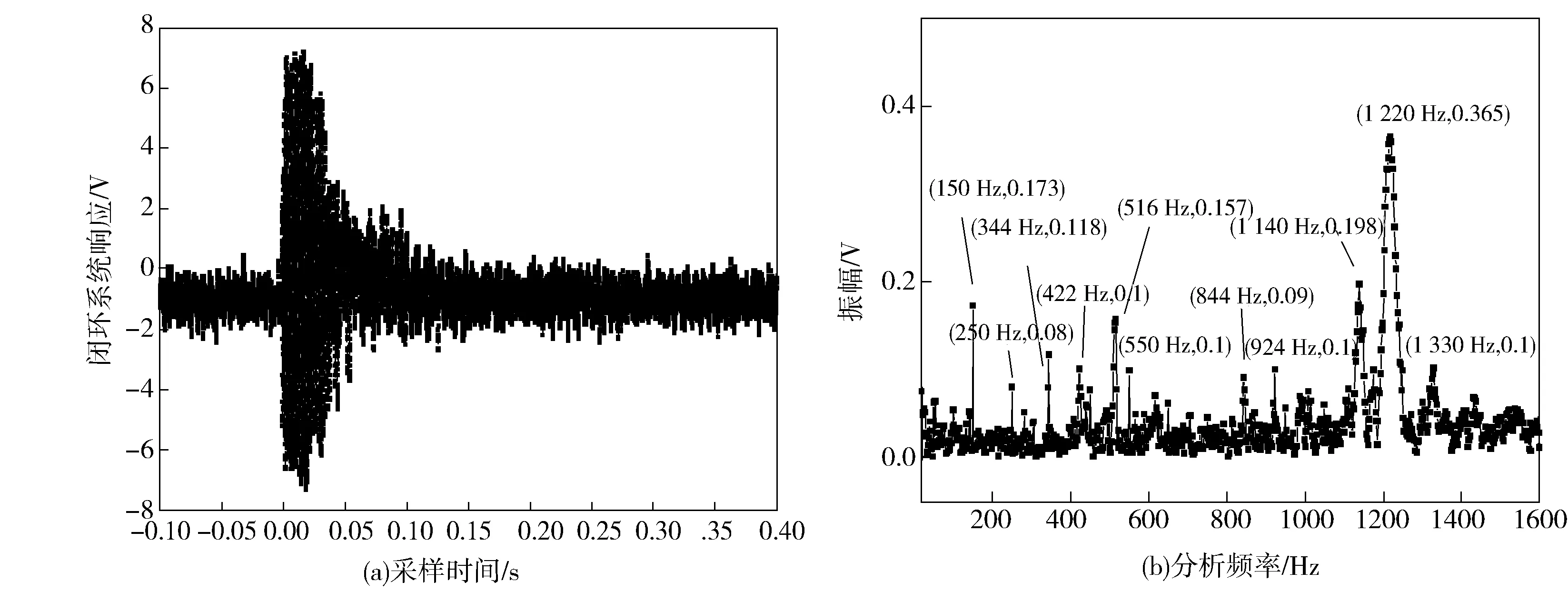
Fig.7 (a)Time domain response of the closed-loop system to mechanical shock (b)Frequency domain response of the closed-loop system to mechanical shock.图7 (a)闭环系统机械冲击下的时域响应;(b)闭环系统冲击响应的频域分析

在稳频系统经受机械冲击时激光频率变化如图7所示,可以看出存在多个频率成分的震荡。我们可以获知150 Hz、250 Hz和550 Hz是系统中固有的50 Hz市电及其高次谐波的干扰结果,而源于冲击的干扰中有344 Hz、422 Hz、516 Hz、844 Hz、924 Hz、1 140 Hz、1 222 Hz以及1 330 Hz等多个频率成分,其幅度各不相同。其中1 140 Hz和1 220 Hz是该冲击下激光频率扰动的主要成分。同时还可以看出冲击响应主要在300 Hz以上,在低于300 Hz的频段冲击导致的激光器频率没有明显的变化。这也能说明闭环稳频系统对于低频段的频率扰动有很好反馈校正能力。所以利用类似的方法分析外界特定环境的响应特点,可以为激光器面向比较恶劣的环境中工作,为提升激光器系统和稳频系统对外界环境抗干扰能力进行针对性的设计和优化提供参考。

4 结论

实验上利用外部信号经激光器的恒流源调制激光频率,构建测频系统后可测量激光频率的变化。测频系统可清晰的观测到间隔0.008 Hz的两个激光调制频率,测量的频率分辨率可优于0.002 Hz。利用测频系统可获得系统对多次正弦点频和方波调制信号的响应。系统的响应信号由示波器采集,经过FFT分析后获得幅频和相频特性。实验表明,本文采用的方波探测方案和正弦点频方案效果一致,而且测量效率高。在此基础上,利用本测量系统还重点研究了系统的冲击响应,获得冲击扰动的特征,其结果可为激光器在特定环境下进行针对性的闭环设计和参数优化提供依据。

[1] Ginzburg N S,Baryshev V R,Sergeev A S,et.al.Dynamics of Semiconductor Lasers with Two-dimensional Distributed Feedback[J].PhysRevA,2015,91:053806.DOI:10. 1103/PhysRevA.91.053806.

[2] Hanamaki Y,Kinoshita H,Akiyama H,et.al.Spontaneous-emission-lifetime Alteration in InxGa12xAs/GaAs Vertical-Cavity Surface-Emitting Laser Structures[J].PhysRevB,1997,56:R4379-R4382.DOI:10. 1103/PhysRevB.56.R4379.

[3] 黄蕾.用于腔与冷原子系综相互作用研究的整体腔光栅外腔反馈半导体激光器[D].太原:山西大学,2014:22-24.

[4] Dreve R W P,Hall J L,Kowalski F V,et.al.Laser Phase and Frequency Stabilization using an Optical Resonator[J].ApplPhysB,1983,31:97-105.DOI:10. 1007/AppliedPhysB.31.

[5] Kessler T,Hagemann C,Grebing C,etal.A Sub-40-mHz-linewidth Laser Based on A Silicon Single-crystal Optical Cavity[J].NaturePhotonics,2012,6:687-692.DOI:10. 1038/nphoton.2012.6.

[6] Schawlow A L，Townes C H.Infrared and Optical Masers[J].PhysRev,1958,112:1940-1949.DOI:10. 1103/PhysRev.112.1940.

[7] 刘润,蔡体菁,丁昊东.高精度石英挠性加速度计闭环系统的设计和分析[J].东南大学学报,2010,40:311-315.DOI:10. 3969/j.issn.40.311.

[8] Uchihashi T,Watanabe H,Fukuda S,et.al.Functional Extension of High-speed AFM for Wider Biological Applications[J].Ultramicroscopy,2016,160:182-196.DOI:10. 1016/j.ultramic.2015.10.017.

[9] Argencel B,Chanteau B,Lopez O,et.al.Quantum Cascade Laser Frequency Stabilization at the Sub-Hz Level[J].NaturePhotonics,2015,93:456-461.DOI:10. 1038/nphoton.2015.93.

[10] 瞿荣辉,蔡海文.高稳定度窄线宽激光器的研究[J].红外与激光工程,2009,38:1033-1038.DOI:10.3969/j.issn.38.1033.

[11] Evans M,Gras S,Fritschel P,etal.Observation of Parametric Instability in Advanced LIGO[J].PhysRevLett,2015,114:161102.DOI:10. 1103/PhysRevLett.114.161102.

[12] Vahlbruch H,Mehmet M,Danzmann K,etal.Detection of 15 dB Squeezed States of Light and Their Application for the Absolute Calibration of Photoelectric Quantum Efficiency[J].PhysRevLett,2016,117:110801.DOI:10. 1103/PhysRevLett.117.110801.

[13] Hall J,Taubman L,Ye J,etal.Laser Stabilization[M].America:McGraw Hill Professional,2001:27.1-27.4.

[14] 黄丹.高稳定ECDL系统及其动态特性研究[D].太原:山西大学,2016:7-8.

[15] Wang Junmin,Yan Shubin,Wang Yanhua,etal.Modulation-free Frequency Stabilization of A Grating-External-Cavity Diode Laser by Magnetically Induced Sub-Doppler Dichroism in Cesium Vapor Cell[J].JpnJApplPhys,2004,43:1168-1173.DOI:10.1143/JJAP.43.1168.

[16] Corwin K L,Lu Zhengtian,Hand C F,et.al.Frequency-stabilized Diode Laser with the Zeeman Shift in An Atomic Vapor[J].ApplOpt,1998,37:3295-3298.DOI:10. 1364/AO.37.003295.

DynamicResponseoftheGrating-FeedbackExternalCavityDiodeLaserandFrequencyStabilizationSystem

QIN Lijuan1,QIN Lin1,WANG Yanhua1,2*,WANG Junmin2,3

(1.SchoolofPhysicsandElectronicEngineering,ShanxiUniversity,Taiyuan030006,China;2.StateKeyLaboratoryofQuantumOpticsandQuantumOpticsDevices,andInstituteofOpto-Electronics,ShanxiUniversity,Taiyuan030006,China;3.CollaborativeInnovationCenterofExtremeOptics,ShanxiUniversity,Taiyuan030006,China)

Frequency stability is one of the key issues when the diode laser work in the harsh environment. The mechanical structure design of the laser should to be optimized. The corresponding calibration based for the environmental system characteristics is more crucial. So, in order to obtain the dynamic response of the ECDL laser and its frequency stabilization system, an efficient and precise method to measure laser frequency fluctuation is demonstrated. After recording the system response to sinusoidal and square wave modulation, the amplitude frequency and the phase frequency characters are obtained by Fast Fourier Transform. The results show that the measurement scheme of the square wave modulating signal is consistent with sinusoidal wave modulating signal, it is more effective and does not need multiple measurements. Using the dynamic analysis system, the response of closed-loop system to mechanical shock is achieved. It can provide the experimental basis for the calibration and optimization of the system parameters in the similar environment.

dynamic response;dynamic frequency character;external-cavity diode laser;laser frequency stabilization

10.13451/j.cnki.shanxi.univ(nat.sci.).2017.04.020

2017-01-20；

2017-02-22

国家自然科学基金(11374198);国家自然科学基金委国家重大科研仪器设备研制专项(61227902)

秦利娟(1991-),女,内蒙古乌兰察布人,硕士研究生,主要从事半导体激光技术和光与原子相互作用的研究。E-mail:942488066@qq.com

*通信作者：王彦华(WANG Yanhua),E-mail:wangyanhua@sxu.edu.cn

O437

A

0253-2395(2017)04-0789-08