纳米光纤腔中腔长诱导的相干动力学
张鸿宇,俞立先,汪丽蓉*
(1.山西大学 激光光谱研究所,量子光学与光量子器件国家重点实验室,山西 太原 030006;2.山西大学 极端光学协同创新中心,山西 太原 030006;3.绍兴文理学院 物理系,绍兴 312000)
纳米光纤腔中腔长诱导的相干动力学
张鸿宇1,2,俞立先3,汪丽蓉1,2*
(1.山西大学 激光光谱研究所,量子光学与光量子器件国家重点实验室,山西 太原 030006;2.山西大学 极端光学协同创新中心,山西 太原 030006;3.绍兴文理学院 物理系,绍兴 312000)
研究纳米光纤腔中光与二能级原子相互作用的相干动力学,该系统具有一个独特的特性:通过控制腔长将产生超强的光与原子相互作用。为了正确描述系统的相干动力学,首先推导出适合弱、强甚至超强相互作用下的Lindblad量子主方程。在此基础上,通过数值方法讨论了原子布居数、平均光子数和二阶关联函数。由于新得到的主方程考虑了反旋波作用,发现长时动力学和二阶关联展现出与传统主方程不一样结果。
纳米光纤腔;超强耦合;量子主方程
0 引言
近年来,具有亚波长直径的圆锥形光纤,即纳米光纤,在操控单原子、单光子等方面起到了重要的作用[1-5]。纳米光纤是由传统的光纤通过绝热方法使尖端变细所得,使得处于基本模式的光进入光纤的效率(渠道效率)超过百分之九十五[6-8]。在纳米光纤腔中,原子的自发辐射可以被大幅地抑制[9-10],而且其特殊的形状为俘获并探测少量原子带来了极大的便利[11-14]。纳米光纤腔在实现量子态的操控方面提供了很好的平台,并且为量子信息技术的发展开辟了新道路[15]。在腔量子电动力学的研究中,很重要的一部分工作是提高系统的相干性。提高相干性有很多方法,其中最直接的方法是提高腔和原子的耦合强度。
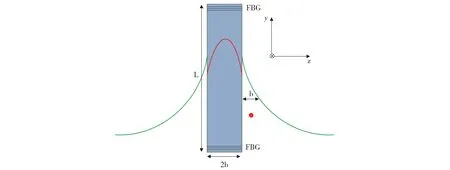
Fig.1 Schematic picture for the nanofiber cavity interacting with a two-level atom. The red and green solid curves show the intensity distributions of the intracavity and evanescent fields,respectively. b is the radius of the nanofiber, which is about 0.25 μm in experiments, and L is the tunable length of cavity. FBG denotes the Fiber Bragg grating. The nanofiber acts as a 1D photonic crystal cavity,and the atom (red point) is trapped upon the nanofiber surface红色和绿色的曲线分别表示纳米光纤腔和腔场的强度分布b表示纳米光纤腔的半径,实验上大约为0.25 μm;L为可调的腔长;FBG表示光纤光栅。这种结构可以把纳米光纤腔认为是一维光学腔,而且原子(红色点)被束缚在纳米光纤腔的表面图1 纳米光纤腔与等效二能级原子相互作用的示意图
考虑纳米光纤腔[16]和等效二能级原子的相互作用[17],如图1所示,它的哈密顿量[18-19]是
HR=ωa†a+ω0σ+σ-+g(a+a†)(σ-+σ+),
(1)
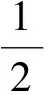
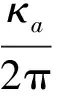
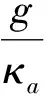
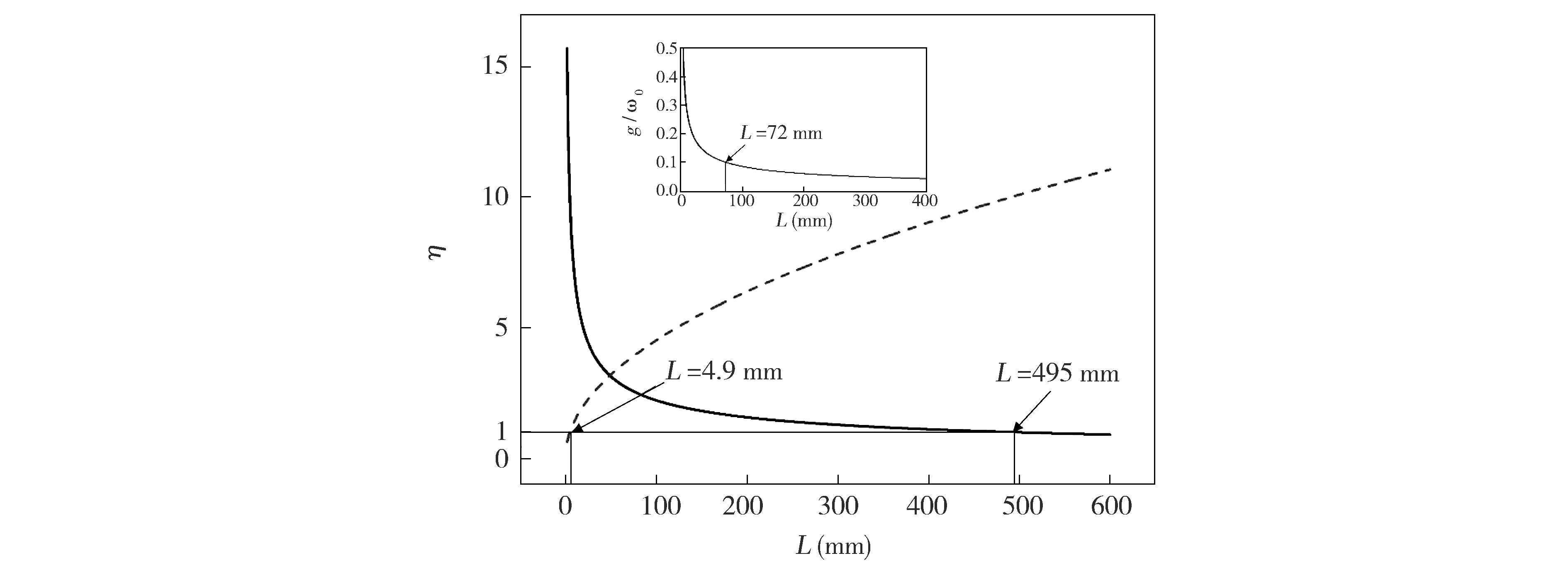
Fig.2 Plot the ratio of coupling strength and decay coefficient η with the change of nanofiber cavity length L.The solid line shows ,The dash line shows ,in which =6.1 MHz,ω=ω0=1 GHz,=0.01,F=500实线表示,虚线表示,其中,参数=6.1 MHz,ω=ω0=1 GHz,=0.01,F=500图2 耦合强度与耗散系数之间的比值η随纳米光纤腔长的关系
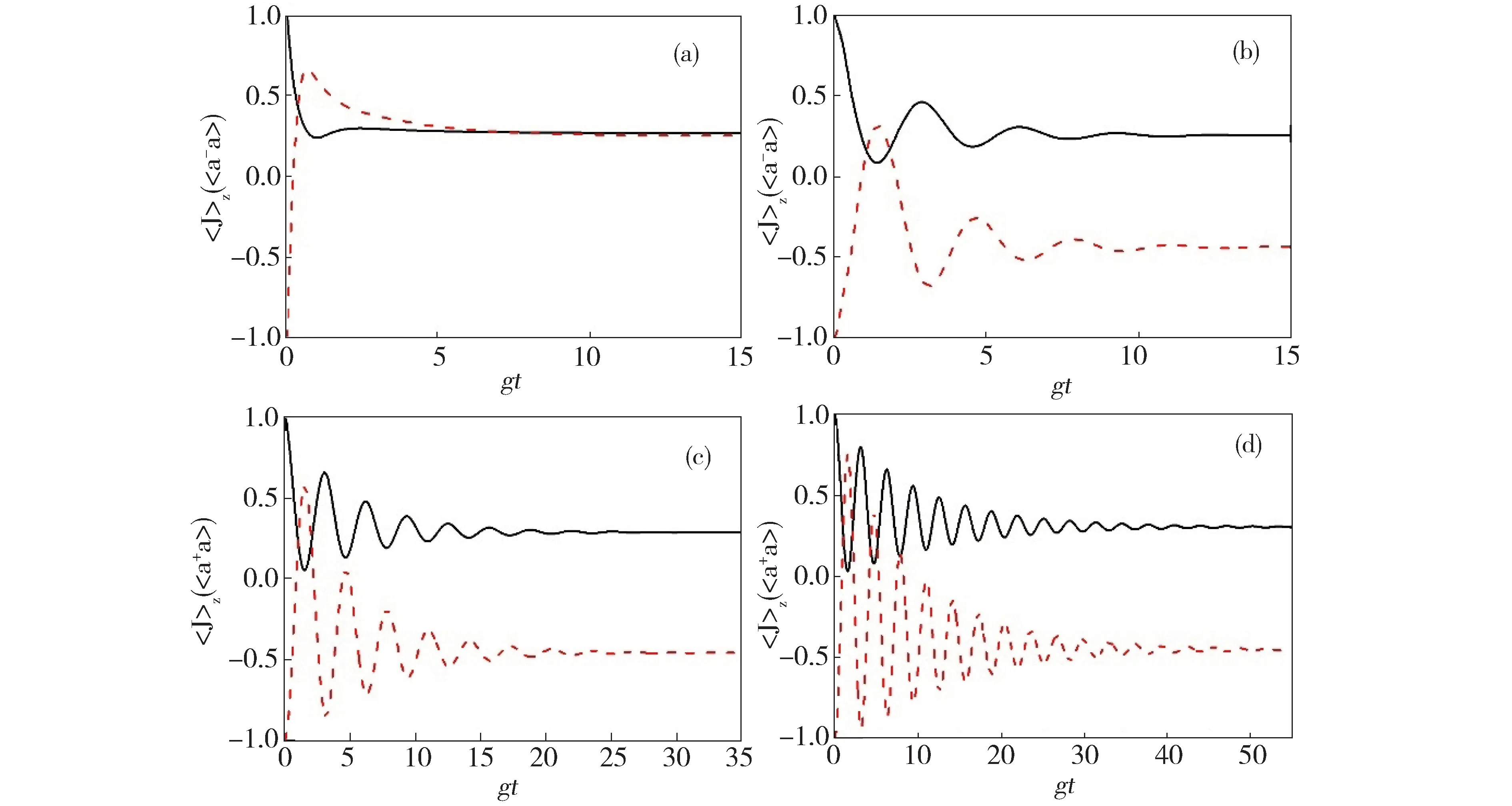
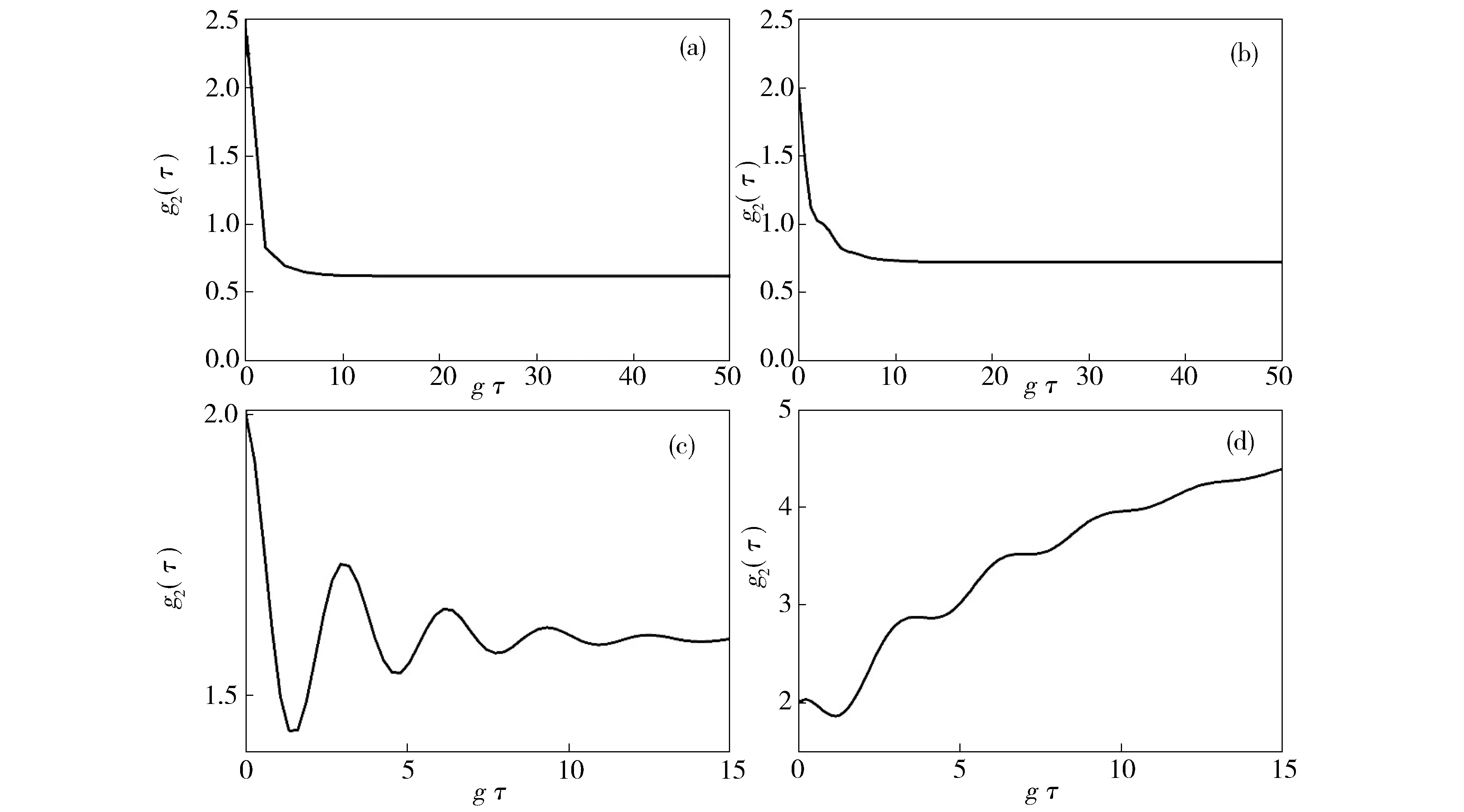
通过观察图2,能够清晰地看到通过纳米光纤腔腔长的变化,系统能够实现原子和光场的弱耦合、强耦合,甚至超强耦合。腔长短或者长的情况下,都只能实现弱耦合,但是短腔时主要由光场耗散占主导,而在长腔时原子耗散占主导。而在较大的腔长变化范围内,即4.9 mm 基于系统获得超强耦合的可能性,而耗散情况不能忽略,同时,Lindblad量子主方程适用于系统内弱耦合的情况,不能完全适用本系统。因此,需要能够描述超强耦合下耗散系统的新主方程。本文围绕上述问题,首先在理论上推导出在强耦合甚至超强耦合下依然适用的Lindblad量子主方程。接着借助数值法研究了纳米光纤腔的动力学行为,主要讨论了平均光子数和原子布居数随时间变化的相干动力学,以及光场二阶关联函数。通过理论和数值研究发现了传统的Lindblad主方程所不能预言的新结果。 如前所述,改变腔长能使二能级原子与光子的耦合强度实现弱耦合、强耦合甚至超强耦合。对于超强耦合的系统,由于与原子和光场相互作用所对应的反旋波项不能去除,通过旋波近似得到的Lindblad主方程将存在失效的可能,因此推导过程中需要保留反旋波项。 把纳米光纤腔和二能级原子看作为开放子系统S,该子系统与玻色库B构成一个封闭系统,其动力学可以用Liouville-von Neumann方程来描述 (2) 其中,ρSB是封闭系统的密度算符,H为封闭系统的总哈密顿量。一般情况下,总哈密顿量包含三个部分,即 H=HS+HB+HSB, (3) (2)式是在Schrödinger绘景下刻画封闭系统的动力学。为了计算简单,首先将其变换到相互作用绘景中,即 (4) 其中ρ(t)是在相互作用绘景中描述封闭系统的密度算符。假设初始时刻纳米光纤腔与二能级原子没有相互作用,我们对(4)式依次进行积分、迭代、求迹,得到 (5) 其中TrB表示对玻色库求迹。如果开放子系统与玻色库发生弱相互作用,并且忽略玻色库对开放子系统的影响,我们可以运用Born近似和Morkov近似[29-30]消除封闭系统的密度算符ρ(s),得到Redfield方程 (6) 在相互作用绘景中,哈密顿量HSB可以写成 (7) HSB=S(t)B†(t)+S†(t)B(t), (8) (9) 其中Lindblad超算符为 (10) (11) 在零温(T=0)情况下,(11)式变为 (12) (11)式和(12)式是我们需要的Lindblad主方程[31-32],它可以描述开放子系统在任意二能级原子和光子耦合强度(或者任意腔长)下的动力学问题。如果二能级原子和光子是弱耦合,可以忽略其反旋波项,此时可以分别考虑光子和二能级原子的耗散,对于腔内光子,|j〉〈k|即为湮灭算符a,而对于腔内二能级原子,|j〉〈k|即为σ-,因此主方程变为 (13) (13)式与我们熟知的弱耦合情况下的Lindblad主方程[33-36]形式是一致的。 对于满足超强耦合下的主方程(12)式在弱耦合情况下,相对于Lindblad主方程动力学行为的差异,主要来源于反旋波项。 Fig.3 Plot the numerical comparison of formula (12) and (13) in which g=κa=κp=ω0×10-3 and the initial state is |1〉⊗|↓〉.The red line shows the atomic population, the black line shows the average photon number, the solid line and dash line shows the dynamic behavior of formula (12) and (13) respectively取g=κa=κp=ω0×10-3,初始态为|1〉⊗|↓〉红线表示原子布居数,黑线表示平均光子数,实线和虚线分别代表(12)、(13)式刻画的动力学行为图3 弱耦合情况下(12)式和(13)式的数值比较 图3表示考虑超强耦合下反旋波项作用的主方程与弱耦合下主方程的区别,对于短时间演化两者具有相当好的吻合度,而当考虑长时动力学行为,两者又表现为较大的差异。这说明,在弱耦合情况下,即使在计算能谱方面可以通过旋波近似去除反旋波项,但是在动力学特别是长时动力学看来反旋波的作用不可忽略。至于哪种理论模型更适合于实际物理体系的描述,则需要更好的结合实验本身。 对于纳米光纤腔系统,其基本特征是原子和量子化光场的耦合强度g以及光场的耗散κp均受到腔长的限制,因此,研究不同腔长下的动力学具有一定的意义。下面我们主要考虑利用平均光子数和原子布居研究光纤腔系统相干动力学行为。 Fig.4 Plot the dynamic behaviors with different cavity lengths.(a) L=2 mm, (b) L=20 mm, (c) L=113 mm, (d) L=500 mm.The red line shows the atomic population,the black line shows the average photon number,in which =6.1 MHz,ω=ω0=1 GHz,=0.01 and F=500(a)L=2 mm,(b)L=20 mm,(c)L=113 mm,(d)L=500 mm。红色虚线表示原子布居数,黑色实线表示平均光子数,初始态为|1〉⊗|↓〉。其中,参数=6.1 MHz,ω=ω0=1 GHz,=0.01和F=500图4 纳米光纤腔不同腔长的动力学 图4中,我们取纳米光纤腔的长度(a)和(d)使系统处在弱耦合,(b)和(c)能够取得系统原子和光场之间超强耦合和强耦合。图4(a)中由于光场耗散、原子耗散与耦合强度之间满足κa 光强测量是光学中最为基本和重要的测量,借助关联函数能够反映系统的演化特征,二阶关联函数定义为 (14) Fig.5 Plot the second order correlation function g2(τ) with different cavity length.(a) L=2 mm, (b) L=20 mm, (c) L=113 mm, (d) L=500 mm.The parameter is =6.1 MHz,ω=ω0=1 GHz,=0.01,F=500 and T=0.45(a)L=2 mm,(b)L=20 mm,(c)L=113 mm,(d)L=500 mm。其中,参数为=6.1 MHz,ω=ω0=1 GHz,=0.01,F=500和T=0.45图5 不同纳米光纤腔长的二阶关联函数g2(τ) 从图5中可以看出,在光场耗散下占主导的光纤系统,不论弱耦合情况(a),还是超强耦合(b)在τ较小的时候g2(τ)>1呈现一种聚束效应,而在τ较大时候出现反聚束效应,即容易导致量子粒子数态。而在原子耗散占主导的光纤腔系统,不论处在强耦合情况(c),还是弱耦合(d),均出现聚束效应,也就是说光子更倾向于成对出现,并且对于(d)更容易导致g2(τ)>2。值得注意的是在有限温度的环境作用下,根据一般的Lindblad主方程会导致g2(0)=2[20],而根据(11)式则可以出现不同的情况,图5中(a)便是。 本文推导出了纳米光纤腔中适用于任何腔长的Lindblad量子主方程,并基于此方程,利用数值方法讨论了不同腔长时系统的动力学,并研究了二阶关联函数。由于新得到的主方程考虑了原子和光场的量子化反旋波作用,长时动力学行为与一般主方程有较大的不同,并且二阶关联函数与一般主方程预言也有不同的结果。 [1] Nayak K P,Melentiev P N,Morinaga M,etal.Optical Nanofiber as An Efficient tool for Manipulating and Probing Atomic Fluorescence[J].OptExpress,2007,15:5431-5438.DOI:10.1364/OE.15.005431. [2] Nayak K P,Hakuta K.Single Atoms on An Optical Nanofibre[J].NewJPhys,2008,10:053003.DOI:10.10881367-2630/10/5/053003. [3] Yalla R,Nayak K P,Hakuta K.Fluorescence Photon Measurements from Single Quantum Dots on An Optical Nanofiber[J].OptExpress,2012,20:2932-2941.DOI:10.1364/OE.20.002932. [4] Nayak K P,Zhang P F,Hakuta K.Optical Nanofiber-based Photonic Crystal Cavity[J].OL,2014,39:000232.DOI:10.1364/OL.39.000232. [5] Takashima H,Fujiwara M,Schell A W,etal.Detailed Numerical Analysis of Photon Emission from A Single Light Emitter Coupled with A Nanofiber Bragg Cavity[J].OE,2016,24:015050.DOI:10.1364/OE.24.015050. [6] Kien F L,Hakuta K.Cooperative Enhancement of Channeling of Emission from Atom Into Nanofiber[J].PhysRevA,2008,77:013801.DOI:10.1103/PhysRevA.77.013801. [7] Kien F L,Hakuta K.Intracavity Electromagnetically Induced Transparency in Atoms Around A Nanofiber with a Pair of Bragg Grating Mirrors[J].PhysRevA,2009,79:043813.DOI:10.1103/PhysRevA.79.043813. [8] Kien F L,Hakuta K.Cavity-enhanced Channeling of Emission from an Atom Into A Nanofiber[J].PhysRevA,2009,80:053826.DOI:10.1103/PhysRevA.80.053826. [9] Kien F L,Gupta S D,Balykin V I,etal.Spontaneous Emission of a Cesium Atom Near A Nanofiber:Efficient Coupling of Light to Guided Modes[J].PhysRevA,2005,72:032509.DOI:10.1103/PhysRevA.72.032509. [10] Yalla R,Kien F L,Morinaga M,etal.Efficient Channeling of Fluorescence Photons from Single Quantum Dots Into Guided Modes of Optical Nanofiber[J].PhysRevLett,2012,109:063602.DOI:10.1103/PhysRevLett.109.063602. [11] Kien F L,Balykin V I,Hakuta K.Scattering of An Evanescent Light Field by A Single Cesium Atom Near a Nanofiber[J].PhysRevA,2006,73:013819.DOI:10.1103/PhysRevA.73.013819. [12] Kien F L,Balykin V I,Hakuta K.Atom Trap and Waveguide Using A Two-color Evanescent Light Field Around a Subwavelength-diameter Optical Fiber[J].PhysRevA,2004,70:063403.DOI:10.1103/PhysRevA.70.063403. [13] Vetsch E,Reitz D,Sagúe G,etal.Optical Interface Created by Laser-cooled Atoms Trapped in the Evanescent Field Surrounding An Optical Nanofiber[J].PhysRevLett,2010,104:203603.DOI:10.1103/PhysRevLett.104.203603. [14] Goban A,Choi K S,Alton D J,etal.Demonstration of A State-insensitive,Compensated Nanofiber Trap[J].PhysRevLett,2012,109:033603.DOI:10.1103/PhysRevLett.109.033603. [15] Kimble H J.The Quantum Internet[J].Nature,2008,453:1023-1030.DOI:10.1038/nature07127. [16] Zhang Y W,Fan J T,Liang J Q,etal.Photon Devil’s Staircase:Photon Long-range Repulsive Interaction in Lattices of Coupled Resonators with Rydberg Atoms[J].SciRep,2015,10:1038/screp11510.DOI:10.1038/screp11510. [17] Dimer F,Estimnne B,Parkins A S,etal.Proposed Realization of the Dicke-model Quantum Phase Transition in An Optical Cativity QED System[J].PhysRevA,2007,75:013804.DOI:10.1103/PhysRevA.75.013804. [18] Steck D A.Quantum and Atom Optics[M].Eugene,Oregon 97403-1274,2012. [19] Scully M O,Zubairy M S.Quantum Optics[M].Cambridge University Press,1997:145. [20] Kien F L,Hakuta K.Cavity-enhanced Channeling of Emission from An Atom Into A Nanofiber[J].PhysRevA,2009,80:053826.DOI:10.1103/PhysRevA.80.053826. [21] Anapprar A A,Liberato D S,Tredicucci A,etal.Signatures of the Ultrastrong Light-matter Coupling Regime[J].PhysRevB,2009,79:201303.DOI:10.1103/PhysRevB.79.201303. [22] Bourassa J,Gambetta J M,Abdumalikov A,etal.Ultrastrong Coupling Regime of Cavity QED with Phase-biased Flux Qubits[J].PhysRevA,2009,80:032109.DOI:10.1103/PhysRevA.80.032109. [23] Ashhab S,Nori F.Qubit-oscillator Systems in the Ultrastrong-coupling Regime and Their Potential for Preparing Nonclassical States[J].PhysRevA,2010,81:042311.DOI:10.1103/PhysRevA.81.042311. [24] Niemczyk T,Deppe F,Huebl H,etal.Circuit Quantum Electrodynamics in the Ultrastrong-coupling Regime[J],NatPhys,2010,6:772.DOI:10.1038/NPHYS1730. [25] Hausinger J,Grifoni M.Qubit-oscillator System under Ultrastrong Coupling and Extreme Driving[J].PhysRevA,2011,83:030301.DOI:10.1103/PhysRevA.83.030301. [26] Kelvin M C,Law C K.Ground State of A Resonant Two-qubit Cavity System in the Ultrastrong-coupling Regime[J].PhysRevA,2013,88:015802.DOI:10.1103/PhysRevA.88.015802. [27] Huppert S,Vasanelli A,Pegolotti G,etal.Strong and Ultrastrong Coupling with Free-space Radiation[J].PhysRevB,2016,94:155418.DOI:10.1103/PhysRevB.94.155418. [28] Saiko A P,Markevich S A,Fedaruk R.Dissipative Two-level Systems Under Ultrastrong Off-resonant Driving[J].PhysRevA,2016,93:063834.DOI:10.1103/PhysRevA.77.013801. [29] Dicke R H.Coherence in Spontaneous Radiation Processes[J].PhysRev,1954,93:99.DOI:10.1103/PhysRev.93.99. [30] Carmichael H.An Open Systems Approach to Quantum Optics[M].Berlin Heidelberg New York,1991:5. [31] Irish E K.Generalized Rotating-Wave Approximation for Arbitrarily Large Coupling[J].PhysRevLett,2007,99:173601.DOI:10.1103/PhysRevA.99.173601. [32] Beaudoin F,Gambetta J M,Blais A.Dissipation and Ultrastrong Coupling in Circuit QED[J].PhysRevA,2011,84:043832.DOI:10.1103/PhysRevA.84.043832. [33] Ridolfo A,Savasta S,Harmann M J.Nonclassical Radiation from Thermal Cavities in the Ultrastrong Coupling Regime[J].PhysRevLett,2013,110:163601.DOI:10.1103/PhysRevLett.110.163601. [34] Breuer H P,Petruccione F.The Theory of Open Quantum Systems[M].Oxford University Press,New York,2002:109. [35] Lindblad G.On the Generators of Quantum Dynamical semigroups,Commun[J].MathPhys,1976,48:119.DOI:10.1007/BF01608499. [36] Michael A,Nielsen,Isaac L C.Quantum Computation and Quantum Information[M].Cambridge University press,2004:152. CoherentDynamicsInducedbytheCavityLengthintheNanofiberCavity ZHANG Hongyu1,2,YU Lixian3,WANG Lirong1,2* (1.InstituteofLaserSpectroscopy,ShanxiUniversity,Taiyuan030006,China; 2.CollaborativeInnovationCenterofExtremeOptics,ShanxiUniversity,Taiyuan030006,China; 3.DepartmentofPhysics,ShaoxingUniversity,Shaoxing312000,China) We investigate the coherent dynamics of the interaction between the photon and two-level atom in the nanofiber cavity,and this system has a distinct property that the ultrastrong photon-atom interaction can be generated by controlling the cavity length. In order to correctly describe the systematic dynamics, we first derive a generalized Lindblad equation, which is valid for the weak, strong and evenultrastrong photon-atom interaction. Based on this equation, the atom population, mean-photon number, and second-order correlated function are calculated numerically. Since the derived Lindblad equation consider the role of the counterrotating terms, the long-time coherent dynamics and second-order correlation exhibit different behaviors obtained in the conventional Lindblad equation. nanofiber cavity;strong coupling;lindblad master equation 10.13451/j.cnki.shanxi.univ(nat.sci.).2017.04.018 2016-12-07; 2017-01-11 国家自然科学基金(61575116);国家自然科学基金(61378049) 张鸿宇(1991-),女,山西吕梁人,硕士研究生。E-mail:Zhanghy911106@163.com *通信作者:汪丽蓉(WANG Lirong),E-mail:wlr@sxu.edu.cn O431 A 0253-2395(2017)04-0781-081 任意腔长下的Lindblad主方程
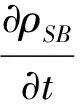
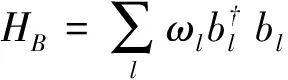
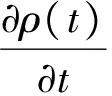



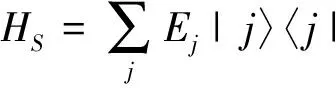
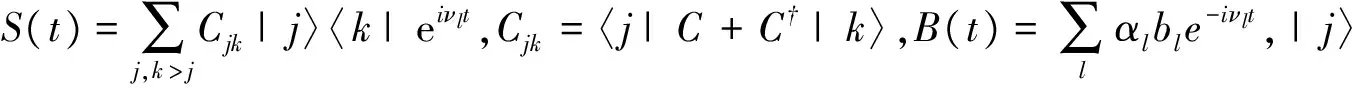

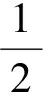
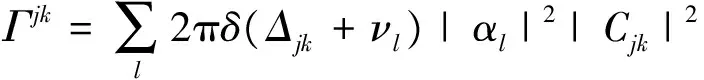



2 腔长诱导的相干动力学


3 结论

