超高维线性回归模型的一种方差估计
李济洪,闫文楠,王钰,杨杏丽
(1.山西大学 软件学院,山西 太原 030006;2.山西大学 数学科学学院,山西 太原 030006)
超高维线性回归模型的一种方差估计
李济洪1,闫文楠2,王钰1,杨杏丽2
(1.山西大学 软件学院,山西 太原 030006;2.山西大学 数学科学学院,山西 太原 030006)
超高维线性回归中的方差估计问题是超高维回归分析中需要解决的关键问题。针对在超高维线性回归中普通最小二乘法得到的方差估计存在有偏性的问题,有学者基于标准二折交叉验证提出了一种新的方差估计方法RCV。但发现方差的RCV估计依赖于数据的切分,稳定性差。为此,文章提出用组块3×2交叉验证的方法进行方差估计,并通过模拟实验将其与RCV方法进行了比较,验证了组块3×2交叉验证估计比RCV估计更为稳定。
超高维回归;数据切分;组块3×2交叉验证;方差估计
0 引 言
线性回归模型中的方差估计是回归分析中的基本统计推断问题之一。良好的方差估计是回归系数的置信区间、假设检验以及变量选择中的调节参数选择的基础。
对于一般的线性回归模型,传统的方差估计方法是:首先用AIC、BIC准则[1-2]进行模型选择,而后使用最小二乘法对所选变量的回归系数进行估计,最后使用残差平方和除以剩余自由度得到方差的估计,这种估计方法称为方差的最小二乘估计。在典型的线性回归模型下,方差的最小二乘估计是一致最小方差无偏估计。但是,在超高维线性回归中,即协变量的个数远大于样本量的情况下,会出现许多新问题[3-7]。Fan等(2012)[3], Stephen等.(2016)[4]的研究表明,按照上述过程得到的方差的最小二乘估计将会产生很大的偏差。
在超高维线性回归中的方差估计问题一般来说,需要稀疏性假设,也即虽然可选的变量很多(远大于样本个数),但真正在模型中起作用的变量的个数很少,要小于样本个数,使用传统的所有可能子集的变量选择办法是NP难问题,无法实现。Fan and Lv(2008)[8]针对超高维线性回归提出了SIS(sure independent screening)及ISIS(iteratively sure independent screening)变量选择方法[9-11]。SIS是根据协变量中与响应变量的相关系数大小先做一次筛选,将超高维线性回归的变量选择问题转化到一般的高维问题,再用通常的高维回归的处理方法,如Lasso(least absolute shrinkage and selection)和SCAD(smoothly clipped absolute deviation)等方法[12-22]。也即,需要先使用SIS 或ISIS将变量降到一定维数,使得变量维数接近样本量,然后再使用Lasso或SCAD方法估计回归系数。但Lasso或SCAD方法均依赖于模型的方差的估计,也就是在SIS选出变量后,就需要得到较好的方差估计。一个自然的想法就是在SIS后用方差的最小二乘估计。
然而,在使用SIS进行变量选择之后,Fan et al.(2012)[3]发现在超高维线性回归模型中,方差的最小二乘估计会产生很大的偏差,并且维数越高偏差越大。Fan et al.(2012)[3]分析认为,在超高维情况下,使用SIS做变量的初选后,选择的变量比较多,导致了一些不相关变量将被选入到模型中,此时基于同一数据集使用最小二乘估计回归系数得到残差,会造成对模型误差的严重低估,使得基于残差的方差估计有偏。为此,Fan et al.(2012)[3]提出了一种基于2折交叉验证的方差的RCV(refitted cross validation)估计方法,即将数据的一半用于SIS的变量选择,另一半对SIS选到的变量用于回归系数和方差的估计,大量的模拟实验验证了RCV能有效纠正方差的最小二乘估计的偏差。
为了提高方差估计的精度,Fan等(2012)[3]还建议对数据做多次对半切分,多次使用RCV估计,最后以多次的平均结果作为方差的估计。但是我们在实验过程中发现多次RCV的方差估计结果对数据的切分方式有较强的依赖性。在不同的数据切分下,RCV方差估计的结果相差较大。我们将通过一个模拟例子来说明这一点。具体地,采用空模型产生数据,在该模型中变量的系数均为0,其随机误差服从标准正态分布。该模型下的方差估计即为响应变量yi,i=1,2,…,n的方差。固定变量维数p=1 000,样本量n=60,用RCV方法进行方差估计。图1是当变量选择个数s=1和s=10时,不同切分下,用RCV进行方差估计得到的σ2密度图。
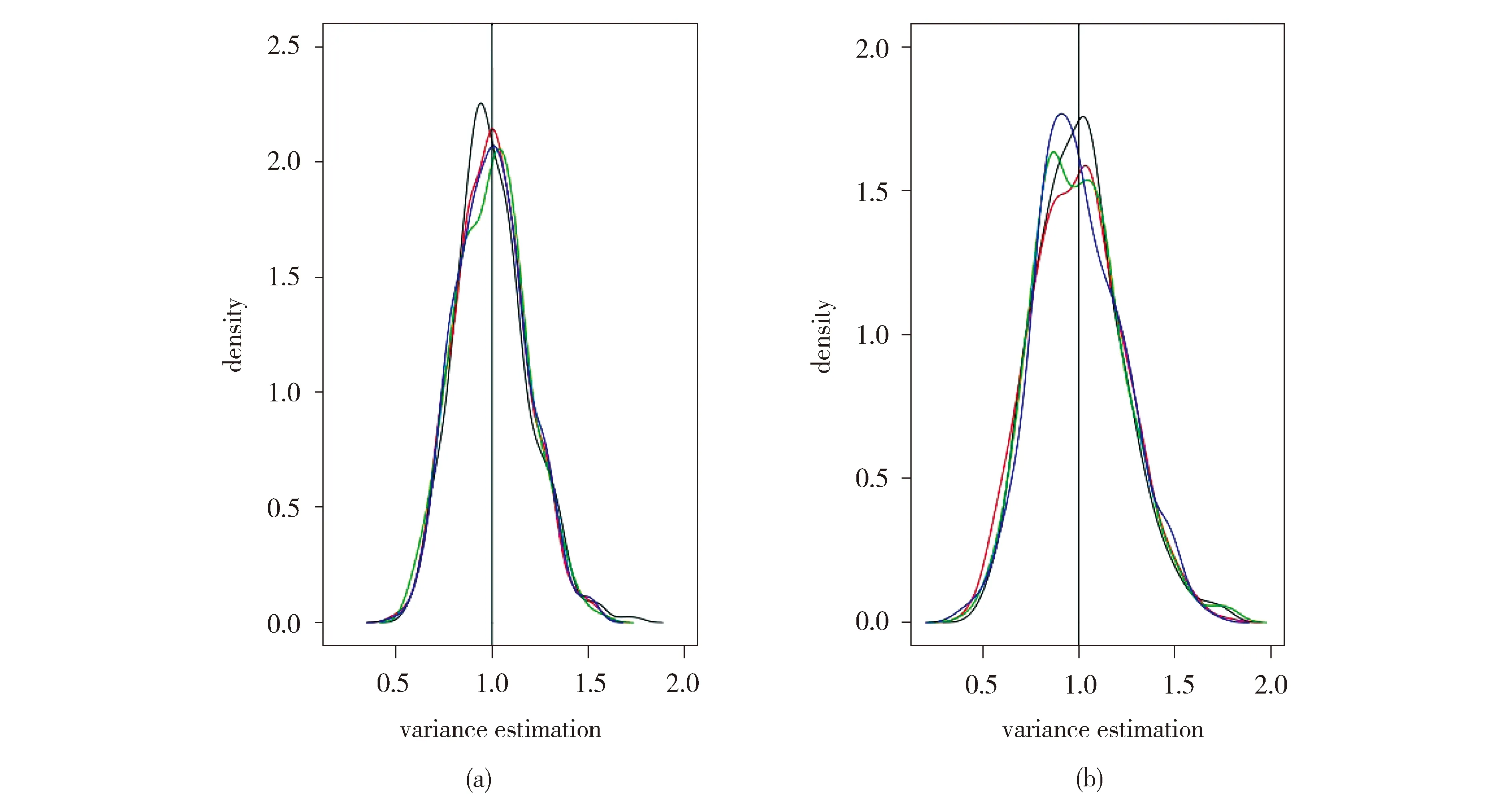
Fig.1 Densities of the variance estimations based on the RCV (a) for s=1 (b) for s=10 (lines with different colors represent different data partitioning;n=60,p=1 000,all calculations based on 500 simulations using SIS as a variable selector)图1 (a)、(b)分别表示,s=1,s=10 时,不同切分下,RCV方差估计的密度图(不同颜色的线条代表数据的不同的切分,所有实验结果均重复500次模拟且以SIS为变量选择方式,固定变量维数p=1 000,样本量n=60)
为了弱化数据切分对RCV的影响,我们考虑用组块3×2交叉验证(以下记为B3×2CV)的方法进行方差估计。Wang et al.(2014)[23]基于3次重复的2折交叉验证提出了B3×2CV,并证明了此方法应用于模型选择、泛化误差估计和算法性能对照检验中的优良性质[23-27]。为此,我们考虑使用B3×2CV来实施超高维线性回归中的方差估计问题。
1 超高维线性回归模型及方差估计方法
1.1 超高维回归模型及其记号
记超高维线性回归模型为
y=Xβ+ε
其中,y=(Y1,…,Yn)T是n×1维观测向量,X=(x1,…,xn)T是n×p(p≫n)设计矩阵,xi,i=1,2,…,n为p维向量。β=(β1,…,βp)T为p×1维回归系数向量,是未知参数。ε=(ε1,…,εn)T是误差向量,ε1,…,εn独立同分布,且E(εi)=0,var(εi)=σ2,所谓的方差估计即是对σ2的估计。
1.2 方差σ2的RCV估计
Fan et al.(2012)[3]给出了方差的RCV估计,具体步骤如下:
第一步:将数据随机地分成大致相等且不相交的两部分,记为(y1,X1),(y2,X2);
(一)精神迷乱。精神状态是刑事案件中最被关注的方面。英国是世界上最先关注罪犯精神状态的国家,1265年,英国政府颁布了著名野兽条例,该条例让患有精神障碍者不受法律制裁。1326年,政府也出台了相关法律,规定被告可以精神失常(包括非精神状态的人的无意识行为)为法定辩护理由来免除其刑事责任。这些都可以引起无罪的辩护。而《1800年刑事精神病法》明确了精神错乱的概念,这直接促成了1843年的“姆纳坦规则”。这些都可使具有精神障碍的人免除刑事司法的处罚。
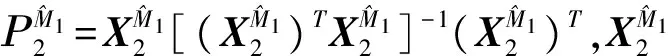
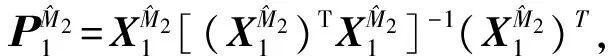
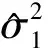
为了提高方差估计的精度,Fan et al.(2012)[3]还建议对数据做多次对半切分,多次使用RCV估计,最后以多次的结果的平均作为方差的估计。但是多次RCV的方差估计结果对数据的切分方式有较强的依赖性。由于多次随机数据切分,导致任意两次数据切分之间重叠的样本个数差异可能较大,使得方差的RCV估计的结果不稳定。
1.3 方差σ2的B3×2CV估计
Wang et al.(2014)[23]所提到B3×2CV如下。
先将数据集D均匀地分为大致相等且不相交的四个子集,记为Lj,j=1, 2, 3, 4。然后将四个子数据集两两组合,组成3组6个不同的组合,分别为:组别1:{(L1,L2), (L3,L4)};组别2:{(L1,L3), (L2,L4)};组别3:{(L1,L4), (L2,L3)}。在每一组上做一个标准的2折交叉验证,最后把3组2折交叉验证的结果进行平均。
Wang et al.(2017)[27]已经证明,B3×2CV的优势在于任意两组2折交叉验证的两个数据集的重叠样本个数均为样本个数的1/4,减少了随机切分带来的估计误差。因此,我们选用B3×2CV来看是否可以改善方差的估计。

以下给出B3×2CV的详细步骤。
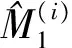
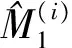
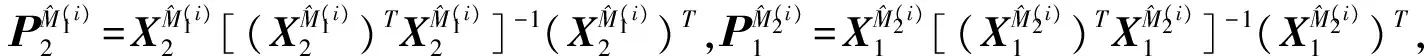
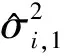
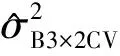
注:事实上,B3×2CV是一种特殊的3×2交叉验证。只是在B3×2CV中,任意两个训练集有相同数量的重叠样本。为了区分,我们把基于随机3次2折交叉验证的方差估计方法记为随机3×2交叉验证(以下记为R3×2CV)。随后,在以下实验中,我们将通过模拟实验将RCV,R3×2CV及B3×2CV若干估计进行对比。
2 模拟实验
本节基于模拟实验,将RCV估计与本文采用的B3×2CV估计进行比较。首先描述了实验的设置,接着对实验结果进行了分析。
2.1 实验一
为了便于比较,我们采用与Fan et al.(2012)[3]第一部分类似的实验设置,假设真实的数据产生于模型:
Y=XT0+ε,εi~N(0, 1)
其中x1,x2,…,xp是独立同分布的随机变量,且服从标准正态分布,并假设误差项与随机变量相互独立。取样本量n=60,变量的维数p=1 000。实验一基于SIS变量选择法,分别用RCV和B3×2CV进行方差估计。
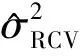
图2(a)、(b)分别是基于以上实验设置,RCV和B3×2CV方差估计的密度对比图。
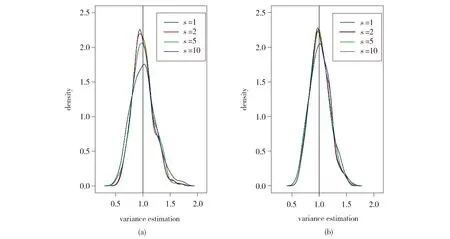
Fig.2 Densities of the variance estimations based on the RCV (a) and B3×2CV (b)(n=60, p=1 000;all calculations based on 500 simulations using SIS as a variable selector)图2 (a)为RCV方差估计的密度图,(b)为B3×2CV方差估计的密度图(均取样本量n=60,变量维数p=1 000,以SIS为变量选择方法,对于不同的s均重复500次模拟)
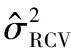
表1 实验一中和的方差对比Table 1 Variances of σ and σ for example 1
2.2 实验二
我们在更为复杂的模型下,将两种方法进行对比。选用Fan et al.(2012)[3]模拟实验部分的模型(18)
Y=b(X1+X2+X3)+ε,εi~N(0, 1)
真实的系数b=1,且Xi~N(0, 1),corr(Xi,Xj)=0.5,(i≠j;i,j=1, 2,…,p),n=200,p=2 000。我们选取变量的个数为s=80,基于SIS变量选择法比较了不同切分下的RCV和B3×2CV的估计结果,如图3所示。对比图3中各估计量的箱线图可以发现,无论是何种切分,其对应的RCV箱线图的四分位距均比R3×2CV及B3×2CV箱线图的四分位距宽,且其RCV箱线图正常值范围也比R3×2CV及B3×2CV箱线图正常值范围广,这均说明RCV方差估计的分布较为分散,波动大。而B3×2CV,我们从图上可以看出,虽然稍有一些偏差,但是它的四分位距和正常值范围最小,这说明B3×2CV方差估计的分布最为集中,也最稳定。
同样,我们计算了实验二中不同方法下得到的估计量的方差,并将其结果呈现于表2中。从表2可以发现不同切分下的RCV估计量的方差相差较大,其值波动在(0.042 8,0.077 8),且均大于B3×2CV估计量的方差0.027 3。R3×2CV估计量的方差虽比所有RCV估计量的方差小,但它仍大于B3×2CV估计量的方差,这说明B3×2CV估计比R3×2CV及RCV估计都稳定。
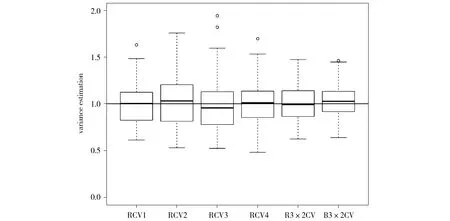
Fig.3 Boxplots of RCV with different partitions (RCV1, RCV2, RCV3, RCV4), R3×2CV and B3×2CV (all calculations based on 100 simulations using SIS as a variable selector)图3 不同切分下的RCV(RCV1,RCV2, RCV3, RCV4)、R3×2CV与B3×2CV估计的的箱线图(该图中所有的实验结果均为重复100次模拟所得)

表2 实验二中不同切分下的RCV的估计量与R3×2CV,B3×2CV的估计量的方差对比Table 2 Variances of RCV (with different data partitioning), R3×2CV, B3×2CV estimation for example 2
3 结论与展望
本文提出基于B3×2CV进行超高维线性回归中的方差估计,并通过模型实验验证了B3×2CV方法比RCV及R3×2CV方法更加稳定。本文主要是在SIS选变量后,直接用最小二乘估计回归系数,再用残差来估计方差。除此之外,可以考虑用回归系数的其他估计方法,如:岭回归等。在用岭回归下,B3×2CV的方差估计结果会如何呢?另外,基于SIS之后,得到初步的方差估计,再迭加使用其他的变量选择方法,如Lasso, SCAD, and Dantzig等,得到新的变量选择结果,再使用B3×2CV是否同样也会有较好的结果?上述这些问题,都值得我们今后进一步去研究。
[1] David G K,Lawrence L K,Keith E M,etal.Applied Regression Analysis and Other Multivariable Methods(Third Edition)[M].China Machine Press,2003.
[2] Kutner M H,Nachtsheim C,Neter J.Applied Linear Regression Models (Fourth Edition)[M].Mc Graw Hill Education,2005.
[3] Fan J,Guo S.Variance Estimation using Refitted Cross Validation in Ultrahigh Dimensional Regression[J].JRStatistSocB,2012,74:37-65.DOI:10.1111/.1467-9868.2011.01005.x.
[4] Stephen R,Robert T,Jerome F.A Study of Error Variance Estimation in Lasso Regression[J].StatistSin,2016,26:35-67.DOI:10.5705/ss.2014.042.
[5] Yang Y,Pan G.Independence Test for High Dimensional Data based on Regularized Canonical Correlation Coefficients[J].AnnStatist,2015,43(2):467-500.DOI:10.1214/14-AOS1284.
[6] Lai R C S,Hanning J,Lee T C M,etal.Generalized Fiducial Inference for Ultrahigh-dimensional Regression[J].JASA,2015,110:760-772.DOI:10.1080/01621459.2014.931237.
[7] Fan J,Li Q,Wang Y.Estimation of High Dimensional Mean Regression in the Absence of Symmetry and Light Tail Assumptions[J].JRStatistSocB,2017,79:247-265.DOI:10.1111/rssb.12166.
[8] Fan J,Lv J.Sure Independence Screening for Ultrahigh Dimensional Feature Space (with Discussion)[J].JRStatistSocB,2008,70:849-911.DOI:10.1111/j.1467-9868.2008.00674.x.
[9] Fan J,Samworth R,Wu Y.Ultrahigh Dimensional Feature Selection:Beyond the Linear Model[J].JMachLearnRes,2009,10:2013-2038.
[10] Fan J,Song R.Sure Independence Screening in Generalized Linear Models with NP-dimensionality[J].AnnStatist,2010,38:3567-3604.DOI:10.1214/10-AOS798.
[11] Fan J,Lv J.A Selective Overview of Variable Selection in High Dimensional Feature Space[J].StatistSin,2010,20:101-148.
[12] Kim Y,Choi H,Oh H S.Smoothly Clipped Absolute Deviation on High Dimensions[J].JAmStatistAss,2008,103:1665-1673.DOI:10.1198/016214508000001066.
[13] Lv J,Fan Y.A Unified Approach to Model Selection and Sparse Recovery using Regularized Least Squares[J].AnnStatist,2009,37:3498-3528.DOI:10.1214/09-AOS683.
[14] Meinshausen N,Yu B.LASSO-type Recovery of Sparse Representations for High-dimensional Data[J].AnnStatist,2009,37:246-270.DOI:0.1214/07-AOS582.
[15] Meier L,Van de Geer S,Bühlmann P.The Group Lasso for Logistic Regression[J].JRStatistSocB,2008,70:53-71.DOI:10.1111/j.1467-9868.2007.00627.x.
[16] Zhao P,Yu B.On Model Selection Consistency of Lasso[J].JMachLearnRes,2006,7:2541-2563.
[17] Zhang C H,Huang J.The Sparsity and Bias of the Lasso Selection in High-dimensional Linear Regression[J].AnnStatist,2008,36:1567-1594.DOI:10.1214/07-AOS520.
[18] Bunea F,Tsybakov A,Wegkamp M.Sparsity Oracle Inequalities for the Lasso[J].ElectronJStatist,2007,1:169-194.DOI:org/10.1214/07-EJS008.
[19] Candes E,Tao T.The Dantzig Selector:Statistical Estimation when p is Much Larger Than n (With Discussion)[J].AnnStatist,2007,35:2313-2351.DOI:10.1214/009053606000001523.
[20] Fan J,Peng H.Non-concave Penalized Likelihood with a Diverging Number of Parameters[J].AnnStatist,2004,32:928-961.DOI:10.1214/009053604000000256.
[21] Fan J,Lv J.Non-concave Penalized Likelihood with NP-dimensionality[J].IEEETransInformTheor,2011,57:5467-5484.DOI:10.1109/TIT.2011.2158486.
[22] Zhou X,Liu G.LAD-Lasso Variable Selection for Doublely Censored Median Regression Models[J].CommunicationsinStatistics—TheoryandMethods,2016,45:3658-3667.DOI:10.1080/03610926.2014.904357.
[23] Wang Y,Wang R,Jia H,etal.Blocked 3×2 Cross-validatedtTest for Comparing Supervised Classification Learning Algorithms[J].NeuralComputation,2014,26(1):208-235.DOI:10.1162/NECO-a-00532.
[24] Li J,Hu J,Wang Y.Blocked 3×2 Cross Validation Estimator of Prediction Error-A Simulated Comparative Study based on Biological Data[J].JournalofBiomathematics,2014,29(4):700-710.
[25] Li J,Wang R,Wang Y,etal.Automatic Labeling of Semantic Roles on Chinese Framenet[J].JournalofSoftware,2010,30(4):597-611.DOI:10.3724/SP.J.1001.2010.03756.
[26] Yang X,Wang Y,Wang R,etal.Variance of Estimator of the Prediction Error based on Blocked 3×2 Cross Validation[J].ChineseJournalofAppliedProbabilityandStatistic,2014,30(4):372-38.DOI:10.3969/j.issn.1001-4268.2014.04.004.
[27] Wang R,Wang Y,Li J,etal.Block-regularized m×2 Cross-validated Estimator of the Generalization Error[J].NeuralComputation,2017,29(2):519-554.DOI:10.1162/NECO-a-00923.
AnEstimatorofVarianceinUltrahighDimensionalLinearRegression
LI Jihong1,YAN Wennan2,WANG Yu1,YANG Xingli2
(1.SchoolofSoftware,ShanxiUniversity,Taiyuan030006,China;2.SchoolofMathematicalSciences,ShanxiUniversity,Taiyuan030006,China)
Variance estimation in ultrahigh dimensional linear regression is a key problem of regression analysis. In view of the biasedness of variance estimator based on ordinary least square, a new variance estimator based on a standard 2-fold cross-validation is proposed, denoted as RCV (refitted cross validation). However, the RCV estimator of variance (severely) relies on the data partitioning, and it easily results in poor stability. Thus, a variance estimator based on blocked 3×2 cross-validation is proposed.The simulated comparisons further demonstrate that the variance estimator based on blocked 3×2 cross-validation is more stable than that of RCV.
ultrahigh dimensional regression;data partitioning;blocked 3×2 cross-validation;variance estimation
10.13451/j.cnki.shanxi.univ(nat.sci.).2017.04.009
2017-03-13;
2017-04-19
国家社会科学基金(16BTJ034)
李济洪(1964-),男,山西长治人,博士,教授,主要研究方向:统计机器学习、自然语言处理。E-mail:lijh@sxu.edu.cn
O212
A
0253-2395(2017)04-0725-07

