Adaptive protograph-based BICM-ID relying on the RJ-MCMC algorithm: a reliable and efficient transmission solution for plasma sheath channels
Yanming LIU (刘彦明), Hailiang WEI (魏海亮), Lei SHI (石磊),∗and Bo YAO (姚博)
1 Key Laboratory of Information and Structure Efficiency in Extreme Environment, Ministry of Education of China, Xi’an 710071, People’s Republic of China
2 School of Aerospace Science and Technology, Xidian University, Xi’an 710071, People’s Republic of China
Abstract For reentry communication, owing to the influence of the highly dynamic plasma sheath (PS),the parasitic modulation effect can occur and the received phase shift keying (PSK)signal constellation can be severely rotated, leading to unacceptable demodulation performance degradation.In this work, an adaptive non-coherent bit-interleaved coded modulation with iterative decoding(BICM-ID)system with binary PSK(BPSK)modulation and protograph lowdensity parity-check under the PS channel is proposed.The proposed protograph-based BICMID(P-BICM-ID)system can achieve joint processing of demodulation and decoding,where the soft information is adaptively estimated by reversible-jump Markov chain Monte Carlo (RJMCMC)algorithms.Simulation results indicate that compared to existing algorithms, the proposed system can adapt well to the dynamic characteristics of the PS channel and can obtain a 5 dB performance improvement at a bit error rate of 10-6.
Keywords: plasma sheath, BICM-ID, Markov model, joint demodulation and decoding
1.Introduction
Due to the wide application prospects of hypersonic vehicles in civil and military fields, research on the communication technology of hypersonic aircraft has attracted widespread attention.However,when reentering or moving in the atmosphere at a speed exceeding Mach 8,the vehicle will be surrounded by a plasma layer (also called the plasma sheath)[1, 2], which can attenuate electromagnetic(EM)waves.The plasma sheath(PS)channel presents highly dynamic and non-stationary characteristics [3, 4] with parasitic modulation effects [5].These effects seriously affect the quality of reentry communication and can even cause radio blackouts [6-9].The problem of radio blackouts has not been completely solved yet.
Many methods have been developed to mitigate communication blackouts by lowering the PS electron density [10-12],such as aerodynamic shaping [13], liquid quenchant injection[14], and electromagnetic windowing [15, 16].However, the practical shortcomings and engineering obstacles of these methods have not been satisfactorily resolved.A probably feasible solution,aiming at adapting to the high dynamics and large-scale fading characteristics of the plasma sheath channel, is to design adaptive communication methods to alleviate communication blackout,such as increasing transmitted power or communication frequency [17], employing low-frequency communication [18],channel prediction relied on the reflected waves [19], and usingan adaptive data rate control method based on the antenna voltage standing wave ratio(VSWR)[20].Regarding modulation and demodulation methods over the PS channel, [21] and [22]investigated the performance of traditional modulation methods over the PS channel from theoretical and experimental perspectives, respectively.Research has shown that non-coherence frequency shift keying (NC-FSK)is better than phase-shift keying(PSK)and amplitude shift keying(ASK)modulations.Owing to the parasitic modulation effect, PSK modulation over the PS channel presents a great challenge.To address this problem,Yang et al proposed a novel demodulation method based on spectral clustering for PSK signals over the PS channel[23].Liu et al developed a joint demodulation and estimation algorithm based on a Bayesian learning method for extracting curves on the signal constellation and identifying the transmitted symbols[24].

Table 1.Typical values of Ne ( z , t).
However, these existing methods rarely involve coding schemes, nor do they exploit joint processing techniques for signal detection and decoding.Due to the non-stationary nature of PS channels, the performance improvement of these methods is limited.In fact, in many communication scenarios, the joint processing technique for signal detection and decoding can yield joint gains in addition to coding gains,and the LDPC-BICM-ID system[25-28]has been proved to be very effective and popular.Bit-interleaved coded modulation and iterative decoding(BICMID), which practically utilize iterative information exchange between the demodulator and the channel decoder while obtaining knowledge of other bit values, can achieve highly reliable wireless communication.The application of an interleaver in BICM-ID can also address sudden changes in the channel.Therefore,the LDPC-BICM-ID system can adapt to deep fading and dynamic channels.Note that the PS channel is just a kind of deep fading and highly dynamic channel.PSK and quadrature amplitude modulation (QAM)are widely used in LDPC-BICMID systems.However,high-order PSK modulations with poor bit error rate(BER)performance are difficult to apply to PS channels.Therefore,to achieve highly reliable and efficient communication performance under the PS channel, the LDPC-BICM-ID system based on binary PSK (BPSK)may be a feasible solution.
Low-density parity-check (LDPC)codes [29, 30] and protograph codes[31,32]have been extensively researched and combined with BICM-ID systems over many channels,such as fast-fading,block-fading,and satellite communication channels.However, designing an adaptive BICM-ID system over the PS channel remains a challenge.This is because PS channels possess a parasitic modulation effect and non-stationary characteristics, and the prior probability density function of the received signal is unknown.Thus, the soft information for maximum a posteriori (MAP)detector cannot be accurately calculated.
Against this background,an adaptive modified protographbased BICM-ID (P-BICM-ID)framework with BPSK modulation for PS channels is proposed.The main contribution of this work is that an adaptive soft information estimation method based on reversible-jump Markov chain Monte Carlo (RJMCMC)for our P-BICM-ID system is developed to calculate the soft information.Considering the uncertainty of the prior channel information of PS channels,the PDF of the channel soft information for BICM-ID is adaptively estimated using the RJMCMC algorithm, and then the soft information is calculated and used to decode iteratively.
The remainder of this paper is organized as follows.In section 2, the dynamic PS channel is modeled, and the parasitic modulation effect on the BPSK signal is analyzed.Section 3 proposes an adaptive P-BICM-ID system over PS channels.Then, numerical examples and analyses under different channel conditions are presented in section 4.Finally,this work is summarized in section 5.
2.Dynamic PS channel modeling and its impact on BPSK signals
2.1.Electron density modeling
During reentry, electron density fluctuates violently and varies in the spatial and temporal domains.The spatiotemporal electron densityNe(z,t)[3] can be described as follows:
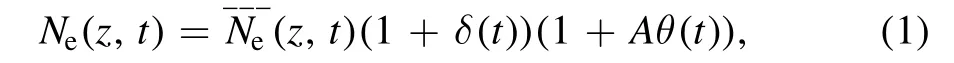
where(z,t)is the average distribution of electron density from the surface of the vehicle outward, θ is the angle of attack(AOA),and A has a typical value of 0.1 per degree[3].δ(t)is the Gaussian jitter [33] with zero mean and standard deviation σmax.Suppose that θ follows a sinusoidal function with amplitude Aθand frequency fθ.In addition,presents large-scale changes in electron density and can be represented by [34]:
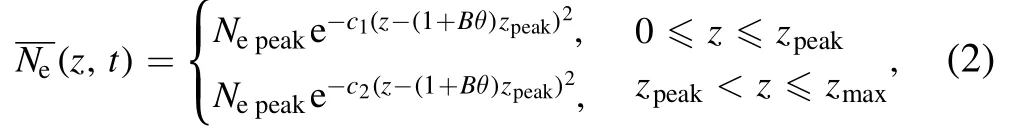
whereNepeakis the peak value of the electron density,zpeakis the position ofNepeak,zmaxis the sheath thickness, c1and c2are parameters,and B is a proportion coefficient with a typical value of 1/14 per degree [35].The typical values ofNe(z,t)are listed in table 1.
In our spatiotemporal electron density model, the largescale change of electron density by flight speed and height,mesoscale change by the angle of attack, and small-scale disturbance are considered.Therefore, the model is suitable for all deep fading, non-stationary, highly dynamic PS channels.Reference [36] also constructs a simple model, which only considers the large-scale and small-scale factors.Our model is more reasonable than this model.What is more,[37]derived the outage probability of NC-MFSK(non-coherent M-ary frequency shift keying)modulation based on our channel model.
2.2.Time-varying plasma sheath channel
To ensure the accuracy and efficiency of calculation,a layered PS model is used to approximate the real continuous model.The PS is modeled as M neighboring uniform thin PS slabs with the complex dielectric constant ε(zm, t)(m = 1, …, M),as shown in figure 1.The layer thickness is dm= zmax/M.The plasma sheath channel h(t)can be precisely calculated by using the transmission line analogy method [33].
ε(zm, t)can be determined by

wherefp(z m,t)is the plasma frequency of the mth layer,v is the electron collision frequency, ω = 2πfEM, and fEMis the carrier frequency.The propagation constantk(z m,t)can be described as

where μ0is vacuum permeability.
The wave impedances of the mth layer is
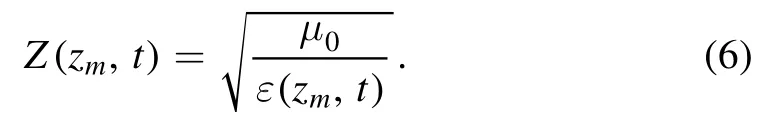
The transmission line matrix can be calculated by

Finally, the overall transmission matrix can be obtained as
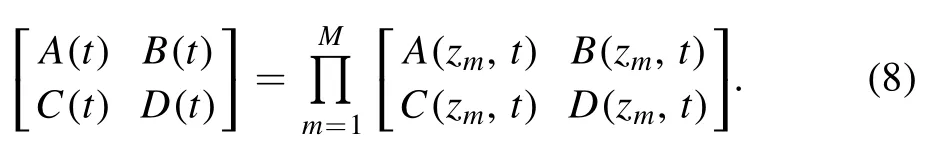
The PS channel h(t)can be calculated by

whereZ(zM+1,t)donates the wave impedance of the(M + 1)th layer andZ(z0,t)presents the wave impedances of the vacuum layer.
2.3.Impact of the dynamic PS channel on BPSK signals
For BPSK modulation with the initial phase±π/2, the signal transmitted in one symbol period is given by
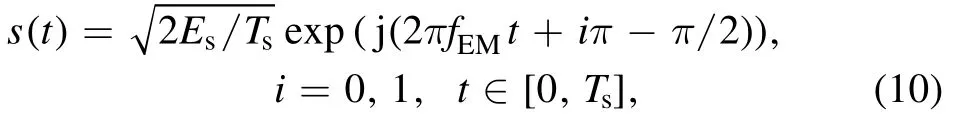
where Esis the symbol energy and Tsis the symbol period.The received signal is expressed as

where n(t)is assumed to be additive white circularly complex Gaussian noise with zero mean and variance σ2.The bit signal-to-noise-ratio (SNR)γbis defined as Es/σ2.
To comprehensively understand the effect of PS channels on BPSK signals, two typical simulations are performed[5, 38].Simulation case 1:Nepeak= 4 × 1018m-3, σmax=0.05, Aθ= 4°, v = 1 GHz, fEM= 32 GHz, and γb= 20 dB;simulation case 2:Nepeak= 1 × 1019m-3, σmax= 0.1, Aθ= 0°, v = 1 GHz, fEM= 32 GHz, and γb= 20 dB.
As shown in figure 2, there are two scattered sets representing bits 0 and 1 in the constellation diagram of the BPSK signals and the constellations rotate dynamically due to the random jitter of the electron density and AOA change,indicating that the dynamics and parasitic modulation effect of PS channels are severe.The statistical characteristics of the signal phases are shown in figure 3.Under case 1, the phase conditional probability density function(CPDF)for bit 0 or 1 presents multipeak features because the change in AOA makes the channel exhibit non-stationary characteristics.Under case 2,since the AOA is equal to 0°,each phase CPDF exhibits one dominating peak.However, two scatter sets representing bits 0 and 1 overlap in constellations whenNepeakincreases to 1 × 1019m-3.This is because the increase inNepeakleads to a more dynamic signal, thereby deteriorating the communication performance.Moreover, unexpected phase shifts occur in the CPDFs, and the phase centers move away from ±π/2 due to the parasitic modulation effect,which brings great difficulties for correct demodulation.
From figures 2 and 3, the PS channel exhibits serious signal attenuation and phase shift effects.Thus,the prior PDF of the received signal is unknown,which makes the traditional soft detector of BICM-ID for PS channels no longer effective.Therefore, the design of a P-BICM-ID system over the PS channel is a great challenge.
3.System model and adaptive scheme
To overcome the above challenge, this work proposes a P-BICM-ID system in which the RJ-MCMC algorithm adaptively estimates soft information.At the receiver, the phase detector is used to calculate and correct the signal phase,and the soft detector is used to adaptively estimate the CPDF of the signal and calculate the soft information.The CPDF of the signal fluctuates randomly with the change in the non-stationary PS channel,and it can be expressed as a mixed Gaussian function.The RJ-MCMC algorithm can be used to adaptively estimate the state parameters of the multi-Gaussian process.The soft information is then calculated based on the estimated PDF of the PSK signal and is used to decode iteratively.
3.1.System model
The proposed adaptive P-BICM-ID system relying on the RJMCMC algorithm is illustrated in figure 4.
The signal to be transmitted is denoted by s = [s1,s2,…,sL], a vector of L BPSK symbols.After the signal travels through the time-varying PS channel, r = [r1, r2, …, rL] is received at the receiver as shown in figure 4.At the transmitter, the information bit stream b is encoded by an LDPC encoder [28] producing the bitstream c, which is then fed to the random bit interleaver π1.The generated stream u is then sent to the unity-rate code (URC)encoder [32], where the produced coded bitstream c′ is interleaved by the interleaver π2, generating the bitstream u′.The URC encoder is used to avoid the BER floor [39].Then, the modulator maps the bits to symbols s.At time instant n, the BPSK signal sntravels through PS channel hn, and the received signal rnis obtained by the receiver.
At the receiver, to achieve better joint demodulation and decoding performance, a phase detector, soft detector, URC decoder, and belief propagation (BP)decoder are employed,as shown in figure 4.The phase detector is used to accurately calculate and correct the phase φ of the received signal r.The URC decoder processes the logarithmic-likelihood ratios(LLRs)L(u′)produced by the soft detector, deinterleaved by π2,the generated L(c′)is passed to the iterative URC and BP decoders, and the a posteriori LLRs Lch,o(c)is computed.Iterative detection is conducted by exchanging extrinsic information between the outer BP decoder and the inner URC decoder.Finally, the estimated bitstreambˆis judged and output.
For LDPC codes, the protograph LDPC codes retain the advantages (approximate to the capacity limit)of traditional LDPC codes and have the advantage of simple structures.In this study, we adopt the promising protograph LDPC code family from the 3GPP TS 38.212 protocol [40], which has a low decoding threshold and a minimum distance that grows linearly with increasing block-length.The code rate Rc=L/N, where L is the information bit number per codeword of length N.The transmitted SNR is defined as γ = γb+ 10log10(Rc).
3.2.Phase detector
Owing to the serious parasitic modulation effect, unexpectedly high phase shifts occur in CPDFs, which brings great difficulties for correct demodulation.To demodulate the information correctly,the signal phase is first amended by the phase detector before estimating the phase CPDFs.
Two problems must be solved when calculating the signal phase.As shown in figure 2, there are obviously twophase clusters corresponding to bits 0 and 1, but the corresponding relationship cannot be determined.In addition,under the effect of parasitic modulation the position of the phase CPDF is shifted and the center phases move away from±π/2, as shown in figure 3.The first problem can be solved by inserting a small number of pilot symbols to distinguish the clusters.For the second problem, an appropriate phase correction method should be executed so that the two dominating peaks are close to the two fixed values ±π/2.In this work, ideal timing synchronization and carrier frequency synchronization is assumed.In actual systems, many synchronization methods can be transmitted to ensure timing synchronization and carrier synchronization, such as Zadoffchu pilots with given frame headers [41, 42], and phaselocked loop technologies [43, 44].
The phase correction is performed as follows:
(1)The phase sequence{φn}of r(t)is first calculated.Next,we divide{φn}into two subsets with a boundary 0,and then acquire the mean value of each subset, p0and p1.
(2)A phase shift |p1+ p0|/2 is performed so that the two dominating peak phases are shifted to approximately ±π/2.
(3)Step(1)to Step(2)are repeated tmaxtimes,where tmaxis the maximum iteration number.Finally, the corrected {φn} is divided into two-phase subsets with a boundary 0.
Letχ0andχ1denote bit subsets representing bits 0 and 1,respectively; Φ0and Φ1can denote the corresponding phase subsets.
3.3.Adaptive soft detector based on RJ-MCMC algorithm
Considering that the CPDF of the signal phase randomly fluctuates with the change in the non-stationary PS channel,prior channel information is difficult to achieve at the receiving end.Therefore,the RJ-MCMC algorithm is used to track the phase CPDF.
Since the corrected phase is disturbed around ±π/2 under the non-stationary PS channel, it can be regarded as a multistate quasi-stationary stochastic variable.The multistate numbers of the two-phase sequences corresponding to bits 0 and 1 are the same because the two sequences experience the same channel.To describe the multistate statistical characteristics, the two received phase sequences can be characterized by mixed Gaussian processes [45] as follows:
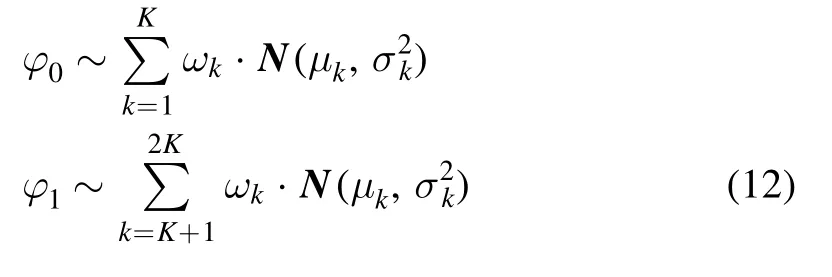
where K is the state number for each mixed Gaussian process,and ωk,μk,andσk2(k = 1,…,2K)are the weight,mean,and variance of the kth sub-distribution, respectively.Furthermore, the RJ-MCMC algorithm [46] is adopted to adaptively distinguish the state number and obtain the distribution parameters.The estimation process is elaborated as follows.
A two-dimensional sequence (φn, zn)is adopted to represent the multistate time-varying process of the phase sequence φnthrough the PS channel, where zn∈{1, …, 2K}indicates the sequence of the corresponding hidden states.
With respect to the RJ-MCMC algorithm,the parameters to be searched areλ=(μ,σ,z,ω),whereμ= (μ),σ = (σk), and ω = (ωk).Their prior distributions are set as follows:
(1)The state number K follows a Poisson distribution with[1, 2..., Kmax], where Kmaxis the largest acceptable value.The initial value K is set as 1.
(2)The weight vector ω obeys the Dirichlet distribution:ω ~D(δ1,δ2,...,δ2K),with the initial valueofδ1,δ2,...,δ2Kequal to1.
(3)μk~N(ξ,κ-1)andσ2k~G(α,β),where the parametersβ~G(α,β),α = 2,κ=∊-2,ξ= φmin+∊/2,g = 0.2,h = 10/∊2,∊= φmax- φmin, φmax= max{φn}, φmin=min{φn}.G(·)denotes the Gamma distribution.
The complete joint PDF, as the distribution of interest[47],is described as
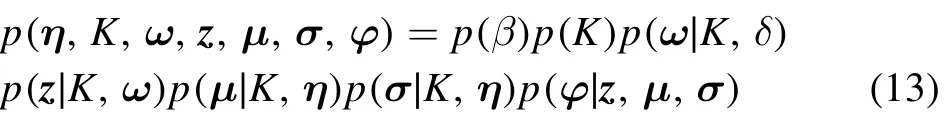
whereη= (α,β,ξ,κ).The parameter spacex=(η,K,ω,z,μ,σ,φ)containing all distribution parameters at iteration N is updated to a new parameter space, i.e.x′ = (η′ ,K′ ,ω′ ,z′ ,μ′ ,σ′ ,φ′)at iteration N + 1.Each iteration from x to x′is categorized in five consecutive moves as follows:
(1)Updateω:

where is the number of states k during iteration N.
(2)Update (μ,σ):

(3)Update z:
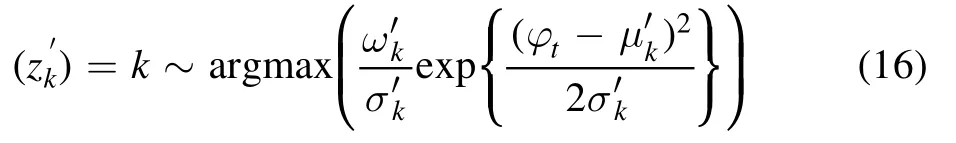
(4)Update β:

(5)Split or combine states.
For the combined states,two channel states are randomly chosen and combined into a new one.Correspondingly, the hidden states are also combined.Conversely, for the split step, a randomly selected state is separated into two.The choice between the split and combine steps depends on the probability dkwhich is a random number following a uniform distribution over (0, 1).
Figure 5 compares the statistical curves and mixed Gaussian curves of the corrected phase CPDFs under two typical cases, where the Gaussian fitting results obtained by the RJ-MCMC algorithm are in red dashed lines and the statistical results are in black solid lines.The two dominating phases corresponding to bits 1 and 0 are shifted to near±π/2,and the PDF shapes exhibit quasi-symmetric characteristics,which also proves the high calculation accuracy of the phase detector.The six-state Gaussian distribution(2K = 6)fits the phase PDF in case 1 and the two-state Gaussian distribution(2K = 2)fits the phase PDF in case 2 by our algorithm.Observe that the mixed Gaussian curves can fit the phase CPDFs well in the two cases,meaning that the phase CPDFs fitted by the RJ-MCMC algorithm can be used in BICM-ID systems.Additionally, notice that the mixed Gaussian curves have some fitting discrepancies near the extreme point of the curves in figure 5(a).The one reason for the fitting discrepancy is the presence of noise, and another reason is thatthe fitted Gaussian state number is small.The more the number of states, the better the fitting effect, but the higher the computational complexity.However,only the intersection of two-phase PDF curves will affect communication performance, so the fitting discrepancy near the extreme point of the curves does not affect the method performance.The larger the intersection area,the worse the performance.Therefore, the fitting result of the curve edges determines the accuracy of the method.Our fitting method can guarantee this with a small state number.
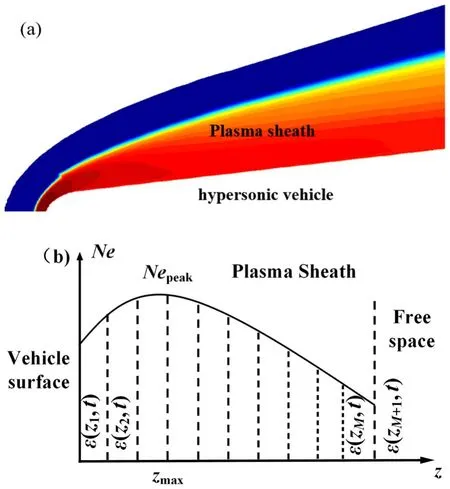
Figure 1.(a)Plasma sheath and(b)layered model of plasma sheath.
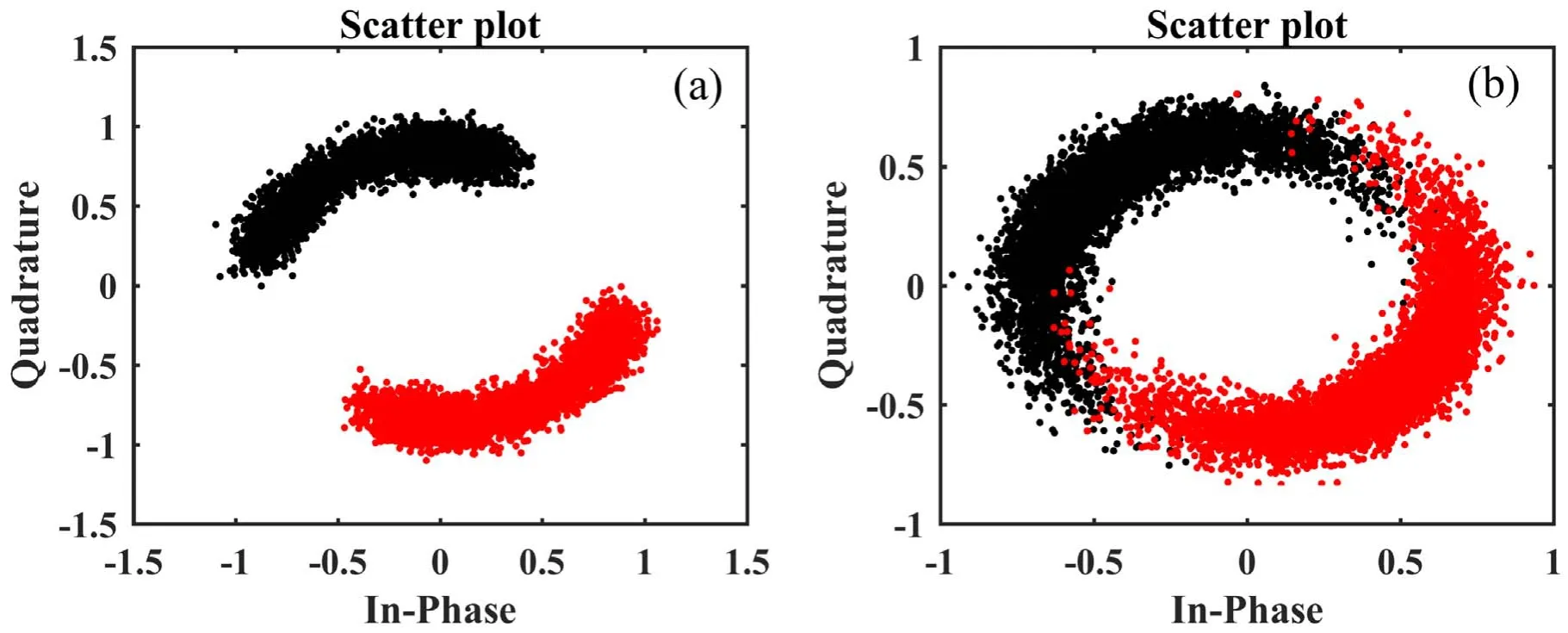
Figure 2.Received signals under (a)case 1 and (b)case 2.
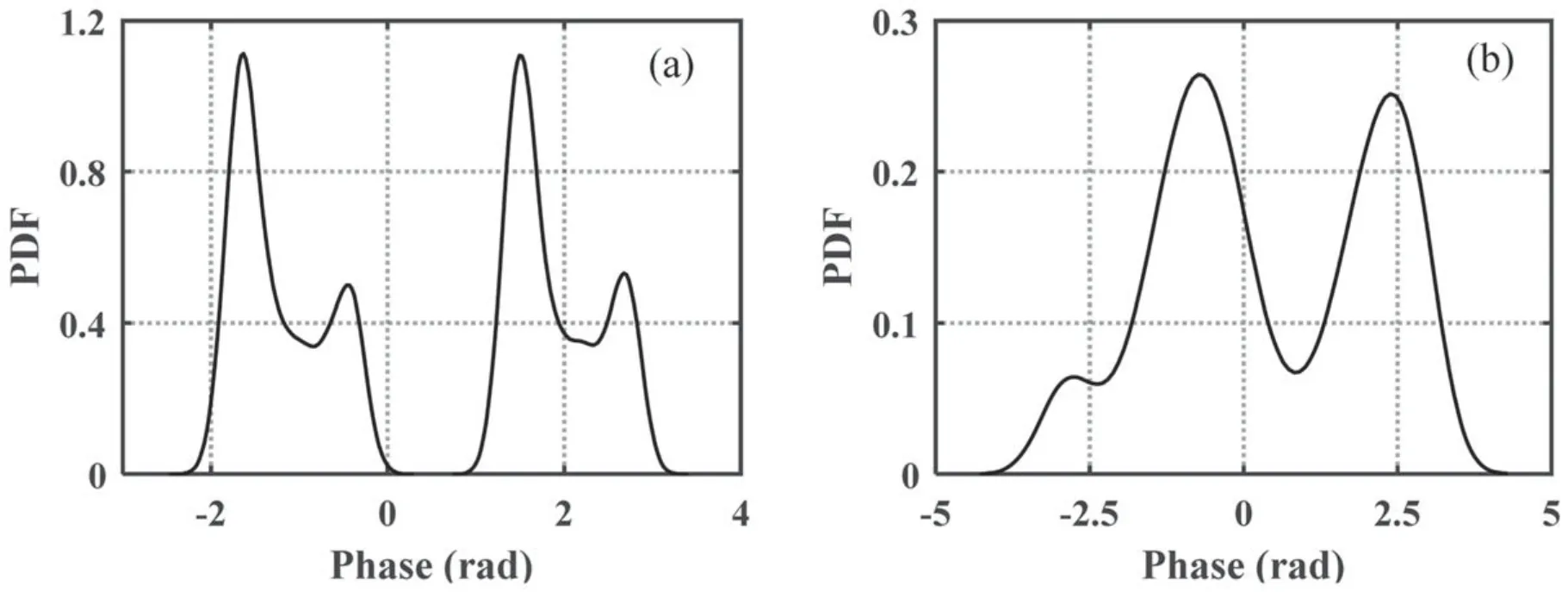
Figure 3.Phase CPDFs under (a)case 1 and (b)case 2.
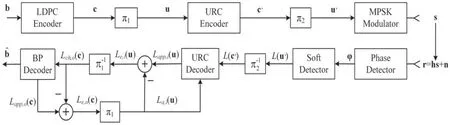
Figure 4.Adaptive P-BICM-ID model over plasma sheath channels.

Figure 5.Results of the statistical model and mixed Gaussian model after phase correction in (a)case 1 and (b)case 2.(Statistical curve displayed in black solid lines and mixed Gaussian curve displayed in red dashed lines.)

Figure 6.BER comparison of our adaptive P-BICM-ID system with those of [23] and [24] under condition 1.

Table 2.States parameters of the mixed Gaussian distributions for case 1.

Table 3.States parameters of the mixed Gaussian distributions for case 2.
Considering the two signal phase sequences corresponding to bits 0 and 1 experience the same PS channel, the multistate numbers of the two sequences are the same and can be determined after the total state number 2K is adaptively estimated by RJ-MCMC algorithm.All state parameters of the mixed Gaussian distribution on two typical cases are listed in tables 2 and 3.It can be seen that the state number for each mixed Gaussian process is 3 for case 1, and the one is 1 for case 2.
After all space parameters are achieved by the RJMCMC, the phase CPDFs for bits 0 and 1,fφ∣χ0(φ∣χ0)andfφ∣χ1(φ∣χ1),can be written as
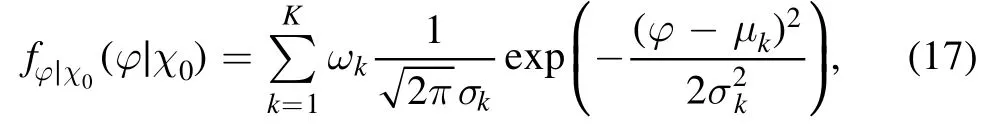
and
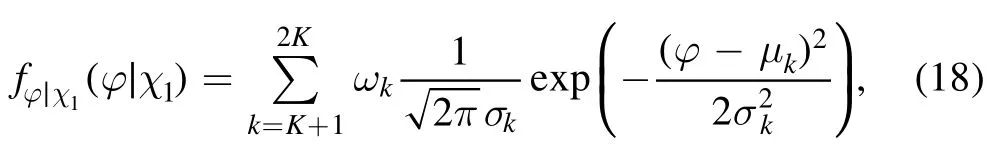
respectively.
At the receiving end, the soft decoder produces the soft phase information for the coded bitstream u′, which is denoted by the LLRL(un′)for the nth bit.Owing to the agreeable Gaussian fitting results, the output of the soft decoder for the nth bit,L(un′),can be represented as

3.4.Iterative URC-BP-decoder
To improve the system performance, a URC detector and a BP decoder with an iterative feedback loop are employed.The key problem lies in designing the interfaces from the soft detector and BP decoder to the URC decoder input port.
For the non-stationary channel, LM( ′un), as the output of the soft decoder, is given by
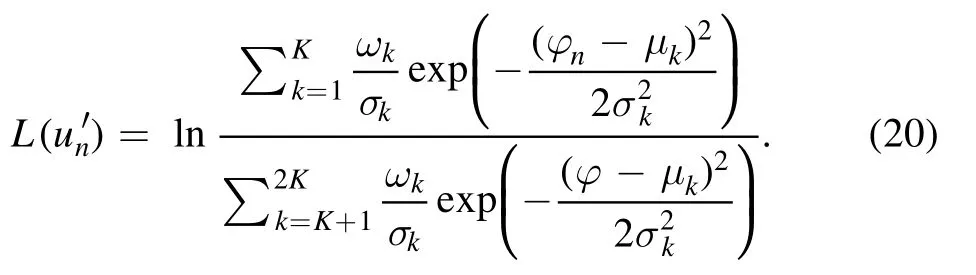
The a posteriori probability P(un|φn)may be computed using thea prioriinformation L(un′)and the informationLa,i(un)gleaned from the outer decoder, which is defined as
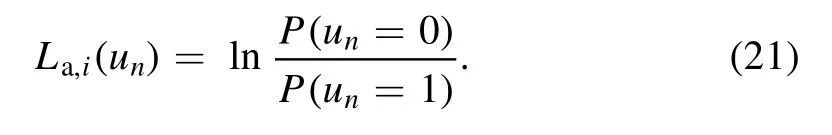
Explicitly, according to Bayes’ rule, we have
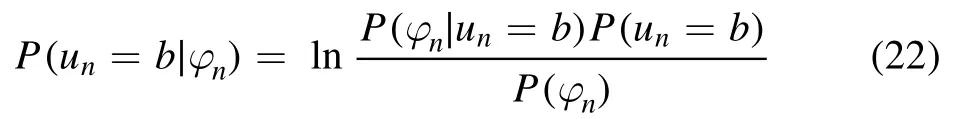
for b∈{0,1}.Based on equations(20)-(22),the URC decoder generates the extrinsic soft information
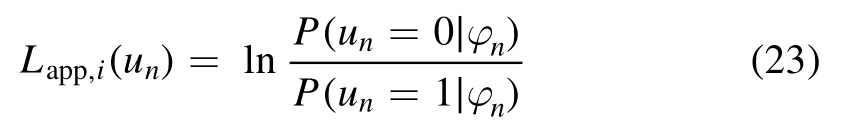
being passed back into the BP decoder.Then, the iterative decoding is performed.
Generally, compared with the traditional BICM-ID system, the program running time of our proposed adaptive system increases by 11%.However, the highly dynamic and non-stationary characteristics and parasitic modulation effects of the PS channel make the traditional BICM-ID system no longer effective.Our solution can use a small computational cost to solve these problems, and the simulations will be introduced in section 4.
4.Simulation results and discussion
This section describes examples of several simulations that were performed to validate the high performance of the new P-BICM-ID system for joint demodulation and decoding under the PS channel.The proposed scheme was compared with the existing methods in terms of BERs under different SNRs.The effects of PS channel parameters and protographs with different code rates and information bit numbers on the new system were also investigated.The simulations prove the superiority of the new method over the other two methods.The proposed adaptive P-BICM-ID system exhibits better performance and has high robustness and adaptability to the highly dynamic PS channel.The plasma sheath parameters in our simulations are described in section 2.Protographs with Rc= {1/2,2/3,3/4,5/6}and L = {528,1056,2112,4224}bits are considered.In addition,we denote the inner and outer iteration numbers by Iiand Io, respectively.
4.1.Method comparison
The adaptive BICM-ID system with different iteration numbers Iois first compared with the methods in[23]and[24]for demodulation and decoding under case 1, as shown in figure 6.For the protograph code, Rc= 1/2, L = 528, and Ii= 10.The performance of the methods in [23] and [24]under case 1 is relatively similar but greatly inferior to that of our adaptive P-BICM-ID system.The adaptive P-BICM-ID system has the best performance with a steep-waterfall region since corrected signal phase CPDFs are used to estimate the soft information and the joint optimization of the LDPC iterative soft decoding and P-BICM-ID system brings both high coding gain and excellent error performance.The performance of the adaptive new system improves as Ioincreases and increases by more than 11 dB at BER = 10-6compared to those of the other two methods.In addition, when Ii=10 and Io=10,the system performance is already very good,and the performance improvement space is limited.Therefore,both Iiand Iocan be chosen as 10 in the analysis below.
Furthermore, we analyze the superiority of the adaptive P-BICM-ID system accurately.It is compared with the methods in[23] and[24]with LDPC codes under case 1 and case 2, as shown in figure 7.The proposed system has a greater than 5 dB improvement over the methods with LDPC codes in [23] and [24] at BER = 10-6under case 1 in figure 7(a).As seen in figure 7(b), the proposed system can reach a BER of 10-6at 22 dB.However, for the other two systems,performance floors appear around BER=10-3as γbincreases.AsNepeakand σmaxincrease, the plasma sheath channel worsens, and the phase jitter becomes stronger.As a result,the schemes with LDPC codes in[23]and[24]cannot cope with this channel situation.From the scheme comparisons, the superiority of the adaptive P-BICM-ID system is proven.
4.2.Robustness analysis
Figures 8 and 9 depict the BER curves of the proposed method under the influence ofNepeakand σmaxor Aθ, where Rc= 1/2 and L = 4224.From the figures, the larger Aθ,σmax,andNepeakare,the stronger the channel non-stationarity,and the worse the system performance.In telemetry communication, 10-6is generally set to be a BER threshold to judge whether there is reliable communication.WhenNepeak=1 × 1018m-3,the BERs for different σmaxor Aθare less than 10-6at γb≥4.5 dB, and the BER curves almost overlap.This means that at a lowNepeak,the impact of σmaxor Aθis trivial.However,whenNepeak=1 × 1019m-3,Nepeakis relatively high, the performance worsens, and the impact of σmaxor Aθis obvious.Therefore, to achieve a BER below 10-6, a larger γbis required.The required γbvalues are 8.2 and 11.6 dB when σmax= 0.05 and 0.1, respectively, as shown in figure 8.The required γbvalues are 8.2 dB,11.0 dB,and 20.9 dB at Aθ= 0°,2°,and 4°,respectively, as shown in figure 9.In general, with increasing σmax, Aθ, andNepeak,the system performance decreases.However, although Aθ, σmax,andNepeakreach 4°, 0.1, and 1 × 1019m-3, respectively, the γbrequired to meet BER = 10-6is still within the acceptable range.Thus, the new scheme is considerably robust to the effects of changes in the PS channel on the performance of demodulation and decoding.
Take the RAM-C reentry flight test [48] as an example.When the reentry flight altitude h = 71 km,Nepeak= 1 × 1017m-3, and Aθ≤4°; when h = 47 km,Nepeak= 1 × 1018m-3, and Aθ≤ 4°; when h = 30 km,Nepeakreaches a maximum of 1 × 1019m-3, and Aθ≤ 4°.The existing communication scheme adopts S- or X- band communication, and the RAM-C vehicle is almost in radio blackout during the flight from 71 km to 30 km [21].However,if the proposed adaptive P-BICM-ID system is adopted,reliable communication during the whole reentry can be ensured when γb≥ 21 dB; reliable communication from 71 km to 47 km can be ensured when γb≥ 4 dB.Therefore,the new system can greatly alleviate radio blackouts.
4.3.Impact of protographs with different Rc and L
Furthermore, we analyze the impact of Rcand L on the decoding performance of the proposed scheme.Figure 10 illustrates the BER variation with γbatNepeak=1 × 1018m-3, and figure 11 depicts the BER variation withNepeakat γb= 8 dB,where protographs with different Rcand L are used; σmax= 0.1 and Aθ= 0°.The BERs decrease significantly with increasing γband increase rapidly with increasingNepeak.This is because with a decrease in γbor an increase inNepeak,the relative intensity of the received signal decreases, which consequently increases the BER rapidly.Moreover, with decreasing Rcor increasing L, considerable code gain occurs and brings a significant reduction in the BER.When a protograph with Rc= 5/6 and L = 528 switches to a protograph with Rc= 1/2 and L = 4224,the γbrequired to reduce the BER to 10-5is lowered from 7.8 dB to 4.3 dB, and theNepeaktolerance limit increases to 8.4 × 1018m-3from 1 × 1018m-3for the same target.
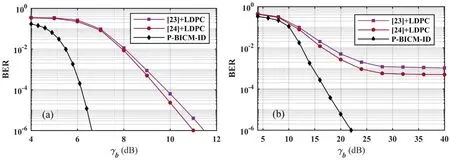
Figure 7.BER curves of our adaptive P-BICM-ID system, [23] with LDPC, and [24] with LDPC under (a)case 1 and (b)case 2.

Figure 8.BER curves with Ne peak = 1×{1018 m-3, 1019 m-3},σmax = 0.05/0.1, Aθ = 0°.

Figure 9.BER curves with Ne peak = 1×{1018 m-3, 1019 m-3}, Aθ= 0°-4°, σmax = 0.05.
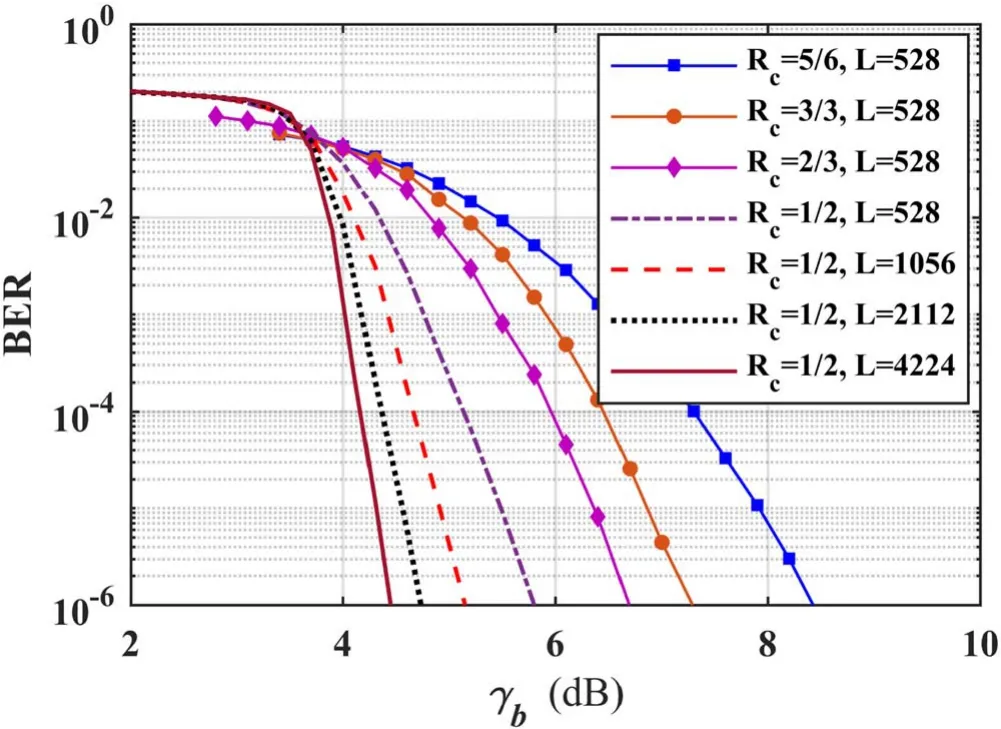
Figure 10.BER versus γb, protographs with different Rc and L,Ne peak = 1 × 1018 m-3, Aθ = 0°, and σmax = 0.1.
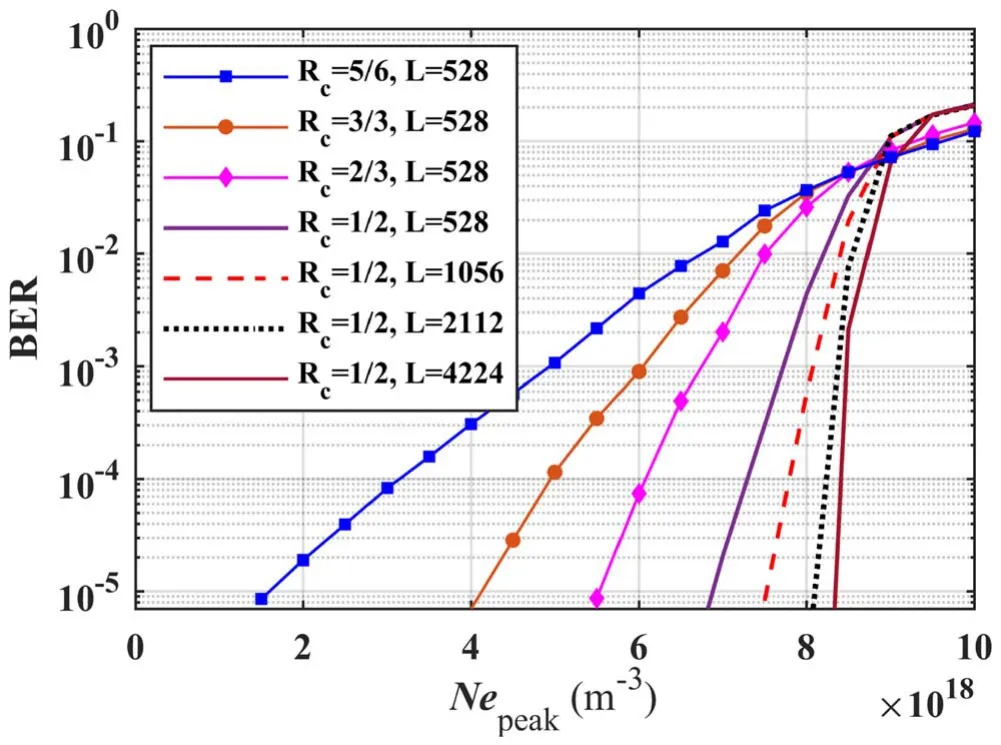
Figure 11.BER versus Ne peak ,protographs with different Rc and L,γb = 8 dB, Aθ = 0°, and σmax = 0.1.
IfNepeakcontinues to increase or γbcontinues to decrease, our adaptive BICM-ID method with a lower Rcor longer L can be adopted to maintain the data link.
5.Conclusions
In this work, we conceive an adaptive P-BICM-ID system based on the RJ-MCMC algorithm for the problem of amplitude fading and phase shift caused by the PS channel.This scheme couples demodulation and decoding by combining protograph LDPC iterative decoding and the BICM-ID framework to make a soft decision over the PS channel, where the phase PDF is adaptively estimated by the RJ-MCMC algorithm and then soft information is calculated.Protograph LDPC codes with high coding gain and low encoding complexity are used to design the coding scheme.Compared to the existing algorithms, our adaptive P-BICMID system has a steep-waterfall performance,obtains a greater than 5 dB performance improvement at 10-6BER, and can cope with a worse plasma sheath environment.Simulation results show that even in the worst case for the plasma sheath during the reentry process, i.e.Nepeak,Aθ, and σmaxreach 1 × 1019m-3, 4°, and 0.1, respectively, the proposed adaptive P-BICM-ID system with an acceptable γbcan ensure reliable communication.In addition, protographs with lower Rcor longer L can be used to further improve the system performance.
Acknowledgments
The authors gratefully acknowledge financial support from National Natural Science Foundation of China (Nos.61871302, 62101406 and 62001340)and the Fundamental Research Funds for the Central Universities (No.JB211311).
ORCID iDs
 Plasma Science and Technology2022年4期
Plasma Science and Technology2022年4期
- Plasma Science and Technology的其它文章
- Quantitative analysis and time-resolved characterization of simulated tokamak exhaust gas by laser-induced breakdown spectroscopy
- Influence of plasma-induced reflected wave variations on microwave transmission characterization of supersonic plasma excited in shock tube
- Quality enhancement and microbial reduction of mung bean (Vigna radiata)sprouts by non-thermal plasma pretreatment of seeds
- In situ quantification of NO synthesis in a warm air glow discharge by WMS-based Mid-IR QCL absorption spectroscopy
- Effects of the electric field at the edge of a substrate to deposit a Ø100 mm uniform diamond film in a 2.45 GHz MPCVD system
- Realizing high efficiency and large-area sterilization by a rotating plasma jet device
