大型渡槽基于反应谱法横向隔震设计方法*
孙家强 陈壮壮 聂利英
(河海大学土木与交通学院 南京 210098)
大型渡槽基于反应谱法横向隔震设计方法*
孙家强 陈壮壮 聂利英
(河海大学土木与交通学院 南京 210098)
为提供简捷的渡槽减隔震设计方法,根据大型渡槽结构特点提出渡槽横向双自由度减隔震模型及基于反应谱法的设计计算公式.其中,以强迫解耦法求振型阻尼比时,由于渡槽上部晃动水体阻尼比与下部减隔震支座等效阻尼比相差较大,故通过对比以强迫解耦法和复模态法求得的振型阻尼比、振型基底剪力,来验证解耦精度.结果表明,第二阶振型解耦精度很好,虽然第一阶振型阻尼比误差较大,但是对于控制设计基底剪力影响很小,因此,得出了强迫解耦法总体上适用于求解减隔震渡槽地震响应的结论.而且,由一阶振型基底剪力贡献分析可知,水体晃动对基底剪力的贡献随着隔震周期取值的增大而显著增大,隔震周期是水体晃动贡献的控制因素.
反应谱法;非经典阻尼;强迫解耦法;水体晃动贡献
0 引 言
我国近20多年来陆续建成各类大型渡槽,有关渡槽减隔震技术的研究,主要采用非线性时程分析方法对减隔震装置的减隔震效果进行研究[1-2].大型渡槽结构形式相对统一,下部结构为实体重力墩或空心重力墩,减隔震时,支座设置成减震耗能装置,因此容易提出力学意义明确且包含水体晃动的减隔震简化模型,在此基础上,若能发展基于反应谱法的实用设计方法,则可为渡槽提供简捷的减隔震设计方法.
在地震作用下,渡槽槽内水体与槽体间的相互作用在顺槽向和横槽向截然不同.当地震激励为顺槽向时,水体与槽壁之间相互作用的摩擦力对顺槽向的震动有减震作用,因此无水情况的空槽模型作为纵向抗震模型既简便又安全[3].当地震激励方向为横槽向时,槽体内水体受槽体两侧壁的约束和支承作用,存在复杂的动力相互作用.由此可知,渡槽的减隔震研究重点在横向,因此,以考虑水体影响的横槽向减隔震设计模型为研究对象.
结构加入减震耗能装置之后,局部阻尼增大,此时隔震结构阻尼矩阵为非经典阻尼矩阵.若以反应谱法为基本分析方法,首先需要对非经典阻尼矩阵进行解耦,以便求得各个振型的阻尼比.复模态法是精确的解耦方法,但必须进行复数运算,且没有直观的物理和工程意义,设计人员难以接受[4].强迫解耦法是一种近似的解耦方法[5],精度与耗能构件阻尼水平[6-7]、分布均匀性[8]、结构自身参数特征[9-11]等有关.渡槽是一种具有独特结构特点的输水结构,上部晃动水体阻尼比一般取值0.5%,下部减隔震支座等效阻尼比最常用取值为15%,上、下两部分相差较大,可能会造成较大的解耦误差,因此,需要对基于反应谱法的渡槽减隔震设计中强迫解耦法在非经典阻尼问题的适用性进行研究.
在强迫解耦法精度研究中,文献[9-10]均以某一典型单体结构为研究背景,研究结果的普适性较差.文献[11]针对规则桥梁的双自由度减隔震模型,以覆盖常用结构参数范围的无量纲参数-即以刚度比、质量比作为观察范围,探讨解耦精度,以提高结果的普适性.
基于此,文中的主要研究内容为:①根据结构特点,提出包含水体晃动作用在内的双自由度渡槽横向减隔震模型,并给出基于反应谱法的计算公式;②参考实际工程的结构参数,归纳概括大型渡槽这一类构造物合理的刚度比、质量比范围,通过与复模态法求得的振型阻尼比、振型基底剪力的对比,论证在渡槽横向减隔震设计中强迫解耦法的适用性;③探讨渡槽横向减隔震中水体的贡献及其控制因素.
1 结构的模型化
1.1 模型提出
目前我国建设的大型渡槽,结构形式较为一致,以南水北调中线工程为例[12],其支撑结构形式多为简支梁式,槽墩为实体重力墩或空心重力墩,槽身横断面多为双槽一联或三槽一联的矩形断面.对于多槽断面,支座位于底肋之下,每个支座的横向水平位移相同,水体晃动由单槽控制,故其模型和设计方法与单槽一致.因此,渡槽横向减隔震模型的研究主要针对单槽矩形断面的简支式渡槽.
渡槽与桥梁结构相似,桥梁在减隔震方面研究成果丰富,所以渡槽横向减隔震模型的研究可参考桥梁双自由度模型的相关研究.对于隔震规则桥梁,桥墩底部固定,上部结构的刚度比隔震支座和桥墩排架的刚度大得多,因此可以将规则桥梁简化成具有两个自由度系统,见图1a).
我国建设的大型渡槽.槽身为混凝土结构,上部设有拉杆,槽身刚度大,槽内有质量巨大水体,在横向地震作用下,水体和槽体两侧壁间存在复杂动力相互作用.模拟槽-水耦合体的经典模型是Housner质量-弹簧模型,在渡槽抗震分析中,选用Housner一阶水体晃动模型通常有足够的精度,文献[13]中矩形槽也采用的是Housner一阶水体晃动模型.
在减隔震研究方面,渡槽结构与储液罐结构类似,储液罐是工程中另一类需要考虑液体晃动的结构.在储液罐减隔震的研究中,储液罐减隔震模型大多采用的也是Housner一阶水体晃动模型.通常将储液罐减隔震模型简化为三自由度系统[14],此三自由度集中质量分别为一阶对流晃动等效质量、罐液耦合等效质量、脉冲等效质量.若壁面刚性大,则可忽略罐壁变形的影响,即可忽略罐液耦合等效质量,此时模型可简化成双自由度系统[15].渡槽槽身刚度大,与双自由度刚性储液罐类似,因此文中采用不考虑壁面振动的Housner一阶水体晃动模型,见图1b).
基于以上的结构特点,文中将晃动水体质量简化一个质点,将固结水体质量与槽体质量作为固结总质量简化成一个质点,进而提出将渡槽横向减隔震模型简化为双自由度系统,见图1c).
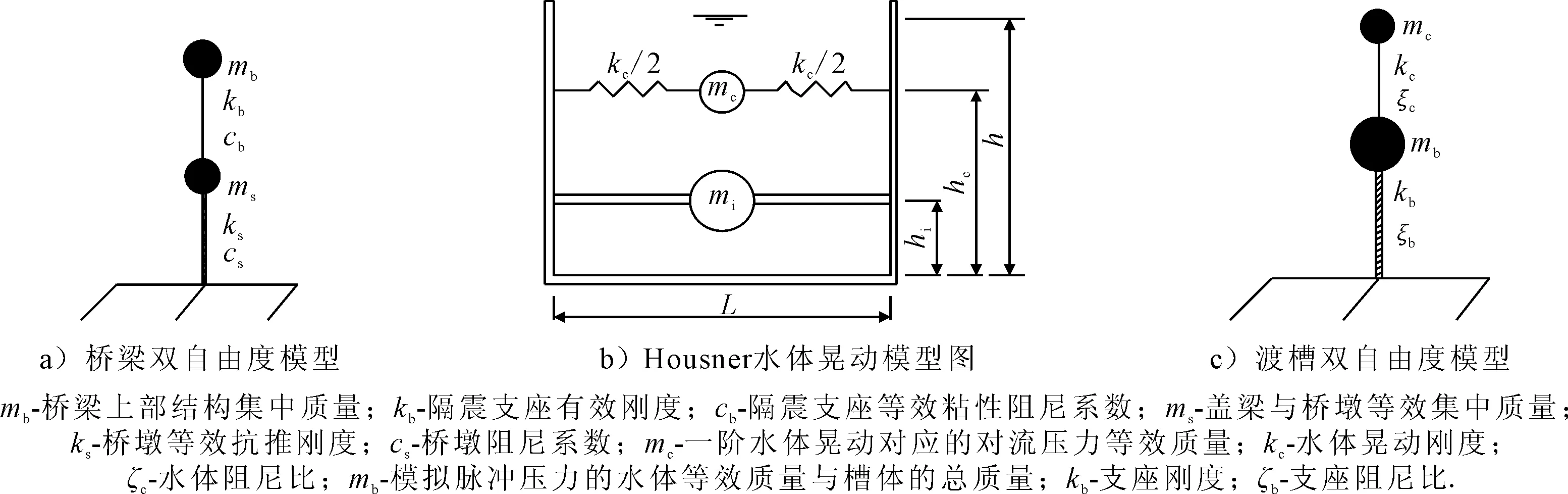
图1 模型分析
1.2 公式推导
渡槽横向双自由度模型中,第一阶振型以水体振动为主;第二阶振型以槽体、支座系统振动为主.渡槽加入减震耗能支座(如铅芯橡胶支座)后,支座阻尼比远远大于上部槽体中晃动水体的阻尼比,此时结构阻尼为非经典阻尼,即阻尼矩阵不再满足振型正交性,从而导致结构振型之间耦合.若以反应谱法求解,则需要对此非经典阻尼矩阵进行解耦,以便分别得到两个振型各自的阻尼比.
渡槽双自由度模型与规则桥梁双自由度模型形式相同,因此,通过强迫解耦法和复模态法求解振型频率、阻尼比详细过程同文献[10],文中以强迫解耦法为例,给出渡槽双自由度模型中控制方程以及振型阻尼比等关键参数的表达式.
(1)
式中:
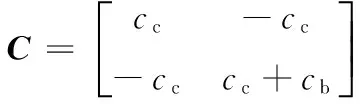
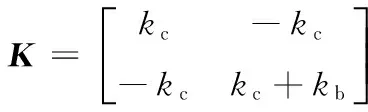
式中:mc,mb为Housner模型中一阶水体晃动质量和固结水体与单跨槽体的总质量;kc,kb为一阶水体晃动的等效刚度和隔震支座的等效刚度;cc,cb为水体阻尼系数和减隔震支座的等效阻尼系数;xc,xb为mc,mb相对地面位移.
根据式(1),在无阻尼自由振动方程下解出第一、第二阶振型自振圆频率与水体自振频率ωc之比α1,α2,见式(2).
(n=1,2)
(2)
式中:γ为质量比,γ=mb/(mb+mc);Rs为刚度比,Rs=kc/kb.
利用强迫解耦法,解得第一、第二阶振型阻尼比表达式,见式(3).
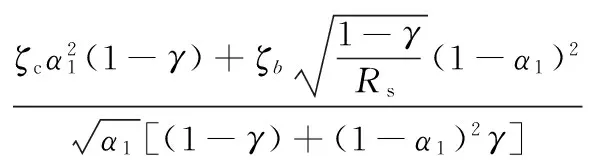
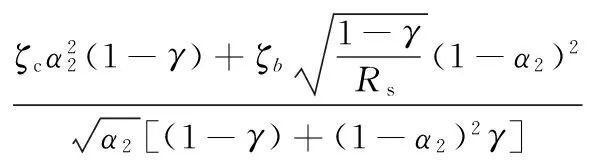
(3)
式中:ζb=ζbeff+ζ0,ζbeff,ζ0,ζc为减隔震支座等效阻尼比、结构自身的体系阻尼比、水体阻尼比.
对于双自由度模型,已知振型阻尼比,以反应谱法为基本求解工具,则地震作用下一阶、二阶振型基底剪力见式(4),其具体推导过程见文献[6].
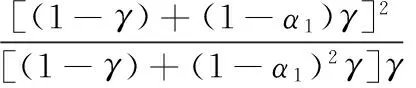
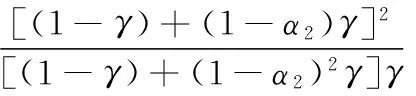
式中:S1,S2为第一、第二阶振型周期对应的反应谱值.
2 强迫解耦法适用性研究
2.1 工程背景以及合理结构参数范围
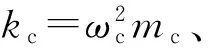
南水北调工程中大型梁式矩形渡槽,其单槽横断面净宽一般均在6 m以上,深宽比0.6~0.8.选取具有代表性的漕河、水北沟、放水河、泲河、洺河渡槽等五个渡槽实际设计尺寸,计算出其质量比、刚度比、隔震前槽体振动周期To、水体的晃动周期Tc,并分析上述参数随着深宽比的变化,参数的变化范围,总结概况一般大型渡槽的结构参数范围,使质量比、刚度比涵盖所有典型结构,以保证结果的普适性.
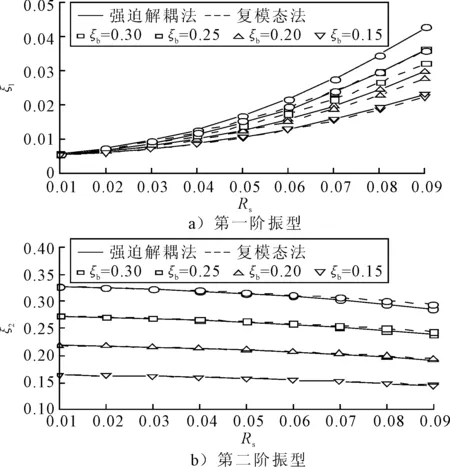
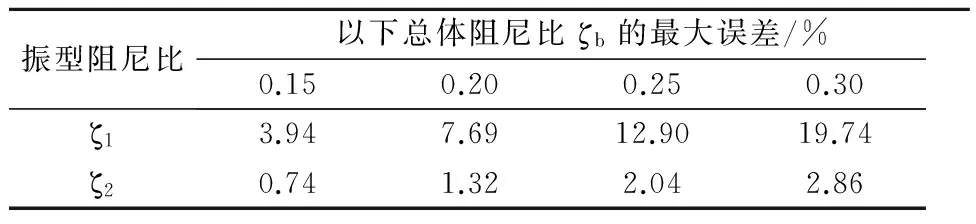
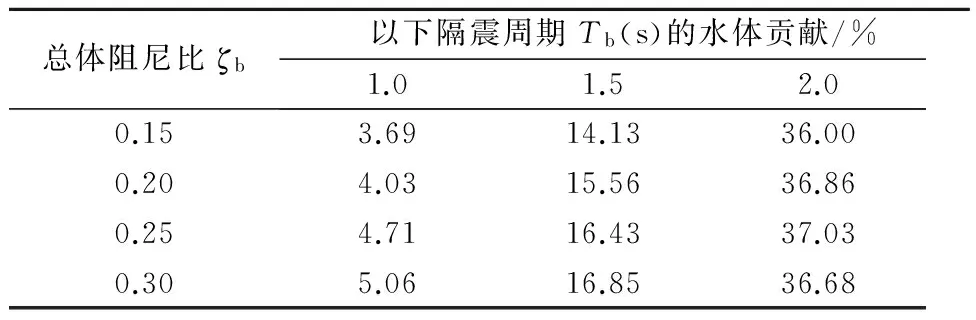
结构参数分析结果为:对于一般槽宽6 m以上的大型渡槽,①质量比分布在0.83~0.87之间;②隔震前槽体振动周期分布范围0.158~0.192 s,一阶水体晃动周期分布范围2.77~3.00 s,因此,隔震周期范围为0.4 s 在减隔震设计中,减隔震支座等效阻尼比ζbeff最常用取值为15%,一般不超过25%,混凝土结构体系阻尼比ζo一般取值为5%,则减隔震支座总体阻尼比ζb=ζbeff+ζ0的范围一般为20%~30%.因此,在后续分析中参数设定如下:支座等效阻尼比选取15%,20%,25%,30%;质量比选取0.83,0.85,0.87,刚度比范围按2.1节选取与质量比对应的参数范围. 对于非经典阻尼,复模态法是精确的解法.因此,通过对比强迫解耦法与复模态法求得的振型阻尼比,验证强迫解耦法的求解精度.由于不同质量比γ=0.83,0.85,0.87及其对应的刚度比范围下得到的振型阻尼比规律类似,所以,文中仅以γ=0.83情况下的结果为例(见图2),对分析结果做详细展示及说明,并对最能反映γ=0.83,0.85,0.87分析结果差异的振型阻尼比最大误差做出说明. 图2 γ=0.83 振型阻尼比 由图2可知,γ=0.83时:①强迫解耦法得到的第一阶振型阻尼比均大于复模态法,第二阶振型阻尼比则均小于复模态法;②减隔震支座总体阻尼比ζb是影响强迫解耦法精度的重要因素,ζb处于小阻尼水平时,两种方法得到的振型阻尼比几乎相同;随着ζb的增大,第一阶振型阻尼比误差随之增大,且误差量大;第二阶振型阻尼比误差虽然也随着ζb的增大而增大,但是误差量总体上很小.两阶振型阻尼比求解误差随ζb不同的具体数据见表3. 表3 振型阻尼比最大误差 注:表中百分比为ABS(强迫解耦法的计算结果/复模态方法的计算结果-1),以此衡量强迫解耦法精度. γ=0.85,0.87与0.83的变化规律类似,其不同点是振型阻尼比误差,支座总体阻尼比ζb取值最大时,误差最大,因此,仅给出ζb=0.30时相关数据.当ζb=0.30时,γ=0.83,0.85,0.87对应的第一阶振型阻尼比的最大误差分别为19.74%,21.84%,24.42%,第二阶振型阻尼比的最大误差分别为2.86%,2.95%,3.04%.由以上数据可知,①强迫解耦法在第一阶振型阻尼比误差的确比较大,且强迫解耦法得到的结果偏大.在必须考虑水体的储液罐隔震研究中,已有对于不同容量的刚性储液罐,液体晃动质量对于基底剪力贡献均超过20%的成果.在渡槽隔震分析中,因水体自身晃动阻尼水平低,若强迫解耦法得到的结果偏大,则存在过渡放大此部分贡献的可能性.②对于渡槽减隔震,第二阶振型为占主要地位的隔震振型,且振型阻尼比误差总体上很小,此结论对以强迫解耦法进行减隔震分析有利. 虽然强迫解耦法在第一阶振型阻尼比误差比较大,但是对于隔震设计,基底剪力才是重要的设计控制参数.因此,分别以强迫解耦法和复模态法得到的振型阻尼比求基底剪力,通过对比判断第一阶振型阻尼比误差对地震响应的影响,从而进一步判断强迫解耦法的适用性.与此同时,观察水体晃动对结构地震响应的贡献. 以反应谱法求解基底剪力,依据文献[16]生成规范反应谱,基本参数为:阻尼比5%、水平加速度峰值为0.2g、Ⅰ类场地、场地系数0.9、场地特征周期0.3 s、抗震重要性系数取1.7,求解过程中依据各自的振型阻尼比以阻尼调整系数修正反应谱谱值.根据式(4)求解第一阶振型、第二阶振型对应的基底剪力V1,V2,并以SRSS振型组合得到基底总剪力.由于在不同质量比γ=0.83,0.85,0.87下分析得到的基底剪力规律类似,因此,仅对γ=0.83的分析结果作图展示,见图3.并对最能反映γ=0.83,0.85,0.87分析结果差异的振型基底剪力最大误差做出说明. 图3 γ=0.83 振型阻尼比 由图3可知,强迫解耦法得到的一阶振型基底剪力均小于复模态法,且随着ζb的增大,强迫解耦法得到的一阶振型基底剪力误差虽然有所放大,但量值比较小,远小于振型阻尼比的误差;二阶振型基底剪力则均大于复模态法,类似振型阻尼比误差分析结果,两种方法在二阶振型基底剪力上吻合度依然非常好.例如ζb=0.30时,强迫解耦法第一阶振型阻尼比的误差达到了19.74%,但该阶振型基底剪力误差却只有5.66%,二阶振型基底剪力误差仅为0.63%,以SRSS振型组合得到的基底总剪力响应误差则为1.82%.各ζb情况下详细数据见表4. γ=0.85,0.87与γ=0.83的变化规律类似, 表4 基底剪力最大误差 其不同点是振型基底剪力误差.当ζb=0.30时,γ=0.83、0.85、0.87对应的一阶振型基底剪力的最大误差分别为5.66%,6.08%,6.86% ,二阶振型基底剪力的最大误差分别为0.63%,0.83%,0.83%. 由表3~4可知,虽然强迫解耦法得到的第一阶振型阻尼比误差大,且解也偏大,但是对一阶振型基底剪力影响却很小;第二阶振型为隔震控制振型,强迫解耦法得到的振型阻尼比、基底剪力与复模态法相比误差极小.由此看出强迫解耦法仍适用于求解减隔震渡槽的地震响应. 由于水体晃动周期长,若减隔震设计中隔震周期设置长,水体晃动贡献相对就大.由2.1节中结构参数分布范围分析可知,隔震周期是确定刚度比的关键参数之一,当隔震周期为短周期时,Tb=1 s,刚度比取值为0.2左右;当隔震周期为中长周期时,Tb=1.5 s,刚度比取值在0.5附近;当隔震周期为长周期时Tb=2.0 s,刚度比的取值为0.9左右.按上述几个刚度比,取图4中强迫解耦法基底剪力的数据(数据位置以虚线表示),分析水体贡献,即一阶振型剪力贡献,见表5. 表5 水体晃动贡献(质量比γ=0.83) 由表5可知,①水体贡献比例受支座等效阻尼比影响很小,这是因为一阶振型基底剪力与基底总剪力受ζb影响而减小的幅度大致相同;②水体贡献随着隔震周期的增大而显著增大,当隔震周期Tb=2.0 s时,水体贡献为36%~37%.这主要是因为当隔震周期取值不断增大时,其不断逼近以水体晃动为主的一阶振型振动周期,因此水体的动力效应随之持续增大;与此同时,隔震周期不断远离以隔震为主的二阶振型振动周期,因此隔震效果随之愈加明显,即SRSS振型组合得到的总剪力逐渐变小,水体晃动贡献所占比例也随之越来越大. 1) 依据大型矩形渡槽结构特征,提出减隔震横向双自由度模型,给出了基于反应谱法的计算公式. 2) 减隔震支座的设置,使动力控制方程中含有的非经典阻尼矩阵,导致结构振型耦合.通过对比强迫解耦法、复模态法求得的第一、第二阶振型阻尼比,发现主要隔震振型(第二阶振型)的阻尼比误差很小,但是第一阶振型的阻尼比误差较大,ζb=0.30时达到了19.74%.随后,以反应谱法为基本分析方法计算基底剪力,结果表明:虽然强迫解耦法求得的第一阶振型阻尼比偏大,且误差大,但是对于基底剪力影响很小,一阶振型基底剪力最大误差仅为5.66%,二阶振型为0.63%,基底总剪力响应最大误差则为1.82%,因此,强迫解耦法适用于求解减隔震渡槽的地震响应. 3) 通过不同隔震周期下水体晃动对基底剪力贡献分析可知,随着隔震周期的增大,水体晃动贡献所占比例也随之增大.在渡槽减隔震设计时,以隔震周期为控制因素,既可以有效控制水体晃动的动力效应,又可以减小结构的地震反应. [1] 王俊,王伟,刘晓平.减隔震装置在特大型渡槽中的应用[J].世界地震工程,2015,31(4):260-263. [2] 季日臣,唐艳,夏修身,等.大型梁式渡槽采用摩擦摆支座的减隔震研究[J].水力发电学报,2013,32(3):213-217. [3] 徐梦华,莫海鸿.流固耦合对大型渡槽纵向地震响应的影响分析[J].武汉理工大学学报,2010,32(11):50-53. [4] ARORA V, SINGH S P, KUNDRA T K. Damped model updating using complex updating parameters[J]. Journal of Sound and Vibration, 2009,320(1):438-451. [5] 俞瑞芳,周锡元.非比例阻尼弹性结构地震反应强迫解耦方法的理论背景和数值检验[J].工业建筑,2005,35(2):52-56. [6] 中华人民共和国建设部.建筑抗震设计规范:GB 50010-2010[S].北京:中国建筑工业出版社,2010. [7] 王昌盛,郑会华,李重稳.非经典阻尼隔震结构近似实空间解耦分析[J].华中科技大学学报(自然科学版),2015,43(1):45-49. [8] 桂国庆,何玉敖.非比例阻尼结构体系近似解耦分析中的误差研究[J].工程力学,1994,11(4):40-45. [9] 刘文锋,李建峰.消能减震结构设计的阻尼比研究[J].世界地震工程,2005,21(2):80-84. [10] 周锡元,俞瑞芳.非比例阻尼线性体系基于规范反应谱的CCQC法[J].工程力学,2006,23(2):10-17. [11] HWANG J S, CHANG K C, TSAI M H. Composite damping ratio of seismically isolated regular bridges [J]. Engineering Structures,1997,19(1):55-62. [12] 顾辉,陈卫国.输水建筑物渡槽工程勘察设计95例[M].北京:中国水利水电出版社,2010. [13] 中华人民共和国国家能源局.水电工程水工建筑物抗震设计规范:NB 35047-2015[S].北京:中国电力出版社,2015. [14] SHRIMALI M K, JANGID R S. Seismic response of liquid storage tanks isolated by sliding bearings[J]. Engineering Structures,2002,24(7):909-921. [15] 孙建刚,蒋峰,王向楠,等.刚性储罐基底隔震的动力反应[J].哈尔滨工程大学学报,2011,32(1):38-43. [16] 中华人民共和国交通运输部.公路工程抗震规范:JTG B02-2013[S].北京:人民交通出版社,2013. Transverse Seismic Isolation Design of Large-scale Aqueduct Based on Response Spectrum Method SUNJiaqiangCHENZhuangzhuangNIELiying (CollegeofCivilandTransportationEngineering,HohaiUniversity,Nanjing210098,China) In order to provide the simple design method of seismic isolation of large-scale aqueduct, transverse two degrees of freedom seismic isolation model of large-scale aqueduct and calculation formula based on response spectrum method are proposed according to the structural characteristics of large-scale aqueduct. When the modal damping ratio of the aqueduct is obtained by the forced decoupling method, there is a big difference between the damping ratio of upper sloshing water and the equivalent damping ratio of the lower isolation bearing. Therefore, decoupling precision can be verified by comparing the modal damping ratio and mode shape base shear obtained by the forced decoupling method and the complex mode method respectively. The results show that the second-order modal decoupling accuracy is very good. Though the error of the first-order modal damping ratio is large, there is little effect on base shear which is the design control response. Therefore, the forced decoupling method can be used to solve the seismic response of the seismic isolation aqueduct. Moreover, based on the contribution analysis of the first-order mode shape base shear, it indicates that the contribution of sloshing water to base shear increases with the increasing of period of seismic isolation, which is the control factor on water sloshing contribution. response spectrum method; non classical damping; forced decoupling method; the contribution of sloshing water TV314 10.3963/j.issn.2095-3844.2017.06.028 2017-10-01 孙家强(1992—):男,硕士生,主要研究领域为桥梁抗震、渡槽减隔震 *国家重点研发计划项目资助(2016YFC0402000、2016YFC0401800)2.2 振型阻尼比分析
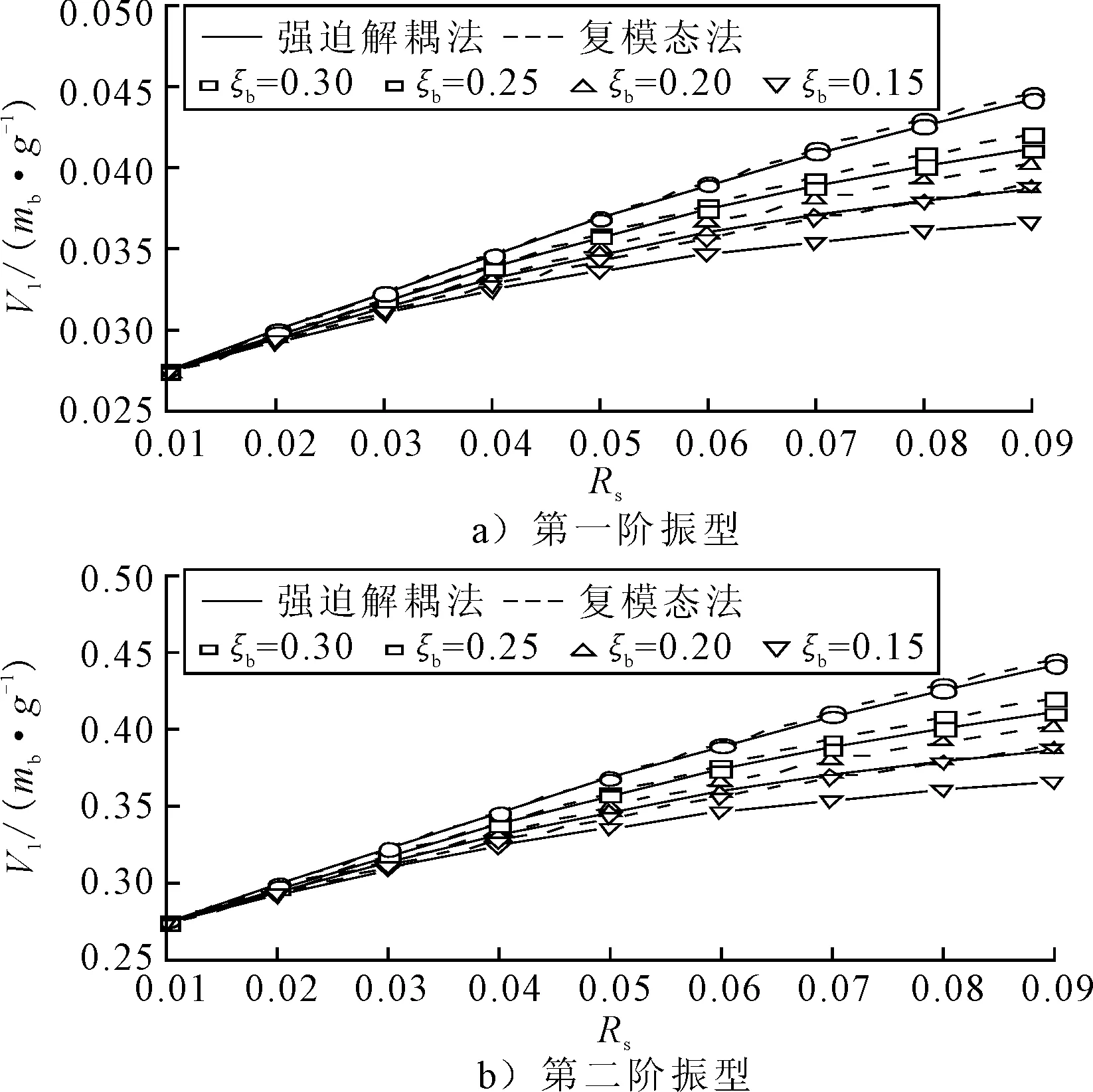
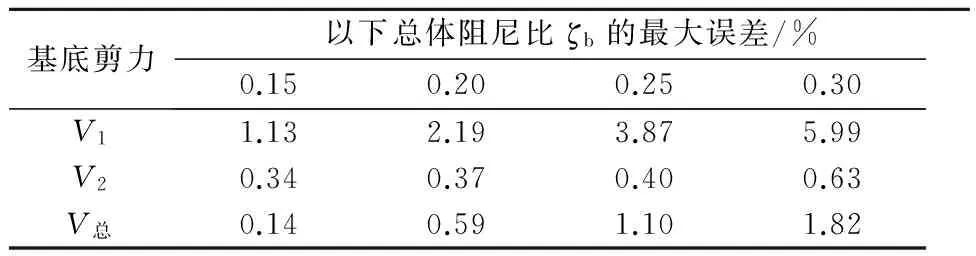
2.3 基底剪力分析
3 结 论
——以东风渠天宫桥渡槽和黎家沟渡槽为例

