车路协同环境下多配送中心DVRP研究*

张 赫 郭文倩 张健松 胡治杰

(大连海事大学交通运输工程学院 大连 116026)

车路协同环境下多配送中心DVRP研究*

张 赫 郭文倩 张健松 胡治杰

(大连海事大学交通运输工程学院 大连 116026)

大数据时代的到来，车路协同技术的应用，使得车辆之间、车辆与交通控制部门、企业之间能够实现实时信息共享，克服传统运输问题中城市配送与实际道路网络脱节的问题，货物能更快更好地到达客户手中，提高企业的配送速度和降低运营成本.路径选择以总费用最小为目标，去掉V/C较大的路段，同时考虑交叉口延误，利用TransCAD与MATLAB结合，求解多配送中心、存在车辆共享和租赁的软时间窗限制的开环VRP问题.结果表明，考虑真实道路网的交通负荷对配送车辆顺畅运行具有重要意义，能够使配送时间减少17.64%，配送费用降低14.85%.

智能交通；车辆路径问题；TransCAD；MATLAB；车路协同；多配送中心

0 引 言

车辆路径问题(vehicle routing problem，VRP)是指在道路线网中，在满足客户需求前提下，找到符合配送车辆载重量要求的线路，使总费用(包括固定成本，运输费用不满足时间窗要求的机会成本和惩罚成本)最少、运输时间最短等目标.通常意义上的静态VRP已经不能适应现代运输的需求,因此，文中在车路协同环境下，配送中心、客户通过交通管理信息的共享，构建配送信息平台，研究动态车辆路径问题(DVRP)，使其既能满足客户的需要，又使企业达到效益最大化.

关于DVRP的研究，Victor等[1]对动态路径问题进行了研究综述.Potvin等[2]针对客户需求动态和行驶时间动态，提出了不同的调度策略.王旭等[3]建立了基于时间轴的DVRP模型，设计了“初始优化+实时优化”两阶段的求解策略，根据动态客户需求局部调整计划路径.张婷等[4]将动态车辆路径问题转化为静态，针对需求量变化、需求点增减、道路中断、车辆故障四种动态情形下的配送线路实时优化问题.李妍峰等[5]提出车辆接受实时交通信息，在关键点更新配送线路.

对于多配送中心车辆路径问题，于滨等[6]提出“先分类，后优化”的思想，将多配送中心问题转化为多个单配送中心VRP问题，然后用改进的蚁群算法进行求解.王万良等[7]对存在多配送中心、车辆共享的软时间窗动态需求VRP问题，建立了两阶段模型，并运用混合3-opt量子进化算法进行求解.刘家利等[8]提出了多配送中心、存在车辆共享和租赁的有时间窗限制的开环VRP问题，引入虚拟配送中心，将多配送中心转化为单配送中心，并通过混合遗传算法求解.

虽然对于多配送中心VRP问题已有大量研究，但大多并没有结合实际路网，考虑在实时交通信息下道路网络对配送车辆的影响.针对目前研究存在的问题，文中考虑了在实时交通网路中，存在配送中心之间车辆共享且能够从其他机构租赁车辆的多配送中心VRP问题，并且考虑车辆不必返回原配送中心，就近回到配送中心，以达到配送中心间运力均衡，总费用最小的目的.

1 车路协同系统

车路协同系统[9](cooperative vehicle infrastructure system，CVIS)主要由无线通信模块、路边协调控制模块以及智能车载设备构成，这与现代物流配送系统的需求不谋而合.现代物流配送系统信息传递是根据客户需求，结合交通管理中心获取服务区域的基本路况、车辆位置、服务地点，计划当前路径，反馈给配送中心及车辆，实现物流配送和道路网络的协调互动，见图1.城市运输调度系统在信息平台的基础上，通过借助GIS、GPS、ITS等技术获取动态信息，使得客户能够在灵活地变更货运需求，配送中心车辆能够灵活地调度，见图2.

图1 现代物流运输信息传递

图2 城市运输调度系统

2 问题描述与模型建立

2.1 问题描述

文中描述的存在车辆共享和实时交通信息的多配送中心动态需求的车辆路径问题描述如下.

假设有M个配送中心，储备同种货物，N个客户，每个配送中心拥有额定载重量为Q的配送车辆Km辆.配送车辆从配送中心出发，完成配送任务后返回使总体费用最小的配送中心.每个客户只能由一辆车为其服务且只能服务一次，客户的需求量不能超过车辆的额定载货量.在一个计划期内，每辆车的工作时间不能超过规定的最大工作时间T，最长运输距离为D，配送车辆在配送中心的装卸时间为wtomk，在客户点的装卸时间为wtnmk，客户n的需求量为qn，其服务时间窗为[ETn，LTn]在服务过程中会有新的客户需求.如果某个配送中心所需的车辆数多于该配送中心目前拥有的车辆数，可以从其临近的配送中心调用车辆.所寻求的目标是在实时交通信息下找出合适的调度方案，满足客户的时间窗要求，并使总的运输成本最小.文中仅考虑送货情况.

2.2 参数说明

Wr为单位车辆的固定成本；Wf为单位时间单位配送车辆的运输成本；tijmk为配送中心m第k辆车从点i到点j的实际运输时间；M为无穷大的惩罚成本；P(t)为未满足时间窗要求，配送车辆所需付出的成本损失(惩罚费用)；Tnmk为配送中心m第k辆车到达客户点n的时刻；qnmk为配送中心m的车辆k运输的客户n的需求量.

决策变量：

xijmk=

ynmk=

2.3 模型建立

1) 预优化模型 在预优化阶段，根据已知客户信息和静态交通信息安排车辆的初始运行线路，若某个配送中心车辆供不应求，可从其他配送中心调用车辆.假设车辆共享是在对客户进行服务之前完成，即对客户服务的时间窗没有影响.

(1)

式中：P(t)为分段函数，函数关系见式(2).

(2)

注：a=100元/h;b=200元/h.

2) 实时优化模型 配送车辆每经过一个关键点(交叉口和客户点)，配送线路会根据实时交通信息和新的客户需求进行更新.此时，预优化阶段的车辆已经服务了部分客户，车辆所载货量也相应减少，在实时交通状况和车辆剩余货量的情况下，将新客户加入到配送线路中，如若现有配送车辆不能满足新客户需求，则需要重新安排.

在实时优化阶段，U为第一阶段未服务客户数和新加入的客户数量，第一阶段车辆的剩余载货量为Qe，第二阶段各配送中心派车Pm.

(3)

s.t.

k∈{1,2,…,Km},m∈{1,2,…,M}

(4)

k∈{1,2,…,Km},m∈{1,2,…,M}

(5)

(6)

(7)

m∈{1,2,…,M}

(8)

n∈{1,2,…,N}，k∈{1,2,…,Km},

m∈{1,2,…,M}

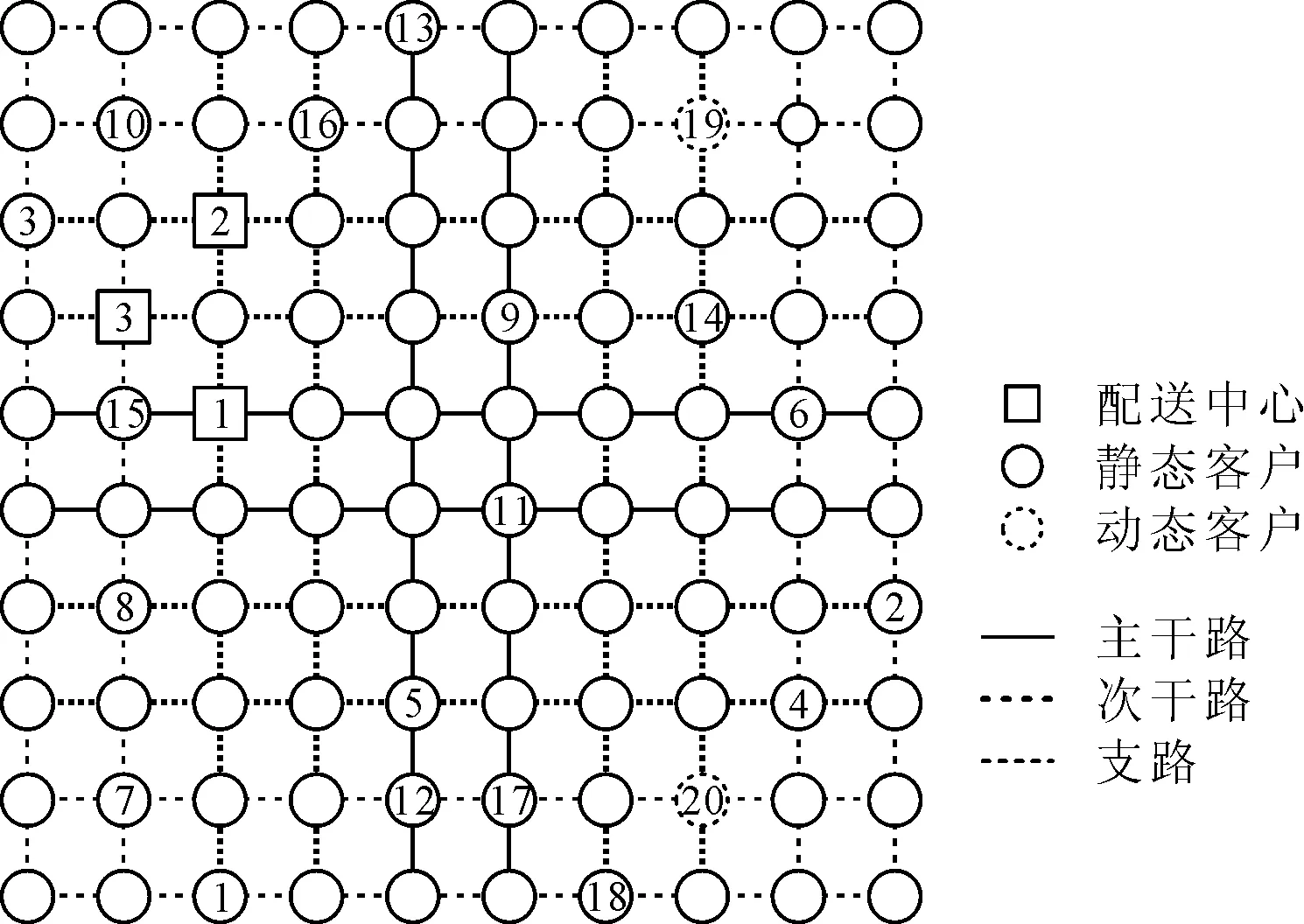
(9)

n,h∈{1,2,…,N}，Tnmk

(10)

k∈{1,2,…,Km},m∈{1,2,…,M}

(11)

xinmk(Tnmk+tinmk+wtnmk-Thmk)≤0,

i∈{1,2,…,M,M+1,…,M+N},

n,h∈{1,2,…,N},

k∈{1,2,…,Km},m∈{1,2,…,M}

(12)

(∀S⊂{1,2,…,N},且2≤|S|≤n-2)(13)

式(3)为目标函数，总费用最小；式(4)保证车辆载重量不超过额定载重量；式(5)保证配送车辆行驶距离不超过车辆单次能够行驶的最大距离；式(6)保证一辆配送车辆最多只能到达客户点一次；式(7)保证每个客户只能被一辆车服务；式(8)保证车辆满载出发；式(9)保证车辆在服务某客户前，剩余载货量能够满足该客户的需求量；式(10)为配送车辆服务完客户后，剩余载货量的变化关系；式(11)保证配送车辆的工作时间不大于最大工作时间；式(12)若两客户被同辆车服务，服务时间要满足先后顺序；式(13)避免子回路.

3 车路协同环境下的多配送中心动态车辆路径问题

3.1 考虑交叉口延误的动态最短路径

在城市道路系统中，交叉口是交通顺畅运行的瓶颈，由于交叉口转向而引起的时间延误可以达到全部行程时间的17%～35%，因此，文中在计算道路网络的最短路径时，考虑了交叉口延误，粗略按路段行程时间的20%计算.

文中用10×10的网格模拟道路网，见图3.该路网中有100个交叉口，180条路段.假设路网中所有路段均是双向，任意两个客户之间有多条路径可以连通，每条路段的实时行程时间由式(14)交通阻抗函数得出[10].由于交通流具有相似性，同时为了避免海量数据计算的复杂性，文中每15 min收集一次交通流数据，并取上一个15 min的数据用于实时计算.

(14)

式中：toijmk为配送中心m第k辆车在自由流条件下，从点i到点j的运输时间dij/v;Cij为点i到点j的路段的通行能力；xij为点i到点j的路段的实际交通量；α，ρ为参数(取α=0.15，ρ=1.00).

图3 道路网及客户点

3.2 车路协同环境下的运行流程

DVRP问题的求解，属于NP-hard问题，很多学者已经对其作出了大量研究，文中利用TransCAD与MATLAB的结合，采用混合遗传算法进行求解，其流程图见图4.

图4 运行流程图

4 实例分析

文中所用10×10的道路网，每条路段的长度为5 km，路网中的主干道、次干道和支路，其自由流情况下的速度分别为50,40和20 km/h，分为对应的自由流状态下的路段行程时间分别为0.1,0.125和0.2 h.文中随机生成18个静态客户，两个动态客户，动态客户19，20分别在10 min，1 h时发出送货请求，客户点、配送中心分布见图5.假定配送车辆的额定载货量为4 t，单次能够行驶的最大距离为100 km，配送中心的工作时间为[0 h,10 h]，客户能够接受的等待时间是在发出送货请求后的两小时之内，且每个客户的送货需求都为1 t.配送过程中每使用一辆车所产生的固定成本为1 000元/辆，单位时间每辆车的配送成本为50元/h.配送中心Ⅰ拥有车辆V1，配送中心Ⅱ拥有车辆V2，V3，配送中心Ⅲ拥有车辆V4，V5.

根据以上数据，图5a)的路线表示初始状态下的配送线路，服务顺序及费用见表1.在运行过程中，根据实时交通流信息，道路V/C大于0.8，认为比较拥堵，在路径选择过程中去掉这些路段，避免加重这些路段的交通压力，导致送货延迟.利用实时交通信息，结合新的客户信息，车路协同环境下的配送路线服务顺序，见图5b).

图5 配送路线图

车辆编号优化前后起始配送中心服务客户顺序返回配送中心服务时间/h费用/元1初始Ⅰ18-17-12-5Ⅰ4.2851851.250优化Ⅰ11-2-4-20Ⅰ3.9471262.9502初始Ⅱ3-10-13-16Ⅱ2.3281142.580优化Ⅱ3-10-16-13Ⅱ2.0331101.6253初始Ⅰ11-2-4Ⅰ4.5571502.825优化Ⅱ5-12-17-18Ⅰ2.7581182.8754初始Ⅲ15-8-7-1Ⅰ2.3121115.575优化Ⅲ15-8-7-1Ⅰ2.3121115.5755初始Ⅲ9-14-6Ⅰ3.2561199.000优化Ⅲ9-14-6-19Ⅱ3.1561157.675初始合计16.7386811.23优化合计13.7865820.70

由表1可知，如果不进行实时线路优化，按照初始线路配送货物时，运输时间长，费用高，并且有六位客户未满足时间窗要求，没有在规定时间内送达.而根据实时交通流信息调整线路，避免了配送车辆进入拥挤路段，加快了运输速度，更易满足客户的时间要求，配送时间减少17.64%，也节省的企业的运输成本，配送费用降低14.54%.

5 结 束 语

针对目前车辆路径问题的研究所存在的缺少与实际路网有效结合，造成了配送车辆在道路网运行过程中无法达到预计效果的问题，同时从物流企业本身的效益出发，能使企业在投入最少的车辆成本的情况下，通过车辆共享实现企业内车辆的有效利用，也可借助租赁的方式实现企业效益的最大化.在车路协同环境下，利用实时的交通流信息，从大数据带来的海量数据着手研究动态车辆路径问题对于现代物流企业的调度管理具有重要的实践价值.

[1] VICTOR P, MICHEL G, CHRISTELLE G. A review of dynamic vehicle routing problems[J]. European Journal of Operational Research,2013,225(1):1-11.

[2] POTVIN J Y, XU Y, BENYAHIA I. Vehicle routing and scheduling with dynamic travel times[J]. Computers &Operations Researvh,2006,33(4):1129-1137.

[3] 王旭,葛显龙,代应.基于两阶段求解算法的动态车辆调度问题研究[J].控制与决策,2012,27(2):175-181.

[4] 张婷,赖平仲,何勤飞，等.基于实时信息的城市配送车辆动态路径优化[J].系统工程,2015,33(7):58-64.

[5] 李妍峰,高自幼,李军.动态网络车辆路径派送问题研究[J].管理科学学报,2014,17(8):1-9.

[6] 于滨,靳鹏欢,杨忠振.两阶段启发式算法求解带时间窗的多中心车辆路径问题[J].系统工程理论与实践,2012,32(8):1793-1800.

[7] 王万良,黄海鹏,赵燕伟，等.基于车辆共享的软时间窗动态需求车辆路径问题[J].计算机集成制造系统,2011,17(5):1056-1063.

[8] 刘家利,马祖军.存在车辆租赁及共享且有时间窗的多配送中心开环VRP[J].系统工程理论与实践,2013,33(3):666-675.

[9] TANIKELLA H, SMITH B L, ZHANG G. Development of a VII-enabled prototype intersection collision warning system[J]. Journal of Computing in Civil Engineering,2007,11:434-440.

[10] 杨忠振,穆雪,朱晓聪.交通流变化下的多配送中心：多需求点配送网络优化模型[J].交通运输工程学报,2015,15(1):101-107.

Research on Multi-depot Dynamic Vehicle Routing Problem Under IntelliDriverSM

ZHANGHeGUOWenqianZHANGJiansongHUZhijie

(TransportationManagementCollege,DalianMaritimeUniversity,Dalian116026,China)

With the advent of big data era, the application of vehicle road technology makes the real-time information sharing between vehicles, traffic control departments and enterprises, which overcomes the problems of urban transportation and the actual road network in traditional transportation problems, makes the goods faster and better, and improves the delivery speed and reduces operating costs. The target of path selection is to minimize the total cost, removing the largerV/Cvalue during path selection. Taking the intersection delay into consideration and combining TransCAD with MATLAB, the open-loop vehicle routing problem (VRP) under multi-depot and soft time Windows restriction based on vehicle sharing and leasing, is solved. The results show that considering the real road network traffic load is significant to keep vehicle running smoothly. The delivery time will reduce by 17.64% and the distribution costs will reduce by 14.85%.

intelligent transportation; vehicle routing problem(VRP); TransCAD; MATLAB; IntelliDriverSM; multi-depot

U491.2

10.3963/j.issn.2095-3844.2017.06.001

2017-10-26

张赫(1971—)：男，博士，副教授，主要研究领域为智能运输系统、交通运输规划与管理、交通控制、智能物流系统

*国家重点研发计划重点专项项目资助(2017YFC0805309)