水介质对船舶轴桨组合振动模态影响*

李小军 朱汉华 许浩然 吴继东 熊 维

(武汉理工大学能源与动力工程学院1) 武汉 4300630) (武昌船舶重工集团有限公司2) 武汉 430060)

水介质对船舶轴桨组合振动模态影响*

李小军1)朱汉华1)许浩然1)吴继东2)熊 维2)

(武汉理工大学能源与动力工程学院1)武汉 4300630) (武昌船舶重工集团有限公司2)武汉 430060)

为了分析水介质对船舶轴桨组合结构振动模态的影响，基于流固耦合动力学方程，在ANSYS Workbench平台计算了某船舶轴桨组合结构在水介质中的振动模态.通过单向流固耦合计算流场预应力对结构振动模态的影响；通过在Workbench中耦合APDL命令流，计算了流场预应力下轴桨组合结构在空气中和水介质中的模态分布.结果表明，流场预应力略微提高结构刚度，其固有频率略微提高；附水质量明显降低结构固有振动频率，但是干湿模态振型顺序相同；水介质阻尼降低固有振动幅值.

船舶轴系；螺旋桨；振动；水介质；流固耦合

0 引 言

船舶在航行中，由于螺旋桨在水介质中所受推力和转矩较大，传递给轴系后，会影响轴桨组合结构振动特性.同时螺旋桨运转中受到附加水质量、阻尼力等作用，也会影响轴桨组合的振动特性[1]，因此，研究水介质对于船舶螺旋桨和轴系组合结构振动特性的影响是有必要的.

针对螺旋桨附连水效应，由于水下试验比较繁琐，成本较高，因此一般采用附连水系数来估计，周春良[2]取附连水系数1.3和1.25，分析了附连水质量对轴系固有振动特性影响，该方法虽然简单，但是精度不高.随着边界元和有限元理论的出现及计算机的迅猛发展，使得流固耦合数值方法在旋转机械领域得到了较快发展[3].Mauro等[4]通过在椭圆坐标系下求解流体运动的边值问题，计算附加质量矩阵，对部分浸没的悬臂板的固有频率进行流固耦合分析.娄本强[5]在无限域流场中对螺旋桨湿模态分析，并进行实验验证；刘强等[6]采用结构有限元耦合流体边界元的虚拟质量法，运用MSC.NASTRAN 计算了螺旋桨在空气中和水中的固有频率和振型，但是这些仅仅考虑了螺旋桨在水中的模态，未考虑水介质对轴桨组合结构振动影响.施卫东等[7]运用Workbench和APDL命令流耦合的方法，结合流固耦合方法，计算了大型潜水轴流泵(包括叶轮和转轴)在水压力作为预应力情况下，以及水介质中的模态分布.

文中基于流固耦合动力学方程，在ANSYS Workbench平台，计入水介质、附水质量,以及水介质阻尼的影响，研究轴桨组合结构的振动模态.利用CFX软件计算螺旋桨在流场介质中的压力载荷，并通过流固耦合面施加到结构场中桨叶表面，对轴桨组合结构进行有预应力的模态分析；通过APDL命令流的方式，采用结构模态分析的非对称法，对轴桨组合结构进行湿模态分析，比较了干湿模态固有频率和振型的变化规律.

1 计算方法

1.1 空气中动力学方程

空气中离散的结构动力学方程为

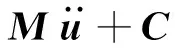
(1)

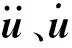
当求解空气中模态时，C=0，F(t)=0，即系统在做无阻尼的自由振动，方程可简化为

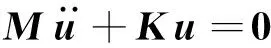
(2)

1.2 水介质中动力学方程

考虑流体压力作用时，结构动力学方程需要与流体Navier-Stokes方程同时进行考虑，此时系统的自由振动方程为

(3)

式中：Kfs为流体作用在结构上的刚度矩阵；p为流体声学压力.

考虑水介质的附加质量和阻尼作用时，假设流体为无旋、无粘、均匀的可压缩流体，ANSYS结构动力学模态分析中的非对称方法，将流体压力作为流场中的基本未知量来求解结构的水下模态.其三维波动方程为

目前有关天线近场区场的综合工作较少。文献[8]提出了利用时间反演控制近场区电磁场的方法，然而整个系统非常昂贵，而且处理数据的过程相对耗时。

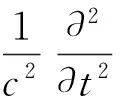
(4)

式中：c为流体中声速.

波动方程离散化得

(5)

联立式(1)得流固耦合动力学方程为：

(6)

2 模型的建立

2.1 模型基本参数及三维模型建立

文中以西江干线某船的轴系和螺旋桨作为研究对象，螺旋桨为MAU型等螺距桨，轴系包括一根艉轴和三根中间轴，含前后尾轴承和三个中间轴轴承.轴桨材料性能参数如下：密度7 850 kg/m3，弹性模量E=206 GPa，泊松比μ=0.3.

通过已知的螺旋桨叶二维型值点坐标，计算出螺旋桨的三维型值点，将其转化为pts格式导入Pro/E软件中，连成曲线，建立空间曲面，再通过边界混合命令曲面混合生成螺旋桨叶实体，最后通过圆周阵列将其与轴毂合成一体，建立螺旋桨的三维模型，最后与轴系进行合并.螺旋桨主要参数见表1，轴系主要参数见表2，轴桨组合模型见图1.

表1 螺旋桨主要参数

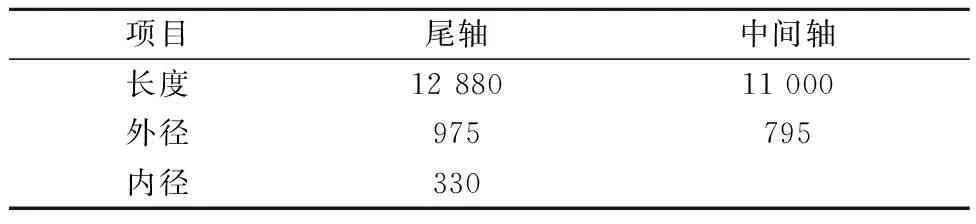
表2 轴系主要尺寸参数 mm

图1 轴桨组合模型

2.2 流体域的建立及边界条件的设置

流体域采用分区网格划分，计算域由固定域和旋转域组成，固定域为外部大圆柱体(直径5D，长12D)，采用结构化六面体网格划分，旋转域为内部小圆柱体(直径2D、长1.5D)，两个区采用CFX的GGI方式连接.对螺旋桨叶梢和叶根处进行加密，在螺旋桨桨叶外设置三层边界层.最终生成四面体网格数为433 563个，六面体网格数为321 245个.螺旋桨表面和流场域网格见图2.

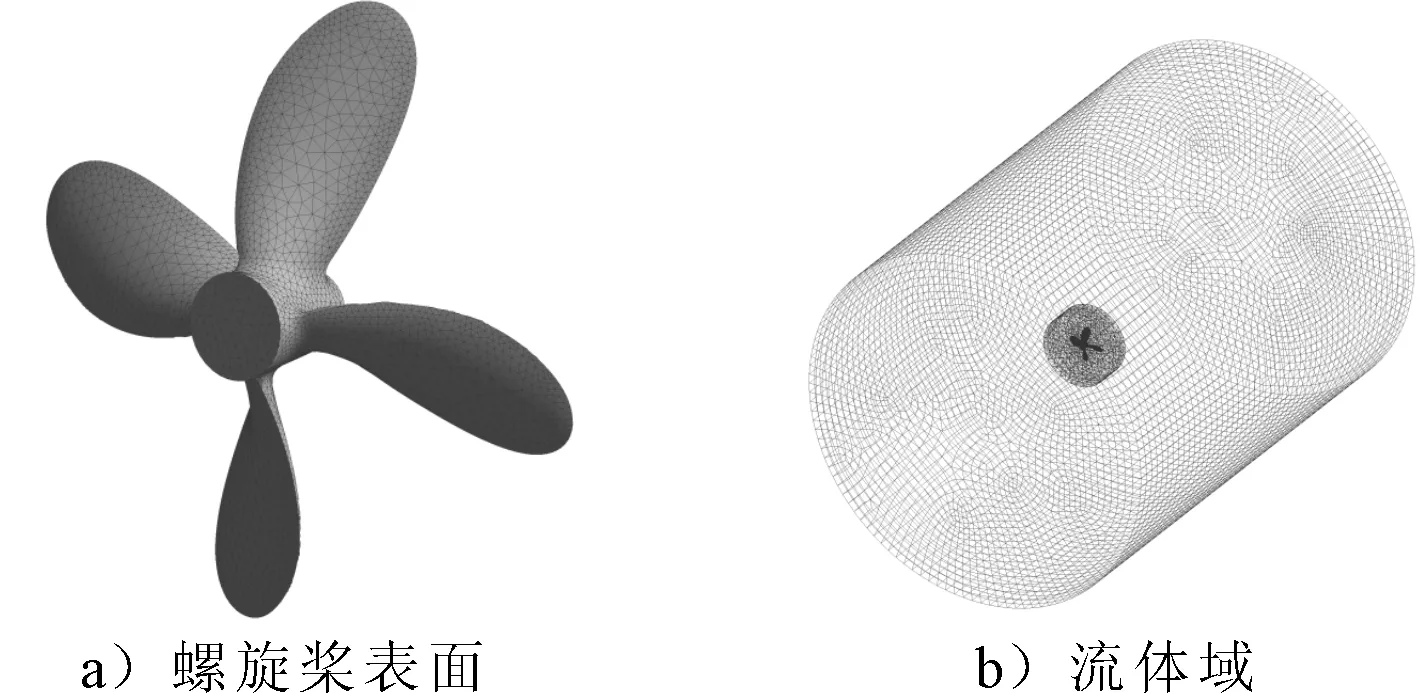
图2 网格模型

流场湍流模型采用标准k-ε模型，进口边界为速度进口，给定进速系数；出口采用压力出口，压力为常数；螺旋桨和轮毂部分表面设置为无滑移、不可穿透壁面，外部边界设置为开放边界.旋转域的运动形式为MRF，绕Z轴旋转；固定域和螺旋桨设置为静止.

2.3 结构域模型及边界条件设置

螺旋桨与轴系的组合模型采用四面体非结构化划分，网格划分后的有限元模型见图3.轴承采用BEARING进行Body-Ground连接，考虑弹性支撑，水平刚度和垂直刚度均为4.6×109N/m，不考虑交叉刚度.

图3 结构的受力与约束

对于轴桨组合在空气中的模态分析，可以分为有预应力和无预应力两种情况考虑.在进行水压力作为预应力的模态分析时，将轴系近主机端进行全约束，通过流固耦合面，将CFX中桨叶在流体域中所受的压力载荷施加到对应固体域的桨叶上；离心力通过对系统设置旋转速度来进行载荷的施加.

2.4 湿模态分析模型网格划分与边界条件设置

为了获得水中模态分布，水体域的建模是关键.轴桨组合结构在运转时，仅有螺旋桨部分和水有直接接触，据此建立水体域三维模型将螺旋桨包围起来[8].考虑到螺旋桨在水域中的实际情况以及计算工作量的大小，最终选取五倍螺旋桨半径的包裹体.为实现固体域和流体域之间的网格匹配，使用 From new part命令将螺旋桨和流场区域合成一个部分，最终水体域模型见图4.

图4 水体域三维模型

采用Fluid220和Fluid221高阶单元作为流体域单元，采用缩减积分控制；而对流固耦合面的固体积分则采用完全积分法，Workbench默认采用Solid186和Solid187单元；强制程序保留单元边线上的中线，以保证在网格划分过程中产生一致的高阶单元，并对水体域网格进行无关性验证[9].

给水体域、与固体域接触的水域边界以及水体域外边界分别设定单元集，名为water，interface，pressure.固体域的材料在Workbench中定义，流体域材料属性的添加需要通过命令流的方式实现；水体密度为1 000 kg/m3，水中声速设为1 500 m/s，水域外边界压力自由度为零，使传出的压力波到达水体域边界时被“吸收”，可以实现无反射边界条件，从而模拟无限流场域.通过插入相关的APDL命令流，采用非对称分析法，求解其前十阶模态.

3 计算结果与分析

3.1 定常水动力载荷计算

进速系数J分别取0.3，0.4，0.5，0.6，0.7，由CFX数值模拟得到螺旋桨所受到的力和力矩值，通过换算得到推力系数kt、转矩系数kq和敞水效率ηo，见图5.

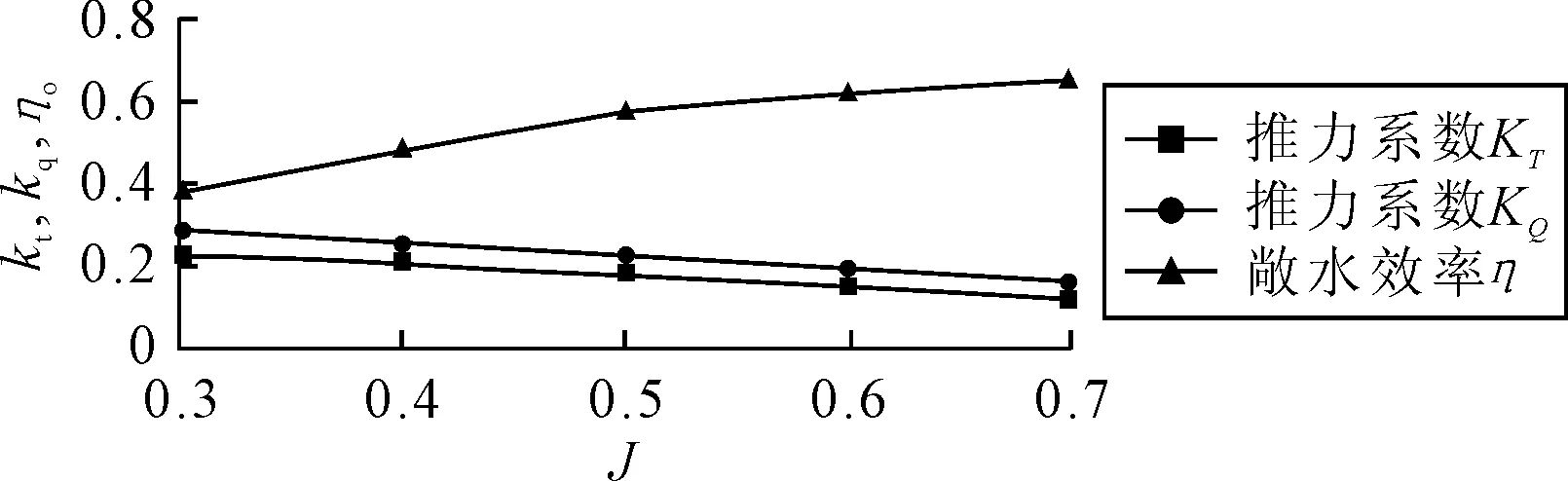
图5 敞水性能曲线

由图5可知，随着进速系数J的增大，推力和扭矩均降低，敞水效率ηo增大，计算结果与图谱结果较吻合.J=0.3时，推力与转矩较大，表3列出了此时螺旋桨所受力与力矩.

表3 螺旋桨所受的力和力矩

由表3可知，螺旋桨在轴向受到了较大的推力和扭矩，X和Y方向由于叶片的均匀分布而受力动平衡.

3.2 流场压力对结构振动影响分析

通过流固耦合面，将J=0.3时流体域叶片的表面压力施加到对应固体域叶片上，计算其各阶固有频率，并与在空气中的自由振动固有频率相比较，见表4.

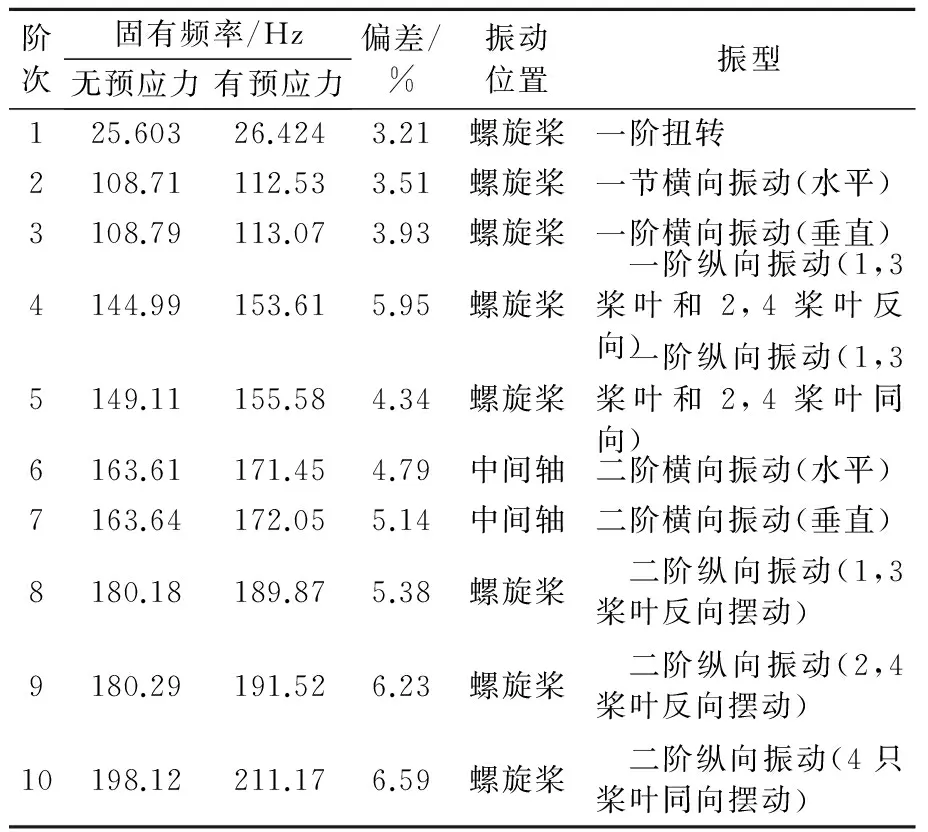
表4 预应力对固有频率影响对比

由表4可知，预应力下模态固有频率均有所提高，变化率为3.21%～6.59%，同时变化率随着阶数上升而增加.这表明流场介质压力提高了结构的刚度，从而提高了各阶固有频率，但是固有频率增长幅度不大.

轴桨组合的低阶振动主要体现在螺旋桨处，随着阶数上升，振动的最大位移向轴系转移.其中一阶为扭转振动，具体表现为螺旋桨绕轴线扭转；二阶和三阶为横向振动，具体表现为螺旋桨在相互垂直两方向上的横向振动；三阶和四阶为纵向振动，具体表现为螺旋桨桨叶纵向摆动，其中三阶为1,3桨叶与2,4桨叶反向摆动；四阶为1,2,3,4桨叶同向摆动.

轴桨组合模型固有模态分析的振型与加载预应力的情况下几乎一致，且第2阶与第3阶、第4阶与第5阶阵型相同，只是方向不同.由于篇幅有限，文中只列出考虑预应力的第1，2，4，6阶干模态振型图，见图6.

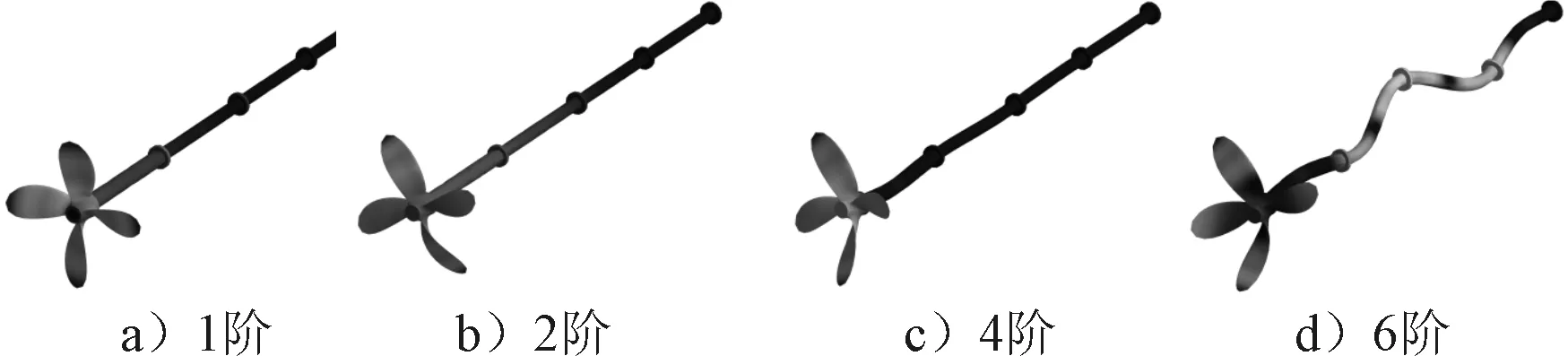
图6 考虑预应力的干模态前四阶振型图

3.3 考虑流场压力的干湿模态对比

通过在Workbench中插入APDL命令流，完成对外部水体的边界条件设置，计算轴桨组合在水中的模态分布.图7为考虑预应力情况下水中、空气中的前十阶固有频率对比，图8为考虑预应力的第1，2，4，6阶湿模态振型图.

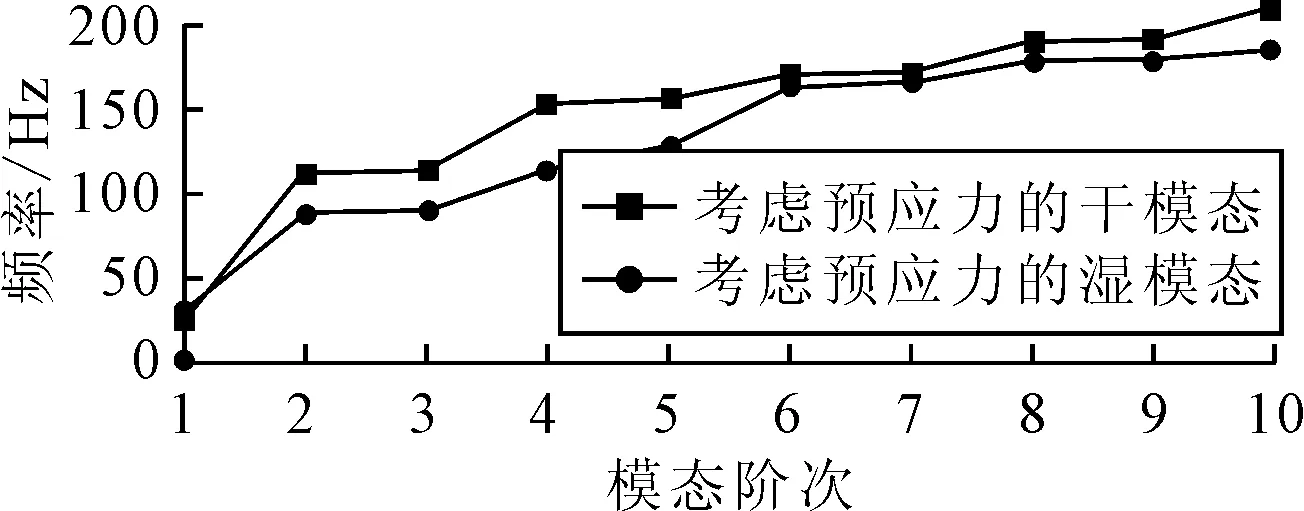
图7 水中、空气中的前10阶固有频率对比

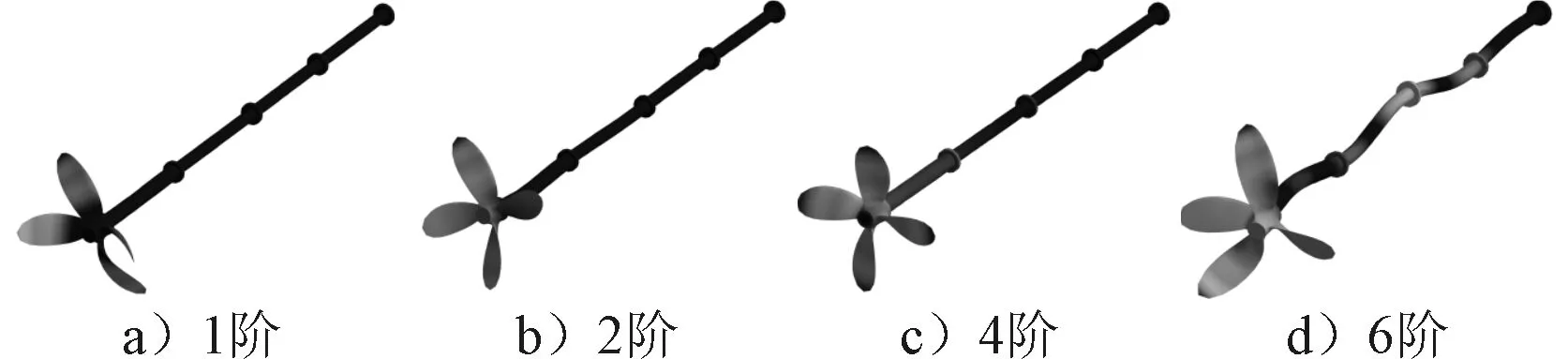
图8 湿模态前四阶振型图

由图7可知，除了第1阶的扭转振动以外，系统在水中的各阶固有频率比在空气中都有了明显降低，这与文献[3]的计算结果基本一致.从附加质量理论来看，水体由于振动而消耗了部分动能，因此轴桨组合系统自身的动能减少，导致其在水中的各阶固有频率均降低.这是由于系统的各阶振动各不相同，因此对水体做的功也不同，所以各阶固有频率降低系数也不同.

比较图8和图6可知，轴桨组合在水中和空气中振型大体相似，但是湿模态各阶固有振动幅度均低于干模态，但此作用随着频率的升高而减弱.这是由于螺旋桨周围的水体的阻尼作用的存在，整个系统的能量发生耗散，因此系统在水中振动的幅值比在空气中振动时幅值小，且随着阶次的上升，差距越来越大.

4 结 论

文中运用流固耦合技术，考虑轴桨组合在受到水压力载荷作为预应力的模态分布情况，并通过在ANSYS Workbench中插入APDL命令，计算螺旋桨在水中时，组合结构的模态，并对比了空气中的固有频率及振型,主要结论如下.

1) 流场压力会造成轴桨结构应力刚化，进而提高振动固有频率，但是影响不明显.

2) 水介质对于轴桨结构振动影响较大，附水质量明显降低结构的固有频率，水介质的阻尼作用降低各阶振动的振幅，且随着阶次的上升，阻尼作用增强.

[1] 翁长俭.我国船舶振动冲击与噪声研究近年进展[J].中国造船，2001,42(3):68-74.

[2] 周春良.船舶轴系振动研究[D].哈尔滨：哈尔滨工程大学,2006.

[3] OLEK C Z, ROBERT L T. Review of the finite element method for solid and structural mechanics[J]. Journal of Engineering Mechanics，2006,132(12):1400-1405.

[4] MAURO C, NICOLE J K. Free vibrational characteristics of isotropic coupled cylindrical-conical shell[J]. Journal of Sound and Vibration，2010,329(6):733-751.

[5] 娄本强.螺旋桨桨叶流固耦合动力分析与试验研究[D].大连：大连理工大学,2008.

[6] 刘强，王永生，董蕾，等.船用螺旋桨振动特性数值计算与分析[J].海军工程大学学报，2016,28(3):17-23.

[7] 施卫东，郭艳磊，张德胜，等.大型潜水轴流泵转子部件湿模态数值模拟[J].农业工程学报，2013(24):72-78.

[8] 任弘.螺旋桨水弹性振动及噪声分析[D].大连：大连海事大学,2015.

[9] 张新，郑源，钱钧，等.基于流固耦合的卧式轴流泵叶轮模态分析[J].水电能源科学，2015(7):164-167.

Influence of Aqueous Medium on the Vibration Modality of Shaft-propeller System in Ship

LIXiaojun1)ZHUHanhua1)XUHaoran1)WUJidong2)XIONGWei2)

(SchoolofEnergyandPowerEngineering,WuhanUniversityofTechnology,Wuhan430063,China)1)(WuchangShipbuildingIndustryGroupCompanyLimited,Wuhan430060,China)2)

In order to study the impact of aqueous medium on the vibration modality of shaft-propeller structure in ship, the vibration modality of one shaft-propeller system in aqueous medium was analyzed by ANSYS WORKBENCH software based on the fluid-structure interaction dynamics equation. The one-way coupling method was used to calculate the impact of pre-stress in flow on the vibration modal of the shaft-propeller system. And the modal distributions were calculated separately in air and water considering flow pre-stress through the coupling APDL command in Workbench. The results show that the pre-stress in flow improves the stiffness of structure slightly, and the natural frequency increases slightly. Additional water mass decreases the natural frequency of the structures obviously, but the modal order in air and in water are the same. Aqueous medium damping decreases the amplitude of the natural frequency.

ship shafting; propeller; vibration; aqueous medium; fluid-structure interaction

U664.21

10.3963/j.issn.2095-3844.2017.06.023

2017-05-15

李小军(1994—)：男，硕士生，主要研究领域为船舶推进技术

*国家自然科学基金重点项目资助(51139005)