让学生学会提出问题——基于正方形背景下问题探究的教学实践

傅瑞琦

（浙江省金华市教育局教研室）

让学生学会提出问题
——基于正方形背景下问题探究的教学实践

傅瑞琦

（浙江省金华市教育局教研室）

提出问题是学生在数学学习过程中发现问题、解决问题的主要途径，是数学学习的一种认知策略，也是一种有效的学习方式.文章以正方形背景下动点探究的课例实践为例，引导学生经历问题探究，聚焦思想方法，培养问题意识，最终掌握提出问题的角度、方法和策略，使“有效启发学生思考”赋予更深刻的内涵.

设计问题；经历探究；学会提问

近期，在一次“有效启发学生思考”主题活动中，笔者以正方形背景下动点探究为载体，上了一节“说说你的发现”的拓展性课程，让学生在探究中发现问题、提出问题，把平时相对独立的知识，以再现、整理、归纳和概括的方式串起来，加深学生对该知识的理解和把握，达到唤醒知识、方法再建和思想升华的学习目的.特别是笔者的适时介入，引导学生将问题分类，在关注研究的方法、思考的顺序、问题间的联系上，让学生提出更有价值、更有思维深度的问题，给“有效启发学生思考”赋予了更深刻的内涵.

一、过程再现

问题背景：如图1，正方形ABCD边长为4厘米，点P从点A出发，经A—B—C沿正方形的边以2厘米/秒的速度运动，同时，点Q沿DC从点D到点C以1厘米/秒的速度运动，设运动时间为t秒.

图1

画一画：你能画出P，Q这两点运动过程中不同阶段的图形吗？根据这些图形，你能得出什么结论？

学生得出结论有：（1）如图1，当t≤2时，点P在线段AB上；（2）如图2，当t=2时，点P到达点B；（3）如图3，当2≤t≤4时，点P在线段BC上.

图2

图3

写一写：尝试提出一个问题，并思考求解思路（将问题写在卡片纸上，不需要求解）.

几分钟后，黑板上汇总出如下提出的问题.

（1）当t=2时，求△APQ的面积.

（2）当t为何值时，A，P，Q，D四点共圆？

（3）以A为原点、两直角边为坐标轴建立直角坐标系，用含t的代数式表示线段QP的长度.

（4）当t为何值时，△PCQ为等腰三角形？

（5）求△APQ的面积S关于t的函数表达式.

（6）当点P在BC上时，△ABP与△CPQ能否相似？

（7）设S△PQD=y，求y关于t的函数表达式.

（8）当t为何值时，△APQ为直角三角形？

（9）当点P在线段AB上时，连接CP，当t为何值时，四边形APCQ为平行四边形？

……

移一移：移动卡片纸，将你认为同一类问题移到一起，并思考：（1）将问题分为同一类的依据是什么？（2）你能解决这一类问题吗？

学生交流讨论后，将问题分成以下几类.

第一类：（1）；

第二类：（3）（5）（7）；

第三类：（4）（8）（9）；

第四类：（2）（6）；

第五类：（3）.

说一说1：第一类问题有什么特点？类似地，你还能提出什么问题？这些问题是从什么角度提出的？

生1：如图2，当t=2时，可以求出线段AQ和PQ的长，还可以求出tan∠QAP和求S△CPQ的值等.

生2：当t=3时，求∠APQ的度数.

……

学生交流概括：这类问题是从t的具体数值得到点P，Q的特殊位置，可以从线段的长、角的大小（或三角函数值）、面积等数量角度提出问题.

说一说2：你能用含t的代数式表示出PQ的长度吗？对第二类问题，你还可以从什么角度来理解这个代数式？进一步可以提出什么问题？

生3：当t≤2时，点P在AB上，当2≤t≤4时，点P在BC上，

生4：还可以从函数的角度提出问题，如线段PQ的最大值是多少？

当t=2时，PQ的最大值是

生5：当t为何值时，

当t=3时，即点P在BC上时，

师：刚才生5提出时，t有一个解.如果t有两个解，PQ的取值范围应该是多少？

生6：当点P在AB上时，当点P在BC上时，所以，如果t有两个解，PQ的取值范围应该是

生7：△APQ的面积S关于t的函数表达式为画出图象（如图4）后就可以结合函数图象提出问题，如t为何值时，△APQ的面积最大？当2≤t≤4时，△APQ的面积S有何变化趋势？当S=4时，求t的值，等等.

学生交流概括：第二类问题是写出代数式后，转化为函数问题，可以从函数概念、图象和性质等角度进一步提出问题.

说一说3：你能解决问题（4）吗？该问题是从什么角度提出的？能否类似提出问题？针对平行四边形、直角三角形的图形特点，你能从其他的角度提出问题吗？

图4

生8：对问题（4），当点P在AB上时，如图5所示，连接PC，过点P作PH⊥DC，由QC=2PB，得出4-t=2(4-2t).解得所以当时，△PCQ是等腰三角形.

图5

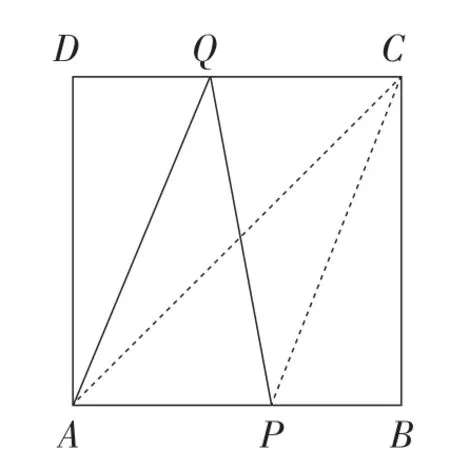
图6

生9：对于问题（9）,还可以这样提出问题：（1）如图6，当t为何值时，线段PQ与AC互相平分？（2）当t为何值时，AQ∥PC？

生10：对于问题（8），也可以改为问题：当t为何值时，AP⊥PQ？

学生交流概括：从三角形、四边形形状判定等角度提出了问题，类似地，可以从图形的位置关系，如垂直、平行等角度提出问题.

说一说4：你能解决问题（6）吗？在求解过程中你有什么发现？该问题是从什么角度提出的？能否类似提出问题？

生11：当点P在BC上时，若△ABP∽△CPQ，则有解得t=3.

生12：我发现，当t=3时，△APQ也是直角三角形，此时这时△APQ与△ABP和△CPQ都相似.从而提出问题：当t为何值时，△APQ与△ABP和△CPQ都相似？

生13：这是从图形之间的关系角度提出问题，类似可以提出，当t为何值时，△ADQ≌△QCP？

当t=2时，即点P在点B处时，△ADQ≌△QCP.

师：还可以从什么角度提出问题？

生14：从线段的数量关系提问.当t为何值时，DQ=2PB？

当点P在AB上时，有t=2(4-2t)，即当点P在BC上时，t=2()8-2t，即

生15：从图形面积的倍数角度提问.如果点P在BC上，当t为何值时，S△ADQ=2S△ABP？

学生交流概括：从图形形状、数量关系等角度提出问题,图形形状、角度有三角形相似、全等，等等；数量关系角度有线段的倍数关系、图形面积等等量关系.

说一说5：问题（3）建立了直角坐标系后，借助坐标系，可以联系哪些知识？对动点P，Q，你进一步可以提出什么问题？结合画出的图形，你可以得到什么结论？

生16：可以用含t的代数式表示点P，Q的坐标，求直线PQ的函数表达式等.

生17：当点P在AB边上时，如图7所示，点P，Q的坐标分别为P(2t，0)，Q(t，4)，直线PQ的函数表达式是y=kx+8；当点P在BC边上时，如图8所示，点P，Q的坐标分别为P(4，2t-4)，Q(t，4)，直线PQ的函数表达式是y=-2x+b.

图7

图8

生18：观察直线PQ的函数表达式，如图7所示，当点P在AB上时.（1）直线PQ是否经过一定点？

过定点(0，8).

（2）求PM与AQ的数量关系.

PM=2AQ.

理一理：通过这节课的复习，试着说说对提出问题的理解，从提出问题的角度、方法去总结.

学生交流后汇总出如下几点.

（1）提出问题角度：①给出t的具体数值，求线段长度、图形面积等；②用含t的代数式表示其他量，写成函数表达式；③图形形状，如三角形形状，特殊四边形的存在性问题；④图形之间的关系，如平行、垂直、全等、相似等；⑤建立直角坐标系后联系函数等.

（2）提出问题过程：画出图形，表达问题，猜测问题，验证问题.

课外拓展：在原问题背景下，如果作PQ的垂直平分线，与正方形ABCD两边交于点E，F，在点P，Q的运动过程中，试提出一个与点E，F相关的问题.

图9

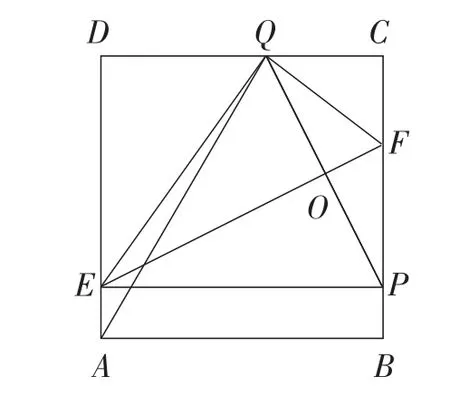
图10

参考问题:

（1）如图9，点P在AB边上时，当t为多少时，四边形EPFQ是正方形？

（2）如图10，点P在BC边上时，当t为多少时，EP∥AB？

（3）在点P，Q的运动过程中，设四边形EPFQ的面积为y，求y关于t的函数表达式.

参考答案：

（3）当t≤2时，点P在AB上，

当2≤t≤4时，点P在BC上，y=5()4-t.

二、教学思考

1.引导聚焦，进一步发展学生的思维

创新思维必须经历两个过程，即发散和聚焦.给出问题背景让学生通过“画一画”“写一写”提出的问题，是零碎、杂乱和发散的，都是学生凭借自己对这一基本图形、相关的知识，以及背后蕴含的基本结论的理解，提出一些自己能够解决的问题.通过“移一移”，让学生对问题进行分类梳理，引导学生共同关注同一类问题.在“说一说”对每一类问题的探究过程中，共同聚焦问题的求解思路，求解过程中的发现，该类问题提出的角度、方法，以及尝试进一步提出问题等，经历了求解发现、模仿提问、概括总结的过程，并完成拓展提问，实现了“学答”到“学问”的真正转变，进一步发展了学生的深度思维.

2.经历探究，让学生真正体会知识的发展与联系

本课例的教学，显著特点是以问引问，激疑导思，引导学生关注提出问题的角度和方法，让数学知识的产生自然而合理.“画一画”让学生画出图形，操作中直观领会运动的过程和图形变化规律；“移一移”引导学生对杂乱无章的问题进行分类，对分类依据的思考，引导学生对同伴提出的问题进行对比，为自己进一步提出问题拓宽思路；“说一说”分别从问题解决、设问角度、研究后续、进一步提出问题等展开教学活动，如“说一说2”中，让学生感悟代数式与函数表达式的一致性，学生求出函数表达式后就能从函数研究的方法和角度进一步设问，如已知t求y的值，已知y的值求t，以及从y的增减性、图象变化等角度提出问题，很自然地让学生联系相关知识、思想方法，积累学习经验；“理一理”从设问角度、联系知识、思想方法等层面来总结概括，在深入思考的过程中，深化对数学知识的理解，规范思维的逻辑，做到思之有法，为以后提出问题、解决问题提供了思路和方法.

通过以上环节的教学活动，让学生充分经历了“动手操作—自主探究—合作交流—归纳概括—拓展应用”的过程，真正体会正方形背景下相关知识的联系、发展和应用.

3.设计问题，引导学生的提问有序展开

提出问题是学生进行数学思考的表现，而问题的深度、广度，则体现学生思维发展的长度.要让学生走的更远，需要学生积极参与到每一个学习活动过程中.这就需要设置符合学生认知规律的系列问题，在一个不断进行提出问题、逐步探索、解决问题的过程中，让学生体验、发现和归纳，以及解决问题的思维方法，进一步学会提出问题.

如第三类问题研究过程中，“你能解决问题（4）吗？”在等腰三角形存在条件的探究中，感受转化方程求解的思路；“该问题是从什么角度提出的？”引导学生及时总结，为下一步提出问题指出方向；“类似地，你还能提出其他问题吗？”让学生在观察中寻找类似图形，浅层次的进行模仿提问；“针对平行四边形、直角三角形的图形特点，你能从另外的角度提出问题吗？”引导学生观察图形与正方形的联系，学生自然产生从另外四点是否也是平行四边形进行猜测，有了这些铺垫，学生就能够从三角形拓展到四边形角度提出问题，从平行四边形，联系线段相等，关注对边平行，从直角三角形，联系两直线垂直，自然过渡到引导学生从图形的位置关系提出问题，让学生感受到各角度提问的密切关联.当学生提出建立直角坐标系时，“说一说5”提出“借助坐标系，可以联系哪些知识？”问题的引导不仅让学生去求点的坐标、直线的函数表达式，更重要的是感受从代数角度研究几何问题的方法，拓宽学生视野，让提出问题有更广阔的空间.

在一组有层次、有梯度的问题引导下，学生思维循序渐进发展，在学生不断提出问题、解决问题的过程中，让学生充分感受到有序的数学思考，激活思维，学会提出更有价值的问题.

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］教育部基础教育课程教材专家工作委员会．《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.

［3］章建跃.中学数学课改的十个论题［J］.中学数学教学参考（上旬），2010（3）：2-5.

［4］史宁中.注重“过程”中的教育：《义务教育数学课程标准》修订的若干思考［J］.人民教育，2012（7）：32-37.

［5］罗增儒.解题分析的理念与实践［J］.中学数学教学参考（中旬），2009（4）：9-13.

2017—09—18

傅瑞琦（1966—），男，中学高级教师，主要从事初中数学教育教学及命题研究.