频域匹配滤波-FFT联合捕获算法*

欧春湘，吴智杰

(北京遥感设备研究所，北京 100854)

0 引言

由于电磁波的空间传输延时，以及收发机间相对运动所导致的频率多普勒效应，无线电信号接收时需要进行定时同步和载波同步。捕获是指在时间和频率上分别设置固定的步进对码相位和多普勒频率进行二维搜索相关峰值[1-3]。对于直扩序列的快速捕获主要有2种技术途径。一种是在时域上进行伪码和载波的串行搜索、时域匹配滤波器法[2-5];另一种是在频域上利用快速傅立叶变换(fast fourier transform，FFT)和快速傅立叶逆变换(inverse fast fourier transform，IFFT)计算多普勒频移估计和码相位估计。传统的捕获方法主要有滑动相关法、时域匹配滤波法、频域匹配滤波法、平均相关捕获算法、折叠匹配滤波法和PMF-FFT(partial matched filtering)部分匹配滤波法等[6-10]。本文提出的频域匹配滤波-FFT联合捕获法不仅实现简单且大幅度地提高了多普勒频率的估计精度。

1 频域匹配滤波

1.1 基本原理

假设伪码长度为N，接收到的伪码序列为c(n)，本地复制伪码序列为c′(n)，相关值为corr(n)，则有

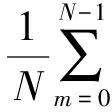
(1)

对相关值corr(n)进行离散傅里叶变换：

(2)

式中：C(k)和C′(k)分别为c(n)和c′(n)的离散傅里叶变换;C′*(k)代表复数C′(k)的共轭。

C(k)=FFT(c(n)),

(3)

C′(k)=FFT(c′(n)).

(4)

式(2)表明2个码序列c(n)和c′(n)在时域做相关运算，在频域内相当于一个序列的离散傅里叶变换C(k)与另一个序列的离散傅里叶变换的共轭值C′(k)相乘。因此CORR(k)的离散傅里叶反变换正好是2个码序列在各个码相位处的相关值。

corr(n)=IFFT(CORR(k)).

(5)

1.2 实现流程

捕获过程需要完成载波多普勒和伪码相位的二维扫描[11]，如图1所示，fbin和tbin分别为频率搜索步进和码相位搜索步进。当在第i行第j列得到相关峰值且超过门限时，则得到与接收信号一致的载波多普勒fd(i)和码相位值p(j)，完成了码并行捕获。如何按照一定的策略快速地遍历所有的载波多普勒频点和码相位是捕获的关键[12-14]。频率匹配滤波法就是在每一次扫描一个载波多普勒频率，在该频点按照式(2)～(4)完成伪码的快速相关，实现流程图如图2所示。

图1 捕获二维搜索图Fig.1 Acquisition searching map in two dimension

图2 频谱匹配滤波原理图Fig.2 Construction of frequency domain matching filter

ui(t)为接收信号，载波NCO产生查找地址，通过查找正余弦查找表得到本地同相载波uoc(t)和正交载波uos(t)，分别表示为

(6)

(7)

(8)

式中:a和a′分别为接收信号和本地载波的幅值;d(t)为调制的数据;c(t)为伪码序列;ωi和ωo分别为接收到的载波频率和本地载波频率;φ为接收信号的初相位。

正交下变频后同相支路再经过低通滤波器滤除高频分量后得到

i(t)=ui(t)uoc(t)=2aa′d(t)c(t)·

cos(ωit+φ)cos(ωot)=

aa′d(t)c(t){cos[(ωi+ωo)t+φ]+

aa′d(t)c(t)cos[(ωi-ωo)t+φ].

(9)

正交下变频后正交支路再经过低通滤波器滤除高频分量后得到

q(t)=ui(t)uos(t)=2aa′d(t)c(t)·

cos(ωit+φ)sin(ωot)=

aa′d(t)c(t){sin[(ωi+ωo)t+φ]-

-aa′d(t)c(t)sin[(ωi-ωo)t+φ].

(10)

I和Q 2个支路合并成i(t)+j·q(t)后做FFT运算，再与伪码FFT共轭相乘，做FFT逆变换得到各个伪码相位上的相关值，相关运算后得到

uout(t)=aa′d(t)R(τ)e-j(Δωt+φ),

(11)

式中:R(τ)为接收到的伪码c(t)与本地伪码c′(t)的相关值;τ为c(t)与c′(t)的时间差;Δω=ωi-ωo为接收到的载波和本地载波的频率差。

对uout(t)取模进行幅值判断，若大于门限值则表示捕获成功，否则继续下一个频点重复上述过程。因为伪码的强相关性和弱互相关性，当τ不为零时，R(τ)将严重衰减使得幅值减小；当Δω不为零时，由指数函数的衰减性可知，幅值将成指数衰减[15-16]。因此由式(10)可知，只有当载波和码相位都严格对齐时才能得到峰值，捕获到峰值的同时得到了载波多普勒值和伪码相位值。

2 联合捕获法

联合捕获法是基于频域匹配滤波法的一种捕获方法，连续k个码周期做相关运算，对同相位的k

个相关值做二次FFT运算，具体的实现方法如图3所示。

第1步，利用FFT运算求解输入信号的频域表示，FFT的频移特性即频域移相等效时域相乘的特性如式(12)所示，因此在各支路上对N1点输出进行2N2+1次移相，等效于在多普勒频率范围[-Fd，Fd](kHz)内对输入信号进行2N2+1路并行下变频。

若FFT[x(n)]=X(k)，则

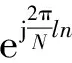
(12)

相关积分时间Tcoh为一个码周期时间，将一个码周期划分成N1个搜索单元,

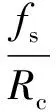
(13)

式中：fs为采样频率；Rc为码速率;L为码周期。

图3 频域匹配滤波-FFT联合捕获法实现流程Fig.3 Construction of frequency domain matching filter and FFT union acquisition

(14)

将多普勒频率范围[-Fd，Fd](kHz)分成2N2+1个搜索单元，每个搜索频率记为fdi，本地载波记为CLi(t)，即

(15)

fdi=i·fbin,

i=-N2，-(N2-1)，…，0，…，N2,

(16)

CLi(t)=cos(2πfdit)-i·sin(2πfdit),

i=-N2，-(N2-1)，…，0，…，N2,

(17)

式中：[·]表示取整数。

假设输入的基带信号为S1(t)，S1(t)与CLi(t)正交下变频得到基带复信号S2i(t)。

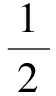
i=-N2，-(N2-1)，…，0，…，N2,

(18)

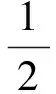
i=-N2，-(N2-1)，…，0，…，N2.

(19)

第2步，2N2+1路下变频信号S2i(t)与原位输出的本地伪码的FFT运算结果共轭相乘，并对输出结果进行IFFT运算，由式(2)可知，该步骤相当于求得各通道上的一个码周期长度的时域相关积分，得到N1(2N2+1)个相关积分值。至此，完成了单个伪码周期内的扫频搜索，频率搜索步进为fbin。

2N2+1通道的第k通道零中频基带信号S2k(t)与本地伪码pn(t)相关累加后得到N1个相关值S3k(l)，采用MSK调制。

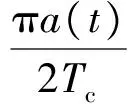
(20)

S3k(l)=S2k(t)⊗pn(t+lTc)=

i(t)⊗pn(t+lTc)+j·q(t)⊗pn(t+lTc)=

I(l)+j·Q(l),

l=0，1，…，N1-1,

(21)

式中:Tc=TL/N1，TL为一个码周期时间。

则

I(l)=i(t)⊗pn(t+lTc)=

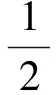
l=0，1，…，N1-1,

(22)

Q(l)=q(t)⊗pn(t++lTc)=

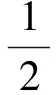
l=0，1，…，N1-1,

(23)

fe=fd-fdi,

(24)

S3k(l)=I(l)+j·Q(l)=

l=0，1，…，N1-1,

(25)

式中:t1为相关起始时刻;ωe=2πfe;R(·)表示自相关函数。

第3步，在连续K个伪码周期上做上述相关运算，每个通道得到KN1个相关值，将KN1值存储在一个K×N1的矩阵X1里。对每一列K个点进行FFT运算，得到K×N1的矩阵X2，等效为对各相位上的相关结果按基带速率进行K次相干累加，理论捕获精度提高为fbin/K。

矩阵X2的第p列为S3k(p)，FFT峰值为v，则

v=K·S3k(p)=

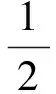
(26)

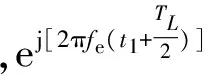
τp+pTc≈0,

(27)

fe=fd-fdi≈0.

(28)

式(27),(28)表示只有当码相位差小于码相位搜索步径，且本地多普勒频率与接收信号的多普勒频率基本保持一致时才会出现相关峰值。

第4步，在总样本为(2N2+1)N1K的基础上，计算相关值的最大值和均值，并得到峰均比。至此，完成了第1轮K个伪码周期的相干累积搜索。

第5步，当连续2次判决输出均过门限Vt，2次捕获结果码片差在码相位搜索步进以内，且频率差在fbin/K以内，则判决成功，启动后续信号处理模块，否则，捕获模块继续搜索。

3 仿真与分析

与理论分析部分的假设相对应，设置基本的数值和仿真环境为：采样频率fs=4 MHz，码速率Rc=2 MHz，码周期L=128，多普勒频偏范围±100 kHz，联合捕获的频率搜索步进为15.625 kHz，码片搜索步进为0.5个码片，相关时间为一个码周期，在连续K=20个伪码周期上做相关运算，每个码相位上得到20个相关值，再补10个0做32点FFT运算。FFT运算提高了相关峰均值，多普勒频率估计精度提高为15.625 kHz/32=488.28 Hz，设置以下2个仿真条件分别进行验证。

设置载波多普勒频率为66.7 kHz，码相位差为155个半码片，不存在跳频同步误差。图4为一个伪码周期的相关峰均值，图5为联合捕获最后一级32点FFT得到的相关峰均值，对比可知，联合捕获得到的相关峰均值明显高于直接相关累加的相关峰均值，提高了检测概率。

图4 频域匹配滤波相关峰值Fig.4 Correlation result of frequency domain matching filter

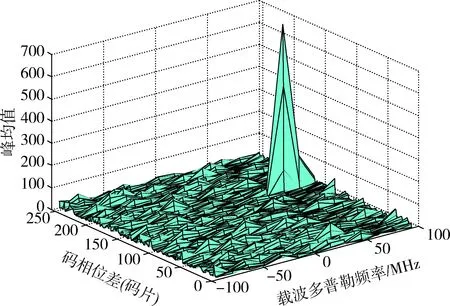
图5 联合捕获相关峰值Fig.5 Correlation result of union acquisition

设置中频信噪比为-15 dB，多普勒频率在±100 kHz范围内，通过仿真得到联合捕获法和频率匹配滤波法的载波多普勒频率估计误差的变化情况，如图6所示。由图6可知，频率匹配滤波法残余的多普勒频偏精度为8 kHz，联合捕获残余的为1 kHz，在捕获精度上明显优于传统频域匹配滤波法。

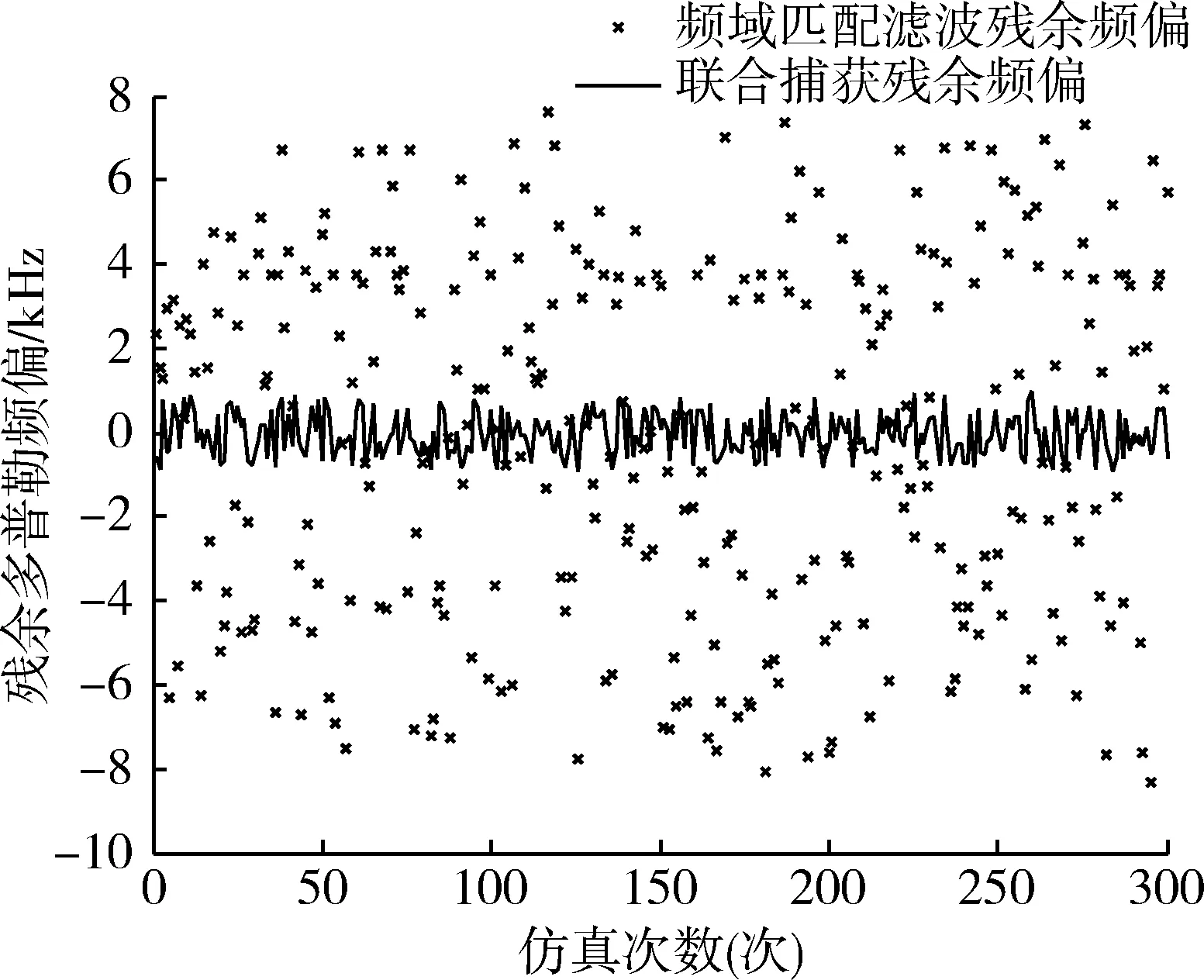
图6 多普勒频率估计误差Fig.6 Estimated error of Doppler frequency

为了得到在±100 kHz多普勒频偏范围内，捕获概率随信噪比的变化，设置多普勒频偏分别为-100,0,100 kHz，得到3条捕获概率随中频输入信噪比变化的曲线如图7所示。由图7可知，随着信噪比的增加捕获概率不断增加，由于位于频率搜索单元的不同频率位置，0和±100 kHz存在2 dB的差别，多普勒频偏为0时在-16 dB捕获概率接近1，多普勒频偏为±100 kHz时在-14 dB捕获概率接近1。

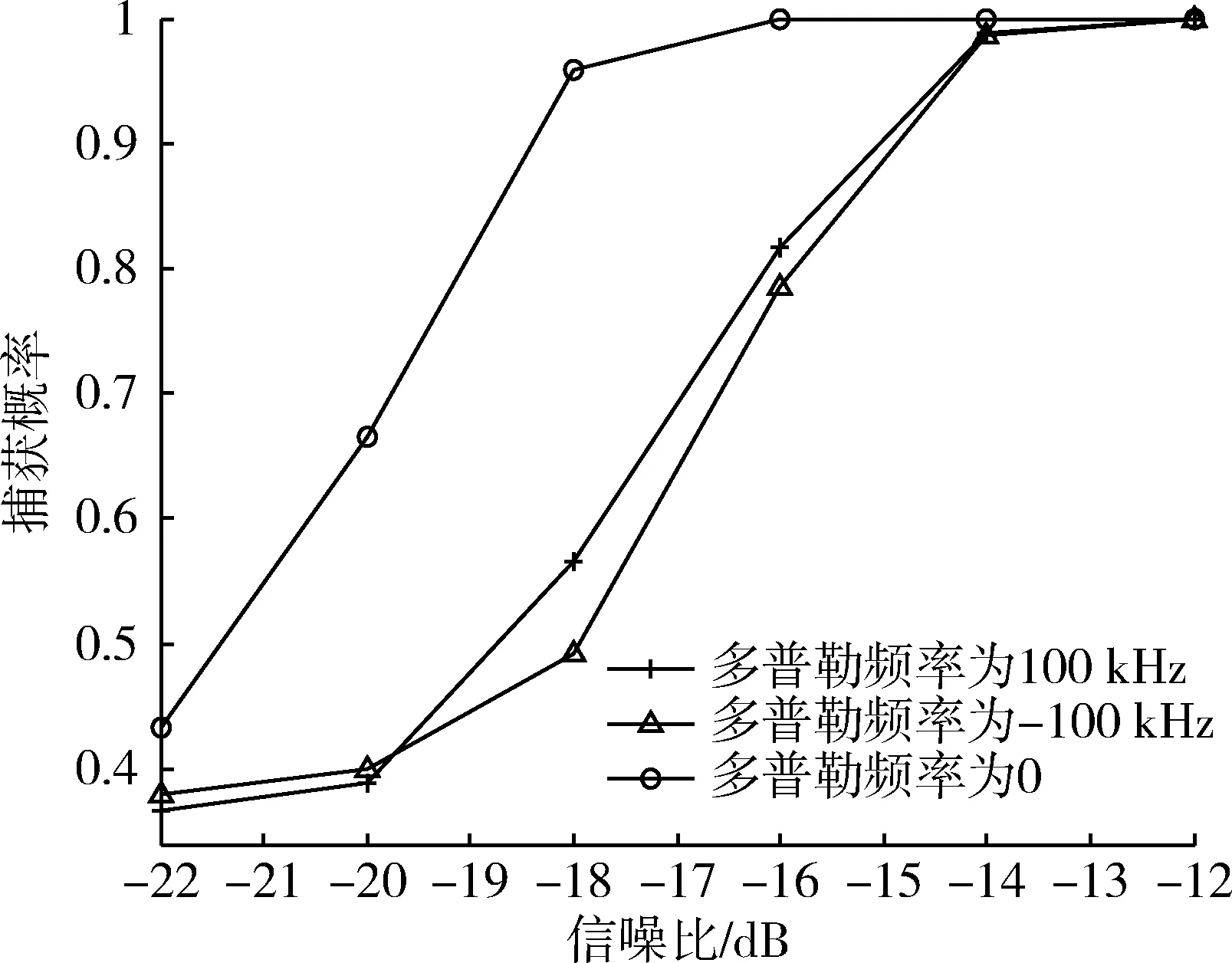
图7 不同信噪比下的捕获概率Fig.7 Acquisition probability in different SNR

4 结束语

频域匹配滤波-FFT联合捕获法在频域匹配滤波的基础上对连续K个相同码相位的相关结果进行二次FFT运算，相当于K次非相干累加。经过实验仿真可知，该方法提高了多普勒频率的估计精度，在信噪比大于-14 dB时捕获概率能达到0.988，多普勒频率的捕获范围能够达到±100 kHz。由此可见，频域匹配滤波-FFT联合捕获法在估计精度和捕获概率上优于传统的频域匹配滤波法。

[1] 王江浩，李署坚.一种改进的伪码捕获方法[J].电子测量技术，2008,31(12)：10-14.

WANG Jiang-hao，LI Shu-jian.Improved Method of Acquisition of Pseudo[J].Electronic Measurement Technology，2008,31(12)：10-14.

[2] 展放，张君昌.数字匹配滤波器在直序扩频快速捕获中的应用[J].航空电子技术，2003，34(3)：15-18.

ZHAN Fang，ZHANG Jun-chang.Application of DFM to DS/SS Rapid Acquisition[J].Avionics Technology，2003，34(3)：15-18.

[3] 金俊坤，吴嗣亮，李菊.基于基2-FFT的伪码快速捕获实现新算法[J].系统工程与电子技术，2005，27(11)：1957-1960.

JIN Jun-kun，WU Si-liang，LI Ju.Implementation of A New Fast PN Code-Acquisition Using Radix-2 FFT[J].Systems Engineering and Electronics，2005，27(11)：1957-1960.

[4] 胡建波，杨莘元，卢满宏.一种基于FFT的高动态扩频信号的快速捕获方法[J].遥测技术，2004，25(6)：19-24.

HU Jian-bo，YANG Xin-yuan，LU Man-hong.An FFT Based Method for Fast Acquisition of High Dynamic DS Spread Spectrum Signals[J].Telemetry & Telecontrol，2004，25(6)：19-24.

[5] 国世超，陈安乐，韩方剑.基于部分匹配滤波的伪码捕获方法研究[J].电子信息对抗技术，2010，25(2)：20-23.

GUO Shi-chao，CHEN An-le，HAN Fang-jian.Pseudo-Noise Code Acquisition Method Based on Partial Matched Filter[J].Electronic Information Warfare Technology，2010，25(2)：20-23.

[6] 黄振，陆建华，杨士中.基于DMF直扩系统捕获性能研究[J].电路与系统学报，2002，7(1)：92-95.

HUANG Zhen，LU Jian-hua，YANG Shi-zhong.Perfor-mance of Acquisition in a Matched-Ffilter for DSSS[J].Journal of Circuits and Systems，2002，7(1)：92-95.

[7] 黄磊，张其善，寇艳红.基于差分码和块处理方法的GPS信号快速捕获算法[J].通信学报，2006，27(8)：14-19.

HUANG Lei，ZHANG Qi-shan，KOU Yan-hong.GPS Signal Fast Acquisition Algorithm Using Differential Code and Block Processing Techniques[J].Journal on Communications，2006，27(8)：14-19.

[8] LIN D，TSUI J.Comparison of Acquisition Methods for Software GPS Receiver[J].Ion GPS，2002，91(5)：2385-2390.

[9] LEE Yong-hwan，TANTARATANA S.Sequential Acqui-sition of PN Sequences for DS/ SS Communications：Design and Performance[J].IEEE Journal on Select Areas in Communications，1992，10(4)：750- 759.

[10] TANIGAWA M，HARA T，FUKUI M，et al.Fast Acquisition and Low Correlation Multi-Component Code[J].IEEE Transactions on Communications，2004，4(1)：2454-2457.

[11] FENG G.Block Processing Techniques for the Global Positioning System[D].Ohio:Ohio University，2003.

[12] ZHU Z.Averaging Correlation for Weak Global Positioning System Signal Processing[D].Ohio:Ohio University，2002.

[13] STARZYK J A，ZHU Z.Averaging Correlation for C/A code Acquisition and Tracking in Frequency Domain[J].MWSCS Conf，2001，12(15)：24-28.

[14] IUNTA G，BENEDETTO F.Spread-Spectrum Code Acquisition in The Presence of Cell Correlation[J].IEEE Transactions on Communications，2007，55 (2)：257-261.

[15] JARI H，IINATTI J.On the Threshold Setting Principles in Code Acquisition of DS-SS Signals[J].IEEE Journal on Selected Areas in Communications，2000，8(1)：62-72.

[16] SIMON M K，OMURA J K，Scholtz R A，et al.Spread Spectrum Communication Handbook[M].Beijing:Post & Telecommunications Press，2002.