巡航飞行航向位置实时跟踪PID控制器设计*

谢晓方，刘家祺,2，孙涛，梁捷

(1. 海军航空工程学院 兵器科学与技术系， 山东 烟台 264001； 2. 中国人民解放军92768部队， 广东 汕头 515828)

0 引言

航迹跟踪控制是飞行任务计划执行的关键环节，现代电传操纵的综合飞行控制系统主要由飞行管理、飞行导引和飞行控制3个子系统组成。飞行管理系统接收地面指挥中心的航路规划方案和导航系统给出的位置信息反馈计算参考航迹和实际航迹，飞行导引系统根据导引律产生飞行控制所需要的期望状态使航迹误差趋于0，飞行控制系统根据期望状态和机载传感器测量实际状态之间的误差产生舵面和推力控制指令。通常航路规划结果是给定的一系列航路点坐标，如果对飞行时间有要求还要给出各个航路点的时刻。文献[1-2]在高度和空速不变的假设下采用B样条插值法拟合水平面内期望航迹，平滑的参考轨迹能减少控制难度和误差。文献[3]将整条航路分为直线飞行和转弯飞行阶段，在导航坐标系下修正侧向航迹偏差，文献[4]给出了侧向加速度补偿算法。文献[5-7]将PID控制器和其他控制方法相结合，提高了控制精度和自适应能力。文献[8-10]采用视线制导算法实现了编队跟踪飞行，但无法有效消除航迹的横向偏差。文献[11]选取参考航迹上一系列固定点作为导航点，假设风速不变设计了速度控制器，设计姿态控制器控制速度坐标系对准导航点。文献[12-14]将航迹跟踪问题转化为对参考航迹上移动虚拟目标的跟踪，通过合理选择虚拟目标间距和速度，使跟踪侧偏距和航向误差趋于0。

PID控制器因为结构简单和易于调试等优点，在控制领域得到了广泛的应用。目前侧向偏差控制算法已比较成熟，本文主要研究影响到达时间的航向距离控制，采用PID控制器解决飞航式飞行器航向位置跟踪问题，为提高存在阵风干扰时的控制精度，根据卫星/惯性组合导航系统反馈的地速和位置信息进行比例积分控制，利用加速度计反馈的加速度信息进行内环微分控制以提高动态跟踪性能。

1 传统空速保持控制巡航飞行

巡航飞行是指起飞行器为执行远距离飞行任务而选择的经济性较好的飞行状态。目前典型巡航飞行方式主要有：马赫数保持巡航、飞行高度保持巡航和发动机额定推力巡航等。

飞行器起飞进入预定巡航起点位置后，即可选择接通自动驾驶仪中的空速保持器或者高度保持器。大多空气动力参数和空速(马赫数)有关，不变的空速可以减少气流对高度等飞行参数的干扰，保证控制器稳定工作，防止出现失速等情况引起安全事故。典型空速保持控制结构[15]如图1所示。

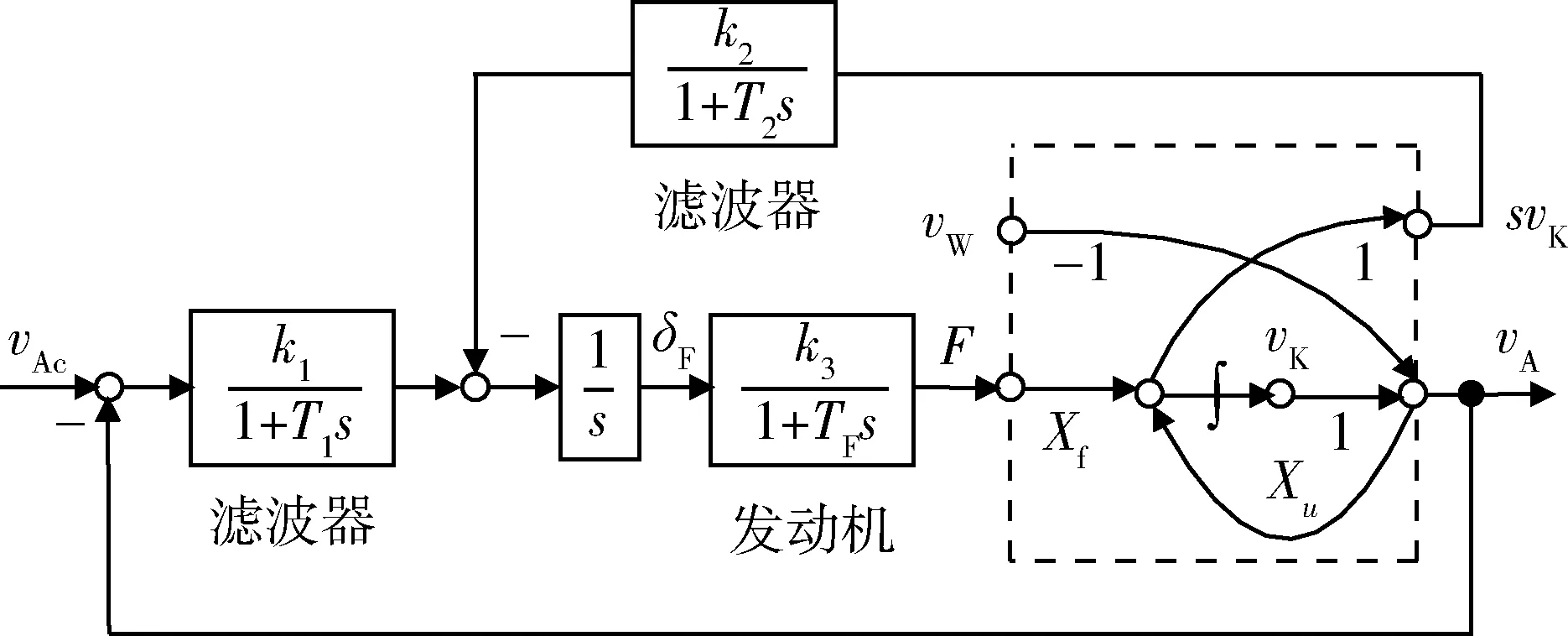
图1 空速保持控制结构图Fig.1 Structure chart of airspeed hold control

图1中，vA为空速，vK为地速，vW为风速，假设这3个速度在同一条水平线上，F为推力，δF为油门信号，vAc为参考空速，Xf为推力质量比，Xu为阻力质量比，发动机近似为增益k3，时间常数TF的一阶系统，空速反馈和加速度反馈经过互补滤波器和积分伺服机构后作为发动机输入信号。

水平风的阶跃变化将无滞后的影响空速，而地速的变化则是迟后发生的，如果把受阵风直接影响的空速信号反馈给推力，推力将会变的非常不平滑，附加互补滤波器能够抑制来自紊流和发动机噪音的高频信号部分，为了补偿风切边的影响和减小稳态空速偏差，推力控制器还要具有积分特性。

虚线框中受控体各变量的拉氏换有以下关系：

(1)

根据式(1)可解算出空速和加速度为

(2)

阵风干扰对空速和地速的作用方程为

(3)

所以，干扰对地速的作用相当于经过一个低通滤波器，而对空速的作用相当于经过一个高通滤波器。从δF处断开系统，开环发动机输入信号

(4)

保持空速时vAc=0，由式(2)和式(4)，得

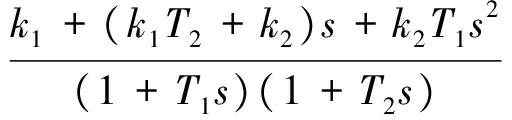
(5)

式中:第1项是除去发动机动态特性以外的系统开环传递函数，其中互补滤波器部分的分母和分子阶数相同，设计滤波器在穿越频率附近相位损失很小，因而它在稳定性方面对控制回路的影响很小。这些滤波器对扰动信号的作用则完全不同，这可由第2项看出，它表征了阵风对发动机输入信号的影响，这个信号在低频范围内应尽量放大，但在发动机所允许的频率以上时应尽快抑制。设计参数满足:

k1T2+k2XuT1=0.

(6)

则有扰动变量vW到油门信号的开环传递函数

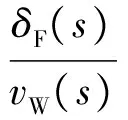
(7)

使得互补滤波器对扰动变量有二阶滞后特性，在正vW时，应增大推力加速飞行保持空速不变，滤波器时间常数满足1-T2/T1>0，即T1>T2。高频阵风信号在高于角频率1/T1和1/T2时将被抑制。

2 改进地速保持控制巡航飞行

通过对空速保持控制分析可知，低频率的干扰容易引起地速改变，这将导致飞行时间难以控制，因此可以考虑用地速反馈来代替空速反馈，实现地速保持，控制结构如图2所示，其中vKc为参考地速。

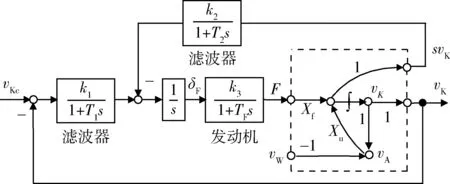
图2 地速保持控制结构图Fig.2 Structure chart of ground speed hold control

由式(2)得被控对象地速和推力及阵风干扰关系:

(8)

发动机油门信号为

(9)

保持地速时vKc=0，则有

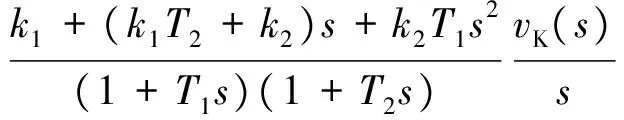
(10)

2个滤波器对推力和干扰的作用是相同的，如果仍像空速保持那样设计对推力相位损失为0，那么对高频干扰就没有抑制效果。考虑到在受控对象中干扰到地速的传递函数本身就具有低通滤波作用，所以地速保持控制中可以去掉这2个滤波器，即T1=T2=0。

显然，地速和加速度反馈经过积分器相当于PI控制器，为保证系统稳定，选择控制参数遵循先内环后外环的顺序，断开加速度和地速反馈回路，得到加速度反馈开环传递函数

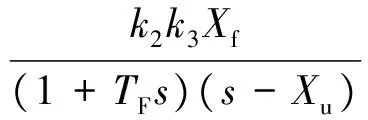
(11)

依据根轨迹选择满足控制性能要求的增益k2后，接通加速度反馈回路，断开地速反馈回路，地速反馈开环传递函数可由梅森公式求得

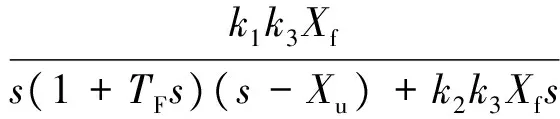
(12)

同样根据该传递函数的根轨迹确定能使系统稳定且具有良好性能的增益k1。

3 航向位置跟踪的PID控制结构

如果要实时跟踪变化的参考位置信号，控制器还必须增加微分环节才能具备良好的动态性能，除了反馈地速和加速度信号外还需要反馈位置信息，即构成PID控制器，在地速保持控制器基础上设计位置跟踪控制器，如图3所示。

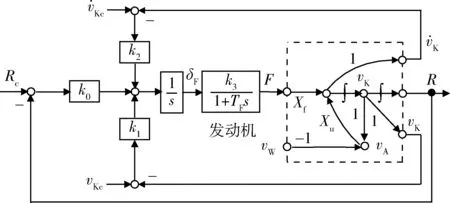
图3 位置跟踪PID控制结构图Fig.3 Structure chart of position tracking PID control

根据式(8)得到位置信号的拉氏变换

(13)

Rc(s)=v0/s2.

(14)

位置跟踪PID控制器的发动机油门信号为

k2svK(s)),

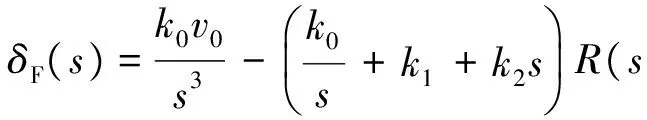
(15)

从干扰信号到油门信号的开环传递函数为

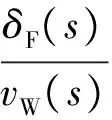
(16)

可以根据该传递函数频率特性设计对干扰信号的抑制动态特性，保证发动机输入信号平静。若将位置反馈断开，系统的开环传递函数为

G0(s)=

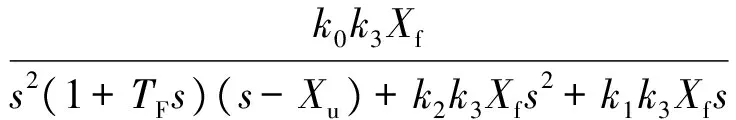
(17)

位置反馈回路为第3层外环，增益k0采用与地速保持控制器相同的根轨迹设计方法确定，增益k1和k2保持不变。

4 仿真校验

某型飞机巡航高度h=1×104m，巡航飞行速度v0=250 m/s，该状态附近线性化空速阻力系数Xu=-0.007 s-1，加速惯性系数Xf=9.8×10-6kg-1。推力增量限制ΔF≤2×104N，时间常数TF=0.1 s，增益k3=1×104。

4.1 地速保持控制器

设置滤波器参数T1=T2=0，断开加速度和地速反馈回路，加速度反馈开环传递函数对应的根轨迹如图4所示。加速度反馈开环传递函数有2个极点，随着反馈增益k2的增加，闭环系统由过阻尼状态向欠阻尼状态转变，k2=25.5为临界阻尼状态，综合考虑稳定性和响应动态特性，选择反馈增益k2=25。

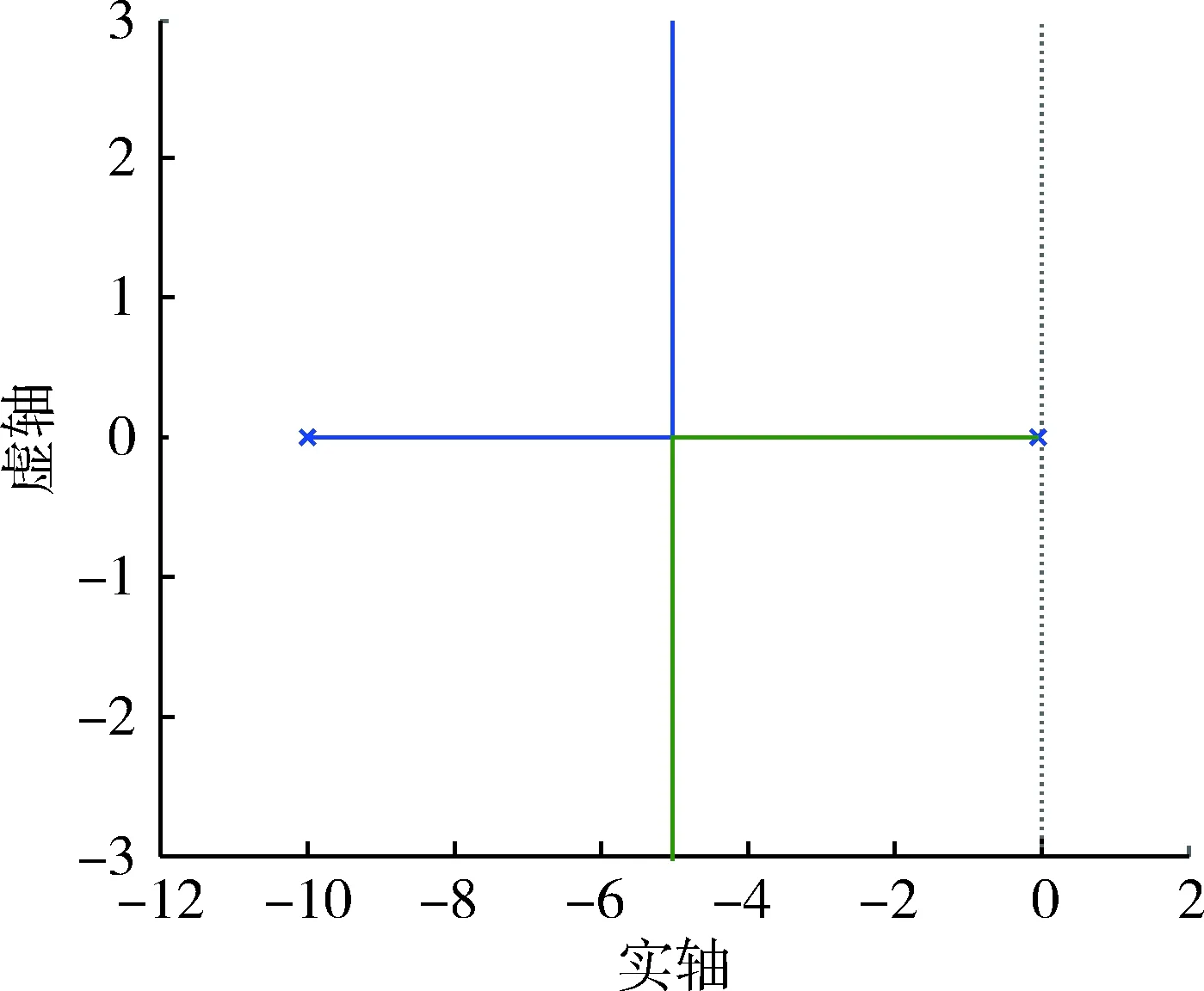
图4 加速度反馈根轨迹Fig.4 Root locus of acceleration feedback

以增益k2=25接通加速度反馈内回路，地速反馈外回路保持断开状态，系统根轨迹如图5所示。地速反馈开环传递函数有3个极点，k1=18.2时为临界阻尼状态，k1=250时为临界稳定状态，为了保证加速过程中推力变化平缓，延缓系统响应时间，选取反馈增益k1=2。

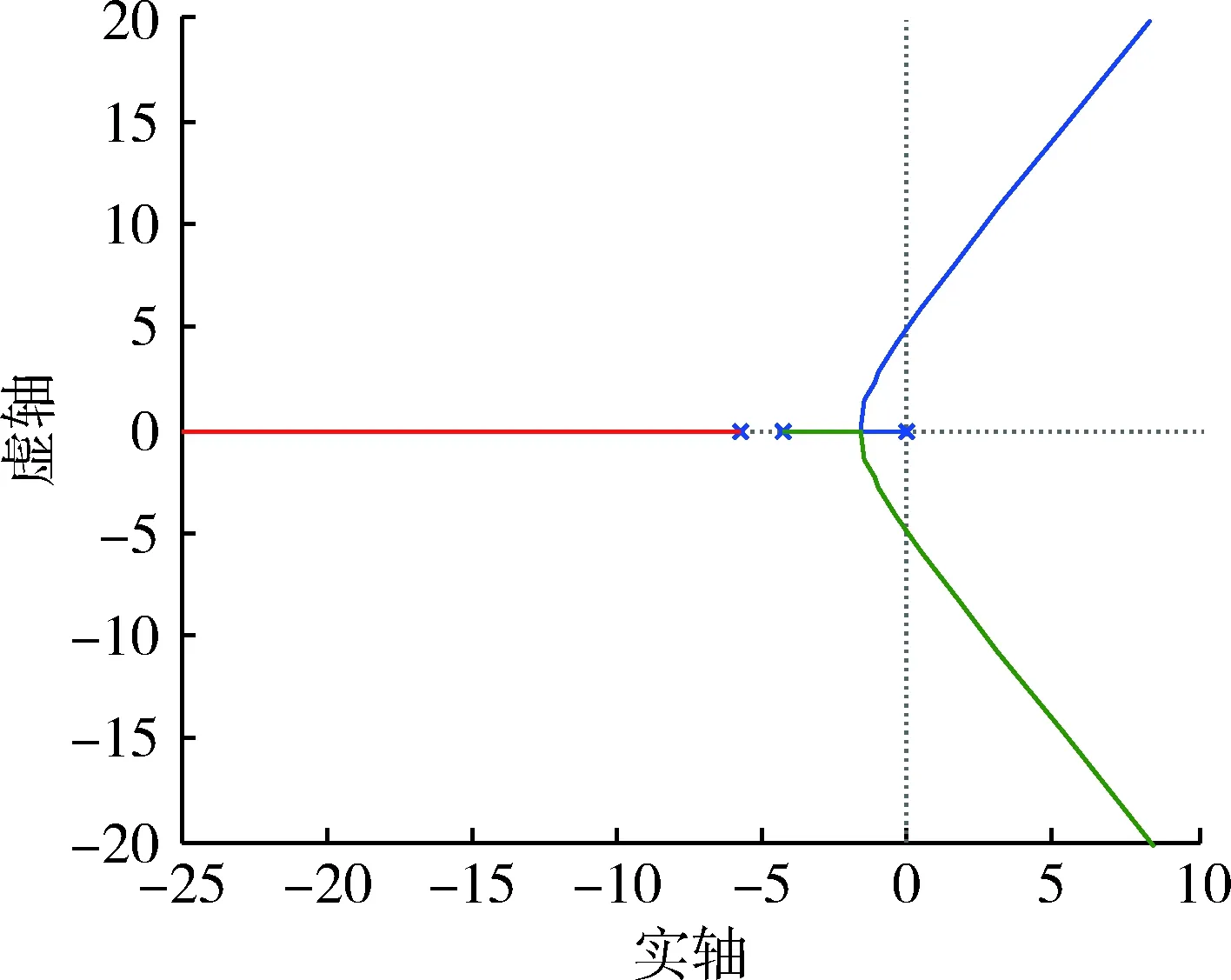
图5 地速反馈根轨迹Fig.5 Root locus of ground speed feedback

为观察控制器的阶跃响应特性，设置参考空速和参考地速为t=10 s时刻开始的幅值2 m/s阶跃信号，即vAc=vKc=2step(t-10)，风干扰为vW=step(t-100)，空速保持控制器和地速保持控制器的响应分别如图6和图7所示。

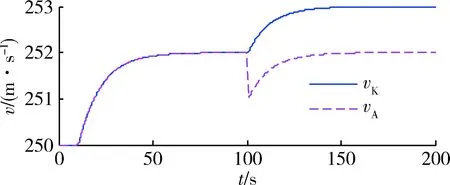
图6 空速保持阶跃响应Fig.6 Step response of airspeed hold

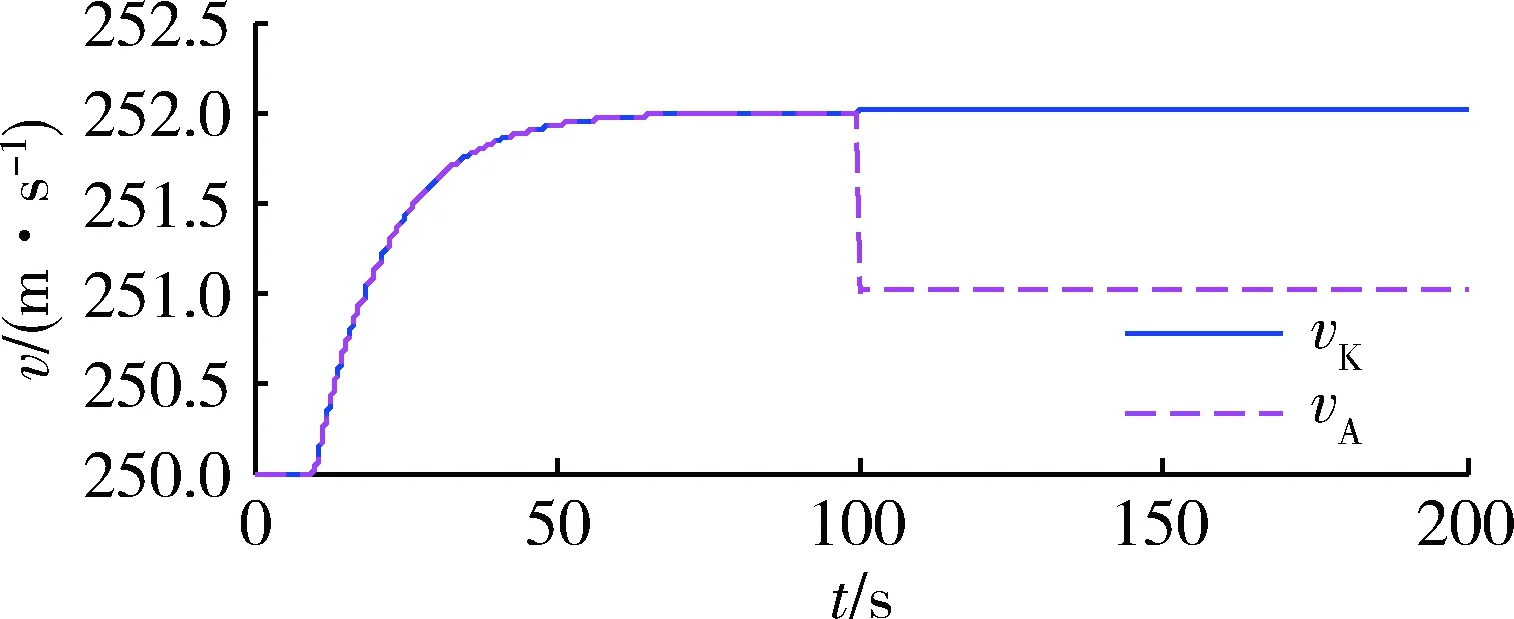
图7 地速保持阶跃响应Fig.7 Step response of ground speed hold

没有干扰的情况下，对于10 s时刻的参考速度阶跃变化，2种控制器的响应是相同的。100 s时刻风速突变几乎瞬时无延迟的引起等量的空速改变，在空速保持控制器的作用下，空速和地速都会增加，稳定后的空速恢复到干扰加入前水平，而地速提高的幅度等于风速增加量；在地速保持控制器的作用下，地速几乎不受影响，而空速降低后保持不变，减小量等于风速增加量。

在传统空速控制方式下，地速受到随机风干扰，整个飞行过程不能被精确控制的，因此到达时间也只能通过预测估计得到；若改为地速控制方式，地速基本不会受到干扰，飞行时间也是精确可控的。

4.2 航向位置跟踪PID控制器

在4.1节设计的地速保持控制器基础上，反馈增益k1和k2保持不变，增加航向位置反馈，根轨迹如图8所示。

图8 航向位置反馈根轨迹Fig.8 Root locus of heading position feedback

位置反馈开环传递函数有4个极点，k0=0.04时为临界阻尼状态，k0=4.3时为临界稳定状态，选取k0=0.05。此时阵风干扰到油门信号传递函数对应的伯德图如图9所示，该传递函数无差度为2，故低频段幅频特性曲线斜率为-40 dB/(°)，穿越频率为0.182 rad/s，大于该频率的高频干扰受到抑制。

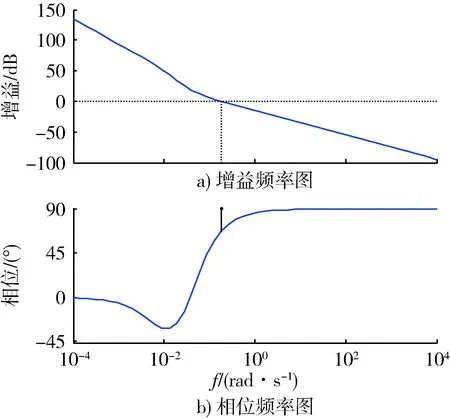
图9 风干扰到油门开环伯德图Fig.9 Bode diagram of wind to throttle

参考地速为vKc=2step(t-10)，风干扰为幅度10 m/s角频率1 rad/s的正弦信号，即vW=10sint，位置跟踪PID控制器的推力控制曲线如图10所示，速度响应和航向位置误差分别如图11和图12所示。

图10 推力控制曲线Fig.10 Curve of thrust control

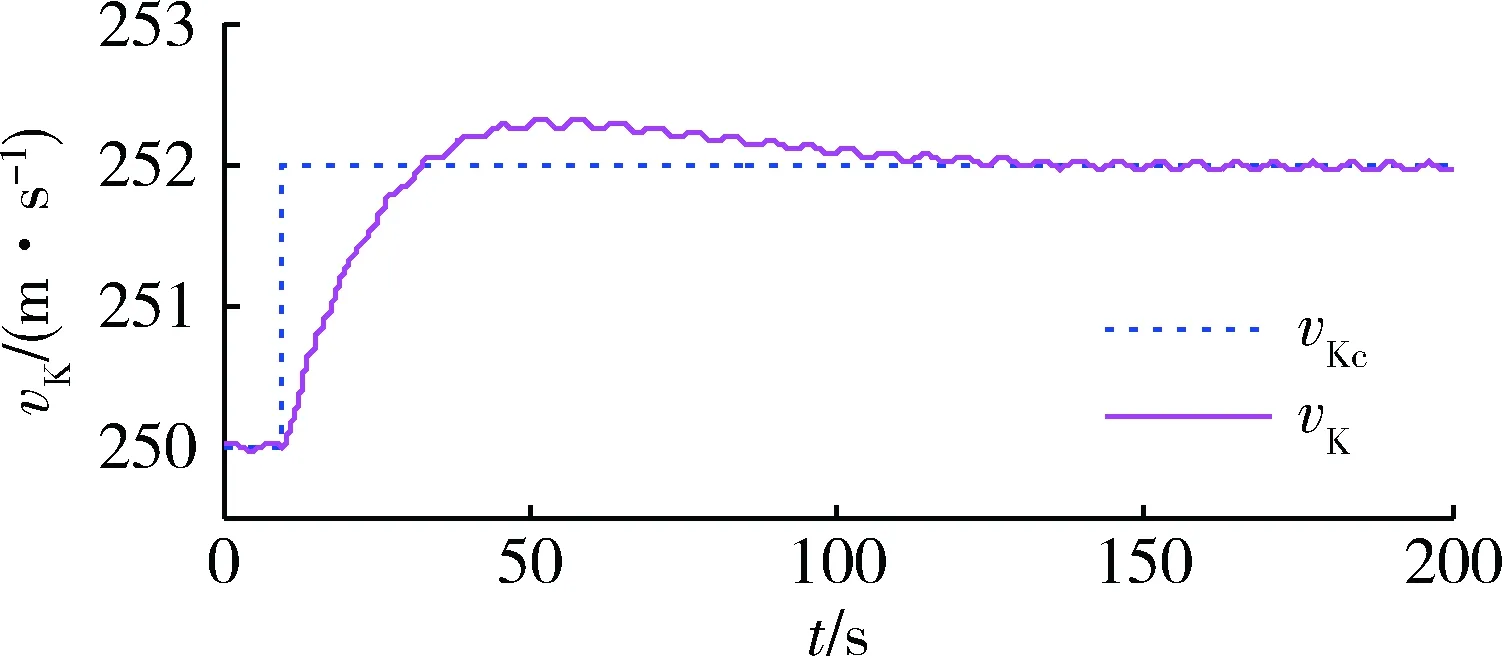
图11 地速响应曲线Fig.11 Curve of ground speed response

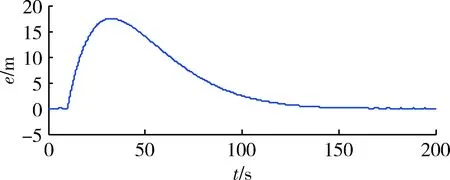
图12 航向位置跟踪误差Fig.12 Error of heading position

在t=10 s时刻，突然增加的指令速度引起推力增加，50 s后推力稳定在-6×103～8×103N之间，波动频率和干扰频率相同，抵消干扰对跟踪的影响。地速响应曲线也有小幅度的波动，且有明显的超调，地速超调是消除位置跟踪误差的必然结果，调节时间比图7中增加近一倍，地速稳态跟踪误差0.03 m/s。位置跟踪误差在t=30 s附近达到最大值17 m，t=150 s后趋于稳定，稳态跟踪误差0.05 m。

5 结束语

以组合导航系统和加速度计测量得到的飞行器运动状态作为反馈信号，将移动虚拟目标以时间为基准的航向位置、速度和加速度作为PID控制器的参考信号，按时间控制飞行器的航向位置，即可准确的控制其到达各个航路点的时刻。由于阵风干扰的存在，即使地速不变，空速也是时刻变化的，为了保证飞行稳定性和安全性，需要实时监控空速变化并防止其超出安全范围。如果只是对航路点有到达时间要求，两点间航线前半部分仍可采用空速控制模式，到达下一航路点前足够远距离处切换到地速控制模式以消除时间差。

[1] RHEE I, PARK S, RYOO C K. A Tight Path Following Algorithm of an UAS Based on PID Control[C]∥SICE Annual Conference 2010, Taipei, Taiwan: SICE, 2010: 1270-1273.

[2] 缪存孝, 房建成, 盛蔚. 一种非线性航迹自适应跟踪控制方法[J].北京航空航天大学学报, 2012, 38(4):427-431.

MIAO Cun-xiao, FANG JIAN-cheng, SHENG Wei. Adaptive Tracking Control Method for Nonlinear Trajectory [J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(4): 427-431.

[3] 李怀涛,孙静,刘大卫,等. 一种基于导航坐标系的巡飞弹航迹跟踪方法[J].弹箭与制导学报, 2016, 36(3): 15-21.

LI Huai-tao, SUN Jing, LIU Da-wei, et al. A Trajectory Tracking Approach Based on Navigation Coordinates for Loitering Munition[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2016, 36(3): 15-21.

[4] MAO Y H, CHEN Q Y, HOU Z X, et al. An Improved Nonlinear Guidance Law for Unmanned Aerial Vehicles Path Following[C]∥Proceedings of the 34th Chinese Control Conference, Piscataway, NJ:IEEE Press, 2015: 5271-5276.

[5] LI C Y, JING W X. Application of PID Controller to 2D Differential Geometric Guidance Problem[J]. Journal of Control Theory and Applications, 2007, 5(3): 285-290.

[6] 吴国强. 无人机航迹跟踪控制方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2010:24-48.

WU Guo-qiang. The Study of UAV Flight Path Tracking Control Method[D]. Harbin: Harbin Engineering University,2010:24-48.

[7] BAKER P, KAMGAR P B. Using Shorelines for Autonomous Air Vehicle Guidance[J]. Computer Vision and Image Understanding, 2010(114): 723-729.

[8] RYSDYK R. UAV Path Following for Constant Line-of-Sight[C]∥AIAA Unmanned Unlimited. Conf. and Workshop and Exhibit, San Diego, CA. September,2003:1-10.

[9] SADRAEY M. Optimal Integrated Guidance and Control Design for Line-of-Sight based Formation Flight[C]∥AIAA Guidance, Navigation, and Control Conference, Portland, Oregon, August 08-11,2011:1-14.

[10] KOTHARI M, POSTLETHWAOTE L, GU D W. UAV Path Following in Windy Urban Environments[J]. Journal of Intelligent & Robotic Systems, 2014,74(3-4): 1013-1028.

[11] 管军, 易文俊, 常思江, 等. 某型无人机三维空间航迹跟踪控制方法研究[J]. 兵工学报, 2016, 37(1): 64-70.

GUAN Jun, YI Wen-jun, CHANG Si-jiang, et al. Study of Flight Path Tracking and Control of an UAV in 3D Space [J]. Acta Armamentarii, 2016, 37(1): 64-70.

[12] SANGHYUK P, JOHN D, JONATHAN P H. Performance and Lyapunov Stability of a Nonlinear Path-Following Guidance Method[J]. Journal of Guidance, Control, Dynamics, 2007, 30(6): 1718-1728.

[13] CHO N, KIM Y. Lyapunov-Based Three-Dimensional Nonlinear Path-Following Guidance Law[C]∥AIAA Guidance, Navigation, and Control Conference,January 5-9, 2015:2366-2385.

[14] 张坤, 高晓光. 无人机三维航路自适应跟踪控制[J]. 计算机应用, 2016, 36(9):2631-2635.

ZHANG Kun, GAO Xiao-guang. Adaptive Tracking Control for Unmanned Aerial Vehicle′s Three Dimensional Trajectory[J]. Journal of Computer Applications, 2016, 36(9): 2631-2635.

[15] 鲁道夫 布罗克豪斯. 飞行控制[M]. 金长江, 译. 北京: 国防工业出版社, 1999: 152-169.

RUDOLF B. Flight Control[M]. JIN Chang-jiang, Translated. Beijing: National Defense Industry Press, 1999: 152-169.