基于DRFM的移频旁瓣干扰技术研究*

黄思源，刘东升

(军械工程学院 导弹工程系，河北 石家庄 050003)

0 引言

为区分运动和静止目标，现代雷达使用多普勒频率来提取目标的径向速度[1]，同时，各类雷达也广泛采用低旁瓣技术，以减少噪声干扰和非相参干扰对雷达正常工作的影响。传统的非相参射频存储器已经不能满足干扰多普勒雷达的要求，随着数字射频存储技术(digital radio frequency memory,DRFM)的发展，基于DRFM的干扰机由于相参复制精度极高，主要用于对脉内调制雷达以及包括脉冲多普勒雷达在内的脉间相参雷达的干扰[2]。DRFM是指使用数字电路对射频信号进行采集、存储及复制的存储技术，目前，DRFM能够将几百MHz的中频信号直接数字化并存储，在需要的时候复制出精度可达Hz量级的原始信号，并进行时延、幅度及多普勒频率等调制，重新上变频后发射给雷达，对雷达产生虚假目标或航迹。

通过DRFM干扰机形成虚假目标和航迹的实现途径主要有2种：一种是主瓣干扰方式;另一种是旁瓣干扰方式。采用单独的距离干扰或速度干扰对多普勒雷达进行欺骗容易被雷达识别，必须实施附加多普勒频率的距离-速度同步干扰措施[3]，但距离—速度同步拖引干扰都是基于主瓣干扰方式，相比之下，旁瓣干扰方式产生的虚假目标信息单一，难以达到欺骗目的。本文在基于DRFM的旁瓣干扰的基础上，结合真实目标运动特点与雷达检测多普勒频移的原理，提出移频旁瓣干扰并列举了3种干扰策略，采用Matlab软件进行了仿真验证。

1 基于DRFM的旁瓣干扰原理

1.1 DRFM干扰机工作原理

DRFM干扰机在作战中可使敌方防空雷达或导弹无法准确跟踪目标，有效掩护我方飞行器；在战术上可用于引诱敌方隐藏雷达开机，暴露其真实的兵力部署；在雷达研发上可用于测试雷达工作稳定性可靠性或模拟复杂电磁环境[4]。图1为典型DRFM工作流程图，输入的射频信号经下变频、采样、量化后以数字信号的形式被存储到高速存储器中[5]，在数字域中对距离、数量、功率等干扰信息进行调制，并由直接数字频率合成器(DDS)产生多普勒频率使信号产生频率偏移，形成速度干扰信息，信号的再生先经过数模转换，并通过相同的本振上变频，恢复到原始信号的频率。由此过程产生与雷达发射信号相参的干扰信号，能够进入发射机的频带，并实现各种欺骗干扰[6]。

图1 DRFM工作流程图Fig.1 Working flow chart of DRFM

1.2 旁瓣干扰原理

旁瓣干扰是由干扰机测出雷达的主瓣和旁瓣后，在旁瓣期间施放的干扰[7]。雷达侦查手段可使干扰机获得雷达的位置和扫描规律参数，并侦收、存储雷达的旁瓣信号，根据雷达位置和天线扫描规律、干扰机位置及预期假目标的位置信息，计算假目标到达预定位置需要的距离延时和方位延时，并对存储的雷达信号进行多普勒调制，有规律地在预定时刻将干扰信号发射出去，若信号从雷达旁瓣进入且能量大于雷达检测门限，雷达就会确认假目标的方位为当前主瓣指向的方位，从而形成预期的航迹欺骗[8]。其干扰原理如图2所示。

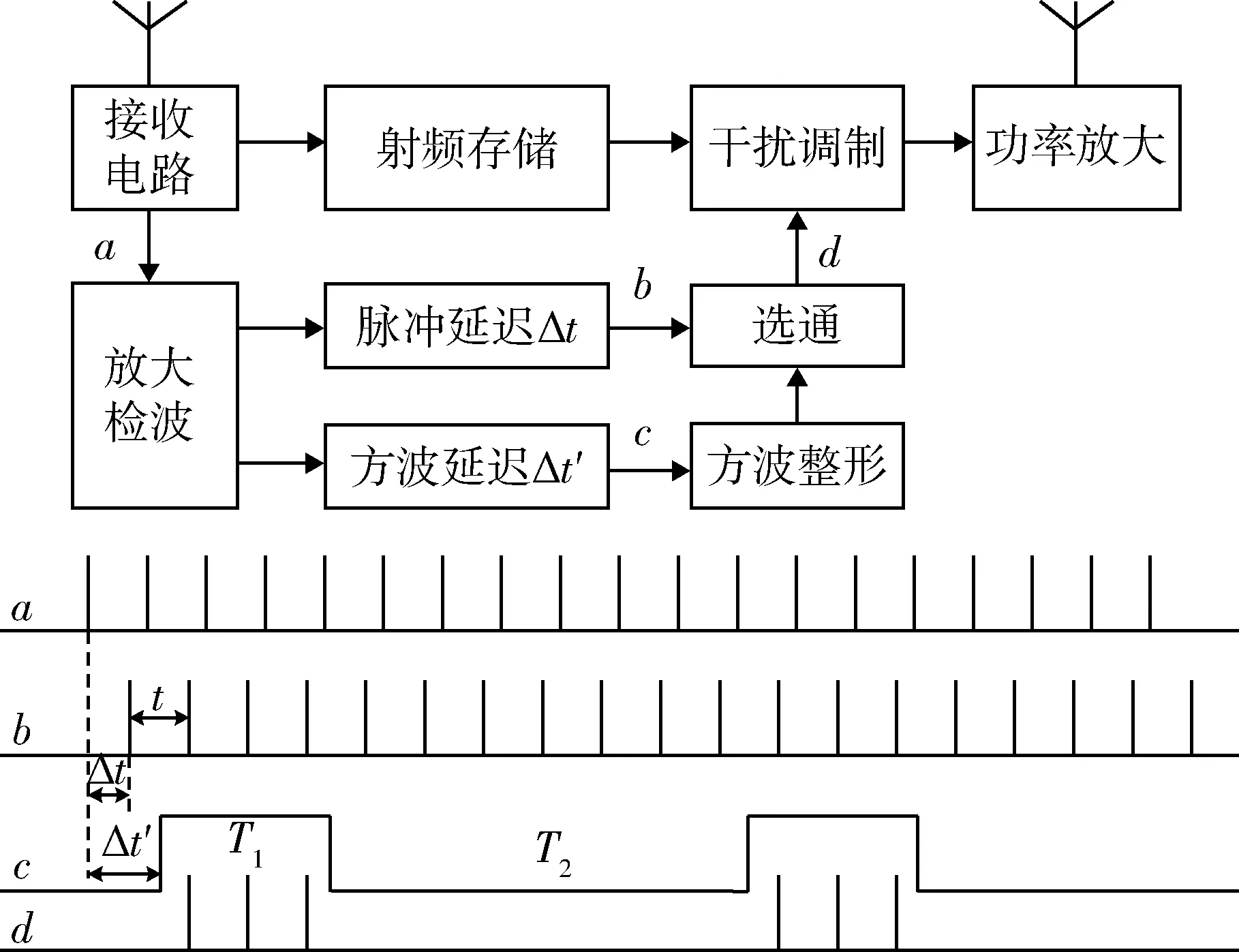
图2 DRFM旁瓣干扰原理Fig.2 Sidelobe jamming principle of DRFM

DRFM干扰机接收到雷达某旋转周期内的脉冲信号后，一路信号将射频信号以数字形式存储;另一路信号(a)经过放大检波后根据干扰策略分别进行脉冲延迟(b)和方波延迟(c)[9]。然后干扰机将信号恢复加以调制(d)：选通电路用延迟的方波选通延迟后的脉冲，将功率放大后输出，对雷达造成方位和距离同时干扰。

设DRFM干扰机的脉冲(距离)延迟时间为Δt，方波(方位)延迟时间为Δt′。T为雷达天线旋转周期，t为脉冲重复周期，T1为方波宽度，T2为收到的雷达天线主波束脉冲群信号宽度。干扰机发射一次信号产生的距离欺骗量为

R=R0+ΔR,

(1)

式中:R0为干扰机与雷达之间的距离;ΔR=c·Δt/2为雷达天线该旋转周期内的欺骗距离。

脉冲延迟时间为

Δt=2ΔR/c.

(2)

干扰机发射一次信号产生的角度欺骗量为

θ=θ0+Δθ,

(3)

式中:θ0为雷达前一旋转周期的角度总偏移量;Δθ为雷达该旋转周期的角度偏移量。干扰机转发方波延迟时间为

Δt′=Δθ/ω,

(4)

式中：ω=2π/T为天线转速。

所以，采用DRFM干扰机制定旁瓣干扰策略时需要考虑的量主要是ΔR和Δθ，而DRFM干扰机在具体实施时取决定因素的变量主要是Δt和Δt′。

1.3 干扰信号幅度调制

要对雷达形成有效的旁瓣干扰，必须满足信号能量应大于接收机灵敏度的条件[10]。与真实目标反射雷达回波的原理不同，DRFM干扰机是通过延迟转发，“主动”向雷达发射雷达波信号，其延迟时间可按干扰策略进行调整，信号功率通常大于真实目标，更容易进入雷达旁瓣。为提高干扰的逼真度和效率，干扰信号在幅度上需要符合干扰机和假目标相对雷达的位置变化规律[11]。

对一般雷达而言，发射机和接收机在同一位置，由雷达方程可得，雷达接收的目标回波信号功率为

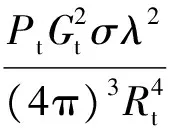
(5)

式中:Pt为雷达的发射功率;Gt为雷达天线主瓣方向的接收增益;Pt和Gt由雷达侦察设备测得;σ为目标的雷达截面积;Rt为目标与雷达之间的距离;λ为信号波长。

干扰信号到达雷达接收机是单程传输的，信号从雷达天线获得的增益随干扰信号到达方向的变化而变化[12]，雷达接收的干扰功率为

(6)

雷达接收机输入端的干扰信号功率和目标回波信号功率的比值(干信比)为

(7)

若使雷达将干扰信号识别为目标回波信号，依据功率等效控制原则，有效干扰必须满足J/S≥1，所以

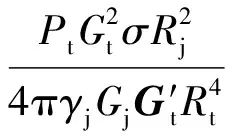
(8)

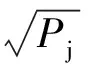
(9)

2 DRFM干扰机的多普勒移频

多普勒频移指由于目标相对辐射源的运动而引起的入射波形中心频率的偏移，速度与频移量的关系为

fd=2vrf0/c,

vr=fdc/2f0,

(10)

式中:vr为目标相对雷达径向速度;f0为雷达载波频率。

PD 雷达发射相位相参信号，采用脉冲列截取高稳定连续射频信号，根据目标相对雷达的径向速度而产生多普勒频移实现对目标测速[14]，同时对目标距离信息进行微分得到目标的速度信息。如果频移测速与微分测速的信息不匹配就会认为该目标为虚假目标并滤除。欺骗干扰PD雷达的测速功能正是利用假的多普勒频移。

多普勒假目标即对假目标信号在频域上进行移频，DRFM通过2种方式产生假多普勒频率，第1种是在重构信号上变频时采用不同的本振改变信号的载频，但这种方式产生的多普勒频率是固定值，一般用于大量假目标干扰，不适合对频移量进行精确控制[15]。本文采用第2种即正交混频的方式，通过精确控制DDS得到多普勒频率，如图3所示。

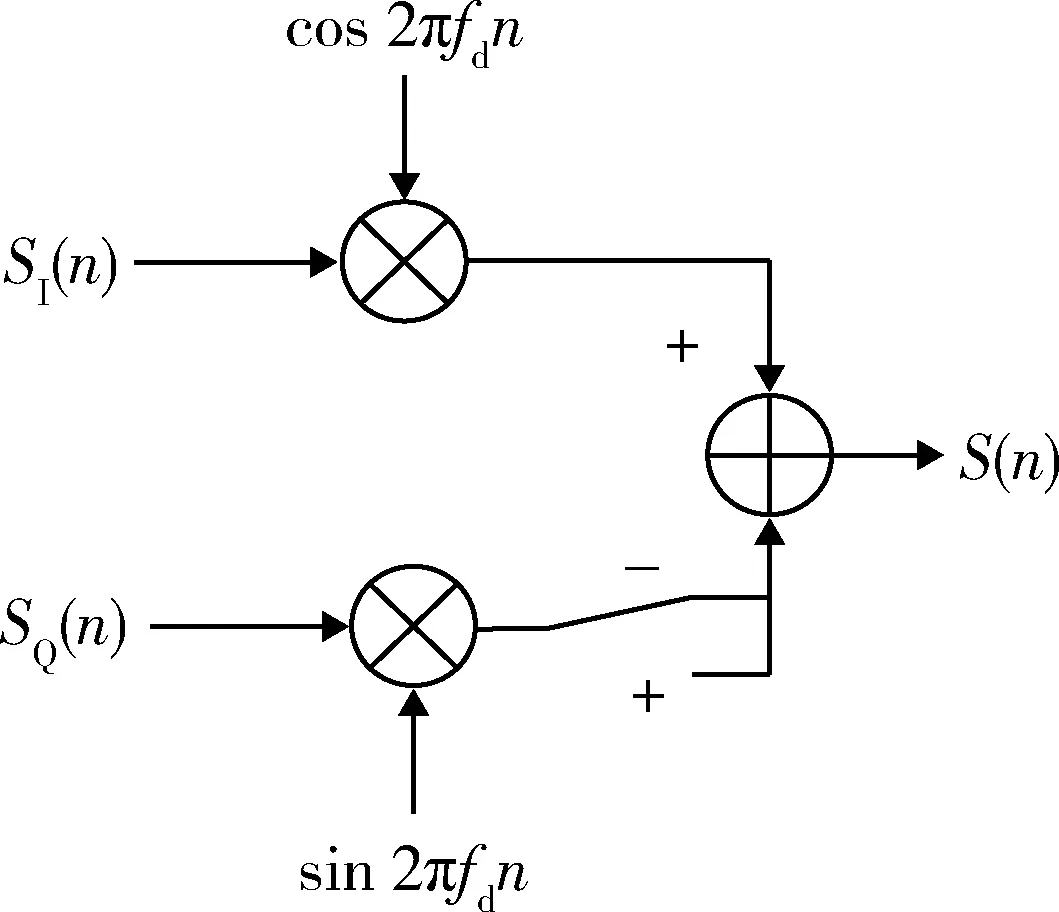
图3 正交混频方式Fig.3 Quadrature mixing mode

设DRFM接收的PD雷达信号为

S(n)=a(n)cos(2πf0+φ(n)).

(11)

经正交变换后得同相分量和正交分量分别为

SI(n)=a(n)cos(2πf0+φ(n)),

SQ(n)=a(n)sin(2πf0+φ(n)).

(12)

利用DDS产生两路信号cos 2πfdn和sin 2πfdn，分别对应乘以同相分量和正交分量，然后相减得

S(n)=SI(n)cos 2πfdn-SQ(n)sin 2πfdn=

a(n)cos[2π(f0+fd)n+φ(n)].

(13)

数字正交混频后比原信号多了一个多普勒频移分量fd。目前先进的 DDS 芯片具有高频率分辨率、低相位噪声及转换速度快等优良的性能，通过控制DDS可以合成不同的多普勒频移量，从而能形成具有不同速度不易被雷达识别的假目标。由于DDS的工作原理实际是以一个固定的钟速使相位矢量以离散的相位增量绕一个相位圆旋转的取样的数字系统，DDS产生的频率不可能瞬时变化，只能每间隔一定时间呈阶梯波变化。基于DRFM的移频技术中应用最广泛的是阶梯波移频，其原理如图4所示，DDS按照阶梯波的方式，以雷达旋转周期为间隔调整产生频率的值，然后DRFM干扰机按照设定的时延发射回波信号以达到预期的干扰效果。

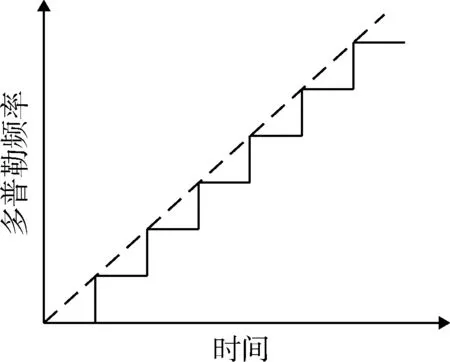
图4 阶梯波移频Fig.4 Stepped wave frequency shift

除阶梯波移频干扰外，还有线性函数移频、分段线性函数移频、随机移频[16]，修正步进移频及修正随机移频等方法[17]。这些移频方法大多基于主瓣干扰方式，可产生在雷达径向上直线运动的多假目标或造成某时间段内的覆盖干扰，缺点是移频变化的规律性比较明显，多普勒雷达可进行反向补偿来消除假目标，不适用于基于DRFM的旁瓣干扰，正因如此，旁瓣干扰的移频方法需要完善。

3 旁瓣干扰频移量计算

根据DRFM干扰机旁瓣干扰和产生多普勒频移的原理，本文提出3种旁瓣干扰策略，并附加与其匹配的多普勒频移，以提高虚假目标与真实目标的相似度，改善上述移频方法的不足。在实施旁瓣干扰时，DRFM干扰机关键的控制参数主要有脉冲延迟时间Δt、方波延迟时间Δt′和多普勒频率fd，通过推导公式可以精确计算3种旁瓣干扰策略的控制参数。

3.1 ΔR和Δθ为固定值的旁瓣干扰

雷达每旋转周期距离干扰量ΔR值和角度偏移量Δθ值固定的旁瓣干扰是最典型的旁瓣干扰样式，对DRFM干扰机而言，脉冲延迟时间Δt和方波延迟时间为Δt′都是定值，干扰控制器只需计算每个干扰点的多普勒频率fd。干扰模型如图5所示：

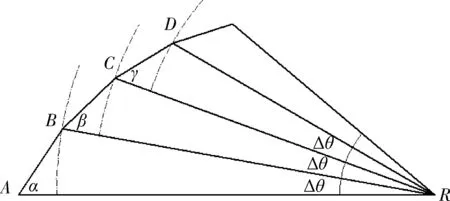
图5 第1种旁瓣干扰模型Fig.5 First sidelobe jamming model

为简化模型，设R为雷达所处位置，A为干扰机及雷达天线旋转第1个周期时假目标的位置(距离由雷达侦察设备测得)，B,C,D依次为雷达天线旋转第2，3，4个周期时的位置，满足ΔR=AR-BR=BR-CR=CR-DR，AB,BC,CD为产生的假目标之间的距离，∠α,∠β,∠γ分别为第2，3，4周时的假目标的运动方向与雷达径向的夹角，且Δθ=∠ARB=∠BRC=∠CRD，则Δt′=Δθ/ω，Δt=2·ΔR/c。

根据三角余弦定理可知，AB之间的距离为

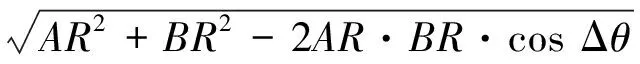
(14)

则由距离对时间的微分可知假目标在AB之间的速度为

v=AB/(T+Δt′).

(15)

假目标的速度与雷达径向夹角α为

α=arccos[(AB2+AR2-BR2)/2AB·AR].

(16)

假目标相对雷达的径向速度为

vr=vcosα.

(17)

多普勒频率计算参照式(10)。

3.2 S和Δθ为固定值的旁瓣干扰

第1种旁瓣策略方式虽然简单易实现，但产生的假目标对雷达所形成的是非匀速曲线运动，与真实的飞行器运动状态差异明显，为了产生能让PD雷达判断为匀速运动的假目标，设相邻2个假目标之间的距离为固定值S，即S=AB=BC=CD，同时将Δθ设定为固定值，则方波延迟时间Δt′和v=S/(T+Δt′)为定值，即假目标做匀速的曲线运动。脉冲延时Δt和多普勒频率fd由干扰控制器根据干扰点数反复计算得到。干扰模型如图6所示。

图6 第2种旁瓣干扰模型Fig.6 Second sidelobe jamming model

由式(14)及一元二次方程求解公式可得BR的表达式为。

(18)

则ΔR=AR-BR，脉冲延迟时间为

Δt=2ΔR/c.

(19)

易知假目标速度为

v=S/(T+Δt′),

(20)

假目标的速度与雷达径向夹角α、假目标相对雷达的径向速度vr及多普勒频率fd的计算分别参照式(16),(17),(10)。

3.3 飞行方向和S为固定值的旁瓣干扰

以上2种干扰策略形成的航迹是逐渐接近或远离雷达的曲线，无法产生直线运动的假目标，在干扰时间长、形成假目标点数多的情况下易被雷达操作员识别。第3种旁瓣干扰方式经过准确控制Δθ和ΔR，能够产生点迹为直线运动的虚假航迹。设相邻两个假目标之间的距离为固定值S，假目标运动方向始终与AR保持夹角为α1。这种旁瓣干扰方式的脉冲延迟时间Δt、方波延迟时间Δt′和多普勒频率fd均由干扰控制器根据干扰点数反复计算得到。干扰模型如图7所示。

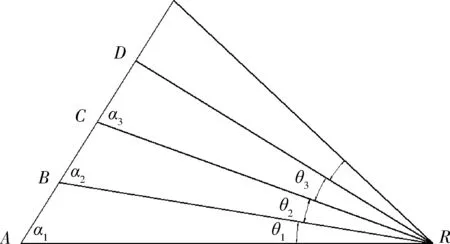
图7 第3种旁瓣干扰模型Fig.7 Third sidelobe jamming model

根据三角余弦定理可知

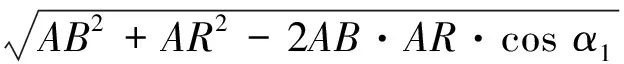
(21)

则ΔR=AR-BR，脉冲延迟时间计算与式(19)相同，假目标间夹角为

θ1=arccos[(BR2+AR2-AB2)/(2BR·AR)].

(22)

得方波延迟时间为

Δt′=∠θ1/ω.

(23)

假目标的速度为

v=AB/(T+Δt′).

(24)

假目标相对雷达的径向速度vr及多普勒频率fd的计算分别参照式(17)，(10)。

4 仿真校验及结果分析

为检验上述3种移频旁瓣干扰策略产生的假目标对雷达所形成的航迹，并精确计算DRFM干扰机产生的每个假目标应附加的多普勒频率，分别将3种干扰策略用Matlab软件进行仿真，其中，航迹仿真采用模拟雷达PPI显示屏的形式，DDS产生的多普勒频率采用阶梯波的形式。雷达和干扰机基本仿真参数设置如表1所示。

表1 仿真参数设置Table1 Simulation parameter setting

4.1 ΔR和Δθ为固定值的旁瓣干扰仿真

第1种移频旁瓣干扰的具体参数设置：每旋转周期欺骗距离ΔR=-2 km，每旋转周期欺骗角度Δθ=-2°。仿真结果如图8所示。

图8 第1种干扰模型的虚拟航迹及多普勒频率Fig.8 The false tack and Doppler frequency of first jamming model

图8a)显示，该种干扰策略能够对雷达形成连续的航迹，在雷达180°方向100 km处为第1个旋转周期内干扰机对雷达产生假目标的位置，因ΔR值为负，假目标的位置依次接近雷达，Δθ值为负使假目标向小于180°的方位运动，整个航迹是逐渐接近雷达的曲线。

由假目标点间距离对时间微分计算得速度v，进而可得雷达径向上速度分量vr的变化趋势，因fd=2vrf0/c，多普勒频率变化趋势与vr相同。图8b)显示，在本次仿真情况下，假目标应附加的多普勒频率随雷达旋转周期数的增加而逐渐降低，与典型阶梯波频移(图4所示)中频率变化的趋势明显不同，因DDS调整频率时间远远小于雷达旋转周期，该干扰方法可以完成从理论到工程实践的转变。

4.2 S和Δθ为固定值的旁瓣干扰仿真

第2种旁瓣干扰的具体参数设置：相邻2周期内假目标间的距离S=4 km，每旋转周期欺骗角度Δθ=-2°。由

(25)

知该式有2个解，取“+”或“-”均可取得假目标匀速运动的效果，在此处随机选取“+”或“-”，仿真结果如图9所示。

图9 第2种干扰模型的虚拟航迹及多普勒频率Fig.9 The false track and Doppler frequency of second jamming model

图9a)显示，该旁瓣干扰方式能够对雷达形成连续的航迹，在雷达180°方向100 km处为第1个假目标的位置，但假目标相对雷达径向距离上随式(25)选取正负号不同而表现出远离和接近，在本次仿真情况下，vr变化情况比较复杂，在取“-”时，假目标接近雷达，多普勒频率为正值，在取“+”时，假目标远离雷达，多普勒频率为负值，但是DDS无法直接合成负频率，移频方式为

S(n)=SI(n)cos 2πfdn+SQ(n)sin 2πfdn=

a(n)cos[2π(f0-fd)n+φ(n)],

(26)

即在图3中将单刀双掷开关置于“+”端，使2路数字信号相加实现频率负向移动。该干扰策略在只取“+”或“-”时，干扰效果和多普勒频率变化情况与第1种干扰策略比较接近。

4.3 飞行方向和S为固定值的旁瓣干扰仿真

第3种移频旁瓣干扰策略的具体参数设置：相邻两周期内假目标间的距离S=3.2 km，假目标运动方向与雷达180°线的夹角α=45°，仿真结果如图10所示。

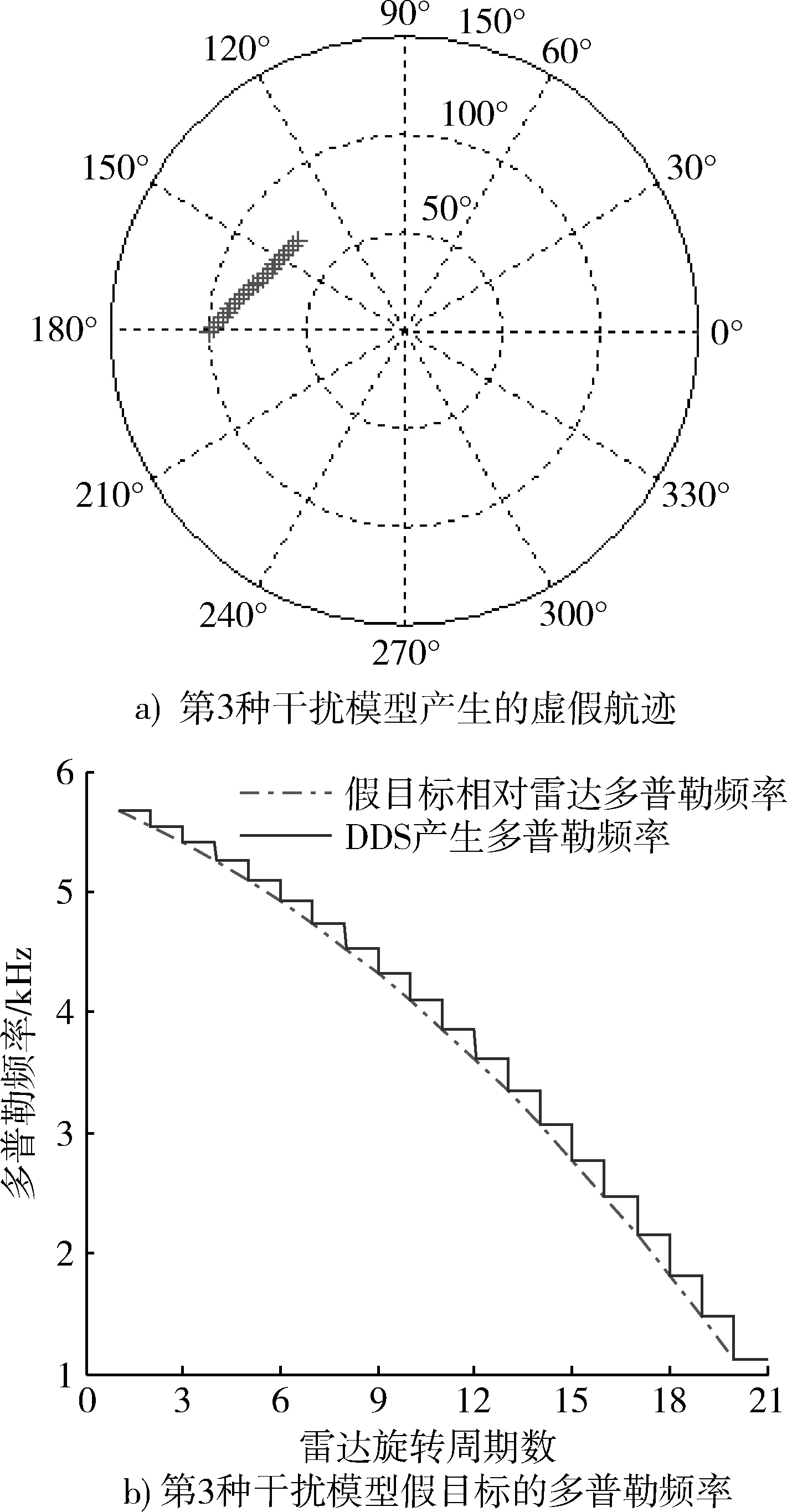
图10 第3种干扰模型的虚拟航迹及多普勒频率Fig.10 The false track and doppler frequency of trird jamming model

在本次仿真中，该旁瓣干扰策略能够对雷达形成直线运动的航迹.由于相邻2周期内雷达探测到假目标的时间间隔不等且假目标的运动方向αn=θn-1+αn-1与雷达径向的夹角在不断变化，造成假目标径向速度下降。根据变化趋势可知，若增加仿真产生的假目标次数，在假目标运动方向与雷达径向垂直时，径向速度vr和多普勒频率fd的值为0，随后vr和fd会下降为负值。

5 结束语

本文提出移频旁瓣干扰的方法并建立3种干扰模型，通过对基于DRFM的旁瓣干扰附加多普勒频率并进行幅度调制，降低雷达识别虚假目标的概率、增加雷达工作负担，以达到掩护真实目标的目的。在3种模型的基础上改变干扰的参数值会产生不同的假目标航迹，可实现精确控制的大量多普勒假目标同时干扰，仿真实验说明移频旁瓣干扰为提高雷达干扰的效率提供了一种可行方法。

[1] Bassem R Mahafza，Ater Z Elsherbeni.Matlab Simulation for Radar System Design[M].Beijing:Publishing House of Electronics Industry，2012.

[2] 唐永年.雷达对抗工程[M].北京：北京航空航天大学出版社，2012.

TANG Yong-nian.Radar Countermeasure Engineering[M].Beijing：Beihang University Press，2012.

[3] 周庆昊，严振华，冀建民，等.有源航迹假目标欺骗干扰与不明空情研究[J].舰船电子对，2013，36(3)：27-31.

ZHOU Qing-hao，YAN Zhen-hua，JI Jian-min，et al.Research into Active Track False-Target Deception Jamming and Unidentified Air Intelligence[J].Shipboard Electronic Countermeasure，2013，36(3)：27-31.

[4] 毕锐锐.宽带PD雷达回波模拟器设计与性能验证[D].北京:北京理工大学，2015.

BI Rui-rui.The Design of the Wideband PD Radar Echo Simulator and the Verification of the Performance[D].Beijing：Beijing Institute of Technology，2015.

[5] 张鹏.基于通用仪器的DRFM雷达目标模拟器实现[J].现代雷达，2015，37(8)：81-85.

ZHANG Peng.Realization of DRFM Radar Target Simulator Based on General Instruments[J].Morden Radar，2015，37(8)：81-85.

[6] 尚志刚，白渭雄，董会旭.对PD雷达进行综合欺骗干扰研究[J].火力指挥与控制，2013，38(1)：91-93.

SHANG Zhi-gang，BAI Wei-xiong，DONG Hui-xu.Investigation on Synthetical Deceiving Jamming to PD Radar[J].Fire Control & Command Control，2013，38(1)：91-93.

[7] 赵立志，魏永峰.欺骗性雷达干扰实现方法分析[J].舰船电子对抗，2013，36(4)：11-13.

ZHAO Li-zhi，WEI Yong-feng.Analysis of Implementation Method of Deception Jamming to Radars[J].Shipboard Electronic Countermeasure，2013，36(4)：11-13.

[8] 倪建春，王宝.有源欺骗干扰及雷达反对抗策略研究[J].舰船电子对抗，2011，34(3)：5-8.

NI Jian-chun，WANG Bao.Research Into the Active Deception Jamming and Radar Counter-Countermeasure[J].Shipboard Electronic Countermeasure，2011，34(3)：5-8.

[9] 韩晓东，郁文贤，舒汀，等.对线性调频信号雷达的噪声干扰方法研究[J].计算机仿真，2014，31(12)：5-8.

HAN Xiao-dong，YU Wen-xian，SHU Ting，et al.Research on Noise Jamming to LFM Signal Radar[J].Computer Simulation，2014，31(12)：5-8.

[10] 李欣，王春阳.航迹欺骗干扰及其对抗技术的研究现状与发展[J].飞航导弹，2013(8)：64-67.

LI Xin，WANG Chun-yang.Research Status and Development of Track Deception Jamming and Countermeasures[J].Aerodynamic Missile Journal，2013(8)：64-67.

[11] 柳向，王杰贵，刘兴华.对数据后处理雷达的幅度控制干扰技术研究[J].航天电子对抗，2014，30(5)：44-47，242.

LIU Xiang，WANG Jie-gui，LIU Xing-hua.Amplitude Controlling Jamming Technique Against Data Processing Radar[J].Aerospace Electronic Warfare，2014，30(5)：44-47，242.

[12] 欧阳小安.对多威胁信号的干扰功率管理技术研究[D].西安：西安电子科技大学，2013.

OUYANG Xiao-an.Study on Technology of Jamming Power Management to Multi-Threat Signal[D].Xi’an：Xidian University，2013.

[13] 宋海方，吴华，程嗣怡，等.基于射频隐身的雷达干扰功率自适应控制方法[J].火力与指挥控制，2014，39(6)：118-125.

SONG Hai-fang，WU Hua，CHENG Si-yi.Adaptive Control Method of AECM Power Based on Radio Frequency Stealth[J].Fire Control & Command Control，2014，39(6)：118-125.

[14] 甘德云，孟令智，郭慧峰.基于DRFM的距离-多普勒假目标干扰效果简析[J].航天电子对抗，2014，21(1)：25-27.

GAN De-yun，MENG Ling-zhi，GUO Hui-feng.Analysis of Jamming Effect of Range Doppler Decoy based on DRFM[J].Aerospace Electronic Warfare，2014，21(1)：25-27.

[15] 戴小军.对脉冲多普勒雷达干扰技术研究与实现[D].镇江：江苏科技大学，2013.

DAI Xiao-jun.Research and Realization of Jamming Technology Against Pulse Doppler Radar[D].Zhenjiang：Jiangsu University of Science and Technology，2013.

[16] 张克舟，李青山，张恒，等.LFM脉冲压缩雷达的随机移频多假目标干扰技术研究[J].电光与控制，2014，21(8)：106-109.

ZHANG Ke-zhou，LI Qing-shan，ZHANG Heng，et al.Randpm Frequency-Shift for Multi-False-Target Jamming of LFM Pulse Compression Radar[J].Electronics Optics & Control，2014，21(8)：106-109.

[17] 韩国强，叶瑞芳，刘 丽，等.对新型ISAR欺骗干扰效果仿真分析[J].雷达科学与技术，2014(5)：532-538.

HAN Guo-qiang，YE Rui-fang，LIU Li，et al.Simulation and Analysis of New Deception Jamming Effect on ISAR[J].Radar Science and Technology，2014(5)：532-538.