立体几何 “易错题”归类剖析

江苏省启东市汇龙中学 樊 勇

立体几何 “易错题”归类剖析

江苏省启东市汇龙中学 樊 勇

编者的话:同学们在学习的过程中,难免会出现错解的现象。本期“易错题归类剖析”栏目推出的文章,注重剖析错解原因,注重补充知识缺陷,注重题目引申变换,希望同学们认真领会,学以致用,不再发生类似的错解。

立体几何主要考查空间想象能力、推理论证能力、运算求解能力、将“空间问题平面化、模型化和代数化”的转化能力,以及一些重要的数学思想方法的应用。同学们在学习和复习中受认知水平的限制,容易进入种种思维误区,本文对立体几何的易错题归类剖析,给出提醒,希望助同学们一臂之力。

一、三视图与空间几何体体积和面积的计算

易错点1:三视图中忽视投影面和实、虚线

例1 在空间直角坐标系O-x y z中,已知A(2,0,0),B(2,2,0),C(0,2,0),D(1,1,2)。若S1,S2,S3分别是三棱锥D-A B C在坐标平面x O y,y O z,z O x上的正投影图形的面积,则( )。

错解:忽视正投影面,选A或B或C。

图1

剖析:如图1,把侧面当作正投影面,误认为S2,S3分别为△D O C,△D B C的面积。

正解:在空间直角坐标系内,作出三棱锥在三个坐标平面上的正投影,计算三角形的面积。如图1所示,△A B C为三棱锥在坐标平面x O y上的正投影,所以S=×2×2=2。1三棱锥在平面y O z上的正投影与△D E F(E,F分别是O A,B C的中点)全等,所以S2=×2×2。三棱锥在平面x O y上的正投影与△D GH(G,H 分别为A B,O C的中点)全等,所以S=×2×=。所以S=32S3且S1≠S3。故选D。

提醒:本题正投影的面积,实质就是四个顶点向坐标平面x O y,y O z,x O z上的正投影的面积,选择正确的投影面,找到正投影面上的△A B C,△D E F,△D GH进而获解。

易错点2:三棱锥体积求解中忽略等积变换

例2 如图2,在棱长为5的正方体A B C D-A1B1C1D1中,E F是棱A B上的一条线段,且E F=2,Q是A1D1的中点,P是棱C1D1上的动点,则四面体P Q E F的体积是( )。

图2

A.有最小值的一个变量

B.有最大值的一个变量

C.没有最值的一个变量

D.一个不变量

错解:选A或B或C。

剖析:忽略三棱锥体积等积变换的目标。

正解:连接Q A,则Q A为Q点到A B的距离。又因为E F=2,故S△QEF为定值。又因为C1D1∥A B,则由线面平行的判定定理易得C1D1∥面Q E F。因为P是棱C1D1上的动点,故P点到平面Q E F的距离也为定值,即四面体P Q E F的底面积和高均为定值,故四面体P Q E F的体积为定值。故选D。

提醒:对于三棱锥的体积,可任选一面作底面,目标是求出该底面面积和对应的高。

二、直线与直线、直线与平面及平面与平面的位置关系

易错点3:盲目类比平面几何中的定理和性质

例3 如图3所示,已知E,F分别是正方体A B C D-A1B1C1D1的棱A A1,C C1上的点,且A E=C1F。求证:四边形B E D1F是平行四边形。

错解:在正方体A B C D-A1B1C1D1中,平面A1A D D1∥平面B1B C C1,由两平行平面与第三平面相交得交线平行,故D1E∥F B,同理可证D1F∥E B,故四边形B E D1F为平行四边形。

剖析:错解盲目地套用平面几何定理。

正解:在△A B E和△C1D1F中,因为A B=C1D1,A E=C1F,∠E A B=∠F C1D1=9 0°,所以 R t△E A B≌R t△F C1D1,所以E B=D1F。同理可证D1E=B F。连接E F,B D1,则它们相交于各自中点,从而B,E,F,D1四点在同一平面内,所以四边形B E D1F是平行四边形。

提醒:平面几何中的有关结论在空间不一定成立,平面几何的结论在立体几何中应用遵循两点:(1)空间中放在同一平面内用;(2)先证明其在空间是真命题再用。

易错点4:忽视线线垂直和线面垂直的相互转化

图3

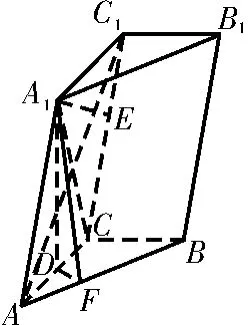
图4

例4 如图4所示,三棱柱A B C-A1B1C1中,点A1在平面A B C内的射影D在A C上,∠A C B=9 0°,A C=C C1。求证:A C1⊥A1B。

错解:由于缺少线线垂直转化为线面垂直的意识,导致思维混乱致错。

剖析:线线垂直常常构造证明一条和另一条所在的平面垂直,注意题设的特殊性,转化为A C1⊥平面C A1B。

正解:由A1D⊥平面A B C和面面垂直的判定定理知平面A A1C1C⊥平面A B C。

由题设得B C⊥A C,由面面垂直的性质定理知B C⊥平面A A1C1C,则A C1⊥B C。

连接A1C,因为A C=C C1,所以侧面A A1C1C为菱形,所以A C1⊥A1C。

故A C1⊥平面C A1B,则A C1⊥A1B。

提醒:两异面直线垂直,可以通过构建,使一条直线和另一条直线所在的面垂直,进而得到两异面直线垂直。直线与平面垂直、平面与平面垂直往往须借助直线和直线垂直加以证明。

易错点5:折叠问题中忽视折叠前后的“不变量”

例5 △A B C的边B C上的高线为A D,B D=a,C D=b,将△A B C沿A D折成大小为θ的二面角B-A D-C,若c o sθ=,则三棱锥A-B C D的侧面△A B C是( )。

图5

图6

A.锐角三角形

B.钝角三角形

C.直角三角形

D.形状与a、b的值有关的三角形

错解:选D。

剖析:将平面图形折成空间图形后线面位置关系理不清,易出错。

正解:作出平面图形(图5)和空间图形(图6),寻求折叠前后在同一平面内的图形为不变量。如图6,∠B D C=θ,c o sθ=,且B D=a,C D=b,由余弦定理知c o sθ==, 所以b2=a2+B C2,则B D⊥B C,由三垂线定理知B C⊥A B,故选C。

提醒:平面图形在折叠过程中,某些几何元素的几何量保持不变,或几何元素间的某些几何性质或位置关系不变,这些定值问题也是立体几何中的重要问题,但是我们容易忽视。翻折与展开是一个问题的两个方面,均要注意平面图形与立体图形各个对应元素的相对变化,元素间的大小与位置关系。在翻折过程中,处在同一个半平面内的元素是不变的,弄清这一点是解决这类问题的关键。

三、空间角与距离

易错点6:求点到面的距离找不到点在面上射影的位置

例6 如图7,在棱长为4的正方体A B C D-A1B1C1D1中,O是正方形A1B1C1D1的中心,点P在棱C C1上,且C C1=4C P。求点P到平面A B D1的距离。

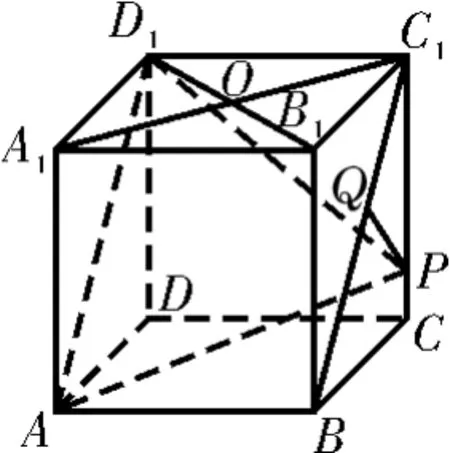
图7

错解:因为A B C DA1B1C1D1为正方体,所以A B⊥面B C C1B1,所以B P⊥A B,所以B P即为点P到平面A B D1的距离,在R t△B C P中,B P=。

剖析:线面垂直的判定有误,B P⊥A B,但B P与平面A B D1不垂直,所以点P到平面A B D1的距离不是B P。

正解:连接B C1,在平面B C C1B1中,过点P作P Q⊥B C1于点Q。因为A B⊥平面B C C1B1,P Q⊂平面B C C1B1,P Q⊥A B,P Q⊥平面A B C1D1,P Q就是点P到平面A B D1的距离,在 R t△C1P Q 中,∠C1Q P=9 0°,∠P C1Q=4 5°,P C1=3,所以P Q=,即点P到平面A B D的距离为。1

提醒:线到面、面到面的距离均可转化为点到面的距离。点到面的距离可以确定点在面上的射影直接作出来算值,也可以用向量法求解。

易错点7:混淆异面直线所成角、线面角与两向量夹角的概念

图8

例7 如图8所示,四棱锥P-A B C D中,底面四边形A B C D是正方形,侧面P D C是边长为a的正三角形,且平面P D C⊥底面A B C D,E为P C的中点。

(1)求异面直线P A与D E所成角的余弦值;

(2)求A P与平面A B C D所成角的正弦值。

错解:如图9所示,取D C的中点O,连接P O,因为△P D C为正三角形,所以P O⊥D C。又因为平面P D C⊥平面A B C D,所以P O⊥平面A B C D。

图9

剖析:(1)异面直线P A与D E所成的角和直线A P与平面A B C D所成的角均为锐角或直角,余弦值一定非负。

(责任编辑 王福华)