相位调制信号对窄线宽光纤放大器线宽特性和受激布里渊散射阈值的影响∗

刘雅坤王小林粟荣涛 马鹏飞张汉伟周朴 司磊

1)(国防科学技术大学光电科学与工程学院,长沙 410073)

2)(大功率光纤激光湖南省协同创新中心,长沙 410073)

相位调制信号对窄线宽光纤放大器线宽特性和受激布里渊散射阈值的影响∗

刘雅坤1)王小林1)2)粟荣涛1)2)†马鹏飞1)2)张汉伟1)2)周朴1)2)司磊1)2)‡

1)(国防科学技术大学光电科学与工程学院,长沙 410073)

2)(大功率光纤激光湖南省协同创新中心,长沙 410073)

光纤放大器,受激布里渊散射,窄线宽,相位调制

1 引 言

高功率窄线宽光纤激光具有转换效率高、光束质量好、热管理方便和结构紧凑等优势,在引力波探测、非线性频率转换、相干/光谱合成等领域具有重要应用[1−6].在窄线宽光纤激光中,受激布里渊散射(SBS)效应是阈值最低的非线性效应,是限制高功率窄线宽激光放大器功率提升的主要因素[7,8].国内外学者提出了多种抑制SBS效应的方法,如减小光场和声场重叠面积[9]、引入增益竞争[10,11]、降低数值孔径(NA)[12]、使用高掺杂光纤[13]与相位调制展宽种子激光光谱[14−18].其中,相位调制的方法通过展宽种子激光线宽降低布里渊增益峰值来抑制SBS,具有易操作、SBS阈值提升能力强等优势,在高功率窄线宽光纤放大器中得到广泛的运用,对相位调制抑制SBS的研究也较为深入.2012年,Zeringue等[19]建立了相位调制抑制SBS的理论模型,考虑正弦信号、白噪声信号、伪随机码信号调制后线宽与光纤长度对相位调制抑制效果的影响;次年,杜文博等[20]建立了多波长放大的传输模型,对单级正弦信号调制抑制SBS进行了理论研究;2015年,Anderson等[15]对正弦信号、白噪声信号、伪随机编码信号相位调制进行了实验研究,并与理论模型计算结果进行了对比.然而,不同相位调制手段对光谱的展宽能力及其对SBS的抑制能力尚未进行深入研究.

本文在考虑调制信号频率的同时,将调制深度作为另一变量,以调制后光谱的形态、边频间隔、谱线数目为评价项目,分析了白噪声信号(WNS)调制、伪随机编码信号(PRBS)相位调制、正弦信号相位调制三种调制手段对光谱的展宽能力.以调制后SBS阈值提升因子作为评判标准,利用基于三波耦合的含时光纤传输方程,综合考虑激光线宽、光谱形态、光声重叠因子、声子寿命、纤芯损耗等因素对Stokes光、信号光的影响,着重研究了三种调制手段对光纤中SBS效应的抑制能力.

2 理论模型

2.1 SBS三波耦合理论模型

由于实验中通常采用光纤缠绕等方法抑制光纤中高阶模的产生,获得近基模激光输出,因此采用单模近似对模型进行简化,即假定光纤中激光与布里渊Stokes光均以基模形式传输.单模情况下,

可以假定光场的横向分布近似均匀,即不考虑增益的横向局部饱和效应,因此在包含SBS效应的单频光纤放大器理论基础上,结合光纤放大器的速率方程,考虑Stokes光对反转粒子数的消耗,可得到速率方程:

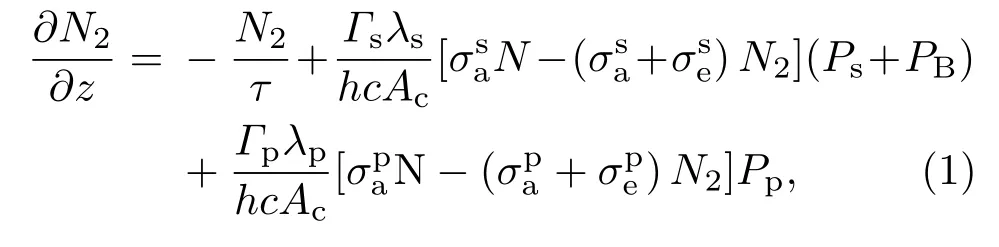
式中P为功率,Γ为重叠因子,上标和下标p,s,B分别表示抽运光、信号光和Stokes光,σa,σe分别表示吸收与发射截面,N为有效掺杂浓度(假设N沿光纤均匀分布),N2为上能级粒子数,Ac为纤芯截面积,h为普朗克常数,c为光速,τ为镱离子上能级平均寿命.根据(1)式,可由增益光纤上任意一点的激光强度来计算该处粒子数反转分布状态,从而可得抽运光功率传输方程,即

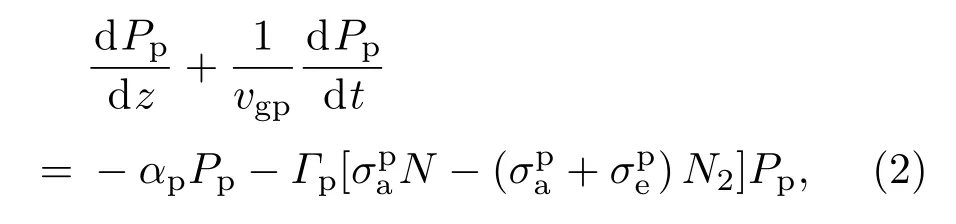
式中αp为光纤损耗系数,νgp为抽运光的群速度.根据三波耦合原理[21−23],结合速率方程及光纤中声波场的分布,考虑信号光与Stokes光的自相位调制与交叉相位调制以及噪声项等因素对激光传输的影响,信号光、Stokes光和声波场的归一化振幅As,AB与Q满足如下方程:

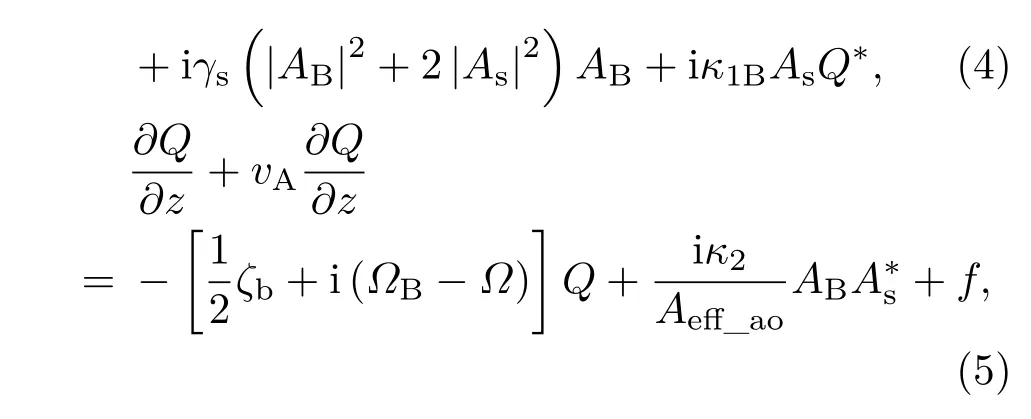
式中As为信号光归一化振幅,ΩB为声波频率,Ω为可取频率值,vA为声速,ζb为声阻尼率,Aeff_ao为声光有效作用面积,κ1s,κ1B和κ2为耦合系数,αs为信号光损耗系数,γs为非线性系数.f为自发引起SBS的热噪声源,f满足以下关系:

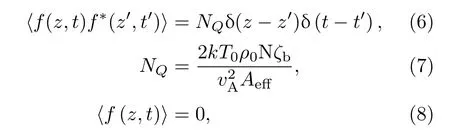
式中k为玻尔兹曼常数,T0为温度,ρ0为光纤密度,Aeff为光纤有效模场面积.

2.2 相位调制信号模型

相位调制使信号光沿中心频率产生一定的边频,将能量分布到大量光载波上,降低光功率谱能量密度,当展宽后光谱间隔小于布里渊增益带宽时,不同边频产生的布里渊增益谱互相叠加,使后向Stokes光减弱,提高系统SBS阈值[24−27].实验中常用的信号为正弦信号、白噪声信号和伪随机二维码序列信号.

正弦信号是最早在实验中使用的相位调制信号,用EM0和νm1分别表示相位调制信号的振幅与频率,则采用的正弦调制信号可定义为

式中EM0= πδ1Vπ/2,δ1为调制幅度,Vπ/2为调制器半波电压;ν0为调制频率.调制深度dM为调制幅度δ1与π的乘积,所用调制频率为0.2 GHz的单级正弦调制信号的时域频域如图1所示.

白噪声信号是实验中常用的一种噪声源,其幅度、功率谱密度均服从高斯分布[28],

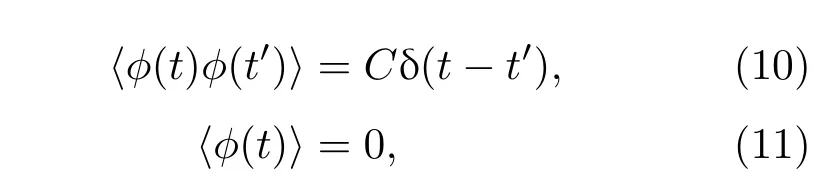
式中C为常数,0＜ϕ(t)≤dM.此时,调制频率ν0为调制信号的截止频率.图2所示为本次计算中应用的0.1 GHz白噪声调制归一化时域频域图.

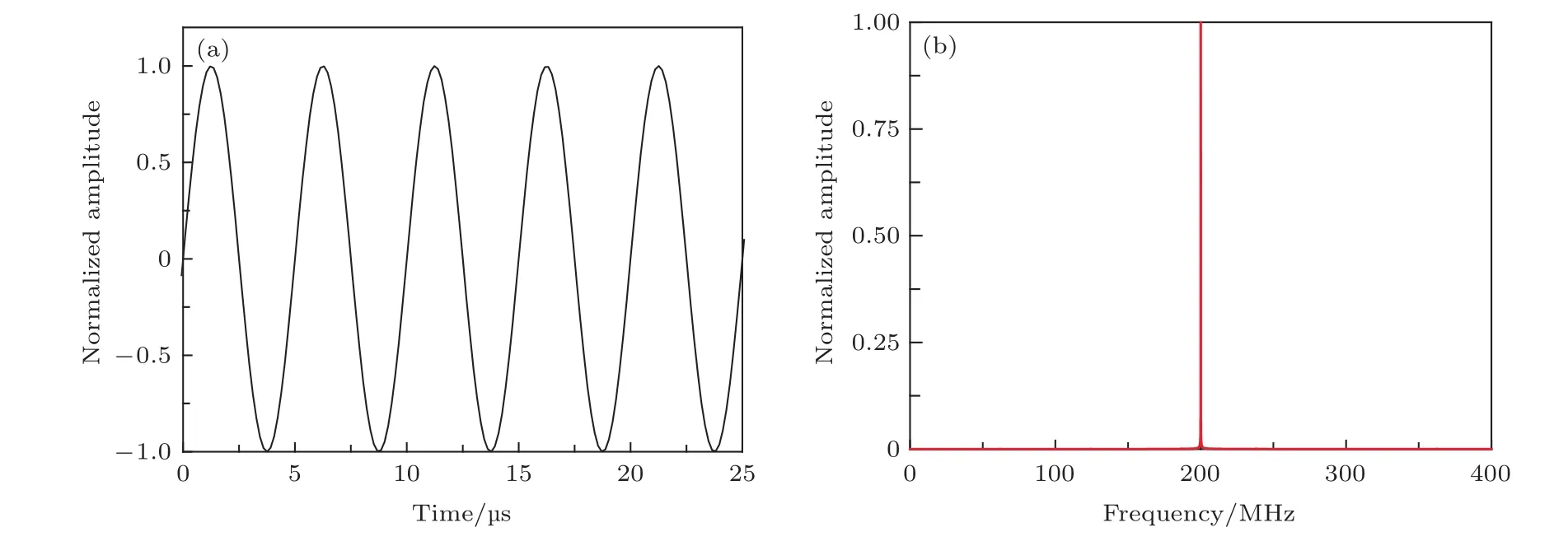
图1 正弦调制信号的(a)时域图和(b)频域图Fig.1.Sinusoidal signal in(a)time domain and(b)frequency domain.

图2 白噪声信号的(a)时域图和(b)频域图Fig.2.White noise signal in(a)time domain and(b)frequency domain.

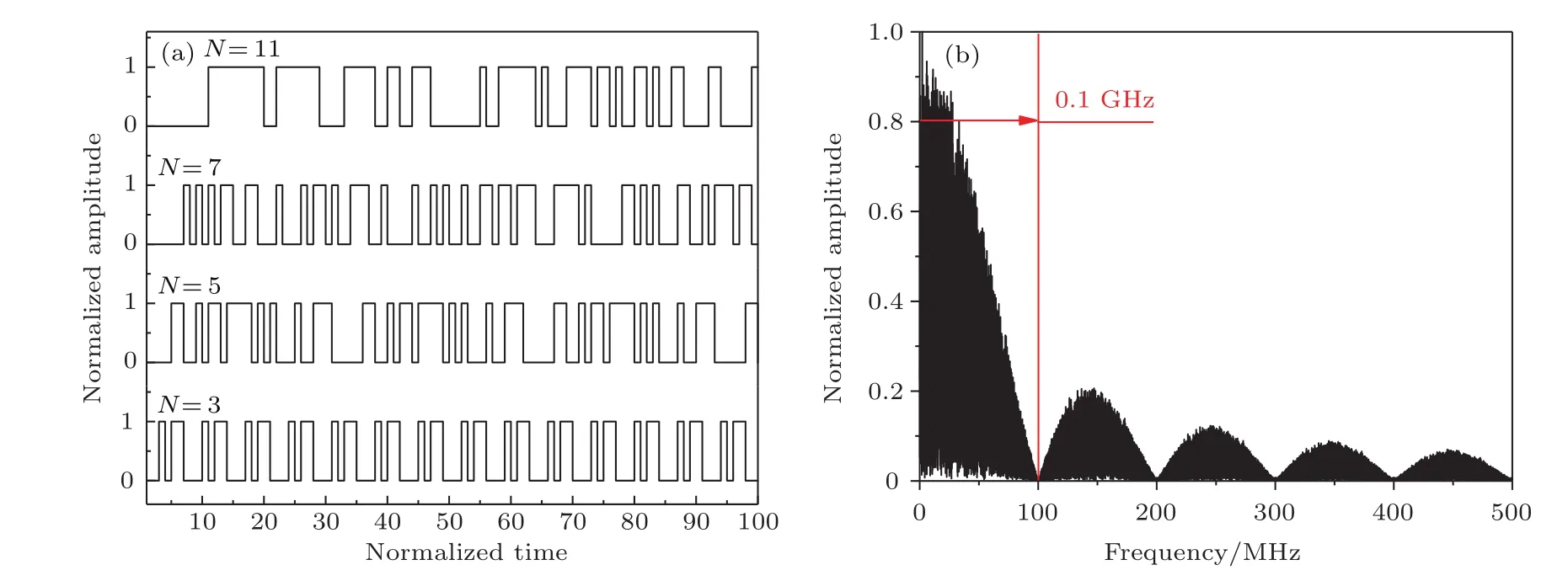
图3 (a)PRBS时域图;(b)N=7,ν0=0.1 GHz,dM=π时的PRBS频域图Fig.3.(a)PRBS in time domain;(b)PRBS in frequency domain when N=7,ν0=0.1 GHz and dM= π.

伪随机编码信号采用如下定义:N位伪随机码由移位寄存器网络产生2N−1个码长为N的“0”“1”数列构成.应用在相位调制中,当附加调制深度为“1”时,相移为π,N位PRBS调制码表达式为

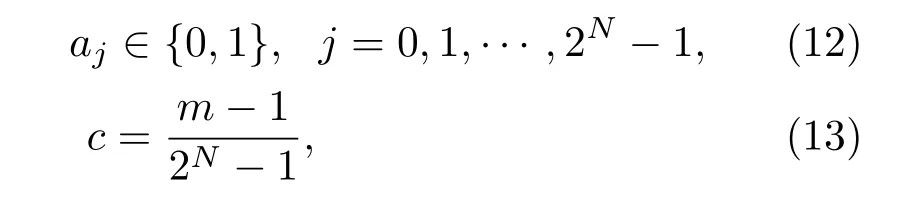
式中c为占空比;m表示该序列中“1”的个数,实际应用中,常用的伪随机码为M序列,以7位伪随机码为例,可通过x6+x7+1产生.不同N值的伪随机编码信号时域图如图3(a)所示,随着N的增大,输出调制信号的无序性逐渐提高,连续高/低电平的持续时间Δt增加.图3(b)所示为0.5 GHz,N=7时的调制信号频域图.与白噪声信号不同,PRBS在频域为精细分立信号,呈近sinc2型分布.调制频率为调制信号的时钟频率,在频率范围内表现为主峰截止频率,调制深度通常采取π的整数倍表示.

3 数值仿真及分析

计算中信号光波长设置为λs=1064.0 nm,取布里渊频移16 GHz[29],并保留5位有效数字,可得Stokes波长λB=1064.1 nm.仿真假设掺镱光纤长度为9 m,纤芯/内包层直径为20/400µm,掺镱光纤后连接3 m被动光纤,抽运激光波长为976 nm,单频信号光功率为18 W,其他物理量及物理意义如表1所示[30].考虑到相位调制后信号光频率间隔较小,因此忽略调制后的边频在波长、吸收截面、发射截面、重叠因子和背景损耗等方面的差别,在计算中将它们的布里渊散射光近似等效.

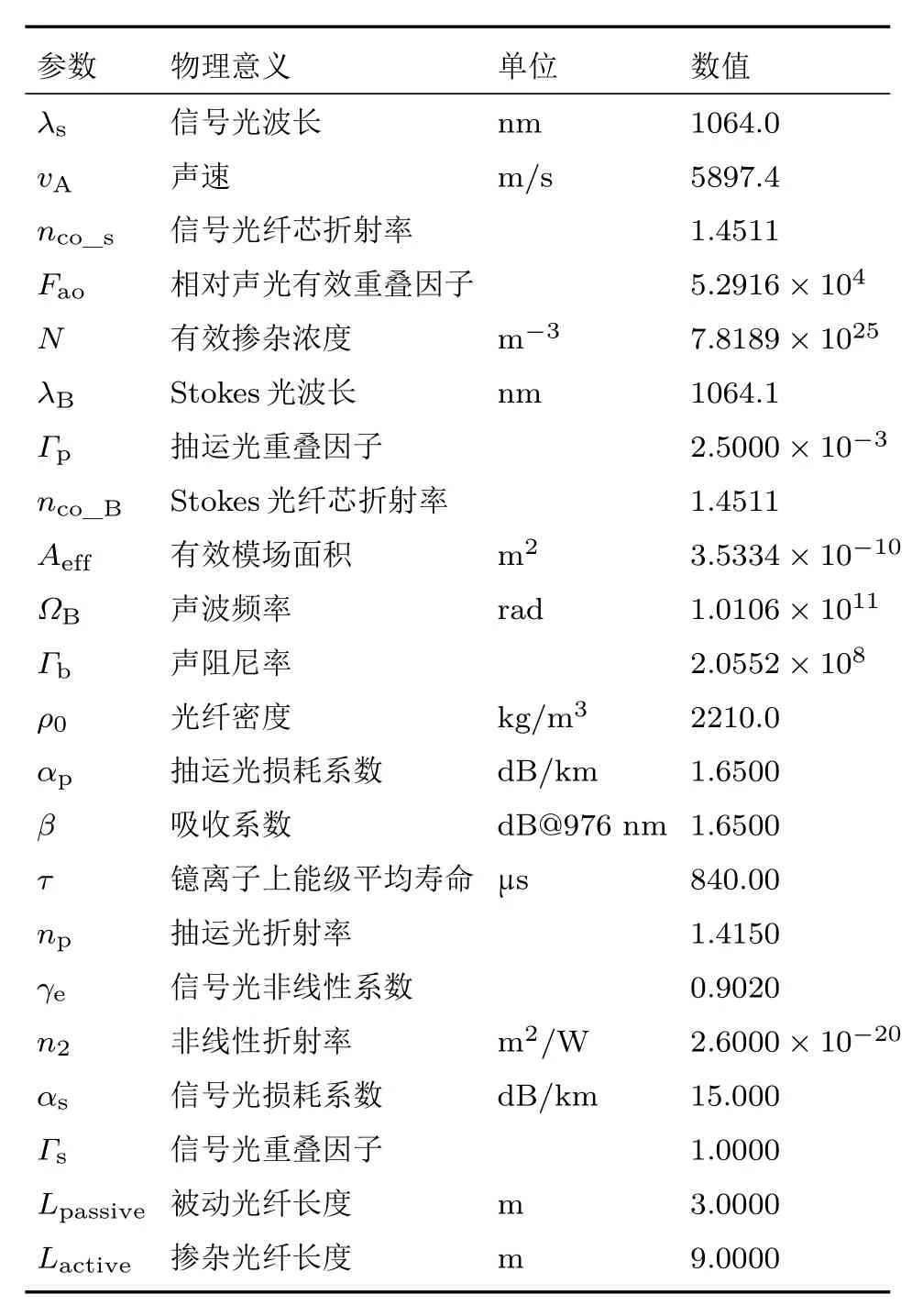
表1 主要参数及其物理意义Table 1.Main parameters and their physical meanings.

采用并行双向的有限时域差分算法[31]求解(1)—(8)式.通过计算光纤中光场轴向分布随时间的推演值,求取稳态时光纤中抽运光、信号光与Stokes光的分布.不断增加抽运功率,直至后向Stokes回光功率与输出激光功率的比值(回光比RR)大于2×10−4,定义此时的输出功率为系统SBS阈值(TSBS).对于严格单频信号光,TSBS=43 W.使用SBS阈值增强因子(FSBSE)来表征SBS阈值提升倍数,FSBSE定义为调制后的SBS阈值与单频情况下的SBS阈值之比.

3.1 正弦信号调制

首先研究利用(8)式所示正弦信号进行相位调制时系统的SBS抑制能力.激光线宽定义为幅值大于最高幅值1/e时的谱线宽度.如图4所示,单频激光经正弦信号调制后输出多边频激光.比较图4(a)与图4(b)可知,随着调制深度的增加,谱线数目、谱线间隔及线宽也会增加;比较图4(a)与图4(c)可知,随着调制频率的增加,谱线数目不再增加,但谱线间隔与线宽逐渐增加.可知谱线数目由调制深度决定,而各相邻边频间频率间隔由调制频率与调制深度共同决定.因此考虑采用级联正弦信号调制产生的光谱线填充单级正弦信号调制的谱线间隙,如图4(d)所示,在调制后种子线宽一定时,级联正弦信号调制可显著增加调制后的谱线数目,减小谱线间隔.

图5表明经正弦信号相位调制后,尽管线宽随调制频率增大而线性增加,SBS阈值随调制频率呈近对数函数增长,调制频率小于30 MHz时,FSBSE增长速度最大,调制频率大于30 MHz后,FSBSE增长速度逐渐减慢,调制频率约为100 MHz时FSBSE增长速度最小.这是由于调制后边频间隔小于二倍布里渊增益带宽,由各边频产生的Stokes光相互叠加,有效抑制了光纤中的SBS效应.随着调制频率的不断增大,谱线间隔也逐渐增加,由各边频产生的Stokes光重叠面积逐渐减小,因而FSBSE的增长速度变小.当调制频率继续增加时,各边频产生的Stokes光相互独立,不再重叠,系统SBS阈值仅由单一谱线的最高功率决定.由于计算使用的掺镱光纤布里渊增益带宽约为30 MHz,因而调制频率大于30 MHz时,系统SBS阈值随着调制频率的增加增长速度迅速下降.此外,增加系统调制深度,SBS阈值也会随之增加,这是由于随着调制深度的增加,谱线数目越多,能量分布越均匀,功率谱密度越低,则系统SBS阈值越高.

单级正弦信号调制可产生的谱线数目较少,单一谱线对功率的分担能力有限,因而采用级联正弦信号调制来填补单级正弦信号调制较宽的谱线间隙,可有效提高系统SBS阈值.如图6所示,相较于单级正弦信号相位调制,级联正弦信号相位调制在得到相同线宽的情况下FSBSE更高,是一种更为有效的调制手段.

图4 (a)ν0=0.1 MHz,dM=0.8π,(b)ν0=0.1 MHz,dM=2.8π,(c)ν0=0.4 MHz,dM=0.8π时单级正弦信号调制的种子频谱;(d)级联正弦信号调制的种子频谱Fig.4.Frequency spectra of single sinusoidal modulated seed when(a)ν0=0.1 MHz,dM=0.8π,(b)ν0=0.1 MHz,dM=0.8π,(c) ν0=0.4 MHz,dM=4.8π;(d)frequency spectra of cascade sinusoidal modulated seed.

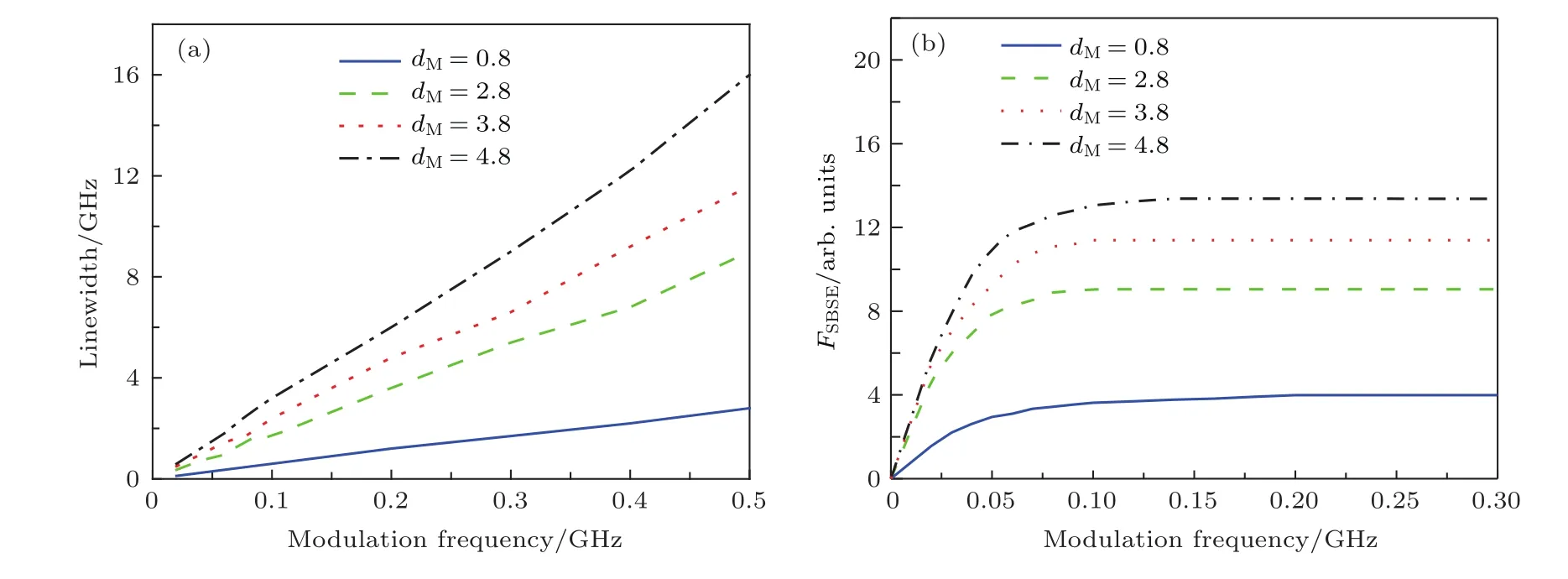
图5 不同调制深度下(a)线宽和(b)FSBSE与调制频率的关系Fig.5.(a)Modulated seed linewidth versus modulation frequency and(b)FSBSEversus modulation frequency for different modulation depths.

图6 单级正弦信号调制和级联正弦信号调制条件下线宽与FSBSE的关系Fig.6.FSBSEversus linewidth for single sinusoidal modulation and cascade sinusoidal modulation.

3.2 白噪声信号调制

实验中常用的白噪声调制系统结构可参见文献[22],白噪声调制信号由带通滤波器滤波,并经由射频(RF)放大器放大后驱动电光调制晶体,从而改变种子光的相位.单频信号经白噪声信号调制后谱线为近高斯型,如图7所示.分别比较图7(a)与图7(b)、图7(c)可知,调制频率与调制深度共同作用于调制线宽,呈正相关关系.由图7(d)可知,当调制深度较小时,调制后种子边频成分幅值显著低于主频,谱线接近于单频信号.

如图8(a)所示,对单频信号进行多次调制,得到的调制信号线宽接近,且平均值与调制频率成正比.由图8(b)可知,FSBSE随着调制频率的增加逐渐提高,呈近线性关系,同时FSBSE随调制深度的增加而增加,这是由于调制频率和调制深度的增加使得调制后光谱的线宽展宽.

图9分析了调制深度与系统FSBSE和调制后种子线宽之间的关系.由图易知,二者增长趋势基本相同,调制深度通过改变种子线宽影响系统SBS阈值.根据SBS阈值的提升情况,可以将调制深度分为三个区域,即启动区(0＜dM≤6)、线性区(6＜dM≤31)和饱和区(dM＞31).在线性区内,SBS阈值与线宽、调制深度呈近线性关系;在饱和区内,继续增加调制深度无法进一步增大种子线宽,因此阈值增长逐渐趋于平缓;而在启动区,随着调制深度逐渐减小,调制谱线宽度迅速趋于0,阈值也接近单频阈值.

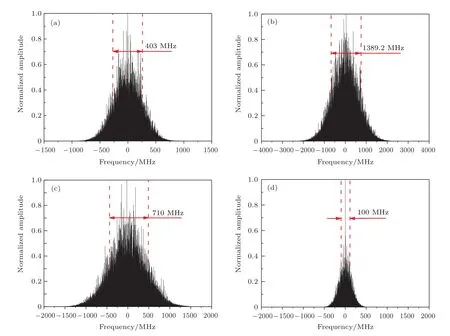
图7 不同调制频率与调制深度下的种子频谱 (a)ν0=0.1 GHz,dM=20;(b)ν0=0.3 GHz,dM=20;(c)ν0=0.1 GHz,dM=32;(d) ν0=0.1 GHz,dM=12Fig.7.Frequency spectra of the WNS modulated seed for different modulation frequencies and different modulation depths:(a)ν0=0.1 GHz,dM=20;(b)ν0=0.3 GHz,dM=20;(c)ν0=0.1 GHz,dM=32;(d)ν0=0.1 GHz,dM=12.

图8 调制频率与(a)线宽和(b)FSBSE的关系Fig.8.(a)Linewidth and(b)FSBSEas a function of modulation frequency.

图9 调制频率为0.3 GHz时调制深度与FSBSE及线宽的关系Fig.9.FSBSEand linewidth as a function of modulation depth when modulation frequency is 0.3 GHz.

3.3 伪随机编码信号调制

经PRBS调制的单频激光光谱为近sinc2型精细结构的分立光谱,谱线形态仅取决于调制频率与调制信号的编码方式.由图10可知调制后线宽约等于调制频率,且N值越大,谱线密度越大.PRBS调制方式下的光谱线数目仅与码长N有关,随着N的增加,光谱线数目不断增加.

与正弦信号、WNS调制方式不同,PRBS调制对SBS的抑制能力与码长有关.比较分析了码长为3,5,7,11时不同频率调制信号对SBS的抑制能力.由第2节分析可知,在谱线数目一定时,系统对SBS的抑制能力存在最大值,如图11中ν0=1.3 GHz,N=3处,单纯提高调制频率并不能提高系统SBS阈值,此时调制信号产生的边频间隔大于二倍布里渊频移,影响SBS阈值的因素为最大边频功率.

值得注意的是,当调制信号输出低电平时,由电光调制器加在信号光上的相移为0,结合图3与第2节分析可知,随着N的增加,连续高/低电平的持续时间Δt延长.当这一时间窗口大于镱离子上能级粒子寿命时,高功率信号光将在系统中激发SBS效应,降低系统阈值.N=11,ν0＜1.3 GHz时,Δt远大于光纤中的声子寿命与激光在9 m光纤中的往返传输时间,因而SBS阈值远小于码长较短的N=5的PRBS[19].与其他信号相比,N=7,0.7 GHz＜ν0＜2 GHz时,调制信号低电平持续时间远小于声子寿命,由高电平引入的相移π有效阻止SBS效应的产生,提高系统阈值.

由图12可知,PRBS调制方式下FSBSE随调制深度变化较大,呈近正弦函数线型分布,微弱的深度偏移便会导致FSBSE迅速降低.这是由于在调制深度偏移π后,调制谱线迅速接近单频,因而阈值迅速降低.其中,dM=0.96π时FSBSE略大于dM=π(半波电压)时,这是由于适当减弱调制可在一定程度上改善光谱线的平整度(3×10−4)[32].因此,在π附近调节调制深度,可获得更好的调制效果.

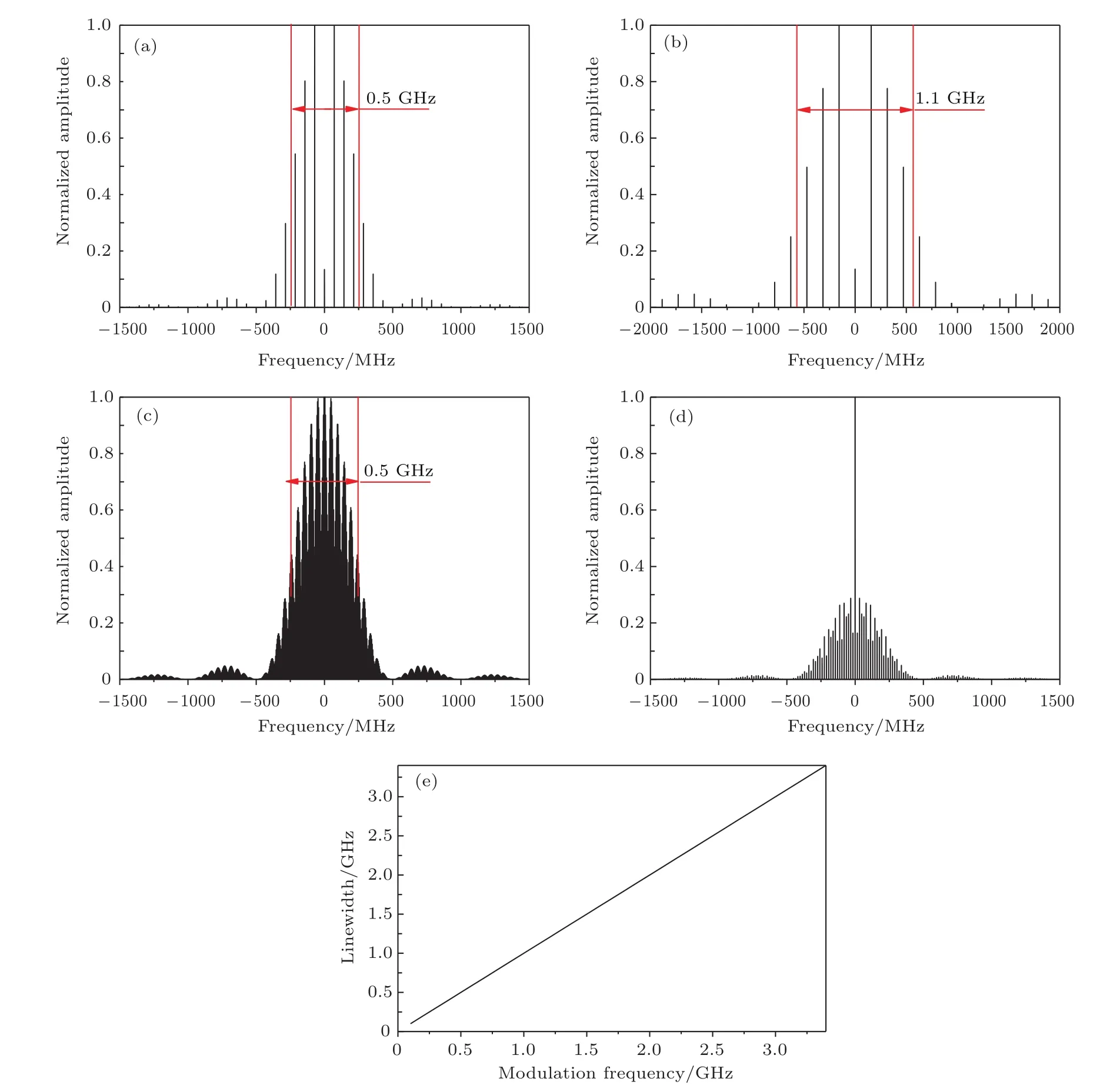
图10 (a)ν0=0.5 GHz,dM= π,N=3,(b)ν0=1.1 GHz,dM= π,N=3,(c)ν0=0.5 GHz,dM= π,N=7,(d)ν0=0.5 GHz,dM=0.85π,N=7时的种子频谱;(e)dM=π,N=7时线宽与调制频率的关系Fig.10.Frequency spectra of the PRBS modulated seed when(a)ν0=0.5 GHz,dM= π,N=3,(b)ν0=1.1 GHz,dM= π,N=3,(c)ν0=0.5 GHz,dM= π,N=7,and(d)ν0=0.5 GHz,dM=0.85π,N=7;(e)linewidth versus modulation frequency when dM=π,N=7.

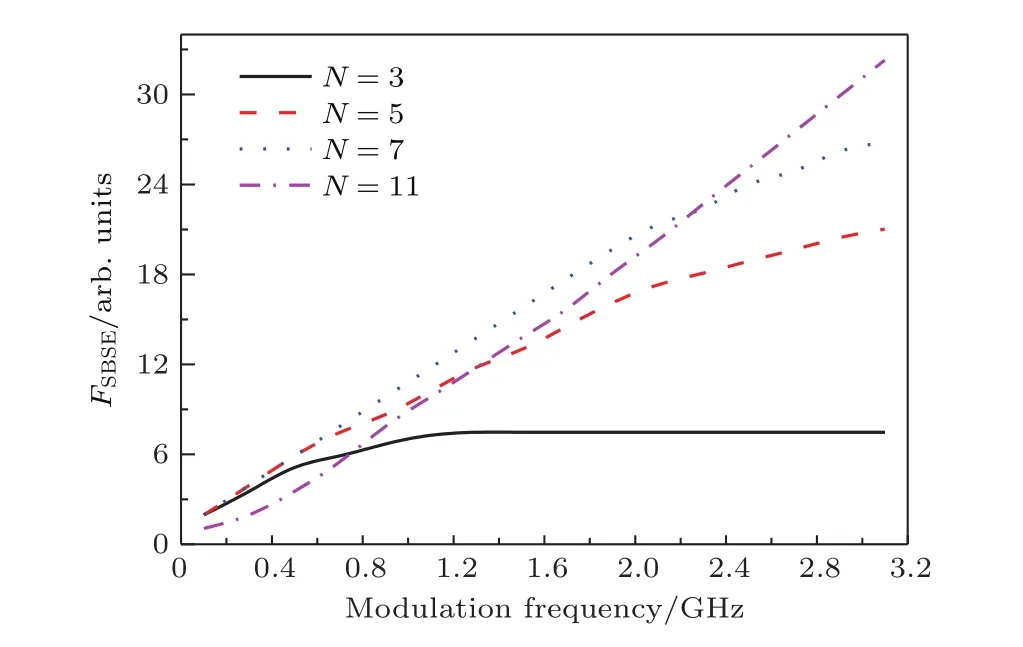
图11 (网刊彩色)调制频率与FSBSE的关系Fig.11.(color online)FSBSEversus modulation frequency.

图12 ν0=0.5 GHz,N=7时PRBS调制方式下调制深度对FSBSE的影响Fig.12.Normalized FSBSEas a function of modulation depth when the seed is modulated by PRBS with ν0=0.5 GHz and N=7.

3.4 对比分析

通过控制调制信号的类型、频率和调制深度,可以改变调制后激光光谱的谱线间隔、谱线数目与光谱平整度,从而影响光谱线宽与放大器的SBS阈值(表2).其中,正弦信号调制的谱线数目、谱线间隔分别与调制深度、调制频率呈正相关关系.在调制深度一定且调制频率低于30 MHz时,调制后种子线宽与SBS阈值随调制频率的增加呈线性变化.当调制频率大于30 MHz且小于100 MHz时,SBS阈值增长速度逐渐减小.当调制频率高于100 MHz时,尽管种子线宽随调制频率的增加逐渐增大,但进一步提升SBS抑制能力需通过提高调制信号的调制深度增加光谱线数目来实现.WNS调制后的激光光谱为密集高斯型光谱,调制频率与调制深度能够改变谱线数目与谱线间隔.调制后的激光线宽随调制频率增大线性增加,随调制深度增大呈S型增加,因而SBS阈值也随之呈线性和S型增加.PRBS调制后的激光光谱为分立的近sinc2型光谱线,谱线数目与调制信号码长呈正相关,谱线间隔与调制频率和码长呈负相关.在低调制频率的光纤放大器中码数较低的PRBS对SBS抑制能力更强,反之亦然.

综合以上分析,采用正弦信号调制时,将调制频率设置为100 MHz左右并增大调制深度或进行级联正弦信号相位调制,可获取最佳SBS抑制效果.在白噪声调制方式下,为了得到最佳SBS抑制效果,可使系统工作在线性区或饱和区.值得注意的是,由于种子经白噪声调制后线宽远大于调制频率,在实际使用中应根据线宽与输出功率需求选择合适的调制频率与调制深度.对于PRBS调制方式,由于SBS的抑制效果与码长N紧密相关,在调制频率较低的光纤放大器中,应优先采用码数较低的PRBS.应用于调制频率较高的光纤放大器中时,应增大PRBS的N值.在常用的1—2 GHz区间内,N=7时系统对SBS效应的抑制能力最优.此外,为了获得理想的SBS抑制效果,需要将PRBS的调制深度控制在π附近.通过图5、图8和图11综合比较三种调制信号调制后种子线宽与相应FSBSE,不难发现获得相同的线宽时,经正弦信号、WNS,PRBS调制的系统SBS阈值逐渐提高.因此,PRBS调制是相对更为优越的一种调制手段.

4 结 论

本文基于三波耦合的含时光纤传输方程,综合考虑激光线宽、光声重叠因子、声子寿命、纤芯损耗等因素对Stokes光、信号光的影响,对相位调制的窄线宽光纤放大器进行了理论研究,讨论了正弦信号调制、白噪声信号相位调制、伪随机编码信号调制的不同参数对调制后种子线宽的影响与光纤中SBS效应的抑制效果.

研究发现,在布里渊增益带宽约为30 MHz时，100 MHz附近为单级正弦的最佳调制频率.此外,增加调制深度或采用级联相位调制为提高正弦调制的SBS抑制能力的有效方法.对于白噪声信号调制,增加调制深度与调制频率均可提高SBS阈值,但由于调制后种子线宽较大,应根据实际需求调节调制深度与调制频率.PRBS对SBS的抑制效果与码长紧密相关,在调制频率较低的光纤放大器中,应优先采用码数较低的PRBS.此外,为了获得理想的SBS抑制效果,需要控制PRBS的调制深度约为π.种子光经过调制得到相同线宽时,由PRBS驱动的相位调制方法对SBS的抑制能力更强.

[1]Richardson D J,Nilsson J,Clarkson W A 2010J.Opt.Soc.Am.B27 11

[2]Andrés M V,Cruz J L,Díez A,Pérez M P,Delgado P M 2008Laser Phys.Lett.5 2

[3]Bufetov I A,Dianov E M 2009Laser Phys.Lett.6 6

[4]Kobyakov A,Sauer M,Chowdhury D 2010Adv.Opt.Photonics2 1

[5]Wei S Y,Jin D C,Sun R Y,Cao Y,Hou Y B,Wang J,Liu J,Wang P 2016Chin.J.Lasers43 0402005(in Chinese)[魏守宇,金东臣,孙若愚,曹镱,侯玉斌,王静,刘江,王璞2016中国激光43 0402005]

[6]Bowers M S 2015SPIE Defense+Security,Maryland,United States,April 20–24,2015 p0J

[7]Ran Y,Tao R M,Ma P F,Wang X L,Su R T,Zhou P,Si L 2015Appl.Opt.54 24

[8]Liao S Y,Gong M L 2007Laser Optoelectron.Prog.44 6(in Chinese)[廖素英,巩马理 2007激光与光电子学进展44 6]

[9]Gray S 2006In Optical Amplifiers and Their ApplicationsWhistler,Canada,June 25,2006 pOSuB1

[10]Naderi N A,Flores A,Anderson B M,Dajani I 2016Opt.Lett.41 17

[11]Flores A,Dajani I 2014Conference on Lasers and Electro-OpticsCalifornia,United States,June 813,2014 p1

[12]Beier F,Hupel C,Nold J,Kuhn S,Hein S,Ihring J,Sattler B,Haarlammert N,Schreiber T,Eberhardt R,Tünnermann A 2016Opt.Express24 6011

[13]Yu C X,Shatrovoy O,Fan T Y 2016SPIE LASE,San Francisco,United States,March 9,2016 p972806

[14]Nold J,Strecker M,Liem A,Eberhardt R,Schreiber T,Tünnermann A 2015European Conference on Lasers and Electro-OpticsMunich,Germany,June 21–25,2015 pCJ_11_4

[15]Anderson B,Flores A,Holten R,Dajani I 2015Opt.Express23 27046

[16]Sun Y H,Feng Y J,Li T L,Wang Y S,Ma Y,Tang C,Zhang K 2015High Power Laser and Particle Beams27 071013(in Chinese)[孙殷宏,冯昱骏,李腾龙,王岩山,马毅,唐淳,张凯2015强激光与粒子束27 071013]

[17]Naderi N A,Dajani I,Flores A 2016Opt.Lett.41 1018[18]Harish A V,Nilsson J 2015Opt.Express23 6988

[19]Zeringue C,Dajani I,Naderi S,Moore G T,Robin C 2012Opt.Express20 21196

[20]Du W B,Wang X L,Zhu J J,Zhou P,Xu X J,Shu B H 2013High Power Laser and Particle Beams25 598(in Chinese)[杜文博,王小林,朱家健,周朴,许晓军,舒博宏2013强激光与粒子束25 598]

[21]Jenkins R B,Sova R M,Joseph R I 2007J.Lightwave Technol.25 763

[22]Boyd R W,Rzaewski K,Narum P 1990Phys.Rev.A.42 5514

[23]Mungan C E,Rogers S D,Satyan N,White J O 2012IEEE J.Quant.Electron.48 1542

[24]Tang C K,Reed G T 1995Electron.Lett.31 451

[25]Shimotsu S,Oikawa S,Saitou T,Mitsugi N,Kubodera K,Kawanishi T,Izutsu M 2001IEEE Photonics Technol.Lett.13 364

[26]Xie S P,Xu G L 2013Acta Opt.Sin.33 0206003(in Chinese)[谢淑平,许国良 2013光学学报 33 0206003]

[27]Liu Y F 2008Ph.D.Dissertation(Harbin:Harbin Institute of Technology)(in Chinese)[刘英繁 2008博士学位论文(哈尔滨:哈尔滨工业大学)]

[28]Zeringue C,Dajani I,Naderi S,Moore G,Robin C 2012Opt.Express.20 21196

[29]Salhi M,Hideur A,Chartier T,Brunel M,Martel G,Ozkul C,Sanches F 2002Opt.Lett.27 1294

[30]Ran Y 2015M.D.Dissertation(Changsha:National University of Defense Technology)(in Chinese)[冉阳2015硕士学位论文(长沙:国防科学技术大学)]

[31]Hollenbeck D,Cantrell C 2009J.Lightwave Technol.27 2140

[32]Ran Y,Su R T,Ma P F,Wang X L,Zhou P,Si L 2016Appl.Opt.55 3809

Effect of phase modulation on linewidth and stimulated Brillouin scattering threshold of narrow-linewidth fiber amplifiers∗

Liu Ya-Kun1)Wang Xiao-Lin1)2)Su Rong-Tao1)2)†Ma Peng-Fei1)2)Zhang Han-Wei1)2)Zhou Pu1)2)Si Lei1)2)‡

1)(College of Optoelectronic Science and Engineering,National University of Defense Technology,Changsha 410073,China)
2)(Hunan Provincial Collaborative Innovation Center of High Power Fiber Laser,Changsha 410073,China)

22 May 2017;revised manuscript

7 July 2017)

Stimulated Brillouin scattering(SBS)currently limits the power scaling of narrow-linewidth amplifiers.To date,several techniques have been employed to suppress SBS.Within these SBS suppressing techniques,the phase modulation technique is a preferable approach to obtaining kilowatt-level narrow-linewidth laser sources.In this manuscript,we numerically investigate the in fluence of phase modulation signals on linewidth and SBS threshold,and discuss how to choose an appropriate modulation signal for suppressing SBS with less linewidth broadening.Three types of signals are studied,including sinusoidal signal,white noise signal(WNS),and pseudo-random binary sequence signal(PRBS).Signal parameters such as modulation frequency and modulation depth are also optimized.It is found that the linewidth increases linearly with the modulation frequency,and the linewidth is largest for WNS modulation for the same modulation frequency.Specially,the linewidth is approximate to the modulation frequency for PRBS modulation.In the case of sinusoidal modulation,the spectra exhibit a series of discrete sidebands at integer multiples of the modulation frequency while the spectral power density is almost continuous for WNS modulation.In the case of PRBS modulation,the spectra contain periodic features that are distributed as a function of modulation frequency and pattern length.The SBS threshold grows to a maximum at～100 MHz modulation frequency for the case of sinusoidal signal modulation,which can be further increased by increasing the modulation depth.The SBS threshold can be further increased by implementing the cascade sinusoidal signal modulation.When WNS modulation is employed,the SBS threshold increases almost linearly with the modulation frequency and has an S-shaped increase with the modulation depth.For the PRBS modulation,the pattern length has an optimal value for SBS suppressing:the SBS threshold increases almost linearly below a frequency,but keeps stable above that frequency.The PRBSs with longer pattern lengths tend to suppress SBS more effectively in higher modulation frequency regime than those with the shorter ones.In the commonly used 1—2 GHz frequency regimes,the PRBS with a pattern length of 7 provides the best SBS mitigation,and the pattern length should be longer when the frequency is higher than 2 GHz.It should also be noted that the SBS threshold is highest when the modulation depth is close to the half-wave voltage(π).From the aspect of SBS suppression,the PRBS is superior to other two modulation signals,which can achieve higher SBS threshold with less linewidth broadening.The investigation can present a reference for the phase modulation signal designing in the power scaling of the narrow-linewidth fiber amplifiers.

fiber amplifier,stimulated Brillouin scattering,narrow linewidth,phase modulation

PACS:42.55.–f,42.65.Es,42.79.HpDOI:10.7498/aps.66.234203

*Project supported by the National Natural Science Foundation of China(Grant No.61505260)and the National Key Research and Development Program of China(Grant No.2016YFB0402200).

†Corresponding author.E-mail:surongtao@126.com

‡Corresponding author.E-mail:w_zt@163.com

(2017年5月22日收到;2017年7月7日收到修改稿)

高功率窄线宽光纤放大器的输出功率主要受限于受激布里渊散射(SBS)效应,通过相位调制进行线宽展宽可以有效抑制SBS效应.基于窄线宽光纤放大器中的SBS动力学模型,研究了正弦信号、白噪声信号和伪随机编码信号(PRBS)对窄线宽光纤放大器光谱特性与SBS阈值的影响.研究发现,采用不同信号进行相位调制时,调制频率和调制深度等参数对调制后激光光谱的谱线间隔、谱线数目与光谱平整度的影响存在较大差异,进而影响放大器的线宽特性和SBS阈值.通过对比分析,给出了调制信号的类型选择和参数优化原则,能够为窄线宽光纤放大器的相位调制系统设计提供参考.

10.7498/aps.66.234203

∗国家自然科学基金(批准号:61505260)和科技部重点研发计划(批准号:2016YFB0402200)资助的课题.

†通信作者.E-mail:surongtao@126.com

‡通信作者.E-mail:w_zt@163.com