教学过程比教学结果更有价值——以点到直线的距离教学为例

王弟成

(连云港市教育局教研室 222006)

近期我市举行市级优秀课评选，选择的课题是苏教版教材必修2第二章《解析几何初步》中的“2.1.6点到直线的距离”.教材对内容的处理分两部分，一是先研究具体情况，即求点D(2,4)到直线AB:5x+4y-7=0的距离；二是再研究一般情况，即求平面上任一点P(x0,y0)到直线l:Ax+By+C=0(A≠0,B≠0)的距离.对于解决问题的方法也介绍两种方法，一是直接求解，化点到线的距离为点到点的距离，即求点出点P到直线l的垂足距离；二是间接求解，将点到线的距离转化为直角三角形的高，借助三角形面积求解.在介绍直接法求解后，教材指出“这一方法运算量较大，下面我们通过构造三角形，利用面积关系求出点D到直线AB的距离.”接着介绍面积法求解.对于一般情况教材没有采用直接法，而是直接采用面积法求解，其目的主要是简化计算.课堂教学中各位选手，也主要是就两个方面、两种方法进行教学.在具体问题求解中学生采用的方法比较多，如直接求交点方法，面积法，解三角形方法，函数最值法等.但对一般情况只介绍面积法求解.听课中总有一种感觉教师在介绍求解方法时，是为介绍方法而介绍方法，真的是“介绍”，显得较为生硬.今天站在培养学生数学“素养”的角度如何上这节课呢？笔者对此有一点想法，提出来与大家交流.

1 数学教学要教给学生研究问题的一般方法，让学生学会解决问题

对于求点到直线的距离笔者理解，有两种思路，一是由一般到特殊，二是由特殊到一般.对于一般到特殊，可以直接提出几何问题研究中除涉及两点之间的距离，还涉及到点到线的距离、线到线的距离，如求多边形面积等.如何求平面上一点P(x0,y0)到直线l:Ax+By+C=0(A≠0,B≠0)的距离？教师直接将问题抛给学生，让学生思考如何解决？引导学生先从考虑特殊情况研究起，即当直线l平行于坐标轴的两种情况，再研究一般情况，即直线不平行于坐标轴的情况.对于从特殊到一般，与上面正好相反.特殊的线能解决，特殊的点(如原点)也能解决，一般情况如何解决？对于特殊情况点到直线的距离可以化为点到点的距离，先求出l的垂线，再联立方程求垂足，再求两点间的距离，每次都这样操作，“繁”，自然考虑是否有公式？能推导出公式吗？正像配方法可以求解一元二次方程一样，但还要寻求更直接求解公式一样.我想在这节课的教学中理应有这样的设计思考，立足学生数学素养培养，教给学生研究问题的方法，而不仅仅是求得一个公式，应用公式.这样的设计或明或暗都要让学生感受到，不仅是推导公式，而是在研究问题，学会研究问题.

2 解析几何的学习必须提高学生的运算能力，让学生不惧怕运算

大家知道，自新课程改革以来，学生的运算能力直线下降，主要原因是初中学习侧重平面几何，学生推理能力得到提高，而对于代数内容要求相对较低，运算自然跟不上.新的课程标准又将“运算能力”作为学生核心素养提出来.所以在必修2的《解析几何初步》的学习中除学习解析几何思想、方法外，提高学生的运算能力也是要重点培养的.教材在求D(2,4)到直线AB:5x+4y-7=0的距离时，分四步介绍，第一步求斜率；第二步求垂线；第三步求交点；第四步求距离.思路清楚，步骤明确，学生自己也可以解决.但教材提出“这一方法运算量较大”，笔者觉得不太合适，编者可能考虑后面一般情况，这样解决“运算量较大”，但对于具体问题这四步解决“运算量并不大”，相反是学生基本运算，做好这样的运算就是学生的“童子功”，因为这样的运算比起直线与圆位置关系，直线与圆锥曲线位置关系的运算量太“小儿科”了.

直接求解困难在哪儿？我们梳理一下过程：

设点P(x0,y0)，直线l:

Ax+By+C=0(A≠0,B≠0).

①

过点P且与直线l垂直的方程为

即Bx-Ay-Bx0+Ay0=0，

②

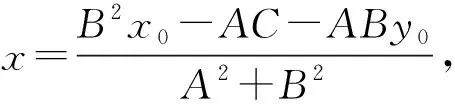
所以

d2=(x-x0)2+(y-y0)2

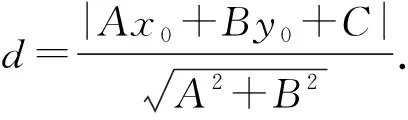
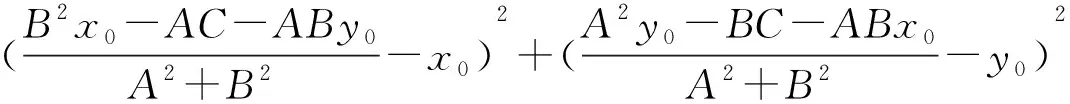
上面直接法的运算思想是每一步都求出来，先求出交点坐标

再将交点坐标代入两点间距离公式

计算.由于繁，自然思考，能不能交换计算顺序，先作差运算？借此机会介绍设而不求思想方法，设而不求方法是解析最重要的方法之一，此处正是渗透设而不求方法的好时机.

设P(x0,y0)，垂足(m,n)在直线l:Ax+By+C=0上，

由Am+Bn+C=0得

A(m-x0)+B(n-y0)=-Ax0-By0-C，

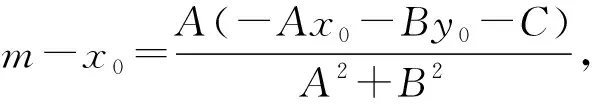
又d2=(m-x0)2+(n-y0)2，

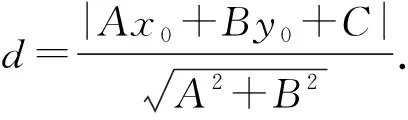
求解后引导学生反思，最终的求解目标是求两点间距离，而不是求交点坐标，即求距离可以求交点的坐标，不求也可以，关键是求m-x0，n-y0，不求x0,y0也能求出(m-x0)2+(n-y0)2的值.后面会遇到此类问题，“过点P(3,0)作直线l，使它被两条相交直线2x-y-2=0和x+y+3=0所截得的线段恰好被P点平分.”可以先设出直线l方程，与两条直线求出交点坐标，再利用中点关系，求出直线l的斜率.也可以先利用中点关系设出点的坐标，再利用点在直线上求出点的坐标，运算量相对较小.

3 求解方法的获得是不同认识的结果，培养学生从不同角度认识问题，培养思维的深刻性

求解点到直线的距离就是求点到垂足的距离，这是直接认识与理解.间接的认识与理解是此距离还有“什么身份”，有什么样的“身份”，就有什么样的认识方法.如果构造三角形，点到直线的距离就是“三角形的高”，因此可以通过面积法求高的值.如果单从直角三角形认识，其是直角三角形的直角边，可以通过解三角形求解.点到直线的距离还是点到直线上任一点距离中的最小值，因此可以通过寻求点与点的最小值求解，即用函数思想求解.不同的认识与理解，会形成不同的求解方法.这就如同找人，不同的身份与关系，会有不同的找法.对于求解解析几何题，这种认识与理解非常重要，很多问题的解决，不是直接求解，而是通过寻找“另一个身份”寻求突破，换一个角度再认识问题.

3.1 运用面积法求解

如图1，一般地，对于直线l:Ax+By+C=0(A≠0,B≠0)外一点P(x0,y0)，

图1

过点P作PQ⊥l，垂足为Q.

过点P分别作x轴、y轴的平行线，

交l于点M(x1,y0)，N(x0,y2).

由Ax1+By0+C=0，Ax0+By2+C=0，

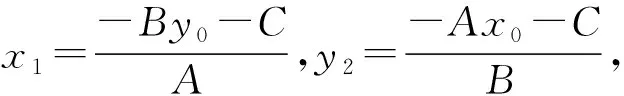
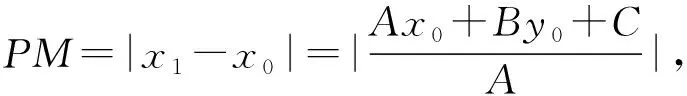
PQ是Rt△PMN斜边上的高，

由三角形面积公式可知

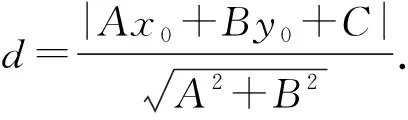
教学中为了让学生自己想到将距离化为三角形的高求解，可以先让学生求原点到直线l的距离，学生最容易想到面积法，再将原点变为一般的点，学生自然想到构造直角三角形用面积法求解.求解后启发学生总结，解决解析几何问题，也要注意平面几何方法的运用，可以简化计算，如直角形三角形中斜边上的中线等于斜边一半，直接应用省去很多计算过程.

3.2 运用函数思想求解.

设P(x0,y0)，点(m,n)是直线l:Ax+By+C=0上任一点，

则Am+Bn+C=0，即Bn=-Am-C.

所以d2=(m-x0)2+(n-y0)2

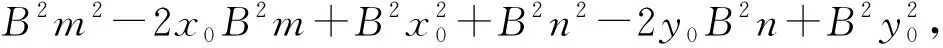
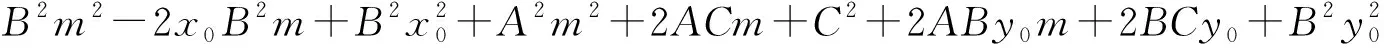
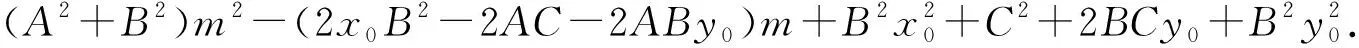
B2d2最小值=

所以

上述的求解过程，对学生来讲有一定的难度，字母多，书写长，运算量大，同时对(a+b+c)2展开式结构要熟悉.但整个求解过程是形式化过程，求B2d2最小值只是为了不出现分式运算，减少书写过程.教学中可以是老师与学生一起运算，让学生看到这样的运算并不可怕，从心理上不惧怕解析几何运算，如果在此回避运算，会让学生形成畏惧心理，不利于后面解析几何的学习.

3.3 解三角形方法求解.

如图2，在△PQM中，PQ是其一条直角边，所以可通过解直角三角形求解.

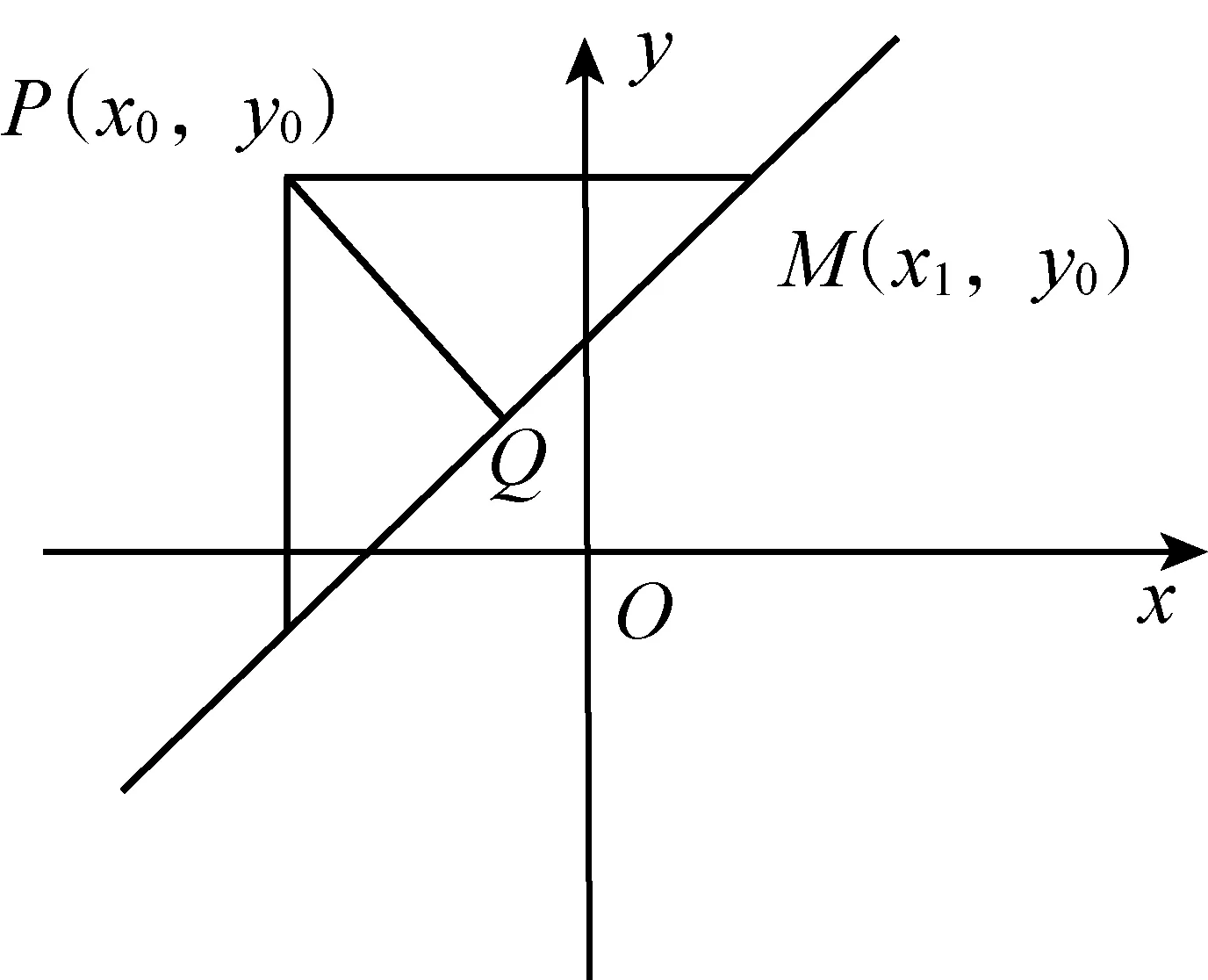
图2

在直角三角形△PQM中得

又PQ=PMsinα

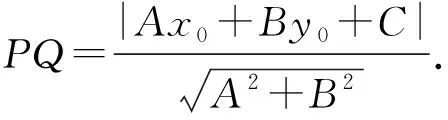
学生虽然没有学习高中的解三角形知识，但初中基础是能理解此种解法的.

就一节课而言，这样的教学可能“偏离”中心，不如教师直接讲解用面积法推导出公式，然后用公式求点到直线的距离，再通过解决其它几何问题培养学生能力来得实用.但若从学生素养培养与学生长远可持续发展角度看，教学倒不如，深入挖掘公式的推导过程价值，落点知识，着眼能力，生长智慧，立足学生数学素养培养，培养学生从不同角度认识与理解问题的深刻性.理解方法的产生源于认识与理解的不同，而不是就方法谈方法、讲方法.这样教学可能一节课完不成，但这样的推导过程比公式结果更有价值，更有利于学生发展，教学的意义正在于此.结果诚可贵，过程价更高.