三角公式的若干几何模型

汪晓勤 邵铭宇

(1.华东师范大学教师教育学院 200062;2.华东师范大学数学系 200241)

在三角学的历史上，许多数学家，如托勒密(C.Ptolemy, 2世纪)、阿布·韦法(Abu Wefa, 940～998)、克拉维斯(C.Clavius, 1538～1612)、韦达(F.Viète, 1540～1603)、克雷斯维尔(D.Cresswell, 1776～1844)等等，都曾利用单位圆来推导三角公式.实际上，打开20世纪中叶以前的任何一部西方三角学著作，我们都能看到，三角公式都是借助某种几何模型、通过线段长度关系、图形面积关系或其他几何命题或公式来推导的[1].考虑到数学教学的原则以及直观想象素养养成的需要，判断一种几何方法是否适合于教学的标准就是它的简洁性与直观性.历史上的许多方法都未能满足这样的标准.

作为对文献[1]所呈现的历史方法的补充，本文在文献[2]以及现代无字证明的基础上，对锐角情形下的和角与差角公式的若干几何模型进行分析，为HPM视角下的三角公式教学设计提供一些思路.

由于和角和差角诸公式中含有sinα，cosα，sinβ和cosβ中两两相乘的项，我们构造两对斜边均为1的直角三角形，其中一对各含锐角为α，另一对各含锐角β，不妨设α≥β.如图1所示.为了获得四个乘积，需要将两对三角形进行组合.

图1 两对斜边为1的直角三角形

1 菱形模型

第一种模型类似于赵爽在其“勾股圆方图注”中所用的弦图，如图2所示，中间补充一个长和宽分别为cosβ-cosα和sinα-sinβ的长方形，得到一个边长为1、一个内角为α+β的菱形，其面积为sin(α+β).将左上直角三角形移至右下，右上直角三角形移至左下，得到一个由三个矩形构成的图形，如图3所示.将该图形分割成左右两个长方形，面积分别为sinαcosβ和cosαsinβ.故得和角正弦公式

sin(α+β)=sinαcosβ+cosαsinβ

(1)

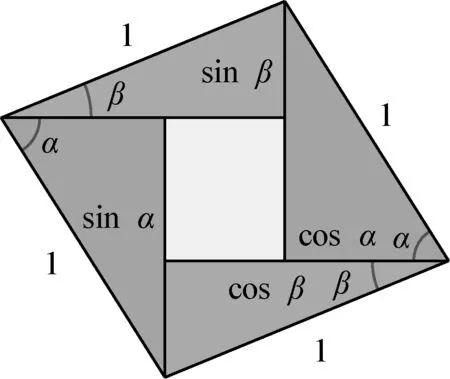
图2 菱形模型

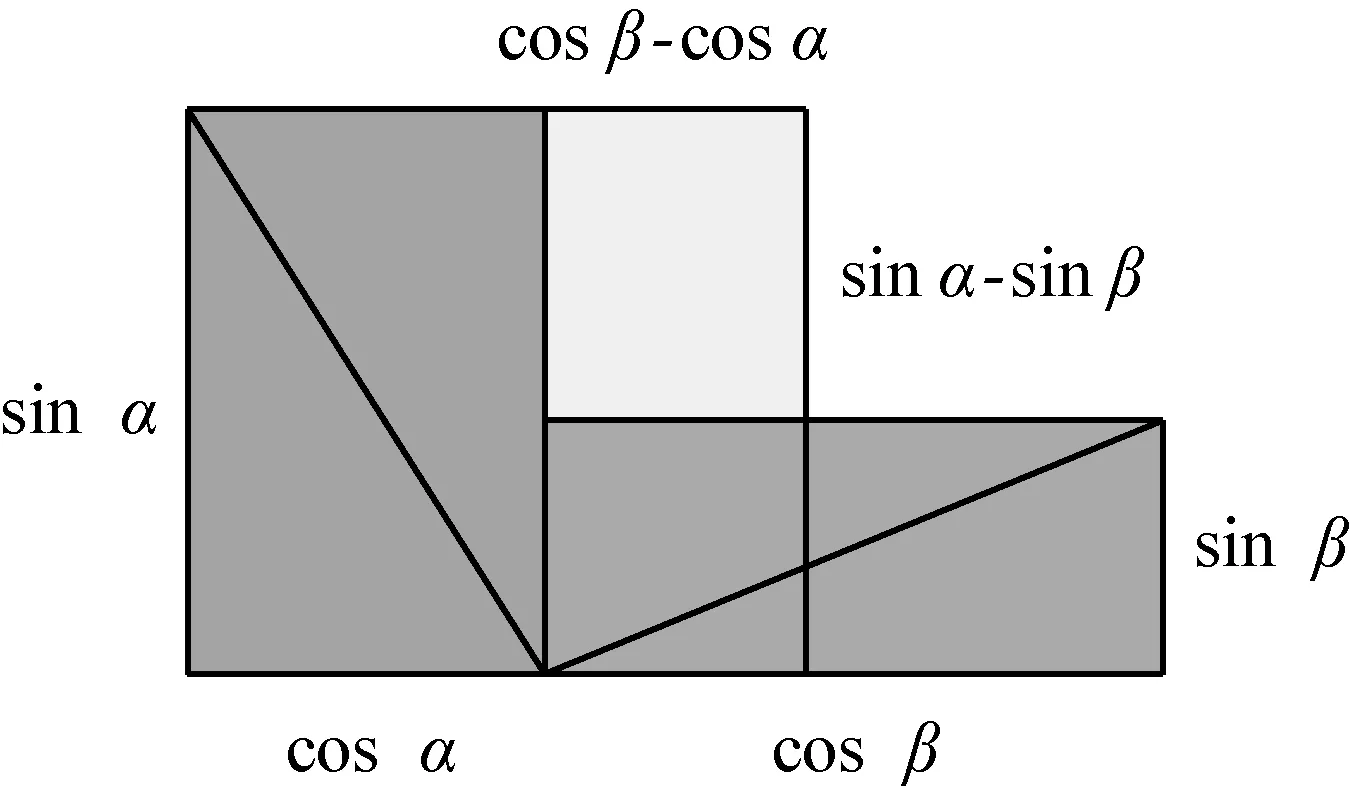
图3 菱形模型的重新组合

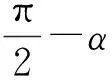
图4 差角余弦的菱形模型及其重组

故得差角余弦公式为

cos(α-β)=cosαcosβ+sinαsinβ

(2)

2 第一类矩形模型

第二种模型类似于赵爽在其“勾股圆方图注”中所用的“大方”图，如图5所示.整个矩形的长为cosα+cosβ，宽为sinα+sinβ；中间是边长为1、一个内角为α+β的菱形，其面积为sin(α+β).在该矩形中，将右上直角三角形移至左下，左上直角三角形移至右下，得到两个深色矩形，余下部分则为两个浅色矩形，其面积分别为sinαcosβ和cosαsinβ，如图6所示.比较图5和图6，易知，图5中的菱形面积等于图6中的两个浅色矩形面积之和，故得公式(1).

图5 第一类矩形模型

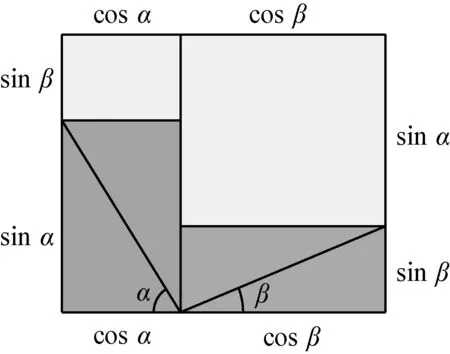
图6 第一类矩形模型之重组

图7呈现了公式(1)的动态形成过程.

图7 和角正弦公式的动态形成过程

我们也可以将上述矩形模型简化为直角梯形模型.如图8所示，将左、右两个深色直角三角形与一个浅色等腰三角形组成一个直角梯形.分别计算各三角形以及整个梯形的面积，得

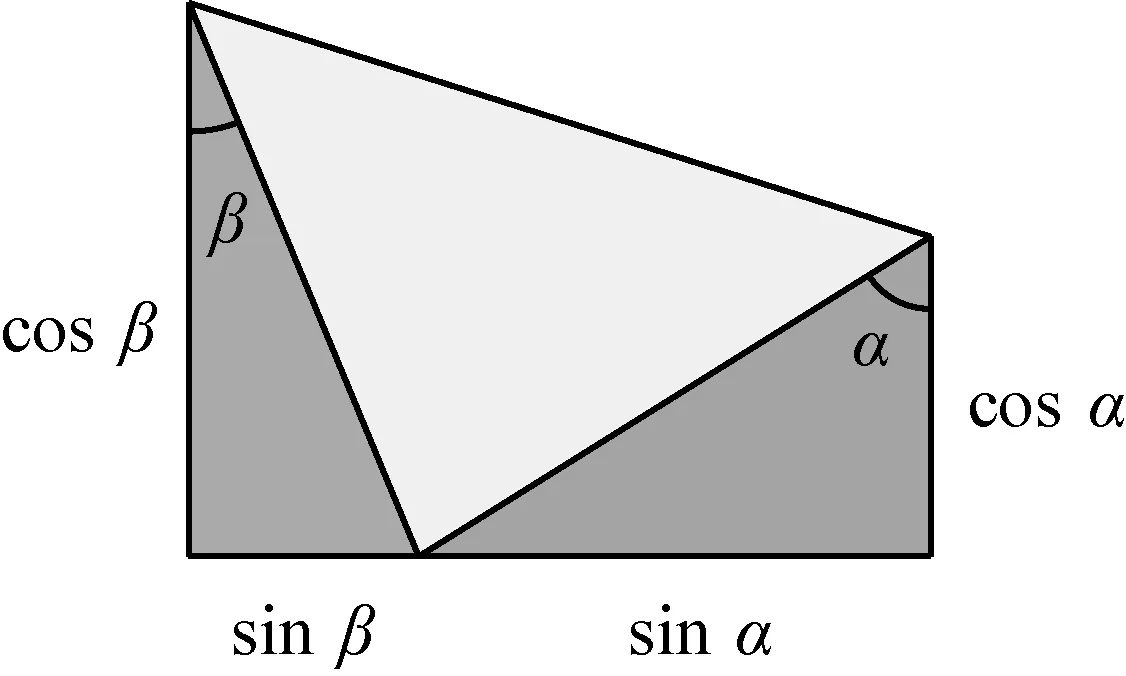
图8 梯形模型

在上述矩形或直角梯形模型中，如果我们不从图形面积关系入手，而是考虑线段之间的关系，也可得相应公式.如图9所示，过顶点A作BD的垂线，垂足为F；过顶点C作AF和DB的垂线，垂足分别为G和H，则由AF=AG+CH即得公式(1)，由BF=CG-BH即得公式

cos(α+β)=cosαcosβ-sinαsinβ

(3)

或者，过顶点D作AB的垂线，垂足为M；过定点E作DM和AB的垂线，垂足分别为N和P，则由DM=EP+DN和BM=EN-BP分别可得公式(1)和(3).

图9 梯形模型中的线段关系

此外，利用余弦定理和勾股定理，可得

AD2=2-2cos(α+β)

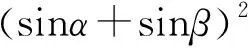
整理后即得公式(3).

3 第二类矩形模型

第三类模型与第二类模型一样，也是一个长为cosα+cosβ、宽为sinα+sinβ的矩形，但两类直角三角形的组合方式不同，如图10所示.其中间是边长为1、一个内角为α-β的白色菱形，面积为sin(α-β)；左上角和右下角均为长和宽分别为cosα和sinβ的浅色小矩形.将同类直角三角形拼成两个深色矩形，如图11所示.易知图10中的白色菱形与图11中的白色矩尺形面积相等，故得公式

sin(α-β)=sinαcosβ-cosαsinβ

(4)

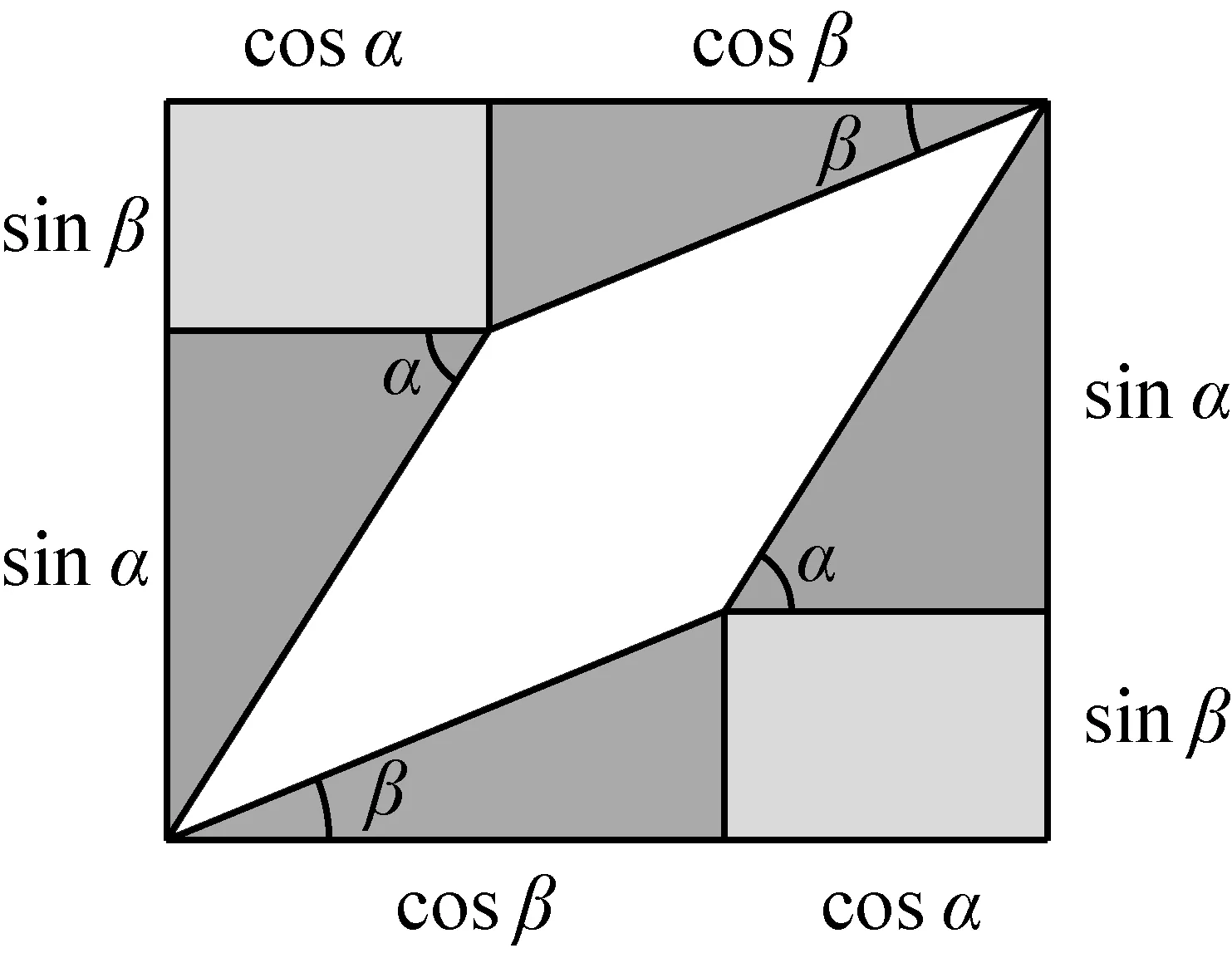
图10 第二类矩形模型

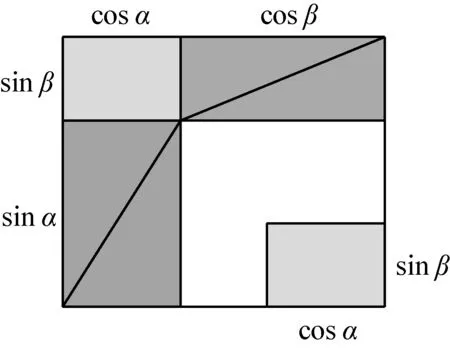
图11 第二类矩形模型之重组

图12呈现了公式(4)的动态形成过程.

图12 差角正弦公式的动态形成过程

若考虑线段之间的关系，则也可得相应公式.如图13所示，过顶点E和G作DF的垂线，垂足分别为R和P；延长BE，交GP于Q，则由RE=PQ=GP-GQ和RD=EQ+PD分别可得公式(4)和(2).

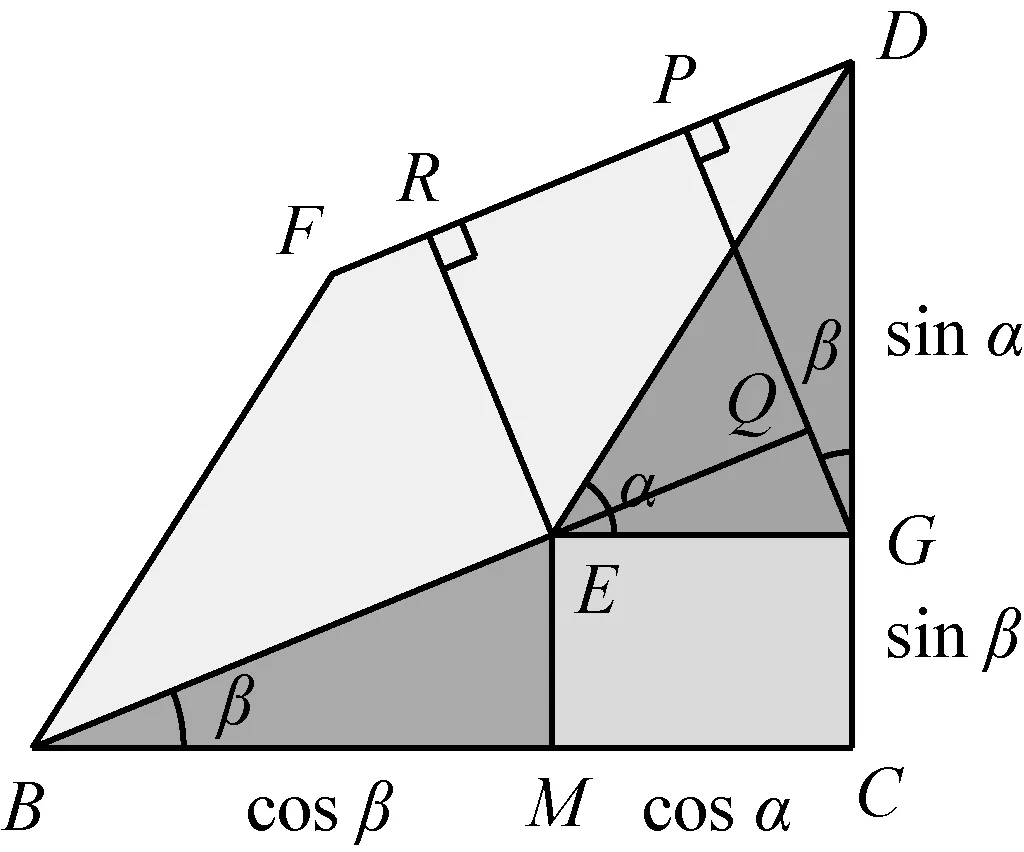
图13 第二类矩形模型中的线段关系

此外，利用余弦定理和勾股定理可得

EF2=2-2cos(α-β)

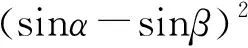
BD2=2+2cos(α-β)

整理后得公式(2).

4 筝形模型

第四类模型如图14所示，两对直角三角形外加一对浅色梯形，构成一个筝形，其面积为

=cosβsecαsin(α+β)，

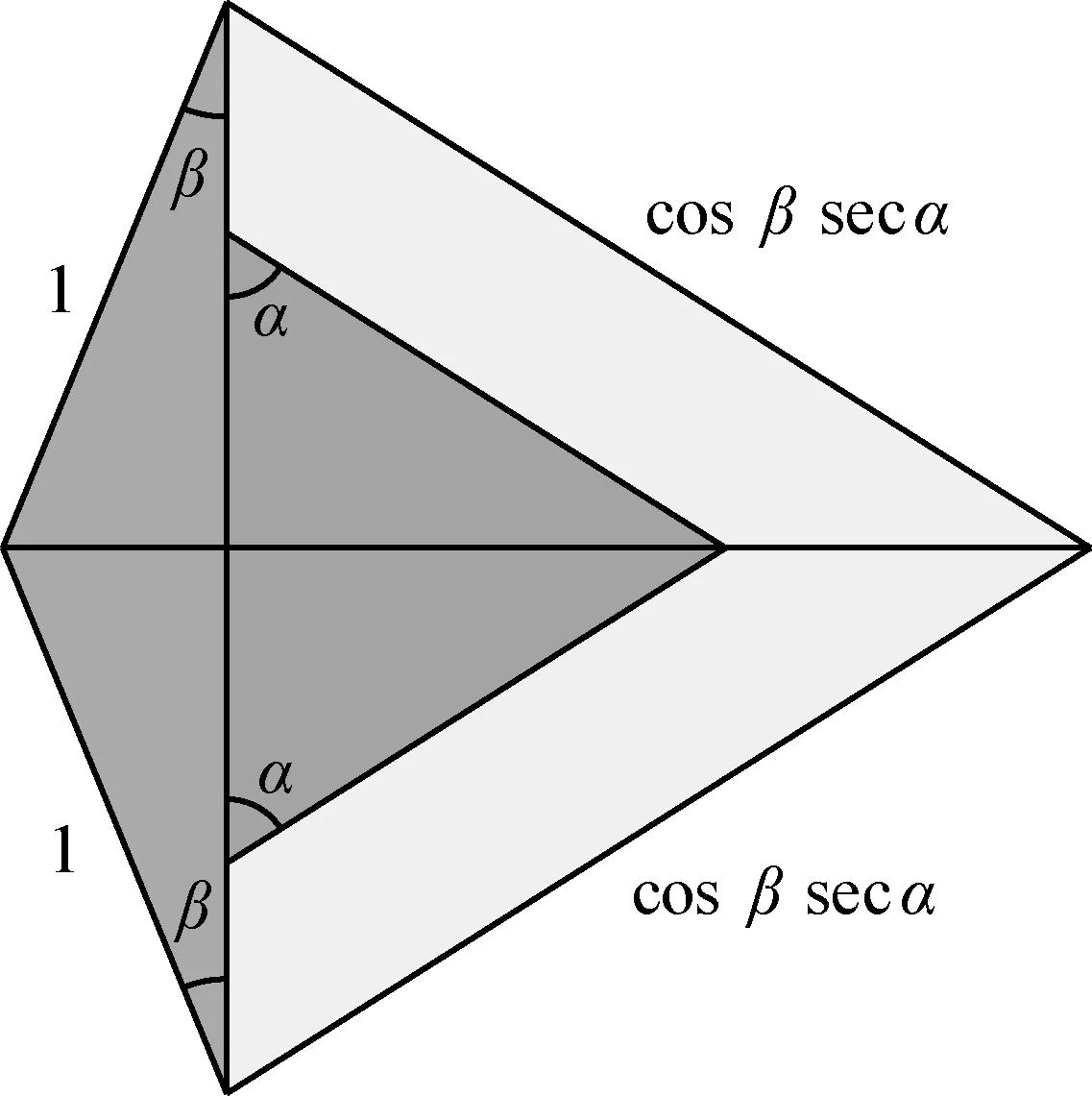
图14 筝形模型

另一方面，筝形面积又等于其对角线乘积之半cosβ(sinβ+cosβtanα)，故有

cosβsecαsin(α+β)=cosβ(sinβ+cosβtanα)，

整理后即得公式(1).

在筝形模型中，若考虑线段之间的关系，则也可得相应公式.如图15所示，过顶点B和C作AF的垂线，垂足分别为G和H；过B作CH的垂线，垂足为K，则由BG=HC+CK和AG=AH-BK分别得(1)和(3).

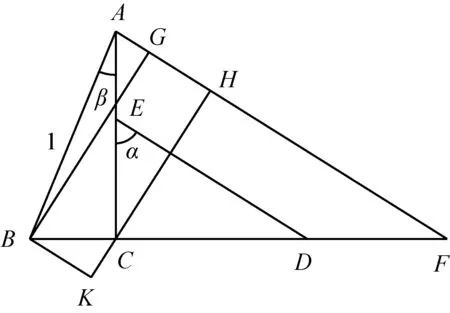
图15 筝形模型中的线段关系

5 平行四边形模型

现在，我们将一个锐角分别为α和β、斜边均为1的两个直角三角形的直角叠合在一起，如图16所示.过第一个直角三角形的非直角顶点，作另一个直角三角形的斜边的平行线，得到第五类模型——平行四边形模型，它是由两个顶角为α-β、腰为1的等腰三角形构成的，面积为sin(α-β)，如图17所示.从平行四边形中割去一个直角边分别为sinα-sinβ、cosβ-cosα的直角三角形，并将其移至右下角，得到一个箭头形的六边形.该六边形由两个小平行四边形组成.分别将这两个小平行四边形进行等积变换，得到一个矩尺形，其面积为sinαcosβ-cosαsinβ，如图18所示.故得公式(3).

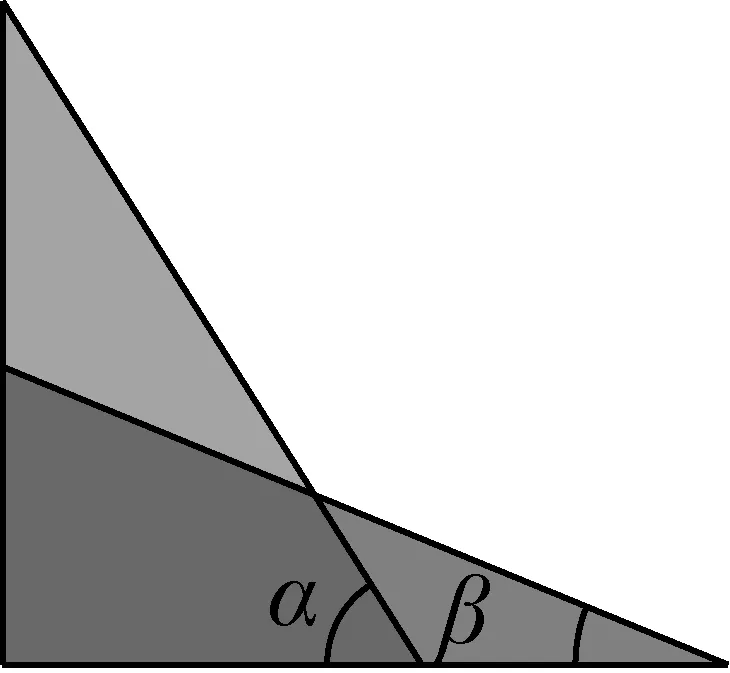
图16 部分重叠的两个直角三角形

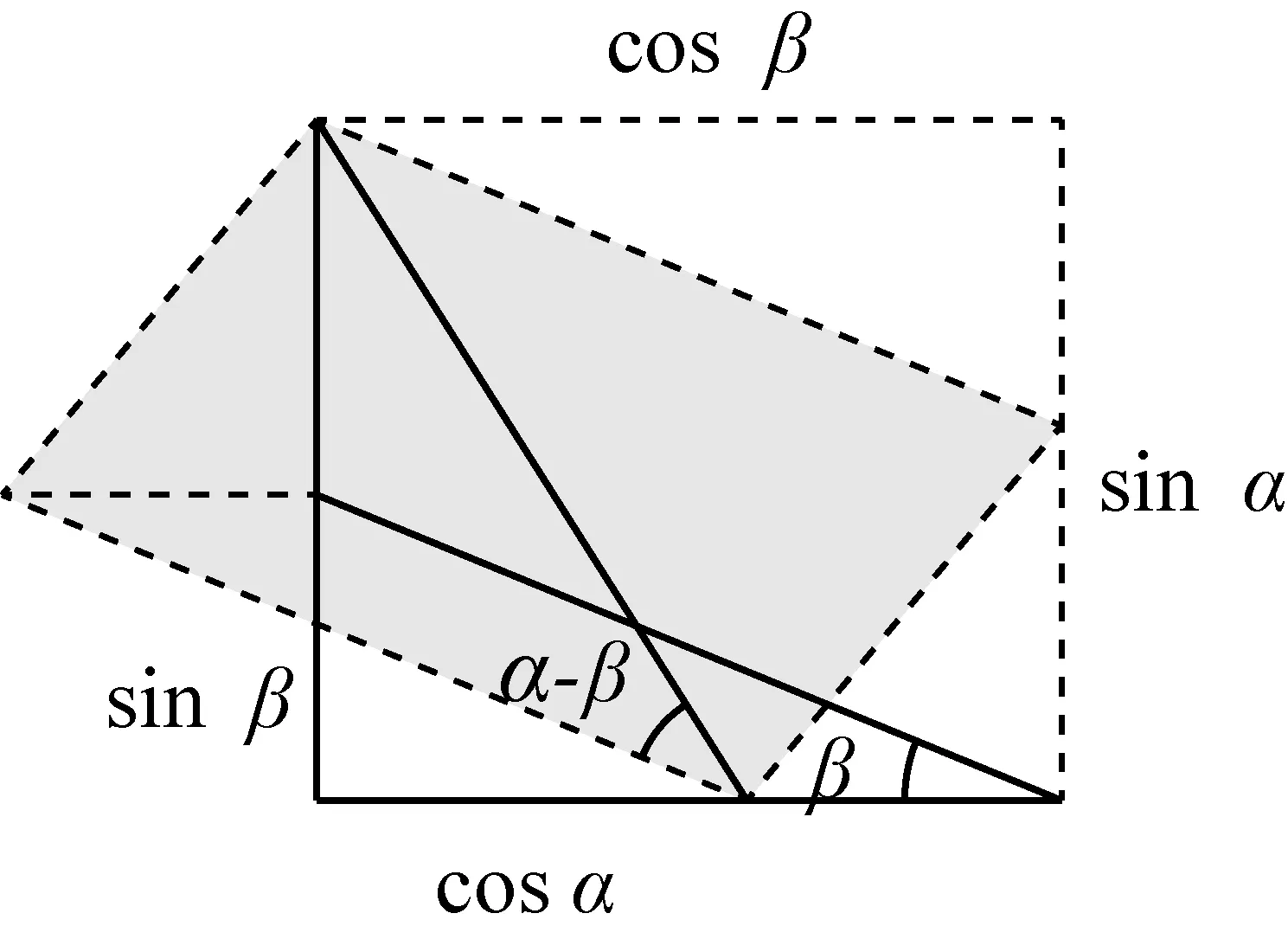
图17 平行四边形模型

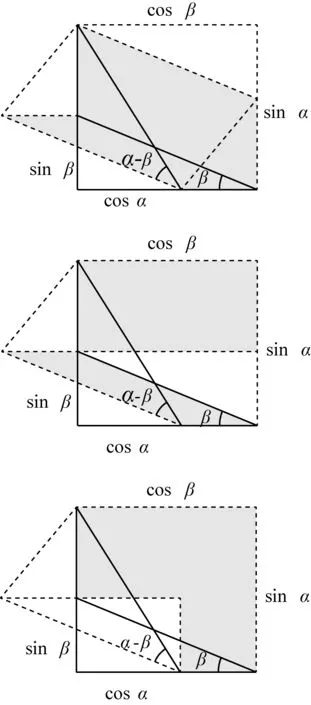
图18 平行四边形的等积变换

在平行四边形模型中，如果我们不从图形面积关系入手，而是考虑线段之间的关系，也可以得到公式(2)和(3).如图19所示，过顶点A作BM的垂线，垂足为F；过顶点C作BM和AF的垂线，垂足分别为H和G，则

cos(α-β)=BF=BH+CG

=cosαcosβ+sinαsinβ，

sin(α-β)=AF=AG-CH

=sinαcosβ-cosαsinβ.

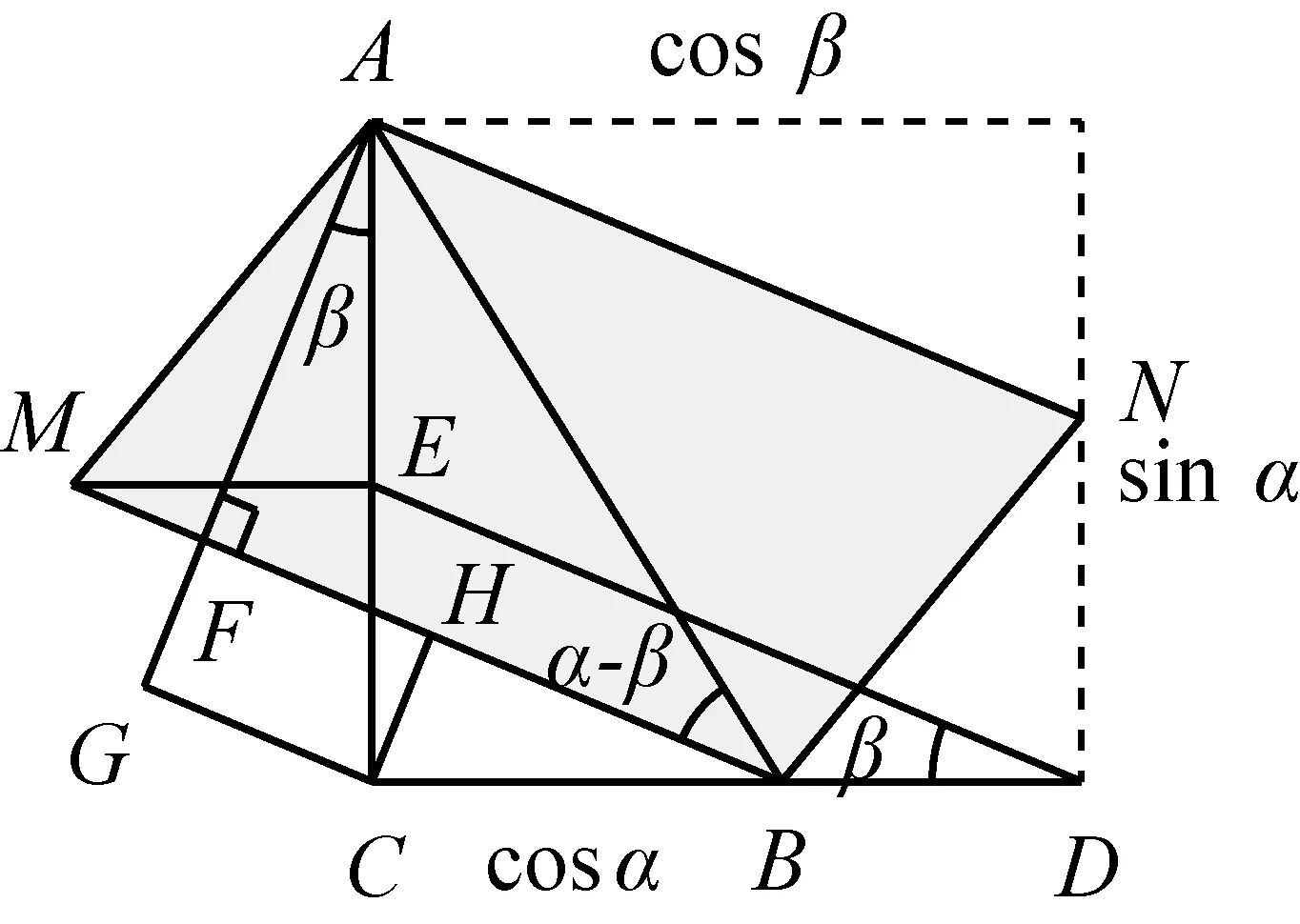
图19 平行四边形模型中的线段关系

6 矩形模型的其他应用

用第二类矩形模型，还可以得到一组和差化积公式.如图20，

图20 用第二类矩形模型推导和差化积公式

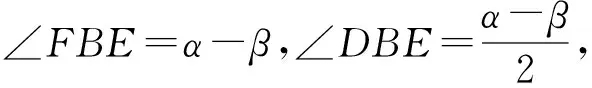
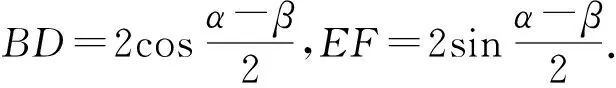
在Rt△DBC和Rt△EFI中分别有

故得公式

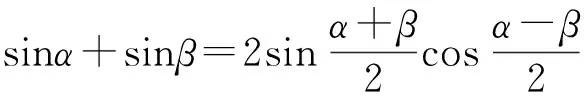
(5)

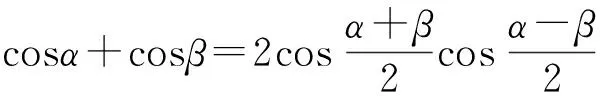
(6)

(7)

(8)

此外，综合运用两类矩形模型，我们可以呈现积化和差公式的形成过程.例如，图21所呈现的是公式

(9)

7 结语

通过两对或两个直角三角形的不同组合，并补充相关图形，我们得到了三角公式的菱形、矩形、平行四边形、筝形、直角梯形模型.基于这些模型，利用面积或线段大小关 系，可以得到和角、差角的正余弦公式甚至和差化积、积化和差公式.就面积关系而言，两类矩形模型最为直观.

在教学中，我们首先需要推导三角形式的三角形面积公式；在此基础上，再导出平行四边形面积公式.然后，引导学生通过拼图，建立矩形模型或其他模型，借助出入相补原理，对图形进行等积变换，将菱形转化为两个矩形之和或差，从而导出锐角情形下的和角与差角公式.这一教学思路，不仅让学生看到三角公式的几何表征，而且还让他们看到公式的形成过程；不仅体现逻辑推理素养，而且还落实直观想象素养；不仅加深学生对三角公式的理解，而且还能让他们树立一种信念——每一个三角公式的背后，一定存在多种几何模型.

图21 积化和差公式的动态形成过程