激光冷却OH分子的理论研究∗
张云光 张华 窦戈 徐建刚
(西安邮电大学理学院,西安 710121)
激光冷却OH分子的理论研究∗
张云光†张华 窦戈 徐建刚
(西安邮电大学理学院,西安 710121)
光谱参数,Franck-Condon因子,辐射寿命,激光冷却
1 引 言
超冷分子的实验制备和理论研究是近年来分子和光物理研究领域中的前沿方向之一.因为分子的内部自由度比原子更多,能级结构更加丰富,可以用来精确测量基本物理常数[1,2],研究偶极-偶极相互作用[3,4],进行量子计算[5]、量子模拟[6],研究冷碰撞[7,8]及冷化学等[9,10],因而对分子的冷却研究吸引了科研人员越来越多的关注.但是相较于原子而言,分子的能级结构非常复杂,很难找到一个闭合的循环跃迁的能级结构,因此分子的激光冷却比原子更难实现.尽管如此,已经证实分子的激光冷却是可行的.2010年,耶鲁大学Shuman等[11,12]首次在实验中用特定波长的激光对SrF分子实现横向冷却,成功打破了激光不可能冷却分子的偏见.2013年,Hummon等[13]进行了YO分子束的一维和二维横向激光冷却和磁光囚禁实验.最近,英国帝国理工学院冷物质中心通过实验验证了脉冲超声CaF分子的纵向减速和冷却[14].随后BH[15]和BaH[16]分子也在实验中实现了激光冷却.除此之外,多种分子的激光冷却得到了理论证明,如MgCl[17],MgBr[17],BeI[18],MgI[18],BeCl[19],BeBr[19],BeF[20],MgF[21]和LiBe[22].然而,不是每一种分子都适合激光冷却.对适合激光冷却的候选分子有严格的要求:首先,分子具有高度对角化的Franck-Condon因子(FCF);其次,分子参与激光冷却的能级带有很高的单光子散射率,即短的辐射寿命.
OH分子氧化能力强,反应速度快,容易氧化各种有机物和无机物,同时在燃烧、有机合成等许多化学反应过程中发挥了非常重要的作用.因此,对OH分子进行高精度光谱测量和高精度电子结构从头计算研究,已成为光谱学和分子物理领域中的一个研究热点.在实验和理论方面对OH分子基态和低激发态的研究已经非常广泛[23−28].早在1979年,已实验测得了OH分子的平衡核间距、振动频率、离解能及电子态的振动和转动光谱常数[23].2003年,其木苏荣等[24]利用从头计算法研究了自由基OH的X2Π和A2Σ+的平衡核间距和跃迁能量.2005年,樊晓伟等[25]采用密度泛函理论的B3LYP方法和二次组态相互作用方法优化计算了OH分子基态(X2Π)的光谱数据.2006年,李权和朱正和[26]用电子相关耦合簇方法CCSD(T)和aug-cc-pVTZ基函数研究了OH自由基分子基态(X2Π)与低激发态(a4Σ−,6Σ−)的结构与势能函数,导出了分子的光谱数据.黄多辉等[27]于2010年利用多参考组态相互作用(MRCI)方法在augcc-pVTZ,aug-cc-pVQZ,cc-pV5Z,6-311++g(d,p)以及6-311++g(3df,3pd)等不同基组水平下,计算OH 分子基态(X2Π)和第一激发态(A2Σ+)的力常数和光谱数据.2011年,Li等[28]用MRCI方法并结合aug-cc-pVQZ基组计算了OH分子X2Π,A2Σ+,14Σ−,12Σ−及14Π这5个电子态的势能曲线.通过以上分析,可以发现对OH分子的基态和第一激发态的研究比较广泛,但缺乏对OH分子激光冷却的研究.因此,本文详细分析OH分子的光谱数据和跃迁性质,制定激光冷却OH的具体方案,为今后激光冷却OH分子的实验研究提供理论依据.
2 计算方法
利用MOLPRO[29]程序包中的高精度MRCI计算方法结合aug-cc-pV5Z基组,计算了OH分子基态和低激发态的势能曲线.为了提高计算精度,在计算过程中首先采用Hartree-Fock方法计算OH分子的基态波函数,然后以此波函数为基础,选用完全活性空间自洽场(CASSCF)[30,31]方法对轨道进行优化,最后以优化的波函数作为参考,对分子进行包含Davidson修正的多参考组态相互作用(MRCI+Q)方法计算[32,33].同时也考虑到核价相关修正、标量相对论效应、三阶 Douglas-Kroll-Hess哈密顿量近似的标量相对论修正.由于程序自身的限制,OH分子的C∞ν群的对称性在实际计算过程中用C2ν群代替,C2ν群的4个不可约表示(A1,B1,B2,A2)和C∞ν点群的不可约表示有如下对应关系:Σ+=A1,Π=B1+B2,Δ=A1+A2,Σ−=A2.在CASSCF和MRCI+Q计算时,OH分子的6个轨道被确定为活性空间(4a1,1b1和1b2),它们分别对应O原子的1s2s2p轨道和H原子的1s轨道.
基于获得的势能曲线,通过Level 8.2[34]程序数值求解一维径向薛定谔方程得到OH分子各个电子态的振动能级、转动常数,继而通过数值拟合得到各个电子态的光谱常数.对于获得的势能曲线,采用的核间距范围为0.03—0.8 nm,步长为0.005 nm.但为了充分描述势能曲线的特性,在平衡核间距附近,计算步长取为0.002 nm.此外在计算中也考虑了自旋轨道耦合效应对基态和低激发态的影响.最后根据修正后的势能曲线和跃迁偶极矩,通过Level 8.2程序计算得到了OH分子A2Σ+→X2Π跃迁的FCF、辐射寿命(τ),以及驱动A2Σ+→X2Π能级跃迁所需的激光波长.
3 结果与讨论
3.1 Λ-S和Ω态的势能曲线和光谱数据
利用MRCI+Q方法,计算OH分子最低两个离解极限O(1D)+H(2S)和O(3P)+H(2S)对应的基态(X2Π)和第一激发态(A2Σ+)的势能曲线,如图1所示.通过获得的势能曲线,利用Level 8.2计算不同电子态的光谱数据列入表1.为了方便与本文结果进行比较,实验结果[23]和其他理论计算结果[25−27,35]也列于表1中.
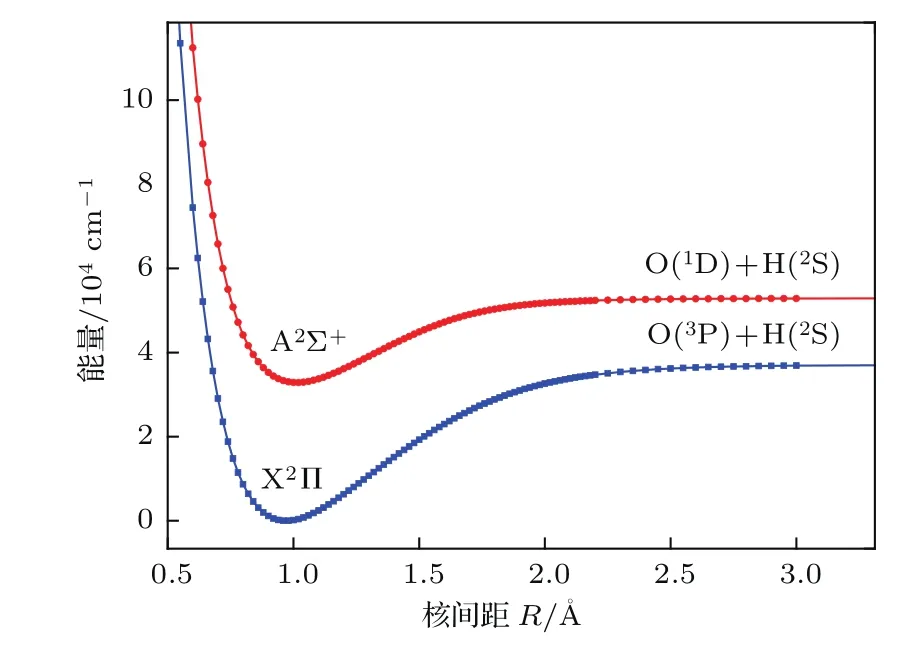
图1 X2Π和A2Σ+电子态的势能曲线(1 Å=0.1 nm)Fig.1.Potential energy curves of the X2Π and A2Σ+states(1 Å=0.1 nm).
在aug-cc-pV5Z,aug-cc-pCV5Z,aug-cc-pVQZ和aug-cc-pCVQZ不同基组水平下,计算得到的光谱数据包括平衡核间距(Re)、谐振频率(ωe)、非谐振常数(ωexe)、转动常数(Be)、离解能(De)和激发能(Te).从表1可以看出,由4种不同的基组计算得到的光谱数据没有明显差别,仔细对比可以发现,借助aug-cc-pV5Z基组得到的ωexe和Be比其他基组的结果更接近实验值.因此,对光谱数据的分析都是基于aug-cc-pV5Z基组的.将计算得到的平衡核间距Re与实验值进行比较,发现基态和激发态的平衡核间距值均稍大于实验值[23],误差仅为0.0722%和0.0790%.对于基态X2Π和激发态A2Π,离解能De为4.5994和2.4486 eV,与理论值4.6503和2.5469 eV[35],4.6568和2.5441 eV[26]很接近.对于基态X2Π,ωexe和Be的值为84.8381和18.8773 cm−1,与实验值84.881和18.910 cm−1基本一致,并且精度高于其他报道的理论值[26,27,35].ωe的值为3753.0041 cm−1,与实验值3737.76 cm−1只相差15.244 cm−1(0.408%).对于激发态A2Σ+,ωe,ωexe和Be与实验值差值为123.521,24.951,0.0291 cm−1.Te的值32860.543 cm−1与实验值32684.1 cm−1符合较好.总体而言,本文计算的光谱数据与实验值符合得相当好.说明采用MRCI+Q/aug-cc-pV5Z方法进行OH分子计算是准确可靠的,可以为后续OH分子的研究提供保证.
考虑自旋轨道耦合后,最低离解极限O(3P)+H(2S)会分裂为两条离解限O(3P2)+H(2S1/2)和O(3P1)+H(2S1/2),且它们的激发能量分别为0和136.9873 cm−1.O(1D)+H(2S)离解极限不发生分裂. 分裂态X2Π1/2,X2Π3/2和的势能曲线绘于图2中. 根据表1,X2Π1/2,X2Π3/2和的平衡核间距Re值与Λ-S态A2Σ+和X2Π的数据完全一致. X2Π1/2和X2Π3/2的De,ωe,ωexe和Be值与X2Π的最小偏差分别为0.0021,0.3814,0.0326,0.0003 cm−1.激发态的ωe和ωexe值分别为3302.3238和117.8658 cm−1,比Λ-S态A2Σ+的值分别高约0.0030和0.0011 cm−1.对于激发态其他的光谱数据,分裂和非分裂态的数据基本上一致.

表1 OH分子Λ-S和Ω态的光谱数据Table 1.Spectroscopic parameters for the Λ-S and Ω states of OH molecule.
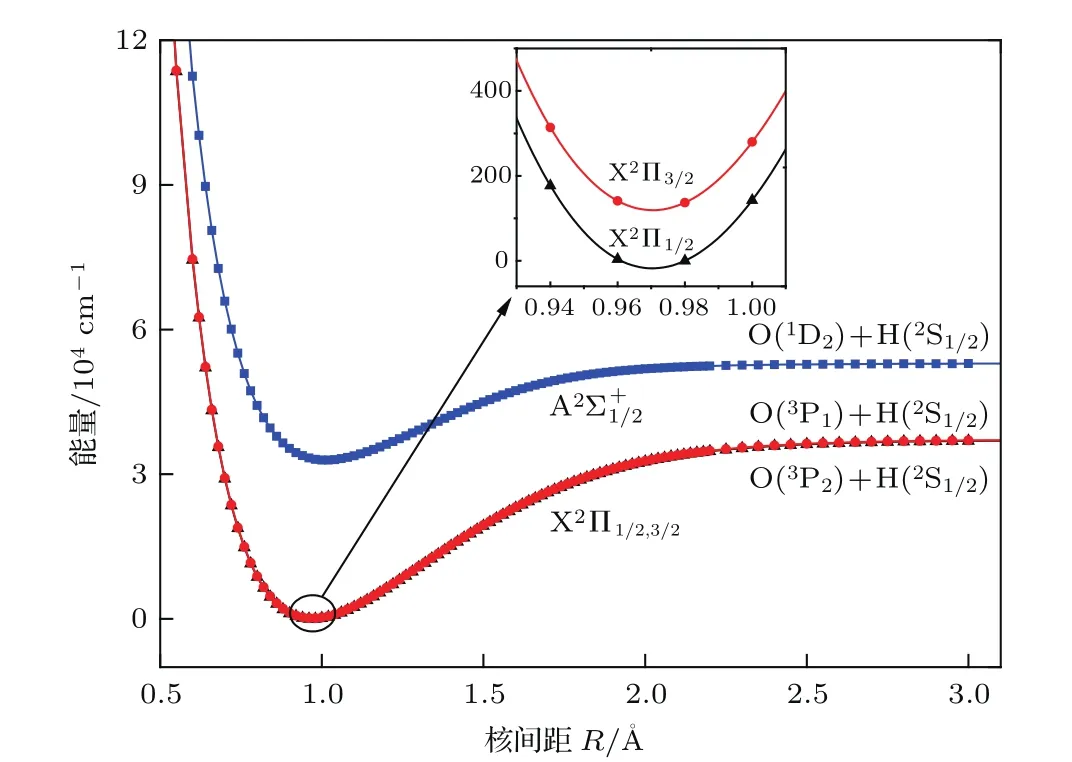
图2 电子态的势能曲线Fig.2.Potential energy curves of the X2Π1/2,X2Π3/2 andstates.
3.2 OH分子振动能级、永久偶极矩和跃迁偶极矩
基于获得的势能曲线,借助Level 8.2程序包,计算了Λ-S和Ω态的所有可能的振动能级,结果都列于表2中. 计算得到X2Π,X2Π1/2和X2Π3/2态的振动能级数为15,A2Σ+和态的振动能级数为8,这是因为激发态的势阱浅于基态的势阱.根据表1和表2,当振动能级数ν=0时,基态振动能级的能量远大于其自旋轨道耦合分裂值(136.9873 cm−1),因此,OH分子基态和激发态之间的跃迁只考虑A2Σ+→X1Π跃迁.
永久偶极矩在激光与分子间的相互作用分析中不可或缺;跃迁偶极矩对于计算爱因斯坦系数也是必不可少的.图3和图4分别为OH分子永久偶极矩和跃迁偶极矩随着核间距的变化.从图3可以看出,基态和激发态的永久偶极矩曲线走势相同,都是先急剧减小到最小值,然后快速增加,在核间距达到3.5 Å (1 Å=0.1 nm)附近,永久偶极矩逐渐趋近于0,这意味着OH分子的解离极限在最远处解离成单独的氧原子和氢原子.从图4可以发现A2Σ→X2Π跃迁的跃迁偶极矩随着核间距的增大而增大,当核间距达到1.84 Å时,跃迁偶极矩达到最大值,将不再增加,而是缓慢减小.最后,当核间距约为4 Å时,跃迁偶极矩趋向于0,这是因为O(3P)到O(1D)自旋禁止跃迁.
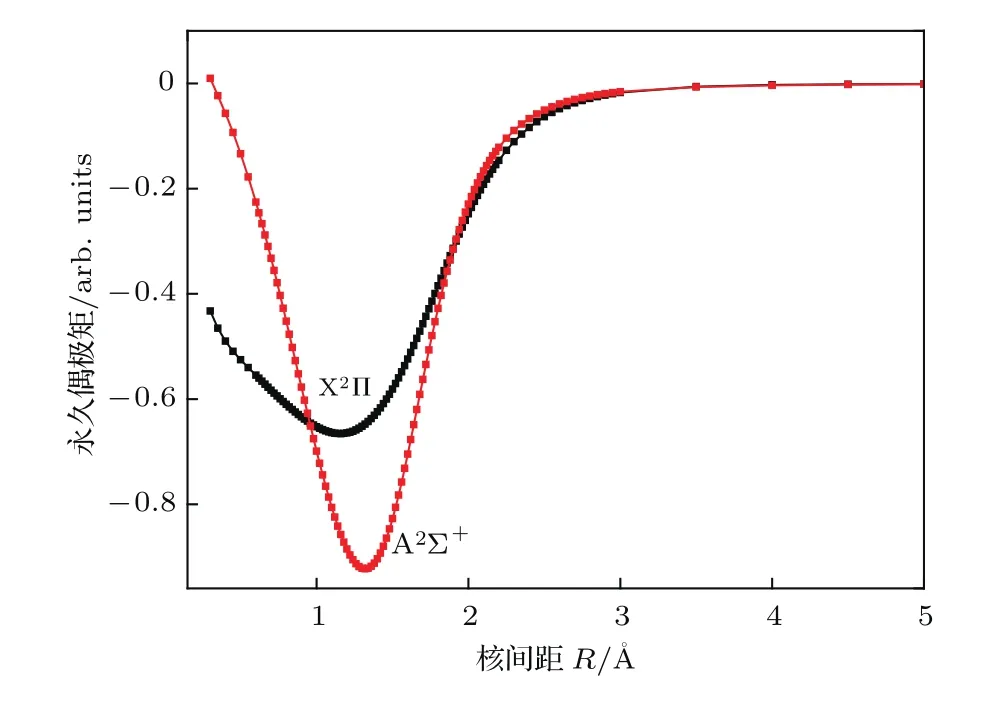
图3 X2Π和A2Σ+电子态的永久偶极矩Fig.3.Permanent dipole moments of the X2Π and A2Σ+states.

图4 A2Σ+→X2Π的跃迁偶极矩Fig.4.Transition dipole moments of the X2Π and A2Σ+states.
3.3 跃迁性质
FCF反映的是两个振动波函数的重叠程度,表示两振动能级之间的跃迁概率.利用基态和激发态修正后的势能曲线以及A2Σ+→X2Π跃迁的跃迁偶极矩,并借助 Level 8.2程序,计算得到A2Σ+→X2Π跃迁在不同振动能级间的FCF.分子能否成为激光冷却的候选分子,主要取决于FCF的对角化程度.为了更直观地看出A2Σ+→X2Π跃迁的FCF分布,将振动量子数在0—9之间所有可能产生的FCF都画在图5中.同时,在计算FCF的过程中也得到了爱因斯坦系数Aν′ν′′,进而求出相应的辐射寿命τ.表3列出了6个最低振动能级间的爱因斯坦系数Aν′ν′′,FCF和辐射寿命τ.
从表3可以看出,本文计算得到的OH分子A2Σ+(ν′=0)→X2Π(ν′′=0)跃迁的FCF为0.9053.对于好的激光冷却候选分子,除了高度对角化的FCF,还应当有显著的激光冷却循环速率(105—108s−1)来产生自发辐射力.因此,短的辐射寿命τ是非常重要的.A2Σ+(ν′=0)→X2Π(ν′′=0)跃迁的爱因斯坦系数Aν′ν′′为1.7134×106s−1,即辐射寿命τ为5.8363×10−7s,这意味着可以产生足够大的辐射力,使分子进行快速的激光冷却.
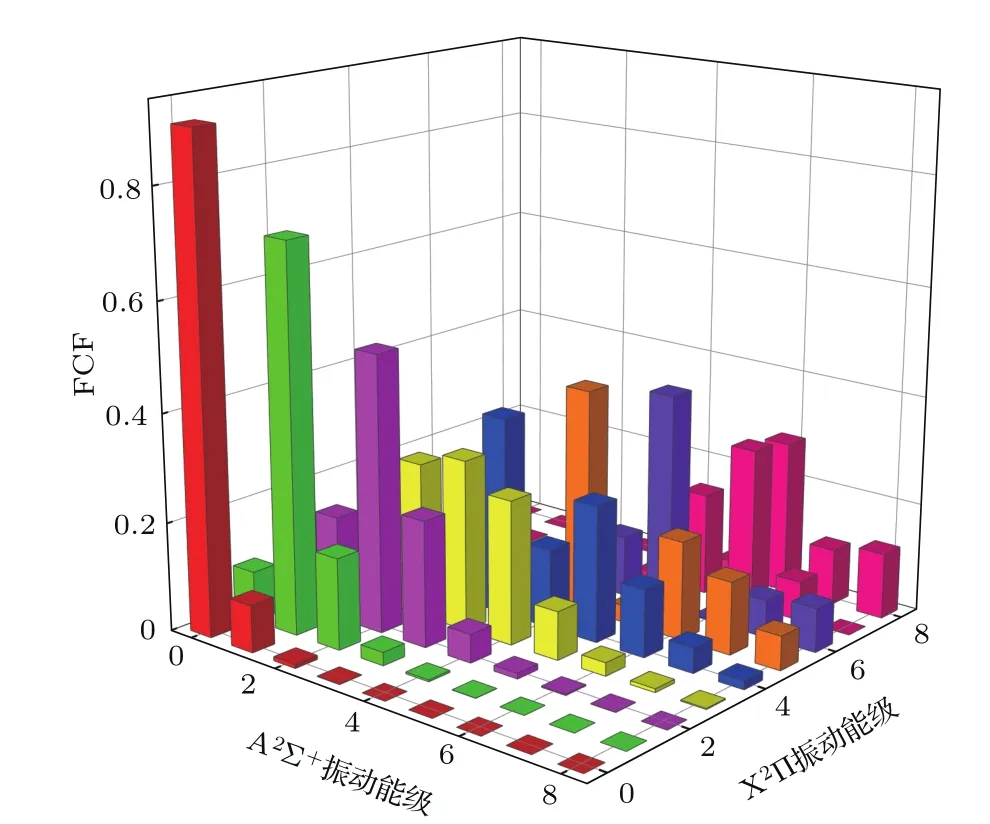
图5 (网刊彩色)OH分子的前8个振动能级下A2Σ+→X2Π跃迁的FCF柱形图Fig.5.(color online)FCFs of OH for the lowest eight vibrational levels of the A2Σ+→ X2Π transition.
3.4 OH分子的激光冷却方案
SrF[11]和YO[13]分子是实验上成功冷却的典型分子,选用了A2Π→X2Σ+准闭合的跃迁能级.而OH分子需要以X2Π和A2Σ+之间的跃迁来建立光学冷却方案.上述计算结果表明,OH分子的A2Σ+→X2Π跃迁具有高度对角化的FCF和短的辐射寿命,满足了激光冷却分子的准则.按照Shuman等[11]的方案,我们为OH分子X2Π态的振动态ν′′=0,1,2,3以及A2Σ+态的振动态ν′=0,1构造了三束激光的冷却循环系统.图6所示为计划方案,其中驱动激光用红色实线表示,自发辐射使用虚线表示.使用波长λ00=307.1532 nm的激光驱动跃迁A2Σ+(ν′=0)→X2Π(ν′′=0). 为了增强冷却效果,又另加了两束重抽运激光,也就是说, 振动态A2Σ+(ν′=0)→X2Π(ν′′=1)使用了波长λ10=344.9163 nm的激光,振动态A2Σ+(ν′=1)→X2Π(ν′′=2)使用的是波长λ21=349.7659 nm的激光.需要注意的是,冷却OH分子使用的激光波长在紫外区域,与冷却SrF和YO分子所使用的红色激光不同,但都容易产生连续波长的激光辐射.此外,如果考虑自旋轨道耦合效应,OH分子基态的能级结构比SrF和YO分子复杂,但OH分子基态的自旋轨道耦合分裂值远小于其振动能级的能量,即可以忽略自旋轨道耦合效应对上述激光冷却方案的影响.冷却OH分子的具体步骤与SrF和YO分子类似,首先在低温腔中用缓冲气体冷却技术得到平动、振动和转动温度较低的分子束源,然后利用光子跃迁准闭合过程产生的自发辐射力使对分子束的运动减速.
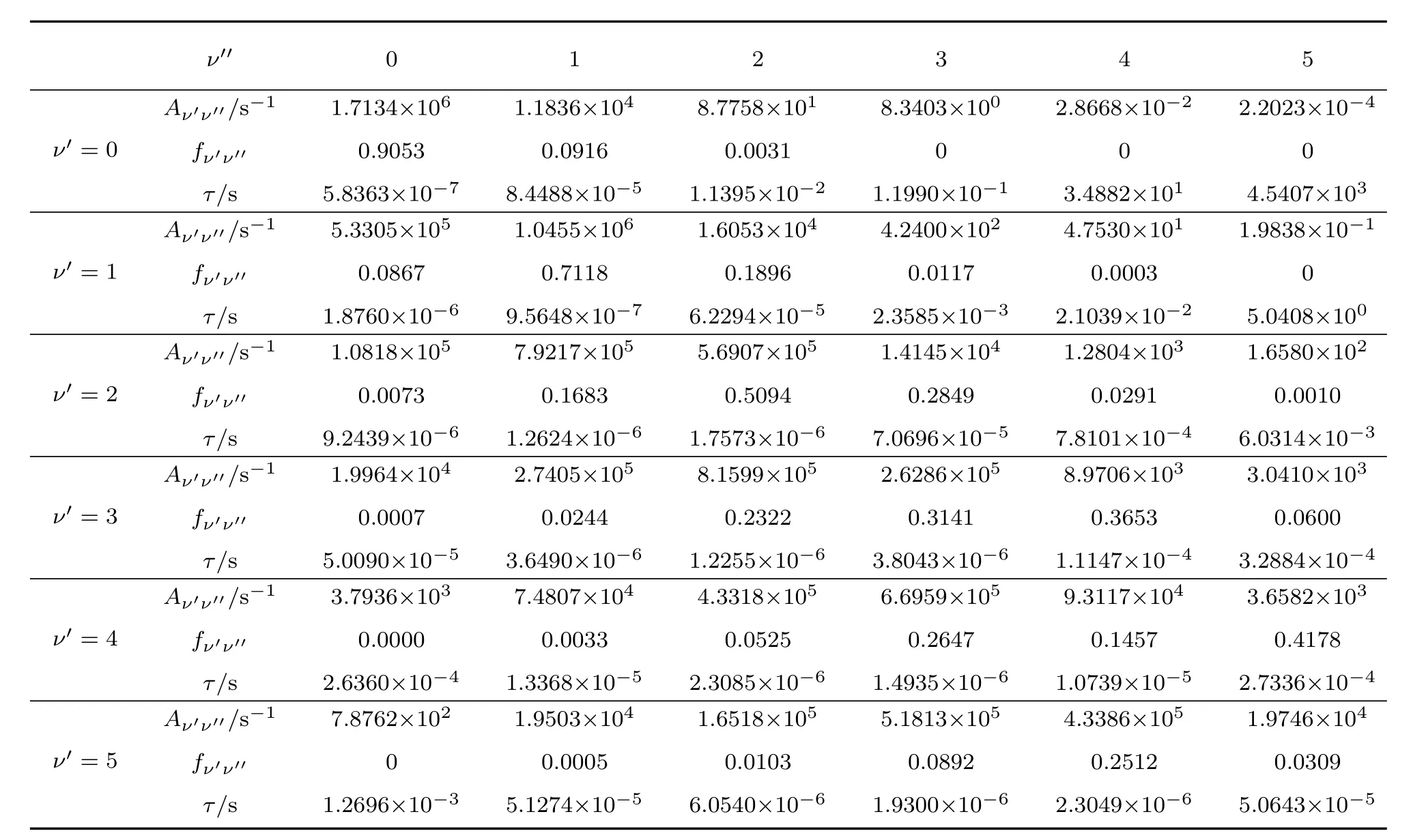
表 3 A2Σ+→ X2Π 跃迁的爱因斯坦系数Aν′ν′′,FCF fν′ν′′和辐射寿命τTable 3.Emission rates Aν′ν′′,FCF fν′ν′′,and radiative lifetime τ of the A2Σ+→ X2Π transition.
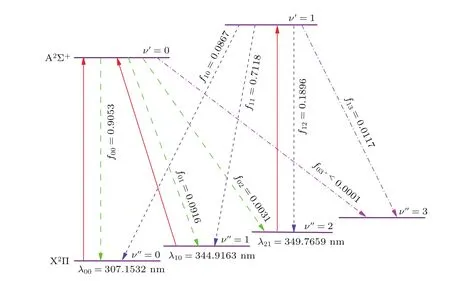
图6 (网刊彩色)激光冷却OH分子过程中驱动A2Σ+→X2Π跃迁需要的激光(红色实线)和自发辐射的FCF(虚线)Fig.6.(color online)Proposed laser cooling scheme using the A2Σ+→ X2Π transition(solid red lines)and spontaneous decay(dotted lines)with calculated fν′ν′′.
4 结 论
采用MOLPRO程序中高精度的MRCI计算方法并结合aug-cc-pV5Z基组,计算了OH分子基态和低激发态的势能曲线.为了得到精确的计算结果,在计算中考虑了Davidson修正,核价相关修正、标量相对论效应和三阶Douglas-Kroll Hamiltonian近似的标量相对论修正.基于MRCI计算的势能曲线,利用Level 8.2程序对一维径向薛定谔方程数值求解,得到OH分子各个电子态的振动能级,拟合得到OH分子的光谱常数,与实验值和其他理论结果比较发现本文结果非常精确.另外,在计算过程中也考虑了自旋轨道耦合效应,发现其对分子结构和光谱常数的影响非常小,同时也分析了OH分子的基态和激发态永久偶极矩和跃迁偶极矩随着核间距的变化规律.
通过已经获得的势能曲线和跃迁偶极矩,基于Level 8.2程序包计算得到A2Σ+→X2Π跃迁的FCF、爱因斯坦系数Aν′ν′′以及辐射寿命τ. 结果表明,OH分子具有高度对角化的FCF(f00=0.9053)和短的辐射寿命τ(τ00=5.8363×10−7s),满足激光冷却分子的准则.最后制定了激光冷却OH分子的具体方案,同时也计算了激光冷却A2Σ+→X2Π能级跃迁所需的激光波长,分别为307.1532,344.9163,349.7659 nm.这些理论数据为OH分子光谱数据的实验测量和超冷OH分子制备奠定了基础.
[1]van Veldhoven J,Küpper J,Bethlem H L,Sartakov B,van Roij A J A,Meijer G 2004Eur.Phys.J.D31 337
[2]Hudson J J,Kara D M,Smallman I J,Sauer B E,Tarbutt M R,Hinds E A 2011Nature473 493
[3]Santos L,Shlyapnikov G V,Zoller P,Lewenstein M 2000Phys.Rev.Lett.28 1791
[4]Baranov M,Dobrek L,Goral K,Goral L,Santos L,Lewenstein M 2002Phys.Scrip.102 74
[5]Micheli A,Brennen G K,Zoller P 2006Nat.Phys.2 341
[6]Baranov M A,Dalmonte M,Pupillo G,Zoller P 2012Chem.Rev.112 5012
[7]Deiglmayr J,Repp M,Wester R,Dulieu O,Weidemuller M 2011Phys.Chem.Chem.Phys.13 19101
[8]Bohn J L 2000Phys.Rev.A63 207
[9]Krems R V 2008Phys.Chem.Chem.Phys.10 4079
[10]Willitsch S,Bell M T,Gingell A D,Procter S R,Softley T P 2008Phys.Rev.Lett.100 043203
[11]Shuman E S,Barry J F,DeMille D 2010Nature467 820
[12]Barry J F,Shuman E S,Norrgard E B,DeMille D 2012Phys.Rev.Lett.108 103002
[13]Hummon M T,Yeo M,Stuhl B K,Collopy A L,Xia Y,Ye J 2013Phys.Rev.Lett.110 143001
[14]Zhelyazkova V,Cournol A,Wall T E,Matsushima A,Hudson J J,Hinds E A,Tarbutt M R,Sauer B E 2013Phys.Rev.A89 12707
[15]Hendricks R J,Holland D A,Truppe S,Sauer B E,Tarbutt M R 2015Frontiers in Physics2 51
[16]Tarallo M G,Iwata G Z,Zelevinsky T 2016Phys.Rev.A 93
[17]Wan M J,Shao J X,Gao Y F,Huang D H,Yang J S,Cao Q L,Jin C G,Wang F H 2015J.Chem.Phys.143 024302
[18]Wan M J,Huang D H,Shao J X,Yu Y,Li S,Li Y Y 2015J.Chem.Phys.143 164312
[19]Wan M J,Shao J X,Huang D H,Jin C G,Yu Y,Wang F H 2015Phys.Chem.Chem.Phys.17 26731
[20]Lane I C 2012Phys.Chem.Chem.Phys.14 15078
[21]Kang S Y,Gao Y F,Kuang F G,Gao T,Du G J,Jiang G 2015Phys.Rev.A91 042511
[22]You Y,Yang C L,Wang M S,Mei S H,Ma X G,Liu W W 2015Phys.Rev.A92 032502
[23]Huber K P,Herzberg G 1979Constants of Diatomic Molecules(Vol.IV)In:Molecular Spectra and Molecular Structure(New York:Van Nostrand Reinhold)
[24]Qimu S R,Zhao Y F,Jing X G,Qin Y L,Li X Y,Su W H 2003J.At.Mol.Phys.20 78(in Chinese)[其木苏荣,赵永芳,井孝功,秦艳利,李新营,苏文辉 2003原子与分子物理学报20 78]
[25]Fan X W,Geng Z D,Zhang Y S 2005Acta.Phys.Sin.54 5614(in Chinese)[樊晓伟,耿振铎,张岩松 2005物理学报54 5614]
[26]Li Q,Zhu Z H 2006Acta.Phys.Sin.55 102(in Chinese)[李权,朱正和 2006物理学报55 102]
[27]Huang D H,Zhang H Y,Wang F H,Zhu Z H 2010Chin.J.Comput.Phys.27 457(in Chinese)[黄多辉,张海英,王藩侯,朱正和2010计算物理27 457]
[28]Li Y J,Zhang P Y 2011J.Theor.Comput.Chem.10 747
[29]Werner H J,Knowles P J,Lindh R,Knizia G,Manby F R,Schütz M 2015MOLPRO,Version2015.1http://www.molpro.net[2017-01-02]
[30]Werner H,Knowles P J J 1985J.Chem.Phys.82 5053
[31]Knowles P J,Werner H J 1985Chem.Phys.Lett.115 259
[32]Knowles P J,Werner H J 1988Chem.Phys.Lett.145 514
[33]Werner H J,Knowles P J 1988J.Chem.Phys.89 5803
[34]Le Roy R J 2015 LEVEL 8.2:A Computer Program for Solving the Radial Schrodinger Equation for Bound and Quasibound LevelsChemical Physics Research Report CP-668,University of Waterloo
[35]Qin X,Zhang S D 2014J.Kor.Phys.Soc.65 2017
Laser cooling of OH molecules in theoretical approach∗
Zhang Yun-Guang†Zhang Hua Dou GeXu Jian-Gang
(School of Science,Xi’an University of Posts and Telecommunications,Xi’an 710121,China)
26 July 2017;revised manuscript
20 August 2017)
Ultracold molecules have wonderfully potential applications in quantum system,precision measurement,and chemical dynamics,and so on.Thus,people have a strong desire for investigating the potential cooling candidates.Feasibility of laser cooled OH molecules is investigated byab initioquantum chemistry.Potential energy curves for the ground state X2Π and low-lying excited state A2Σ+of OH molecules are calculated by multi-reference con figuration interaction method to develop an applicable cooling transition.In order to obtain more accurate results,the calculations involve Davidson corrections,scalar relativistic corrections,core-valence correlation,and spin—orbit coupling effects.Based on the obtained potential energy curves of Λ-S and Ω states,spectroscopic parameters are determined by solving the one-dimensional radial Schrödinger equation,which are in good agreement with available theoretical and experimental values.The permanent dipole moments,transition dipole moments,vibrational levels,Franck-Condon factors and radiative lifetimes of OH molecules are also calculated.The results indicate that the OH molecule has a highly diagonally distributed Franck-Condon factor(f00=0.9053)for the A2Σ+(ν′=0)→X2Π(ν′′=0)transition and short radiative lifetime(τ00=5.8363×10−7s)for the A2Σ+state.It means that the OH molecule meets the criteria as a promising candidate for direct laser cooling,which can ensure rapid and efficient laser cooling.Finally,a speci fic scheme for laser cooling of OH molecules is proposed,and the scheme for the A2Σ+→X2Π transition requires three laser wavelengths,i.e.,main pump laser withλ00=307.1532 nm,two repumping lasers,withλ10=344.9163 nm andλ21=349.7659 nm,respectively.The data imply the probability of laser cooling OH molecules with three electronic levels.In addition,the calculated results also indicate that spin-orbit splitting of X2Π is much less than vibrational level,which leads to the conclusion that spin-orbit coupling has no effect on laser cooling scheme of OH molecules.The results above will provide an important theoretical basis for preparing ultracold OH molecule.
spectroscopic parameters,Franck-Condon factor,radiative lifetime,laser cooling
PACS:31.15.A–,37.10.Mn,87.80.CcDOI:10.7498/aps.66.233101
*Project supported by the National Natural Science Foundation of China(Grant No.11402199)and the Program for New Scientific and Technological Star of Shaanxi Province,China(Grant No.2012KJXX-39).
†Corresponding author.E-mail:zygsr2010@163.com
(2017年7月26日收到;2017年8月20日收到修改稿)
采用高精度的多参考组态相互作用方法计算OH分子基态和第一激发态的势能曲线.为获得更精确的计算结果,在计算过程中考虑Davidson修正、标量相对论效应、核价相关效应和自旋轨道耦合效应.基于计算的Λ-S和Ω态的势能曲线,对一维径向薛定谔方程进行数值求解,得到各个电子态的光谱数据,与已报道的实验值和理论值相符合.获得OH分子的永久偶极矩、跃迁偶极矩、振动能级、Franck-Condon因子及辐射寿命,结果表明,A2Σ+→X2Π跃迁具有高度对角化的Franck-Condon因子(0.9053)和短的辐射寿命(5.8363×10−7s),符合激光冷却分子的条件.制定了激光冷却OH分子的具体方案,计算得到激光冷却跃迁A2Σ+→X2Π所需的三束激光波长,主光束波长为307.1532 nm,两束重抽运激光波长为344.9163和349.7659 nm.计算结果为超冷OH分子的实验制备提供重要的理论依据.
10.7498/aps.66.233101
∗国家自然科学基金(批准号:11402199)和陕西省青年科技新星支持计划(批准号:2012KJXX-39)资助的课题.
†通信作者.E-mail:zygsr2010@163.com
——《势能》

