如何选择和设计有效的数学活动

杨小丽

(北京教育学院数学系 100120)

对于同一个教学内容，现如今有着很多种不同的设计方案，而且每种设计方案看起来似乎都很好，那老师们备课的时候，如何对已有的各种方案进行选择呢？或者如何设计出更适合学生的有效的数学活动呢？下面以“平行四边形的判定”为例，加以阐述.

1 已有的数学活动设计方案

对于“平行四边形的判定”，通过查阅各版本教材和文献、以及笔者的课堂观察，发现有以下几种比较有代表性的数学活动设计方案.

方案一逐个研究三个判定定理

问题1：取四根细木条，其中两根长度相等，另两根长度也相等，能否在平面内将这四根细木条首尾顺次相接搭成一个四边形？说说你的理由，并与同伴交流.

由上述问题得到猜想：两组对边分别相等的四边形是平行四边形，证明后得到判定定理1.

问题2：取两根长度相等的细木条，你能将它们摆放在一张纸上，使得这两根细木条的四个端点恰好是一个平行四边形的四个顶点吗？

由上述问题得到猜想：一组对边平行且相等的四边形是平行四边形，证明后得到判定定理2.

接着应用定理解决有关证明问题.

问题3：如图1，将两根木条AC，BD的中点重叠，并用钉子固定，四边形ABCD看起来是平行四边形.

图1

由上述问题得到猜想：对角线互相平分的四边形是平行四边形.证明后得到判定定理3.

接着应用定理解决有关证明问题.

方案二让学生画平行四边形，叙述画法，思考所画的四边形是否平行四边形

问题1：请同学们画一个平行四边形.

问题2：你是怎么画的？

问题3：怎么判断你画的四边形是平行四边形呢？

通过证明得到平行四边形的判定定理.

方案三从性质定理出发、构造逆命题，证明逆命题是否成立

问题1：通过前面的学习，我们知道，平行四边形的对边相等、对角相等、对角线互相平分，反过来，对边相等，或对角相等，或对角线互相平分的四边形是平行四边形吗？也就是说，平行四边形的性质定理的逆命题成立吗？

经过证明，发现这些逆命题都成立，于是得到平行四边形的3个判定定理：两组对边分别相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形.

问题2：我们知道，两组对边分别平行或相等的四边形是平行四边形，如果只考虑四边形的一组对边，他们满足什么条件时这个四边形能称为平行四边形呢？

由上述问题得到猜想：一组对边平行且相等的四边形是平行四边形，证明后得到判定定理4.

方案四从性质出发、构造命题，证明命题是否成立

问题1：如图2，已知平行四边形ABCD，对角线AC，BD交于点O，试用简洁的符号语言，一一写出该平行四边形的性质.

图2

先由学生回忆、回答，教师追问依据，然后整理写出如下8条结论：(1)AB∥CD；(2)AD∥BC；(3)AB=CD；(4)AD=BC；(5)∠BAD= ∠DCB；(6)∠ABC= ∠ADC；(7)AO=CO；(8)BO=DO.

问题2：问题1告诉我们，如果已知一个四边形是平行四边形，它就具备上述8条性质，那么，反过来思考，在上述8条中，具备几条就可以判断此四边形是平行四边形？试说明你的发现.

学生独立探究后全班交流结果.

2 不同数学活动设计方案的教学效果及思考

《义务教育数学课程标准》(2011版)对平行四边形判定定理的要求是：探索并证明平行四边形的判定定理：一组对边平行且相等的四边形是平行四边形；两组对边分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形1.前述四种数学活动设计方案都能够达成上述目标.那这四种方案不同之处在哪里、教学中的优劣又是什么呢？

方案一对判定定理逐个进行了探究证明，学生能够比较好地掌握单个判定定理的内容和证明.但是这样的活动设计在教学中有以下不足：以问题形式呈现的三个探究活动指向性很强，学生只需要按题目要求操作即可，思维的空间不大，探究的意味不足；此外，三个问题之间缺少关联，学生体会不到它们之间的内在联系.这样的设计不利于学生掌握研究几何图形判定的一般方法，面对一个未知的新图形，如果没有了老师预先设计好的情境，学生将无法展开研究.

方案二建立在学生原有的基础之上，能够充分利用学生的生成资源.但也存在不足：其一，教学效果取决于学生的表现，是否能得到判定定理、得到几个判定定理完全依赖于学生有几种画图方法，如果没有出现教师期望的画法，教师只能“告诉”学生，这就使得探究活动的效果大打折扣；其二，教学效果取决于教师对学生思维的挖掘深度，学生能否获得研究图形判定的方法依赖于教师是否能够将学生模糊、零散的想法追问出来，并归纳形成较为系统的研究方法.如果教师的教学只是停留在单个定理的结论和证明上，则学生获得的也仅仅只是单个定理的结论和证明，这样的教学处理同样不利于学生掌握研究几何图形判定的一般方法，面对一个未知的新图形，学生可能也无法展开研究.

方案三给出了研究平行四边形判定的一种方法：构造学过的平行四边形性质定理的逆命题，然后对这些逆命题进行证明，如若正确，则得到平行四边形的判定定理.这种方法可以迁移到对新图形判定的研究中.但不足之处在于：(1)研究方法是“给出”的；(2)判定定理4：一组对边平行且相等的四边形是平行四边形并不能由上述方法得到.因此，在学习该定理的时候，只能比较突兀地抛出问题：我们知道，两组对边分别平行或相等的四边形是平行四边形，如果只考虑四边形的一组对边，他们满足什么条件时这个四边形能称为平行四边形呢？由该问题得到猜想：一组对边平行且相等的四边形是平行四边形，证明后得到判定定理4.这样的处理方式使得定理4的出现显得非常不自然，似乎凭空而降.

方案四给出了研究平行四边形判定的另一种方法：分别按照边、角、对角线罗列平行四边形的所有性质(一共8条)，然后将这些性质两两进行组合，构造命题(一共28个)，再对命题进行证真或证伪，由此得到平行四边形的判定定理.这种方法可以迁移到对新图形判定的研究中.但该方法工作量比较大，对学生的能力要求比较高，不适合所有的学生.

3 对如何选择和设计恰当的数学活动的建议

3.1 有利于学生积累研究图形判定的活动经验

《义务教育数学课程标准》(2011版)特别强调：数学活动经验的积累是提高学生数学素养的重要标志.帮助学生积累数学活动经验是数学教学的重要目标，是学生不断经历、体验各种数学活动过程的结果[1].李尚志教授也认为：一条重要的核心素养是举一反三的能力，就是能利用旧知识解决新问题的能力，更高一点，利用旧知识生长新知识的能力[2].

因此，在平行四边形判定的教学中，我们有必要将“积累研究图形判定的活动经验”作为教学目标之一，希望学生通过经历有效的数学活动、进一步积累研究图形判定的经验，并能够将这些经验迁移运用到后续的数学学习中去.

我们知道，越基本的方法，适用性就越强，使用范围就越广泛，也就越容易迁移.回顾前述四个方案，只有方案三和方案四的方法最基本，是研究图形判定常用的方法，有利于学生积累研究图形判定的活动经验、并将该方法迁移运用到新图形判定的研究中.

3.2 关注学生已有的认知基础

前面我们提到，方案三、方案四有助于学生掌握研究图形判定的方法、积累研究图形判定的活动经验，但实施起来却都有着各自的不足，那究竟如何选择呢？分析学生已有的数学活动经验是设计有效的数学活动的前提.因此，我们不妨先来看看学生的情况.

学生在学习平行四边形的判定前，学习过等腰三角形、等边三角形等图形的判定，已经具备了一定的研究图形判定的经验.为了进一步了解学生的情况，北师大第四附属实验中学的唐伟老师在上课之前对学生进行了调研.调研问题如下：(1)请你回忆平行四边形的性质有哪些？(2)我们学过用什么方法可以证明一个四边形是平行四边形？(3)请你猜想还有哪些方法可以证明一个四边形是平行四边形，并尝试证明.

调查结果如下：第(1)题正确率100%；第(2)题正确率92.5%；第(3)题结果(班级人数40人)：

猜想内容猜想人数证明人数1两组对边分别相等的四边形是平行四边形31242两组对角分别相等的四边形是平行四边形23103对角线互相平分的四边形是平行四边形21184一组对边平行且相等的四边形是平行四边形975一组对边平行,一组对角相等的四边形是平行四边形756两组对边平行的四边形是平行四边形407一组对边平行,另一组对边相等的四边形是平行四边形208一组对边相等,一组对角相等的四边形是平行四边形20

依据上述调研结果，我们可以发现：(1)学生对判定定理的研究并非零起点；(2)学生得到平行四边形判定定理的途径可能有以下两方面：一是寻找性质定理的逆定理(猜想1，2，3)，二是对平行四边形的单个性质进行组合、构造命题(猜想4，5，7，8).也就是说，学生寻找判定定理的方法与上述方案三和方案四不谋而合.因此，在学生已有的认知基础上进行数学活动的设计，将更有助于活动的实施及学生的学习.

4 设计符合学生实际的有效的数学活动

什么才是“有效的数学活动”？很容易造成的错觉是，“活动”就要动手实践、就要合作、就要小组讨论.其实数学学科的特点决定了数学活动本身有着与其他学科不同的特点.数学活动首先是“数学”的，所从事的活动要有明确的数学目标，到底要不要动手实践、小组合作等都是形式上的保证3.如何通过数学活动深化学生对数学的理解、掌握数学的基本研究方法等才是最重要的.数学建模是很好的数学活动，而一个数学问题的分析和解决过程也是一个“有效的数学活动”.

基于学生已有的认知基础，为了让学生掌握研究图形判定的方法、积累研究图形判定的活动经验，我们可以以问题串的形式设计如下数学活动.

问题1：我们有学过什么方法可以证明一个四边形是平行四边形吗？

【设计意图】

了解学生对定义双重性的认识，并为后续的证明寻找逻辑起点.

问题2：除定义外，还有别的方法可以判定一个四边形是平行四边形吗？你是如何寻找的？

【设计意图】

教育心理学一个最重要的原理是：教师不能只是给学生以知识，而应引导学生用自己的头脑来建构知识4.因此，问题2最核心的目的是：给学生足够的时间调动自己已有的知识经验，对平行四边形的判定方法进行自主研究，然后通过师生交流、更重要的是教师通过对学生解决问题过程的追问和挖掘，逐步将学生模糊的根据性质构造命题的想法清晰化、结构化，从而提炼出平行四边形判定的研究方法.也就是说，研究平行四边形判定的方法是在师生交流的过程中自然“生长”出来的，而不是教师事先给定的.

从学生的回答我们可以发现，学生主要采用以下两种方法寻找平行四边形的判定定理：方法一是构造性质定理的逆定理，方法二是将平行四边形的单个性质进行组合、构造命题.

如若学生采用方法一，教师可以追问：“在学习了平行四边形的性质定理后，构造平行四边形的性质定理的逆命题是一种有效的寻找平行四边形的判定定理的方法.但老师的疑问是：平行四边形的判定定理只有这三个吗？利用这种方法，我们能够找到平行四边形所有的判定定理吗？如果不能，那怎样才能找到平行四边形所有的判定定理呢？”以引导学生思考该研究方法的优点和不足.

如若学生采用方法二，教师可以追问：“你是怎么构造出这个命题的？我们还可以构造出其他的命题吗？如何构造？利用这种方法，我们能够找到平行四边形所有的判定定理吗？”根据学生的回答，逐步将学生模糊的根据性质构造命题的想法清晰化、结构化，从而提炼出平行四边形判定的研究方法，同时体会该方法的优缺点.

在此基础上，还需要让学生进一步思考方法一和方法二之间的关系.方法一和方法二本质上是同一种方法，只不过方法一只能够构造出一部分命题，而方法二能够构造出所有相关命题.

上述无论方法一还是方法二，学生都可以迁移运用到后续图形判定的研究中.

问题3：这些命题都正确吗？如何证明？

【设计意图】

让学生进一步体会证明的必要性，经历证明的完整过程，培养学生的逻辑推理能力.这方面老师们比较重视，处理得也相对较好，此处不再赘述.但要说明的是，在上一个环节，学生构造出了很多命题，但并非所有的命题课上都要加以证明，大多数命题的证明可以留给学有余力的学生课后进行.

问题4：我们是如何研究平行四边形的判定的？

【设计意图】

回顾并提炼平行四边形判定的研究过程，教师可将学生的回答整理如下：

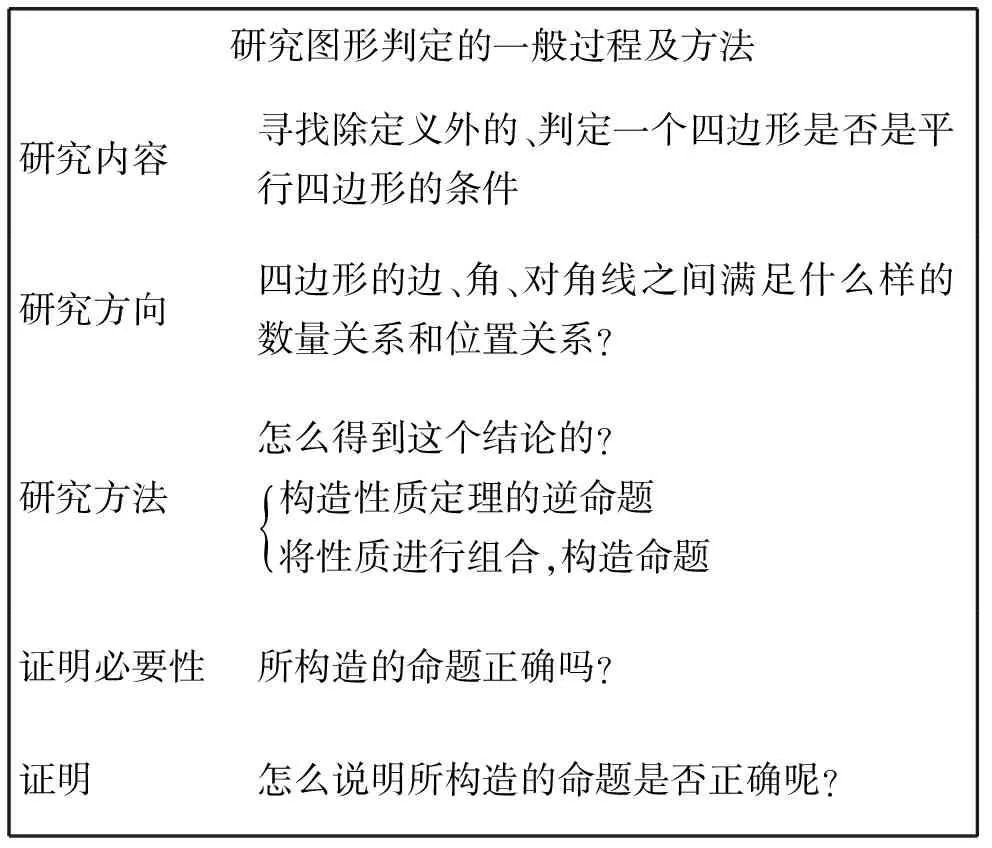
研究图形判定的一般过程及方法研究内容寻找除定义外的、判定一个四边形是否是平行四边形的条件研究方向四边形的边、角、对角线之间满足什么样的数量关系和位置关系?研究方法怎么得到这个结论的?构造性质定理的逆命题将性质进行组合,构造命题{证明必要性所构造的命题正确吗?证明怎么说明所构造的命题是否正确呢?

上述结构化的整理可以帮助学生进一步理清平行四边形判定的研究过程及方法、并将其纳入到已有的认知结构中，为其以后顺向迁移到后续的学习中奠定良好的基础.

在解决上述4个问题的过程中，学生经历了类比、猜测、验证、推理与交流、反思与建构等数学活动，不仅获得了平行四边形判定定理的结论，更重要的是积累了研究图形判定的活动经验.