三角形与其内接相似三角形有关问题的研究
焦青云 郭要红
(安徽师范大学数学计算机科学学院 241000)
设D、E、F分别是△ABC的三边BC、CA、AB边上的点,若△DEF∽△ABC,则称△DEF为△ABC的内接相似三角形.
文[1]给出了任意三角形与其内接三角形相似的一个充要条件,读后颇受启发,由此引发的、需要研究的问题是:三角形的内接相似三角形有多少个?三角形的内接相似三角形的周长与面积有无最大、最小值?本文研究这些问题.
1 任意三角形的内接相似三角形的个数
定理1任意三角形有无数个内接相似三角形.
任意三角形的内接相似三角形的画法,如图1.

图1
在△ABC中,分别过A,B点作BC,AC的平行线交于点M,将△ABM绕B点旋转(旋转后与△ABC不重合)得△A′BM′,旋转角度设为θ.连接M′C交AB于点F′,作F′D′∥BM′交BC于D′,D′E′∥A′B交A′C于E′.连接BE′并延长交AC于E点,作EF∥E′F′交AB于F,FD∥F′D′交BC于D,则△DEF为△ABC的内接相似三角形.
证明显然△BA′M′∽△BAM.
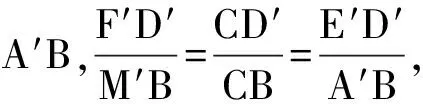
因为EF∥E′F′,FD∥F′D′,
所以∠D′F′E′=∠DFE,

从而∠E′D′F′=∠EDF,△DEF∽△D′E′F′,
于是△DEF∽△ABC.
旋转角θ不断变化,定理1得证.
2 三角形的内接相似三角形的周长、面积的最大、最小值

证明设a,b,c分别为∠A,∠B,∠C对应边的边长,α,β,γ分别为∠A,∠B,∠C的角度,其中β≤α≤γ.P,S为△DEF的周长与面积,P′,S′为△D′E′F′的周长与面积.先讨论θ的取值范围.
显然θ的最小值为0,随着θ不断增大,当E′在AB上时,θ有最大值,此时内接相似三角形与原三角形的一组对应顶点共边.如图2,
θ=∠MBM′=∠MBN-∠M′BN
=∠MBN-∠F′D′B
=∠MBN-(∠E′F′D′-∠ABC)
=γ-(γ-β)=β
所以θ∈[0,β].
如图3建立平面直角坐标系.

图3
因为F′为lAB和lM′C的交点,于是
其中
T=bsin(α+β+θ)-tanβ(bcos(α+β+θ)-a).
并由正弦定理可得
P′ =|D′E′|+|D′F′|+|E′F′|


由yE′=|D′E′|sin(β+θ),
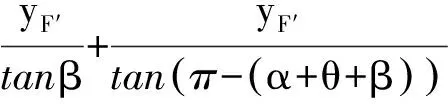
+|D′E′|cos(β+θ),
得
与lAC联立解得
其中H=csinβsin(α+θ)-csinγsinθ+
asinγsin(β+θ).
令H′≤0,解得θ≥0.
于是P与S在θ=0处取得最小值,在θ=β处取得最大值,代入得
定理2得证.

