对平面向量数量积发生发展之思考

张曜光

(金华市教育局教研室 321017)

1 引言

平面向量数量积是向量理论中的一个重要概念，在学习了平面向量的基本概念，平面向量的线性运算，平面向量的基本定理及坐标运算之后，再学习平面向量数量积，向量将完全展现“如果没有运算，向量只是一个‘路标’，因为有了运算，向量的力量无限.[注]刘绍学主编. 普通高中课程标准实验教科书数学4 A版[M].北京：人民教育出版社，2007”

对于平面向量数量积的教学，2003年课标要求：“通过物理中‘功’等实例，理解平面向量数量积的概念及其物理意义.”修改中的新课标增加了“会计算平面向量的数量积”.更早的大纲要求也大致相同.

从我国教材引入向量教学起，教师对引入数量积的必要性、数量积究竟是什么等一直存在疑惑.能否给它一个数学化的表达和完整的数学结构？本文对此进行一些探讨，不当之处敬请批评指正.

2 困惑的成因

2.1 物理背景作用的困扰

向量理论具有深刻的数学内涵、丰富的物理背景.向量既是几何研究对象，也是代数研究对象，是沟通几何与代数的桥梁.

在向量的教学中，在物理背景下学习平面向量的基本概念、平面向量的线性运算是必要的，数学的学科逻辑与学生的认知逻辑可以达到完美的融合.

而到了平面向量数量积的教学，两种逻辑就都显得尴尬了.

从学科逻辑来看：

1)这里需要来个元概念吗？

2)这里还是物理的需要，不是数学的必然吗？

从认知逻辑来看：

1)与前面学习的平面向量的线性运算联系不上了；

2)物理是实证科学，类如“力对物体所做的功”的物理模型应该数学演绎佐证，难道是来一个“物理模型”就给它一个数学定义，成为一个数学的新起点？

物理背景在数学教学中的价值应该是便于在背景中进行“数学抽象”，也就是从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系，从事物的具体背景中抽象出一般规律和结构，用数学语言予以表征.但这次不是抽象而是强加，很不自然.

2.2 数学的思维方式的断裂

数学的思维方式可以概括成：观察客观现象，从中抓住主要特征，抽象出概念或数学模型；然后进行探索，探索时常用的是直觉判断、归纳、类比和联想；探索后可以做出某种猜想, 但是需要证明, 这要进行深入分析、逻辑推理和计算；之后才可以揭示出事物的内在规律. 这就是数学思维方式的全过程[注]丘维声. 代数学的发展与数学的思维方式[J].数学通报，2006，45(12).

沿革至今的平面向量数量积教材和教学，只是做了一次“物理模型”的抽象表达，不是从数学内部需要而产生，没有体现数学知识发生发展的必然性，没有遵循数学的思维方式，不利于学生对平面向量数量积内涵的理解和后续内容的学习.

3 平面向量数量积的数学发生方案

3.1 回归知识序

在进行平面向量数量积教学时，平面向量的教学已经走了：平面向量的基本概念平面向量的线性运算平面向量的基本定理及坐标运算的路径，两个向量的加法运算可以是平面向量数量积教学的出发点.

3.2 两个非零向量关系的探究

图1

3.3 几何问题的提出[注]项武义. 基础几何学[M]. 北京，人民教育出版社，2004

我们知道，在平面几何中，三角形是一个精简的基本图形.用向量来表达三角形，则它的三个有向边就可以分别表达为a,b和a+b.如图2-1，由平面几何中所熟知的SSS，△ABC由其三边|a|,|b|,|a+b|所唯一确定，a与b的夹角θ也随之唯一确定.

由勾股定理，若θ=90°，则有|a+b|2=|a|2+|b|2(如图2-2).

若θ≠90°，则|a+b|2-|a|2-|b|2≠0.例如当a=b时，|a+b|2-|a|2-|b|2=4|a|2-|a|2-|b|2=2|a|2.

3.4 几何模型的提出

图2-1

图2-2

3.5 “投影”的概念

考察以a,b和a+b为有向边的△ABC，表面上看“|a+b|2-|a|2-|b|2”的值，由|a|,|b|,|a+b|所决定，但考虑到a+b由a,b决定，可以猜测“|a+b|2-|a|2-|b|2”的决定要素为：a,b，也就是|a|,|b|和θ.

接下去的工作是设法把f(a,b)用|a|,|b|和θ来表示，这样的工作事实上就是要解△ABC，但目前的工具只有勾股定理，所以面对锐角三角形、钝角三角形的情形，有必要构造出直角三角形的问题来加以处理.为此我们引入“投影”的概念.

就θ为锐角、钝角、直角作图如下：

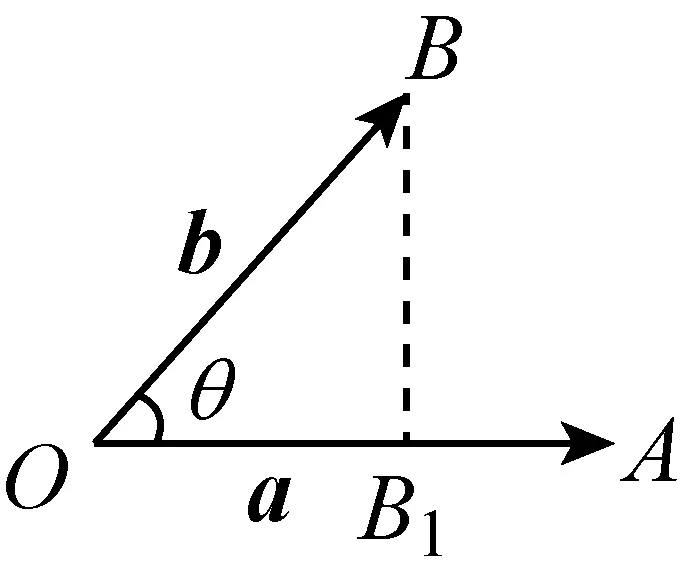
图3-1

图3-2

图3-3

定义1：|b|cosθe叫做向量b在a方向上的投影∗修订中的课标把投影明确为是一个向量，本文把一直沿用的|b|cosθ 另定义为标量投影.，其中e为a方向上的单位向量.

定义2：|b|cosθ叫做向量b在a方向上的标量投影.

投影是一个向量，而标量投影是一个数量，当θ为锐角时标量投影为正值；当θ为钝角时标量投影为负值；当θ为直角时标量投影为0；当θ= 0°时标量投影为|b|；当θ= 180°时标量投影为-|b|.

3.6 几何模型的提炼

接下去的工作是解三角形(不再考虑θ为直角的情形)，考虑到AD边的不同构成方式，分以下图示三种情形：

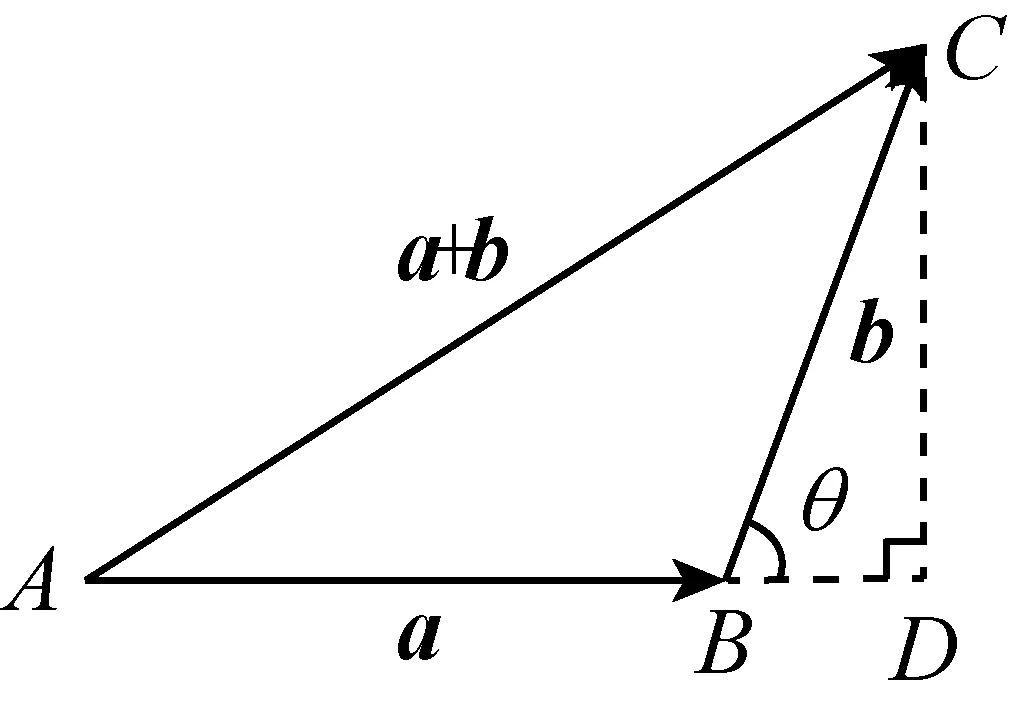
图4-1

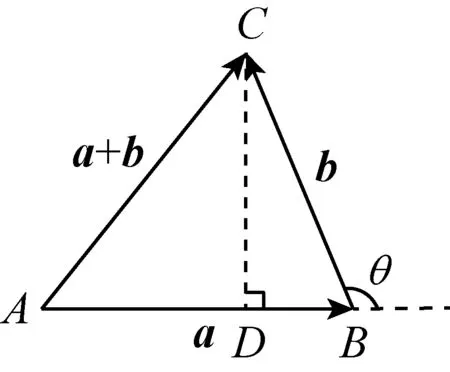
图4-2

图4-3

在三种情形下，都过C作CD⊥AB于D，

在Rt△ADC中，由勾股定理，有|AC|2=|AD|2+|DC|2.

即 |a+b|2=(|a|+|b|cosθ)2+(|b|sinθ)2=|a|2+2|a||b|cosθ+|b|2(cos2θ+sin2θ)=|a|2+2|a||b|cosθ+|b|2

所以 |a+b|2-|a|2-|b|2=2|a||b|cosθ.

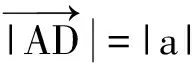
在Rt△ADC中，由勾股定理，有|AC|2=|AD|2+|DC|2.

即 |a+b|2=(|a|+|b|cosθ)2+(|b|sinθ)2=|a|2+2|a||b|cosθ+|b|2(cos2θ+sin2θ)=|a|2+2|a||b|cosθ+|b|2

所以 |a+b|2-|a|2-|b|2=2|a||b|cosθ.

在Rt△ADC中，由勾股定理，有|AC|2=|AD|2+|DC|2.

即 |a+b|2=(-|a|-|b|cosθ)2+(|b|sinθ)2=|a|2+2|a||b|cosθ+|b|2(cos2θ+sin2θ)=|a|2+2|a||b|cosθ+|b|2

所以 |a+b|2-|a|2-|b|2=2|a||b|cosθ.

事实上，以上的解三角形的过程，就是余弦定理的推导过程.f(a,b)与余弦定理有内在联系，这也就提示我们后续用向量的方法推导正、余弦定理必然会是简洁的.

3.7 平面向量数量积(内积)的定义

已知两个非零向量a与b，它们的夹角是θ，则数量|a||b|cosθ叫a与b的数量积，记作a·b，即有a·b= |a||b|cosθ，(0≤θ≤π).并规定0与任何向量的数量积为0.

在这里只不过是把f(a,b)代换一个新符号，平面向量数量积“a·b”就是f(a,b)，如3.5所述，a·b是两个向量a、b上的函数并返回一个标量的二元运算.

3.8 平面向量数量积的几何意义

数量积a·b等于a的长度与b在a方向上标量投影|b|cosθ的乘积.

3.9 平面向量数量积的物理背景

图5

物体在力F的作用下产生位移s,力F所做的功W.W=|F||s|cosθ.

在这里功W就是今天学习的数量积F·s.

在完成平面向量数量积的数学抽象之后，再来看平面向量数量积的物理背景，学生对“功”的理解必然得到深化，也显现了数学的内在力量.

3.10 关于运算律

在3.7已经指出数量积是一个对称的二元函数，而不是向量的运算.既然不是运算，当然也就不存在运算律.是函数应该有的是函数的性质，按照北大丘维声教授的观点，数量积具有正定性、对称性和双线性性，即：a·a=|a|2≥ 0，当且仅当a=0时“=”号成立；a·b=b·a；a·(b+c) =a·b+a·c；

a·(kb) =ka·b.应该是理所当然的.

3 结语

对数学的理解是一个长期、艰难、反复、不可穷尽的过程，但理解数学是教好数学的前提[注]数学通报 2015年第54卷第1期章建跃《理解数学是教好数学的前提》.从数学知识的发生发展过程角度分析面向教学的数学知识，从内蕴于数学知识中的认识视角、思想与方法等角度全面解析数学课程内容，由此生发教育上的见解并付之于数学教育的实践，是一条很好的自我修炼的途径.在此基础上，才能更好地“理解学生”、“理解教学”，从而更好地培育学生的数学核心素养.