课本例题的理解与教学①
渠东剑
(南京市秦淮区教师发展中心 南京市高中数学渠东剑工作室 210002)
课本,一定意义下是课程标准的具体化,是教师教、学生学的最权威媒体,是教学研究、教学评价与各类考试命题的重要依据.课本的编写,是众多专家智慧的结晶,并经过了教学实践的检验,而不断优化与发展起来的.在教学实践中,课本理应得到高度重视.如果说教学要“用教材教,而不是教教材”,那么首先要“用”课本,用好课本,而用好课本的前提是理解课本,尊重课本.
例题,是数学课本的重要组成部分;例题教学,是数学教学的重要内容.按现代汉语词曲,例,用来帮助说明或证明某种情况或说法的事物.数学课本例题,则是以题目(含解题过程)的形式,进一步诠释教学内容、深化知识应用与理解、突出分析问题与解决问题的过程与方法、示范解题过程的书写.课本例题具有基础性、典型性与发展性:例题往往是初学知识的“第一次”应用,是解决相关问题的开始,故一般难度不大,适宜学生学习;在寸土寸金的课本中,例题占有一席之地,其选择一定是精挑细选的、典型的与必要的,随后的练习题等大都有例题的影子,让学生的解题从模仿开始,一定意义下、一定程度地降低了客观存在的学习难度;课本例题一般具有丰富的内涵,因而具有发展性,例如,一些例题常被称作“母题”,由此变式引申拓展,去解决一类问题,几乎每一套高考试卷,均有较大数量的题目来自课本例、习题的组合、改编,绝大多数题目都可以在课本例题中找到它的影子.所以,高度重视、深刻理解、认真研究课本例题,并在实践中努力教好课本例题,是数学教学的必然要求.重视课本必须重视课本例题,用课本教就要用好课本例题;重视课本例题就是重视课本,就是在“用课本教”.
然而,环顾当下的高中数学教学,不重视课本、甚至远离课本已成为普遍现象.无论是新授课教学,还是高考复习教学,一些教师对课本例题不屑一顾,认为其“基本”、“平常”、“单调”,对课本例题教学敷衍了事,甚至置之不理.尤其是时下导学案教学风靡一时,愈演愈烈,其中可能出现了背离教学规律的现象:教学设计服从于解题教学,解题教学追求题型模式,题型模式追求“高、大、上”——忽视学生学习的基本现实,肆意拔高教学要求,执意强调题型全面,变式与拓展脱离实际,使学生的学习无法落地生根,……学生的学习深一脚浅一脚,教师的教学失去了定盘星.
有鉴于此,笔者选择苏教版教材上的一些典型例题为例,试图去理解题目内涵,揣摩编者用意,挖掘题目价值,探索教学实践,……思考例题教学的应有之义,以期抛砖引玉,使课本例题的教学回到其应有的、重要的位置上来.
1 从学生认知视角理解课本例题
苏教版必修1—1第三章“导数及其应用”,第3.3节“导数在研究函数中的应用”.在3.3.1 “单调性”中,给出“导数与单调性的关系”的结论之后就是例题1:
确定函数f(x)=x2-4x+3在哪个区间内是增函数,哪个区间内是减函数;
在3.3.2“最大值与最小值”中,给出“求最大值与最小值的步骤”之后,接下来就是例题,其中第1道题是:
求函数f(x)=x2-4x+3在区间[-1,4]上的最大值与最小值.
这两道例题所研究的对象,是学生再熟悉不过的二次函数,所要解决的问题(单调性、最大值与最小值)早已为学生所掌握,而且从初中到高中不止一次地研究过,可以说这两道题所要研究的问题,对学生而言是已经解决的问题,似乎在这里再出现已无必要.正因为如此,一些教师、甚至一些学生对此有所不屑,教学要么一带而过,要么弃之不用.然而,将题目放在例1的位置,明明是要突出其重要性的.那么,编者为什么要这样安排呢?
其实,这要从学生认知发展的角度去理解.学生刚刚学习的新知识,其认识是肤浅的,认知结构是不稳固的,尚缺乏心理认可.特别是,这里的单调性、最大值与最小值问题,研究的方法变了,结论的形式是新的.面对新旧认知的矛盾与冲突,学生难免会产生一些疑惑.例如,此单调性与彼单调性、此最值与彼最值相同吗?若相同,为何对已研究过的问题还要重新研究?这里的结论可信吗?……按建构主义理论,学生学习建构新知识,要基于已有认知结构,打破已有的认知结构,将新知识纳入到已有的认知结构中去.具体到这里,就需要打通单调性与最值新旧知识之间的联系,用已有的知识去理解新知识,并建立新旧知识间的联系,实现认知的发展.此时,借用学生所熟悉的简单的二次函数作为载体,用刚刚得到的结论去研究其单调性与最值,自然会与原有的认知相互印证,从而达到心理认可,产生积极的学习效果.
因此,用联系的观点、比较的方法去教好这两道“简单题”,让学生“起好步”,是必要的、不可跳过的一步.如果我们借口题目简单,且属于已经解决了的问题,将其舍弃,直接进入较为复杂的例题教学,例如,选择一些非用导数不能解决单调性或最值问题的函数,则可能打破认知的连续性,违反了循序渐进的认知规律.
当然,基于这样的认知起点,实现认知的循序渐进,还在于认知的深化与发展.例如,课本紧接着上面的两例,各自给出相应的例2,对象为三次函数,即分别研究三次函数的单调性与最值问题.而三次函数就没有了上述已有的认知基础,相对学生而言是陌生的,相对于问题的解决,已有的知识与方法不能解决新的问题了,怎么办?矛盾的冲突自然开启“非用导数不可”的话题.而这个新的方法则是刚刚学过的、为已有认知所检验过的、深信不疑的.这正是认知的自然发展、学习新知识的动力所在.从这一点看,编者这样的安排,由浅入深,自然而然,确是匠心独运的了.
2 从整体结构视角理解课本例题
苏教版必修4第一章“三角函数”第1.4节“三角函数的应用”,课本给出2道例题和一个探究案例,其中例2是:
一半径为3m的水轮如图1所示,水轮圆心O距离水面2m,已知水轮每分钟转动4圈,如果当水轮上点P从水中浮现时(图中点P0)开始计算时间.
(1)将点P距离水面的高度z(m)表示为时间t(s)的函数;
(2)点P第一次到达最高点大约要多长时间?

图1
按照本节标题分析该例题的教学,似乎主要是体现“三角函数的应用”,具体地,就是正弦型函数y=Asin(ωx+φ)的应用,教学也应围绕如何“用”知识解决实际问题去展开.其实不尽然.
首先,函数y=Asin(ωx+φ)是描述较为复杂周期现象的数学模型:从函数关系分析,可以认为是由正弦函数、一次函数复合而成的函数;从几何背景观察,相对于点(cosα,sinα)刻画单位圆上质点的匀速运动(角速度为1,从点A(1,0)出发)而言,可以刻画更为一般的圆周运动(半径A≠1,角速度ω≠1,可以从一般位置出发);从生活背景理解,富有丰富的现实意义,例如刻画潮汐现象的函数y=Asin(ωx+φ)+K,其中的A,ω,φ,K都有明确的现实意义.因此,研究函数y=Asin(ωx+φ)的性质,自然要明白它的来龙去脉.
其次,围绕函数y=Asin(ωx+φ)知识的发展线索,我们整体把握课本组织结构:以“摩天轮情境”引入课题,建立三角函数的概念,在研究函数y=sinx,y=cosx的图象与性质时,偶有涉及正弦型函数,主要是“五点法”作图、换元法求其单调区间与最值,等;尔后,专门用一节的篇幅研究了函数y=Asin(ωx+φ)的图象与性质,不过用“告知”的方式交代了该函数的生活、物理与工程等背景,故而这个函数怎么来的,为什么会是这种形式,似乎还缺乏应补的一课.
第三,从课程标准“内容与要求”分析.课程标准相关“内容与要求”是:“结合具体事例,了解y=Asin(ωx+φ)的实际意义……会用三角函数解决一些简单实际问题,体会三角函数是周期现象的重要函数模型.”笔者认为,具体到该例题的教学,应从以下几个方面去把握:例题教学就是“结合具体事例”的绝好机会,而且就整体把握教材而言是最后的机会了;问题的解决过程,正是“用三角函数解决一些简单实际问题”的过程;例题的教学过程,既是用三角函数解决实际问题,是在教学生“会用……”,又是通过解决问题的建模过程,达到 “结合具体事例,了解……”的目的.学习数学模型的最好方法是亲身经历建立模型的过程,让学生从实际背景出发,将实际问题抽象为数学问题,并围绕数学问题的解决,去经历一系列探究活动过程:怎样想到建立坐标系的,如何建立坐标系,并联系回顾周期概念……就显得十分重要.至于三角函数的应用,自然融合在上述过程中了.
第四,立足于学生能力的发展,该例题的教学,必然要突出建立数学模型的全过程,体现解决现实问题的一般方法,促进学生分析问题与解决问题的提高.即从审题开始,将现实问题抽象为数学问题,建立数学模型,解决数学问题(数学模型),回应回答现实问题.这样的过程,既要让学生亲历亲为,又要在“小结与拓展”阶段,启发引导学生去感悟、总结,以期达到对知识的再回顾,对函数y=Asin(ωx+φ)的再建构,对研究方法认识的再深化.
基于上述分析,我们对该例题的教学就不那么茫然、轻率了.相反,该例题的教学要承载更多的内涵,教学具有挑战性,也将大有可为.
3 从思想方法视角理解课本例题
苏教版必修5第三章“不等式”第3.2节“一元二次不等式”,课本首先以具体的一元二次不等式的例子,利用数形结合方法,借助于一元二次函数图象,探究出解一元二次不等式的一般步骤:第一步,解方程;第二步,画出抛物线的草图;第三步,观察图象,得不等式的解集.紧随其后,给出例1:
解下列不等式:
(1)x2-7x+12>0; (2)-x2-2x+3≥0;
(3)x2-2x+1<0; (4)x2-2x+2>0 .
其后的解题示范过程就是重复上述的解一元二次不等式的步骤.
这组不等式是较为简单的,也是学生所熟悉的.虽然此前没有课本相关章节去专题解决这类问题,但是,就求解这类不等式问题来说,学生可能并无困难.他们在“二次函数”、“集合”、“函数”等有关内容学习过程中,已多次遇到这类不等式,也掌握了因式分解、画图象观察等解题方法.那么,怎样认识这些简单的问题出现在这里,特别是在第一个例题的位置,且其解法一成不变地重复上述步骤呢?
首先,这几个问题虽然简单,但类型各异:二次项系数有正有负,不等号有大于(大于或等于)有小于,其判别式有正有负……但其解法都可以利用本课伊始探究的一般步骤.因而这个一般步骤具有一般的“算法”的特点,具有较强的可操作性,是学生应该掌握的.
其次,更为重要的,该解题步骤突出了函数、方程与不等式的数学思想:解不等式——解方程——画函数图象,这分明是将不等式的研究统一到函数的大背景下,即将不等式、函数与方程联系起来、统一起来,进而用函数统领函数、方程与不等式研究全局.这正是中学数学的核心知识、观点与方法.
再次,问题解决的过程蕴含了丰富的数学思想方法:函数、方程与不等式、化归与转化、数形结合、分类讨论,等.看似简单,实则寓意深远.
具体到这几道问题的解决,也许上述三个步骤与因式分解相比没有多大优势,一成不变地强调三个步骤没有太多意义,但从课本的整体结构把握,尤其是突出函数这一大观点、大方法去考虑,也许结论就是相反的了.因此在这里,突出解不等式的三个步骤,并一以贯之地执行,既是问题解决自身的需要,更是突出核心观点方法的必然,还有着眼于知识发展的眼光——当后面遇到含有参数的一元二次不等式问题,特别是需要多层级分类讨论的问题时,将更加凸显函数思想方法的优越性,甚至是不二的选择.
4 从解题示范视角理解课本例题
苏教版必修2第一章“立体几何初步”第1.2.2节“空间两直线的位置关系”,在公理4后给出例1及其证明过程:
如图2,在长方体ABCD-A1B1C1D1中,已知E,F分别是AB,BC的中点,求证:
EF∥A1C1.
证明:连结AC,在△ABC中,因为E,F分别是AB,BC的中点,所以EF∥AC.
又因为AA1BB1,BB1CC1,所以AA1CC1,
从而四边形AA1C1C是平行四边形,所以AC∥A1C1.
从而EF∥A1C1.
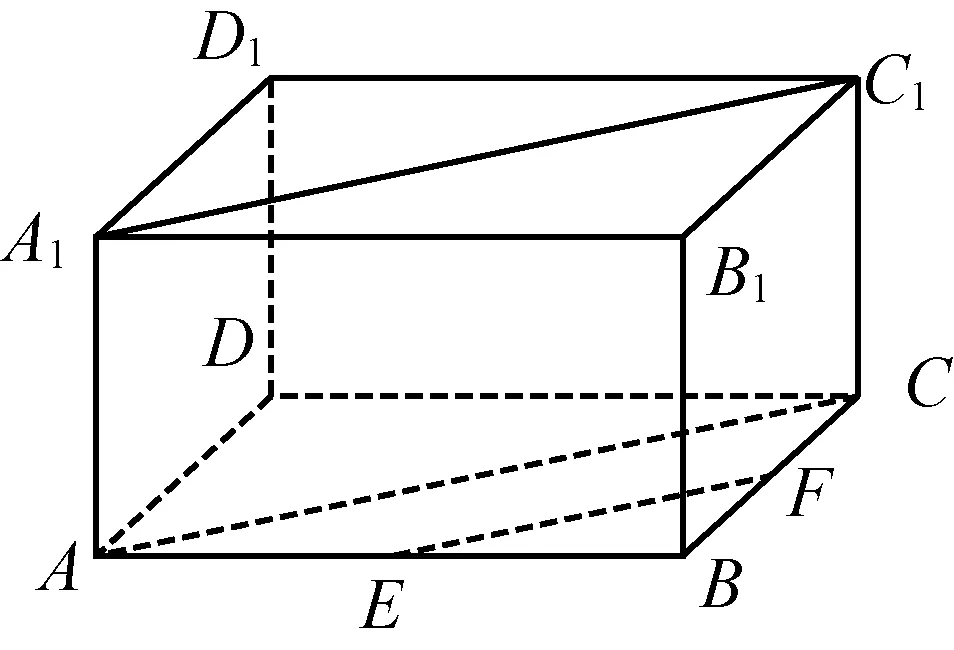
图2
一些教师认为,该题非常简单:图形直观,位置关系清楚,推理过程简单,学生学习没有困难,故在教学中不愿着力,甚至对该例题置之不理.这是没有深刻理解题目的表现.
笔者认为,该例题意在做出两个示范:一是用演绎推理方法去证明立体几何问题,展示严密的逻辑推理链条,体现推理方法,明确哪些是条件,哪些是结论,从条件推得结论有何依据;二是规范的书写表达过程,即将每一个推理的逻辑段串连而成逻辑链,处在中间位置的,既是上一个逻辑段的结论,又是下一个逻辑段的条件,推理步步有据,环环相扣.须知,这是苏教版“立体几何初步”例题中的第一道证明题,对引导学生执果索因,寻找推理的源头,用数学符号语言规范表达交流,重视演绎推理,学习理性精神,形成实事求是的科学态度,无疑具有积极的、重要的意义.
联想这些年高考数学江苏卷阅卷情况,对学生的书写表达有较高的要求,特别是立体几何证明问题,要求学生必须思路清楚、推理严谨、表达规范.一些教师在高三复习教学时,比较重视学生的书写表达,立体几何证明题尤甚.但学生的答卷却不能令人满意.究其原因,可能与平时教学没有落实到位有关.例如,在本例题中,虽然AA1CC1是显而易见的,但却是不能直接利用的现成结论,需要根据长方体的性质,应用公理4去论证.因此,在本题教学过程中,要让学生经历并体会一般的解题过程:怎样分析问题,已知什么,要证什么;而要完成这样的证明,又要做什么;明确哪些是条件,哪些是结论,由条件推得结论的依据在哪里,为什么;怎样用数学语言规范表达……
5 从知识发展视角理解课本例题
苏教版必修4第二章“平面向量”第2.2.3节“向量的数乘”,先以例题形式给出“三角形中位线定理”背景下的向量共线问题情境,然后给出向量共线定理及其证明,紧接着呈现了如下例题:
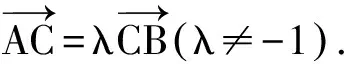


图3
这是一道内涵丰富、联系广泛、生长潜力巨大的题目.教学不应该就题论题,可以视学情允许,关注后续课程发展,适时进行可能的探究学习.要充分挖掘该题的价值,突出知识联系与发展,提高学生思维能力.这里,仅就知识层面,给出该题的拓展与可能的探究方向.

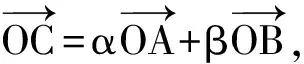


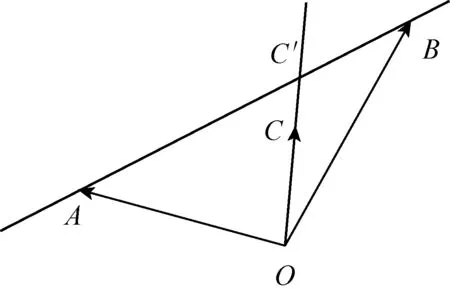
图4

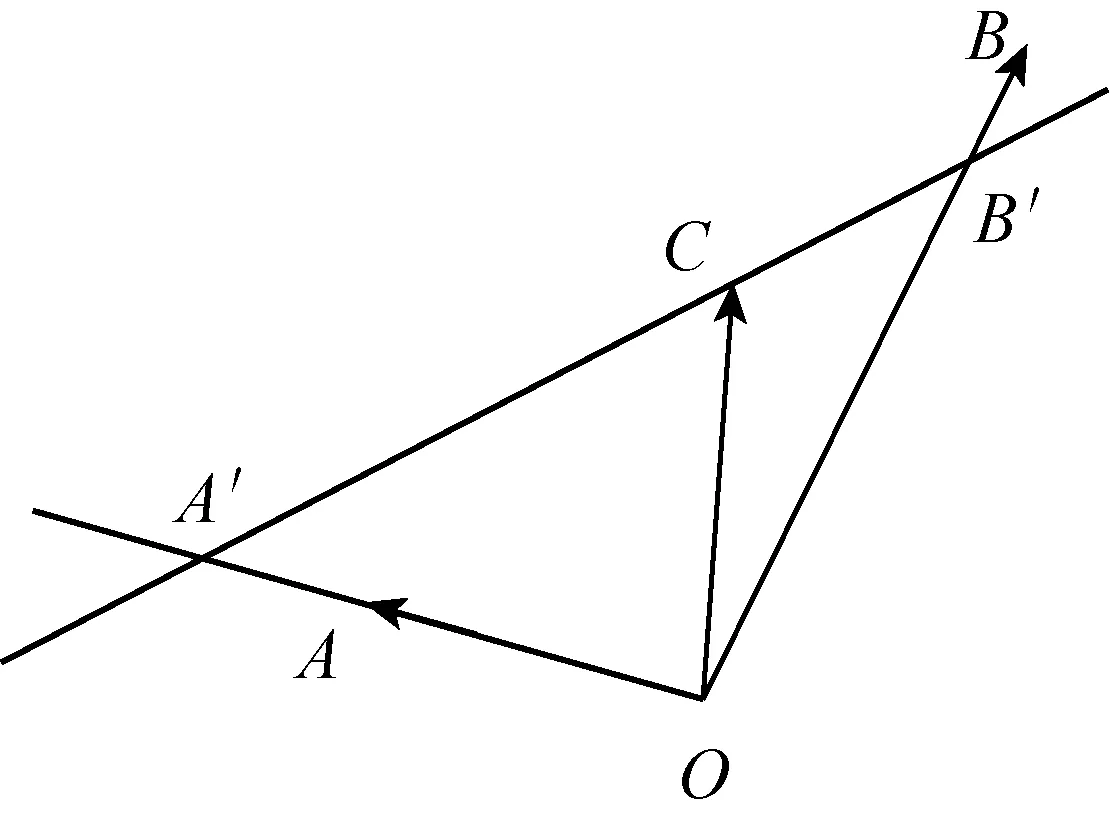
图5
(5)定比分点公式.该结论实际上是向量形式的定比分点公式,若在随后学习向量的坐标表示时,以坐标代入,即可得到坐标形式的定比分点公式


总之,课本例题蕴含着丰富的宝藏,需要我们去开发.用好课本例题的前提在于读懂例题;读懂例题需要从多个视角,立足于教材的整体把握,着眼于学生的长远发展利益.在读懂课本例题的基础上,创造性地设计适合的、属于自己的、属于所教学生的教材.“没有最好,只有更好.”让我们一道努力探索下去.

