用几何画板探究四边形中的Morgan问题

陈咸存

(宁波教育学院 315010)

1 引言

关于三角形内某一图形面积与原三角形面积之比问题已引起很多人的关注[1]-[5]，如文[1]得到Marion定理:

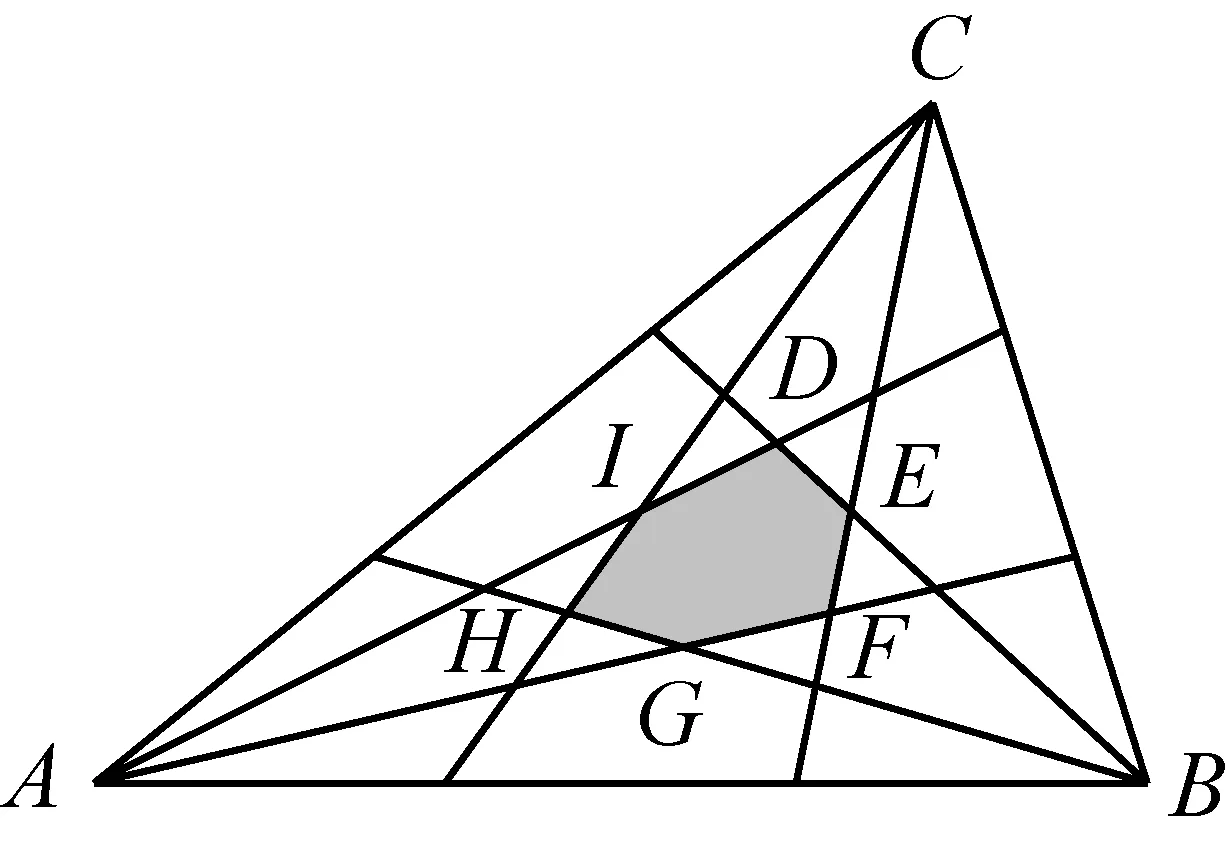
图1

定理1如图1，在△ABC中，将每边三等分，则等分点与对顶连线得到的六边形

九年级学生Morgan[2]利用数学软件几何画板将Marion定理推广得到Morgan定理：

图2

考虑到几何画板中变换之一缩放，文[5]用几何画板将Morgan定理由奇数推广到实数情形：

更一般地有：

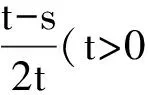
定理3-4考虑了由Morgan定理或Morgan定理衍生出来涉及三角形内某一图形面积与原三角形面积的比值问题，不妨称为三角形中的Morgan问题.那么四边形中是否也有类似的结论成立?熟知三点简比(缩放可看成三点简比)、两图形面积之比是仿射不变量，而三角形与平行四边形是仿射不变图形.因而Morgan问题很容易推广到平行四边形情形.下面分别对平行四边形及任意四边形探讨Morgan问题.

2 平行四边形

文[6]得到：

图3

一般地可证：

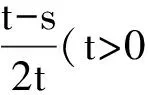
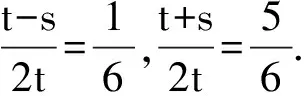
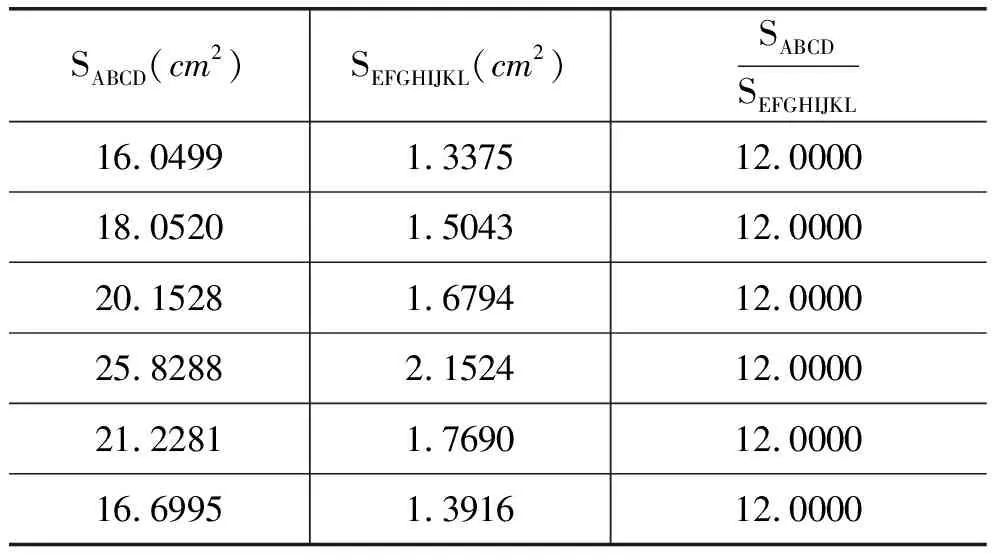
表1

3 任意四边形

3.1 猜想与验证

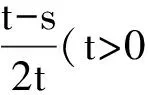
图4

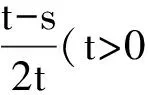
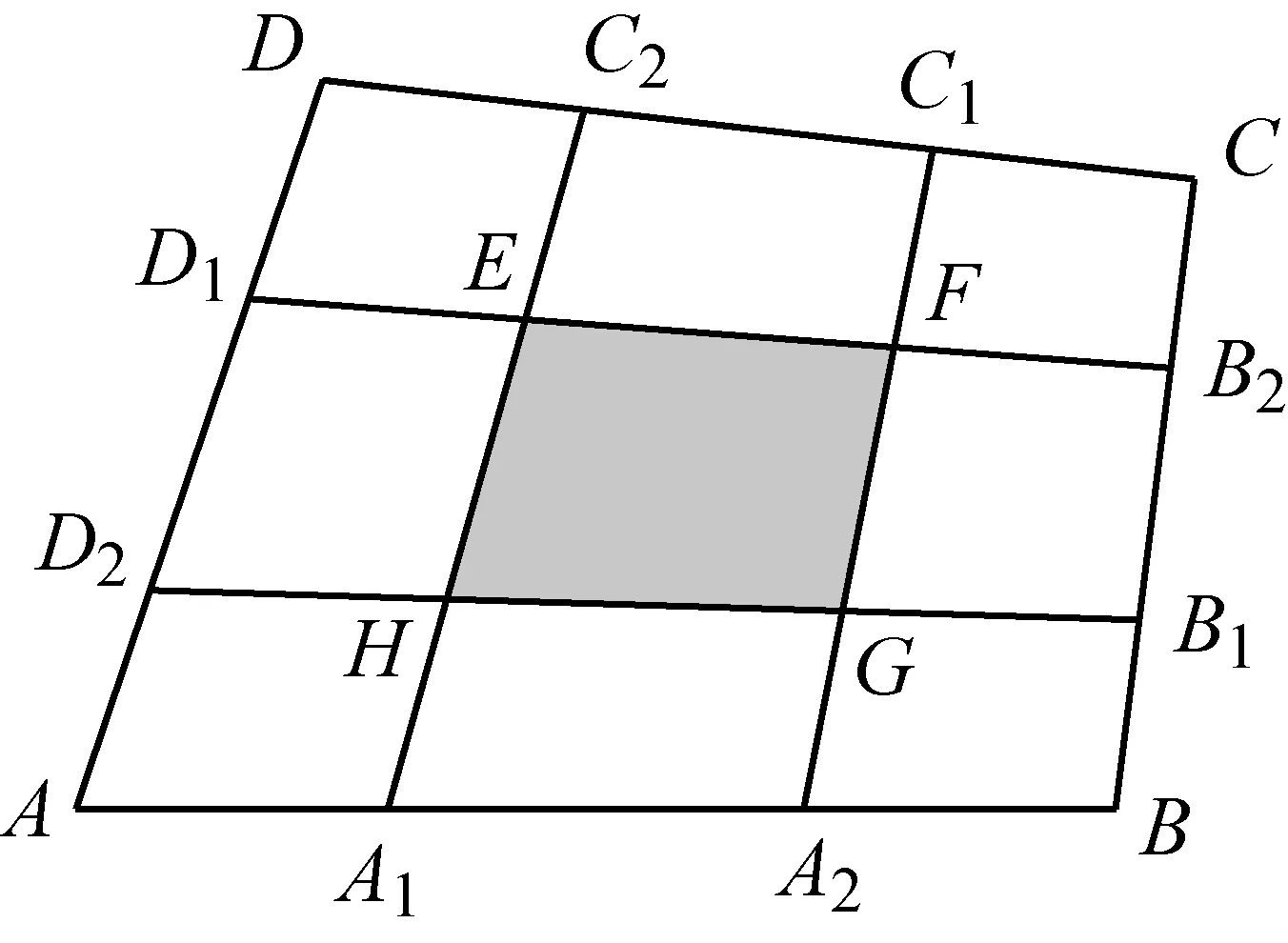
图5

表2

3.2 证明

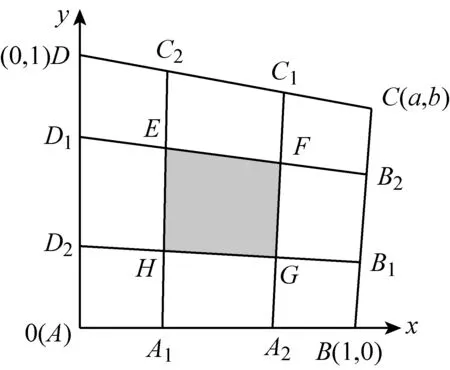
图6

下证用另一方法证明定理7，先证下面结论：

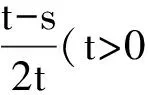
证明设AB=a，CD=b，则有

当AB与CD平行时，不妨设AB与CD间距离为h，

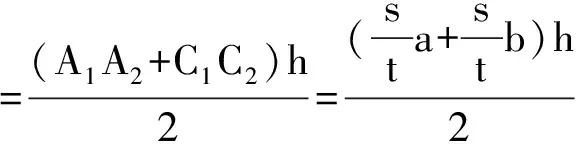
当AB与CD不平行时，不妨设P=AB×CD，

如图7.令BP=m，CP=n，∠APD=θ，

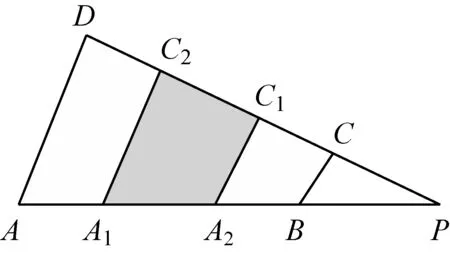
图7

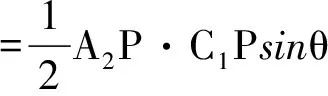
有SA1A2C1C2=S△A1PC2-S△A2PC1

故定理8得证.