马鞍面与一类轨迹问题

平光宇 龚卫东

(广东省深圳市高级中学 518040)

笔者在教学中遇到一道轨迹问题，经过师生一起探索，发现背后隐藏着空间解析几何中的典型曲面：双曲抛物面(也叫马鞍面，以下称马鞍面)，再返回到问题中来，编出了一系列的立体几何与解析几何完美结合的新颖问题.

例(如图1)在正方体ABCD-A1B1C1D1的棱上有几个点到异面直线a、b(图中加粗的两条线，以下同此)的距离相等？

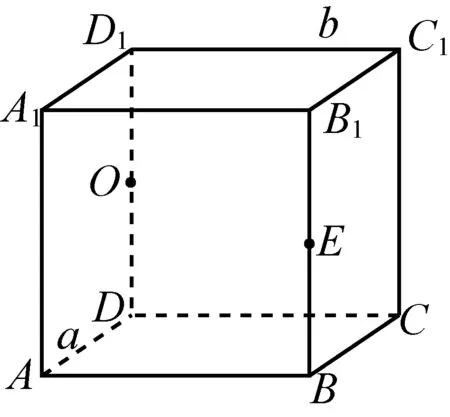
图1

答案很简单，满足条件的点有四个，分别是点O、A1、E、C(其中，点O、E分别是棱DD1和BB1的中点).

有学生问：在正方体的表面上到直线a、b的距离相等的点还有哪些？能画出轨迹吗？

另一个学生问：在正方体的表面及其内部到直线a、b的距离相等的动点的轨迹是什么？再进一步，在空间到直线a、b的距离相等的动点的轨迹是什么？

笔者意识到这是一个非常值得探究的问题，于是回答道：不知道，但这显然是个好问题，值得探究. 并表扬了这两位同学善于思考、质疑并能提出有质量的问题. 然后我要求数学课外小组的同学和我一起探索.同学们异常兴奋，表现出了极大的学习兴趣. 经过一段较长时间师生共同努力，反复尝试，查阅资料，推导与论证等，最终形成以下结果.

1 空间到异面直线a、b的距离相等的动点的轨迹是马鞍面

若异面直线a、b相互垂直，设它们之间的距离是m，设DD1是它们的公垂线段，则DD1=m,如图2. 构造正方体ABCD-A1B1C1D1. 设AA1、CC1的中点分别是H、K，以DD1的中点O为原点，OH为x轴，OK为y轴，OD1为z轴建立空间直角坐标系O-xyz. 设点P(x,y,z)是轨迹上任意一点，作PQ⊥平面ABCD, 垂足是Q，作PR⊥平面A1B1C1D1, 垂足是R，又作PM⊥a,PN⊥b, 垂足分别是点M、N，连接QM、RN, 则QM⊥a,RN⊥b. 所以

图2

由PM=PN,

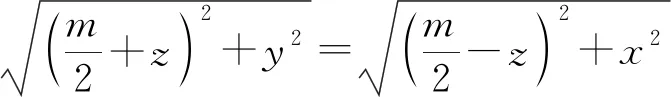
化简得方程：x2-y2=2mz

①

对于任意两条异面直线a、b，设它们所成的角是2α(0° <α≤45° ), 它们之间的距离是m，设它们的公垂线段是ST，则ST=m, 如图3. 取ST的中点O，过点O分别作直线a′,b′，使得a′∥a,b′∥b, 以点O为原点，分别以相交直线a′，b′(所在平面内)所成四个角的两条角平分线为x轴、y轴，以直线ST为z轴，建立空间直角坐标系O-xyz(为达到直观的效果，以点O为中心，分别以异面直线a、b为上下底面的两条对角线所在直线，构造长方体ABCD-A1B1C1D1)如图3. 设点P(x,y,z)是轨迹上任意一点，作PQ⊥平面ABCD, 垂足是Q，作PR⊥平面A1B1C1D1, 垂足是R，又作PM⊥b,PN⊥a, 垂足分别是点M、N，连接QM、RN, 则QM⊥b,RN⊥a. 取BC的中点E.

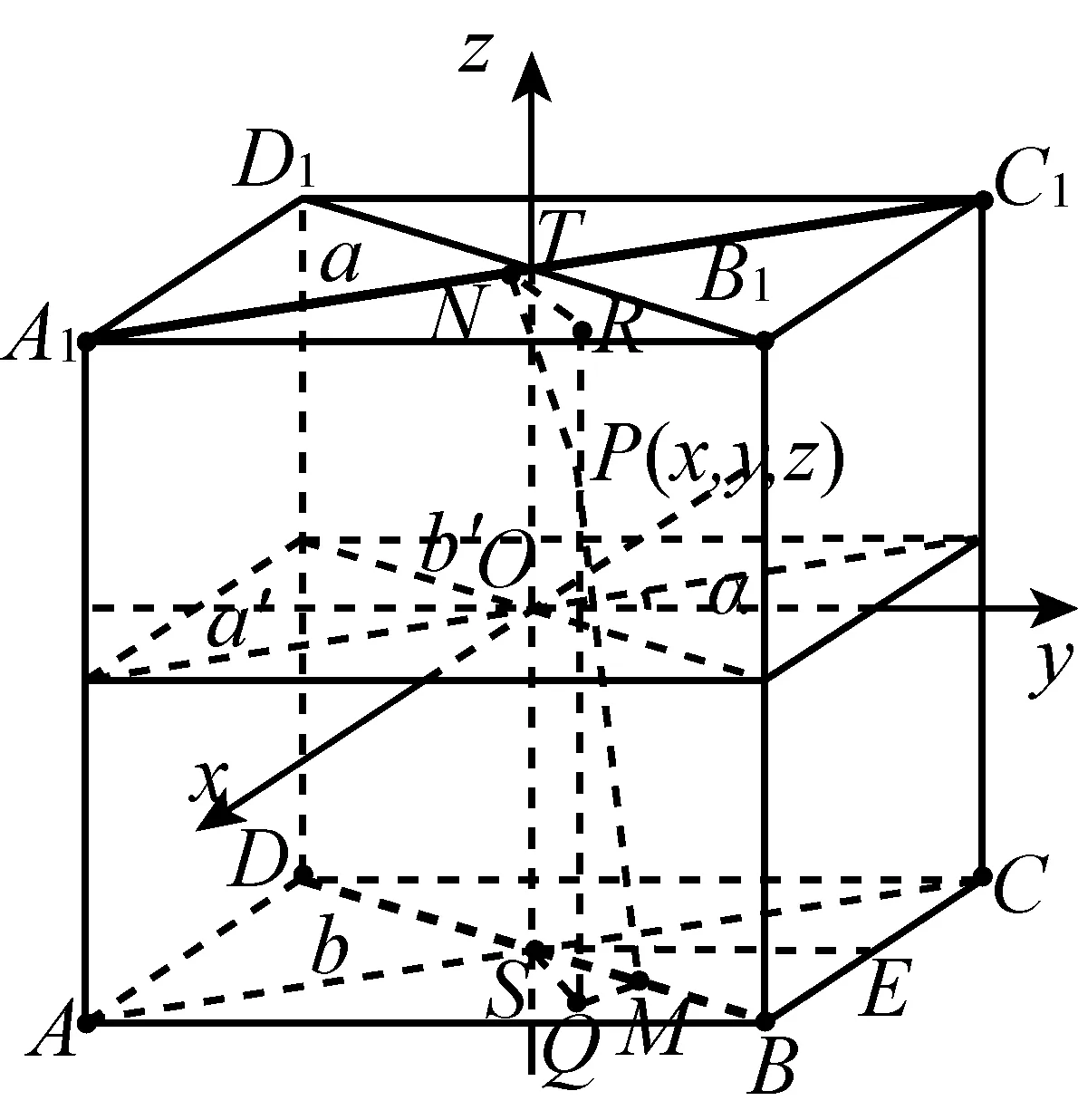
图3

sin ∠QSM=sin |∠QSE-∠MSE|

=|sin (∠QSE-∠MSE)|

=|sin ∠QSEcos ∠MSE

-cos ∠QSEsin ∠MSE|

所以，QM=SQ·sin ∠QSM

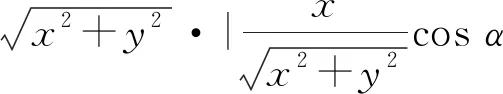
同理RN=|xcosα+ysinα|.

由PM=PN，

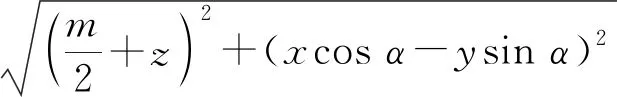
②

方程①和②均表示马鞍面.由此可得：

定理到两条异面直线的距离相等的动点的轨迹是马鞍面(由方程的形式可知，此轨迹只是一类特殊的马鞍面，不是所有的马鞍面)[1].

2 根据方程，画出马鞍面

方程①是一个三元二次方程，我们能根据方程画出轨迹吗？这在过去是不可能的，只能在教科书中翻出一些示意图，然而利用现代信息技术我们自己也可以画出其轨迹，几何画板没有设置空间直角坐标系，因此不能直接根据三元二次方程画出空间曲面. 笔者经过一番探索发现，几何画板可以在坐标系里以动点为原点建立新的坐标系，这样，用“动态坐标系”画出了方程①的曲面.具体如下：

把x看成一个可变的常数t，则方程①就转化为关于x，z的二元二次方程. 从中解出z来，得到函数

取动点O′(t, 0, 0), 以动点O′为新原点，在经过点O′垂直于x轴的平面内建立新坐标系y′O′z′.相当于把原坐标系按向量OO′平移到平面y′O′z′. 在新坐标系中画出该函数的曲线(如图4).

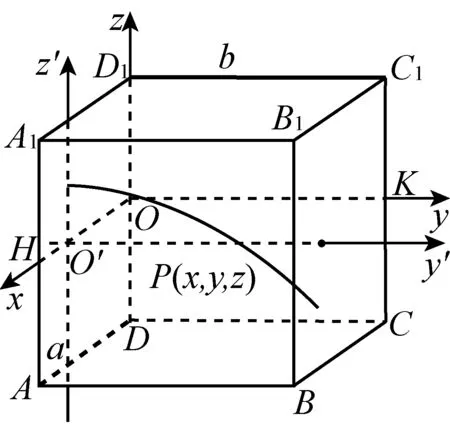
图4

改变t的值，就可以构造出曲线束，以曲线束表示曲面，如图5. 此即所求点P的轨迹，即马鞍面. 并且，图5把马鞍面与正方体表面的交线也显示了出来,四段交线均是抛物线的一部分. 不过图5只是马鞍面的一部分.马鞍面的整体形象如图6.

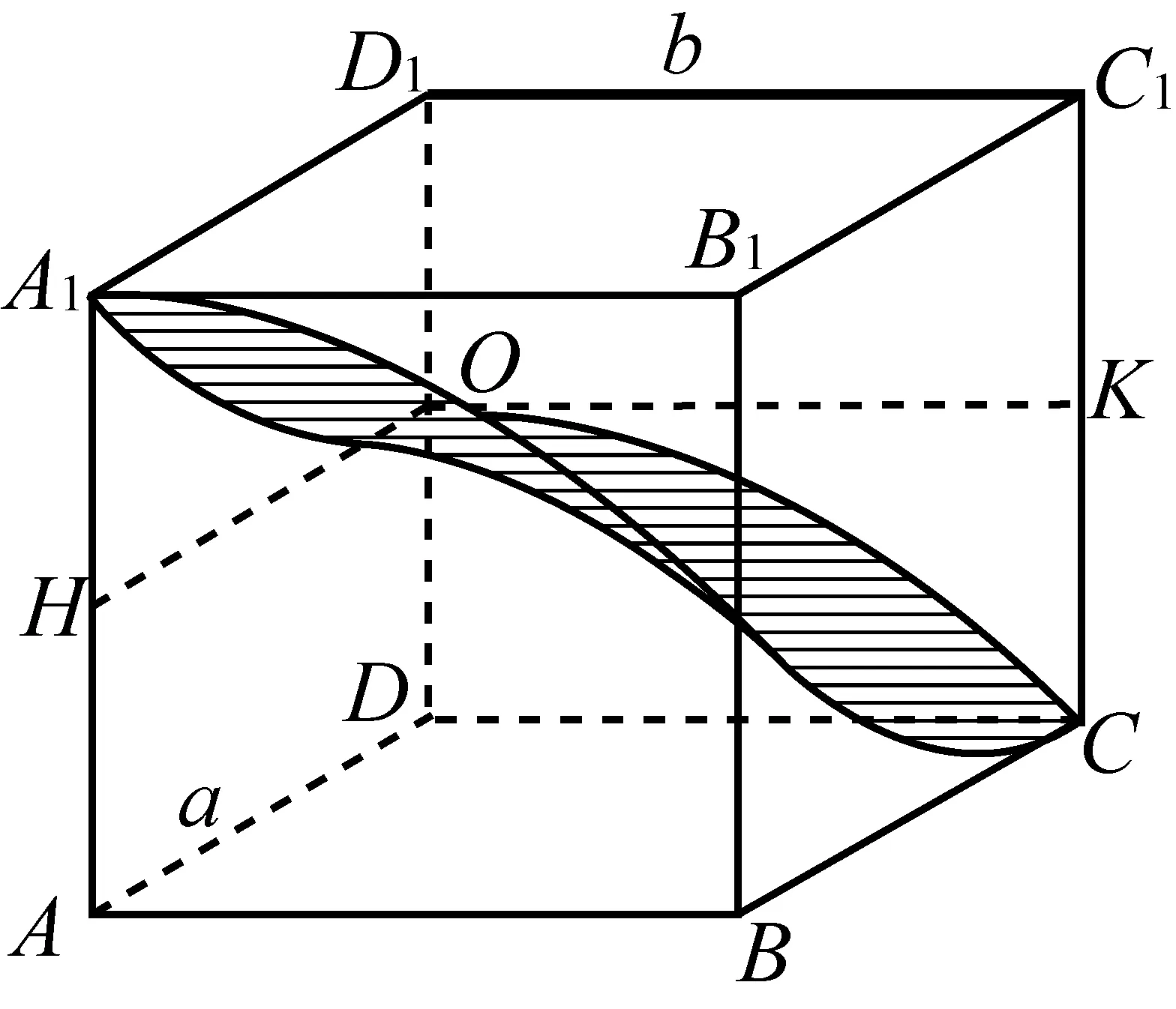
图5

图6

用几何画板画出方程②的轨迹(过程略)，可以看出马鞍面是“双直纹”面, 如图7.

图7

3 马鞍面的性质

由方程①和②可知马鞍面具有以下两条性质.

性质1用平行于异面直线a,b的公垂线或者经过该公垂线的平面截马鞍面，截线都是抛物线或者一条直线(马鞍面的一条直纹)；

性质2用和异面直线a、b的公垂线相交的平面截马鞍面，截线都是双曲线或者两条相交直线(马鞍面的双直纹).

此两条性质的证明比较复杂，属于空间解析几何研究的内容.本文从略[2].

4 居高临下，编出新题

既然到两条的异面直线a,b的距离相等的动点的轨迹是马鞍面，而马鞍面又具备上面两条性质，那么，我们可以得出以下结论：在图1的正方体的每个面或者对角面所在的平面内，到异面直线a,b的距离相等的动点的轨迹就相当于用该平面去截马鞍面所得到的曲线，则一定是抛物线、双曲线、两条相交直线或者一条直线这四种情况之一.

这样我们就可以回到图1或者再构造新的图形，编出一系列相关的题目：

变式1如图1，在正方体ABCD-A1B1C1D1的面DCC1D1内到异面直线a、b的距离相等的动点的轨迹是( ).

A.圆弧 B.椭圆的一部分

C.双曲线的一部分 D.抛物线的一部分

答案：D(如图5，轨迹是马鞍面与正方形DCC1D1的交线，即正方形DCC1D1内点O,C间的一段抛物线).

说明：此题资料上常有.用抛物线的定义即可解决.另外也可以把面DCC1D1改为面ADD1A1，难度相当，答案即为图5中正方体左侧面内的O、A1两点间的一段抛物线.

变式2如图1，在棱长为2的正方体ABCD-

A1B1C1D1的面ABB1A1内到异面直线a、b的距离相等的动点的轨迹是( ).

A.圆弧 B.椭圆的一部分

C.双曲线的一部分 D.抛物线的一部分

解以直线AB为x轴，直线AA1为y轴，在平面ABB1A1内建立平面直角坐标系(如图8)，设点P(x,y)是轨迹上任一点，由PM=PA，可得

图8

化简得轨迹方程为x2=-4(y-2)(0≤x≤2).

答案：D(如图8，抛物线的一部分).

点评：在多面体的某一个面上建立坐标系，是本题的难点，也是下面所有题的难点.同时也是这一系列题的一个特色.

说明：也可以把面ABB1A1改为面BCC1B1,如图9. 问题的解答思路和答案是一样的，但方位不同, 建坐标系的难度有所增加.可以直线BC为x轴，直线BB1为y轴建立平面直角坐标系, 求得轨迹方程是(x-2)2=4y(0≤x≤2).轨迹也是抛物线的一部分.

图9

变式3如图10，已知长方体ABCD-A1B1C1D1的长、宽、高分别是2、1、2，则正方形ABB1A1内到异面直线a、b(即直线AA1、DC)的距离相等的动点的轨迹是( ).

图10

A.圆弧 B.椭圆的一部分

C.双曲线的一部分 D.抛物线的一部分

图11

变式4如图12，已知长方体ABCD-A1B1C1D1的长、宽、高分别是2、2、1，则正方形A1B1C1D1内到异面直线a、b的距离相等的动点的轨迹是( ).

A.圆弧 B.椭圆的一部分

C.双曲线的一部分 D.抛物线的一部分

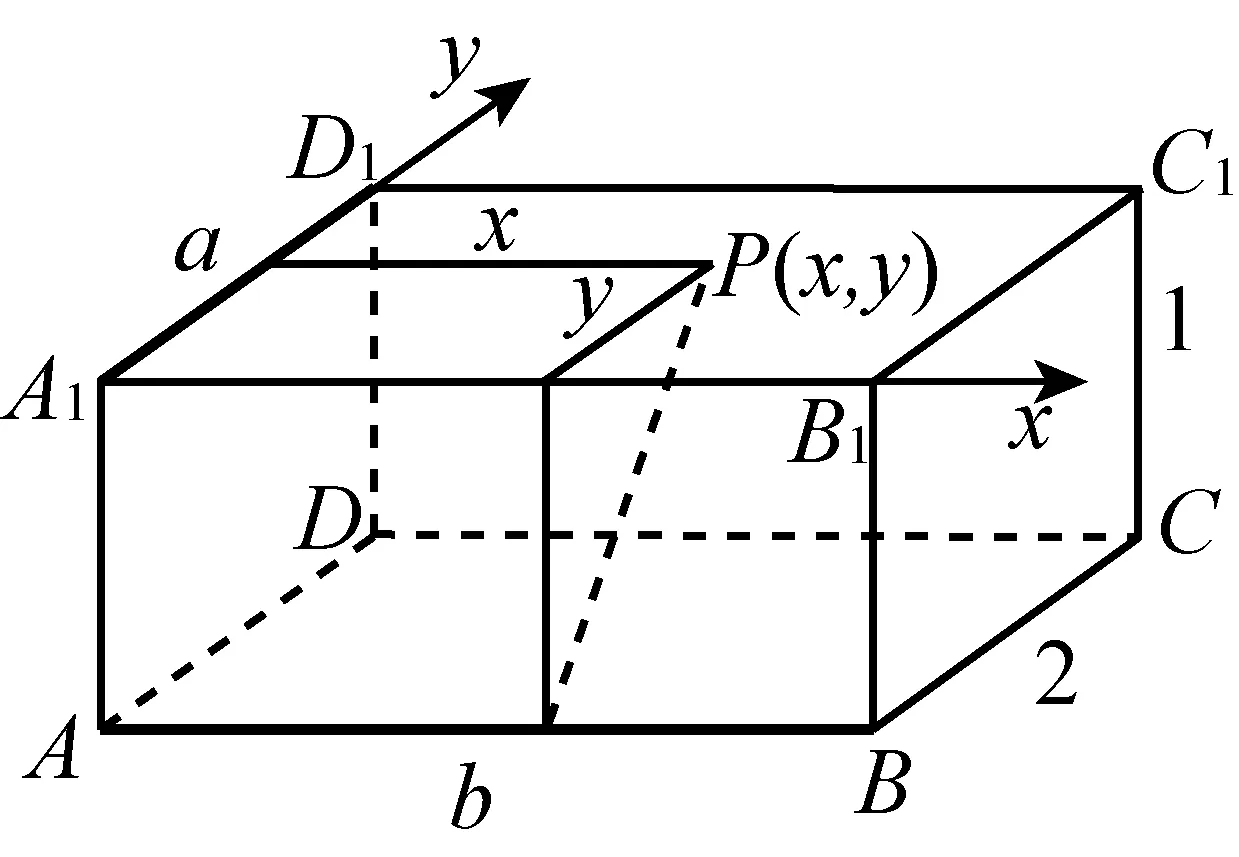
图12

提示：此题相当于把上题的“立着的箱子”放倒，可如图建立坐标系(坐标平面是水平放置的直观图).求得轨迹方程是x2-y2=1(0≤x≤2，y≥0).故选C.

变式5如图13，在棱长为2的正方体ABCD-

A1B1C1D1的对角面DBB1D1内到异面直线a、b的距离相等的动点的轨迹是( ).

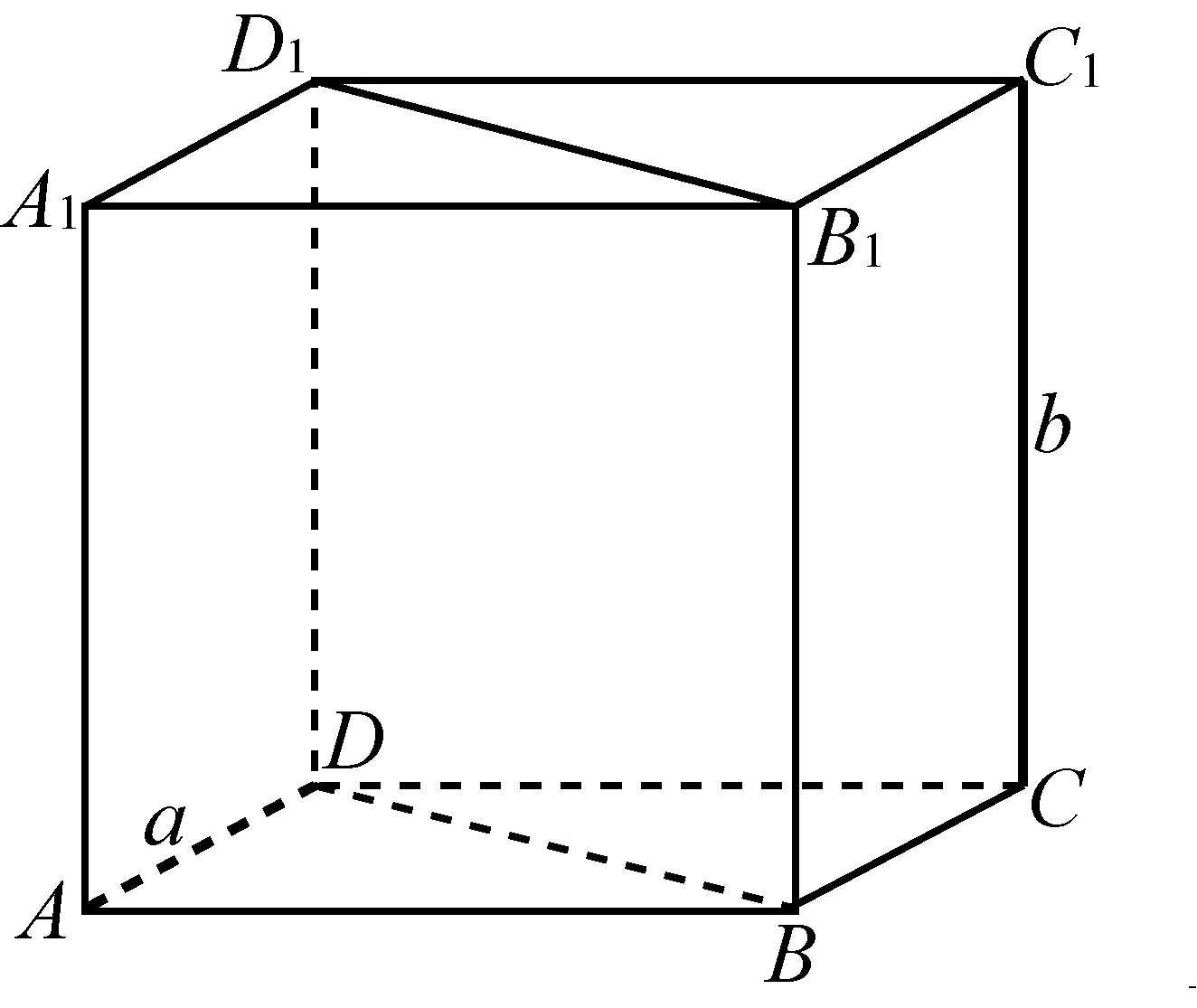
图13

A.线段 B.圆弧

C.双曲线的一部分 D.抛物线的一部分

解法1如图14，以DB为x轴，DD1为y轴，在平面DBB1D1内建立平面直角坐标系. 设点P(x,y)是对角面内任意一点，如图14作辅助线，DQ=x,QP=y. 由PR=PT，得

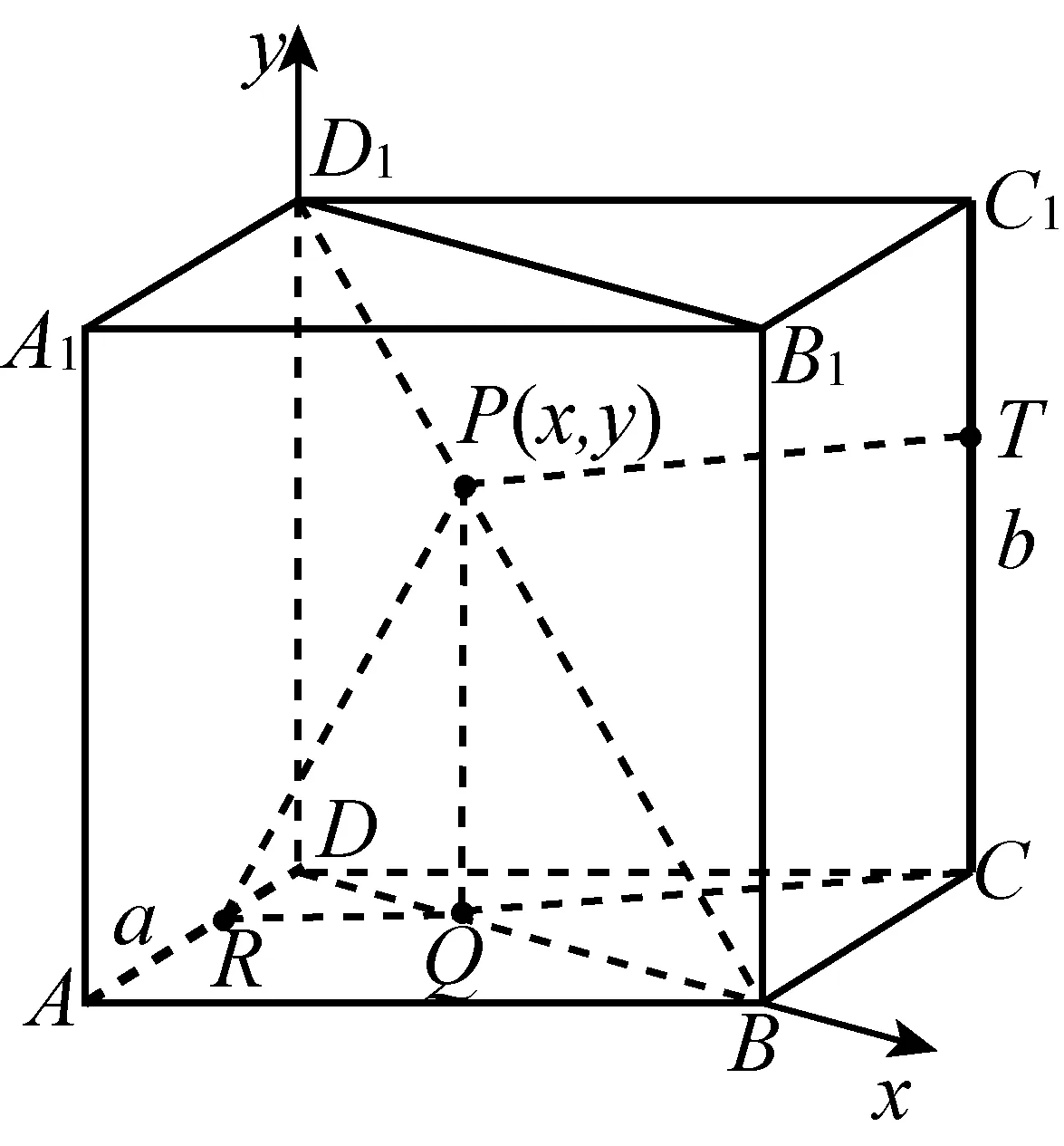
图14

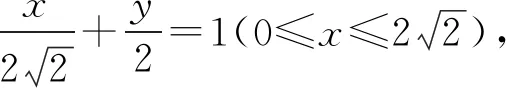
就是线段BD1. 答案：A

说明：如果是在平面DBB1D1内求轨迹，结果就是两条相交直线：

解法2(筛选法)该对角面上显然有共线的三点(点B、点D1和正方体的中心)在轨迹上，而选项B、C、D中的曲线上都不可能有三点共线. 故答案只能是A.

变式6如图15，在棱长为2的正方体ABCD-

A1B1C1D1的对角面ABC1D1内到异面直线a、b的距离相等的动点的轨迹是( ).

A.线段 B.圆弧

C.双曲线的一部分 D.抛物线的一部分

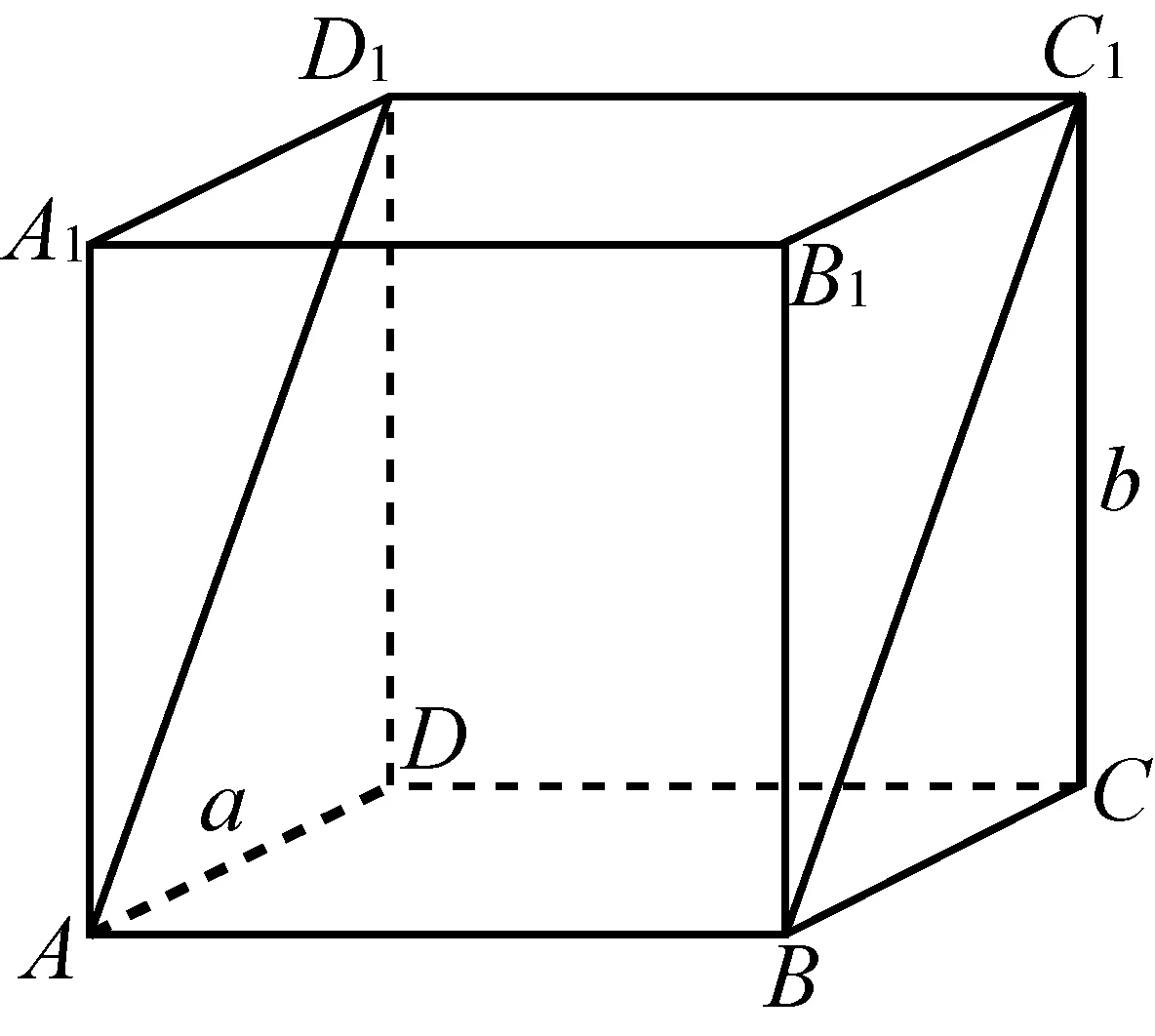
图15

解以AB为x轴，AD1为y轴，在平面ABC1D1内建立平面直角坐标系(图16).设点P(x,y)是对角面内任意一点，如图作辅助线，AQ=x,QP=y,由PS=PT，得

图16

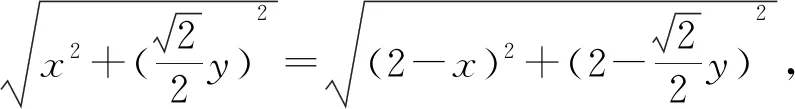
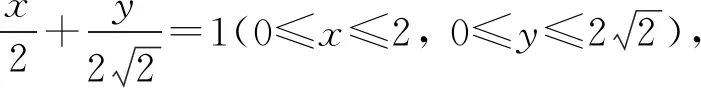
轨迹恰为矩形ABC1D1的对角线BD1(和变式5的答案方程不同，但却是同一条线段). 答案：A

变式7如图17，在棱长为2的正方体ABCD-

A1B1C1D1的对角面ACC1A1内到异面直线a、b的距离相等的动点的轨迹是( ).

A.线段 B.圆弧

C.双曲线的一部分 D.抛物线的一部分

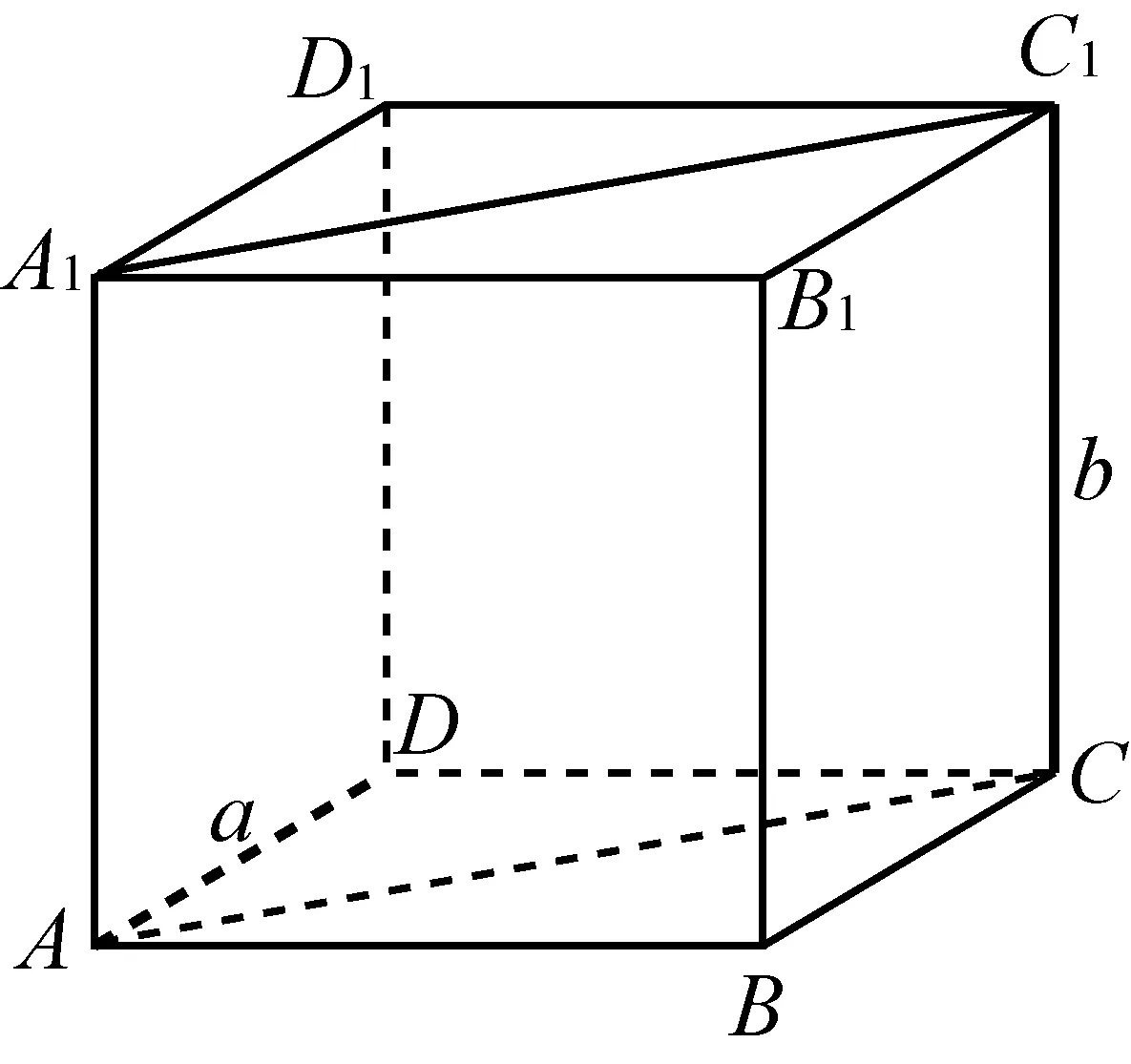
图17

分析：观察只能得出轨迹过对角面的中心，在对角面内不再过其它特殊点.难以直观判断.

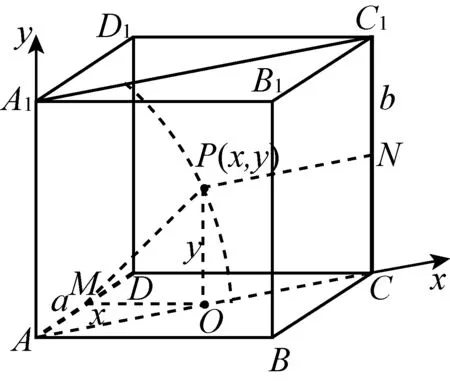
图18

化简得

轨迹是双曲线在对角面ACC1A1内的部分. 答案：C.

说明：此方程不是双曲线的标准方程. 故此题难度偏大，不宜作为高考练习题，可作为课外题或竞赛题.

变式8如图19，已知长方体ABCD-A1B1C1D1的长、宽、高分别是4、2、4，求正方形ABB1A1内到异面直线A1B和DC1(分别记为a,b)的距离相等的动点的轨迹方程，并画出轨迹.

图19

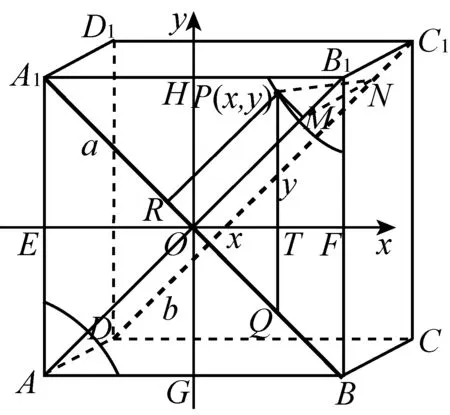
图20

解设正方形ABB1A1的四条边的中点分别是E，F，G，H(如图20), 以EF为x轴，GH为y轴，在平面ABB1A1内建立平面直角坐标系.设点P(x,y) (-2≤x≤2, -2≤y≤2)是正方形ABB1A1内任意一点，

如图作辅助线，x=OT,y=TP,QP=x+y,

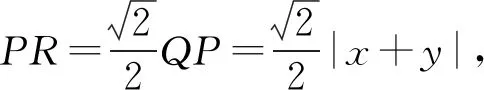
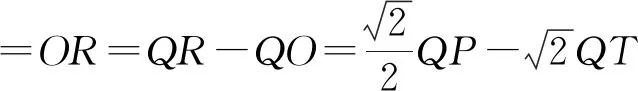
又MN=2，

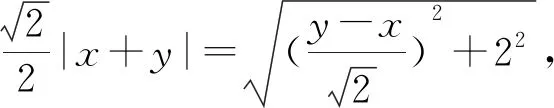
轨迹是反比例函数图像的一部分.

说明：(1)此题若分别以直线AB、AA1为x轴、y轴建立坐标系，则求出的方程是：

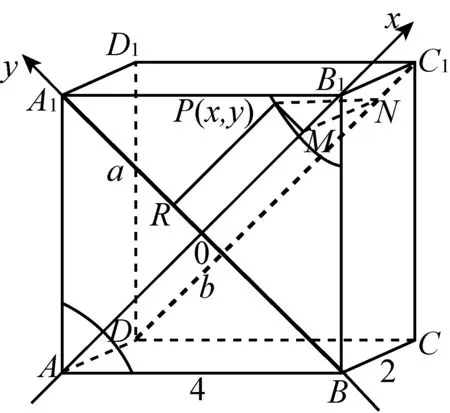
图21

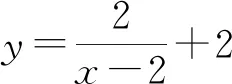
变式8把立体几何、解析几何、函数知识等都融会贯通在一起了，并且从一个独特的角度证明了反比例函数的图像就是解析几何中的等轴双曲线.是一个“含金量”很高的问题.

以上展示了由简单、特殊的轨迹问题出发，进行探索，进而发现所求轨迹是马鞍面，并研究了马鞍面的基本性质，再进一步发现轨迹(马鞍面)与正方体的六个面及其对角面所在平面的交线是抛物线、双曲线、相交直线或者一条直线这四种曲线之一，从而编出一系列轨迹问题的全过程.

以上八个变式通过解析法在立体图形中的运用，充分体现了对解析法的深刻理解和灵活运用, 从新的视角融合了立体几何与解析几何的知识和方法.

八个变式问题都是让学生解答在某个平面内的动点的轨迹问题，但实际上教师是在三维空间中研究问题，然后把结果投射到某个平面内来编题的，教师编题的视野和思维是比展现在学生面前的问题多了一个维度的！这样才能居高临下，编出新题、好题，才能有效培养和提升学生的数学思维品质和创新精神！