基于MPC含分布式光伏配电网有功功率—无功功率协调控制

张 颖, 季 宇, 唐云峰

(1. 中国农业大学信息与电气工程学院, 北京市 100083; 2. 中国电力科学研究院, 北京市 100192)

基于MPC含分布式光伏配电网有功功率—无功功率协调控制

张 颖1, 季 宇2, 唐云峰1

(1. 中国农业大学信息与电气工程学院, 北京市 100083; 2. 中国电力科学研究院, 北京市 100192)

为应对配电网中光伏出力和负荷需求的波动性和随机性,保证系统的安全与经济运行,提出一种基于模型预测控制的含分布式光伏配电网有功功率—无功功率协调控制方法。该方法将控制过程划分为长时间尺度优化控制和短时间尺度优化控制,不同时间尺度优化控制针对各自的控制目标及控制变量分别执行单独的模型预测控制。长时间尺度优化控制基于光伏出力及负荷需求预测信息,采用多步滚动优化求解有功、无功出力,短时间尺度优化控制以长时间尺度的优化控制结果为基准值,滚动求解有功、无功出力增量。长时间尺度及短时间尺度优化控制模型均为难以求解的非凸、非线性模型,本文将模型转化为二阶锥规划问题实现求解。采用改进的IEEE 33节点配电网系统进行算例分析,结果证明了所提优化控制方法的可行性和有效性。

模型预测控制; 有功功率—无功功率优化控制; 多时间尺度协调; 二阶锥规划

0 引言

近年来,随着分布式发电技术的不断发展,分布式光伏在配电网中的渗透率不断提高,对配电网的安全稳定运行提出了新的挑战[1-4]。

由于光伏出力及负荷需求具有随机性与波动性,预测误差随预测时间的提前而增大,增加了配电系统优化控制的难度,模型预测控制(model predictive control,MPC)能够克服系统的不确定性,是解决这一问题的有效途径,它在电力系统优化控制中的应用受到广泛重视[5-10]。文献[6-7]基于模型预测控制提出了含分布式电源电力系统的电压调节控制策略。文献[8]将模型预测控制用于大规模风电接入电力系统的有功调度控制中,对风电机组及传统机组进行优化控制,以提高系统运行的经济性。文献[9]将模型预测控制与大系统分层递阶控制结合,提出了将分层模型预测控制方法用于大规模风电接入电力系统的有功调度控制方法。文献[10]提出了基于模型预测控制的多时间尺度主动配电网多源协调优化调度策略,精细化协调控制和管理主动配电网中的分布式电源、储能以及柔性负荷。但上述文献多是对系统有功优化调度进行研究,并未考虑无功优化控制。

配电网线路的R/X比值较大,有功、无功功率的耦合性较强,二者对线路损耗、电压质量均有极大的影响,尤其是对于光伏渗透率较高的配电网,基于有功、无功解耦的优化控制方法已不适用,需考虑有功功率—无功功率协调优化控制。文献[11]建立了一种配电网有功功率—无功功率协调多时段优化模型,通过调节分布式电源、储能装置、电容器组实现优化控制。文献[12]提出了鲁棒区间电压控制方法,在计算出最优无功补偿决策的同时给出光伏电站的有功出力区间。文献[13]利用分布式电源及储能装置,建立了综合调度有功、无功优化控制模型,以提高分布式电源的并网水平、改善节点电压水平。但这些文献没有考虑光伏出力及负荷需求的随机性和波动性,而是将其作为确定量进行处理,而且通过智能逆变器接入配电网的分布式光伏具有一定的无功调节能力,在这些文献中也并未对此进行充分利用。

针对上述问题,本文基于模型预测控制,综合考虑配电网中多种可控装置,提出一种含分布式光伏配电网的有功功率—无功功率协调控制方法,将控制过程划分为长时间尺度优化控制及短时间尺度优化控制。不同时间尺度优化控制针对各自的控制目标及控制变量分别执行单独的模型预测控制。长时间尺度基于光伏出力及负荷需求预测信息,采用多步滚动优化求解各可控装置的有功、无功出力,短时间尺度以长时间尺度的计算结果为基准值,滚动求解有功、无功出力增量。通过采用模型预测控制方法及多时间尺度协调控制结构应对光伏出力及负荷需求的波动性和随机性,减小网络损耗,保证系统的安全与经济运行。

1 基于模型预测控制的优化控制策略

1.1 模型预测控制理论

模型预测控制是一种基于模型的有限时域闭环优化控制算法,具有易于建模、控制效果良好、鲁棒性强等优点,能够有效应对系统的非线性、时变性和不确定性,广泛应用于炼油、化工、冶金和电力等复杂工业过程控制中[14-15]。模型预测控制由预测模型、滚动优化和反馈校正三个环节构成。与传统的开环优化一次下发全部优化指令的优化方式不同,模型预测控制采用滚动优化策略,其机理为:在每一采样时刻,根据当前系统状态及测量信息,基于预测模型对未来状态的预测结果,在线求解一个有限时长的最优控制问题,得到当前时刻和未来时段内的控制行为,并只执行当前时刻的控制行为,在下一个采样时刻,根据前一时刻控制后的系统状态及新的测量信息,重复上述过程。

1.2 基于模型预测控制的优化控制策略

现有基于模型预测控制的优化控制方法多是对系统进行有功优化调度,这种调度模式为保证系统的安全运行要求,对系统内分布式能源有功出力进行了抑制[8-10],不符合分布式能源最大化利用的原则和发展方向。本文基于模型预测控制方法,综合考虑系统中的多种可控装置,提出一种基于模型预测控制的有功功率—无功功率协调优化控制策略。通过储能装置进行有功调节,通过有载调压变压器、补偿电容器组、静止无功补偿装置及分布式光伏进行无功调节,所提方法通过有功、无功功率的协调控制,最大化保证分布式光伏的就地消纳。并将控制过程划分为长时间尺度优化控制和短时间尺度优化控制,长时间尺度优化控制保证系统运行的经济性,短时间尺度优化控制保证系统运行的安全性,二者基于各自的优化目标分别执行单独的模型预测控制。长时间尺度优化控制以系统网损最小为优化目标,基于光伏出力及负荷需求的预测数据,以ΔT为时间间隔,对未来MΔT时间内系统中各可控装置的有功、无功出力进行优化求解,作为短时间尺度优化控制层的调节基点。短时间尺度优化控制根据当前系统运行状态及更小时间尺度的光伏出力及负荷需求预测数据,以Δt(Δt<ΔT)为时间间隔,滚动求解未来NΔt时间内系统中各可控装置的有功、无功出力增量,对上一级优化结果进行修正。基于模型预测控制的优化控制策略示意图如图1所示。

图1 基于模型预测控制的控制策略示意图Fig.1 Schematic diagram of MPC based control strategy

2 基于模型预测控制的优化控制模型

2.1 长时间尺度优化控制模型

长时间尺度优化控制以有载调压变压器及补偿电容器组挡位、静止无功补偿装置及分布式光伏无功出力、储能装置充放电功率为控制变量,以系统实际运行状态为初始值,以光伏出力及负荷需求的预测数据为输入变量,以ΔT为时间间隔,滚动求解未来MΔT时间内各可控装置的有功、无功出力。

2.1.1优化目标

为保证系统运行经济性,减少网络损耗,长时间尺度优化控制的优化目标为系统网损最小,即

(1)

2.1.2约束条件

1)潮流约束

针对放射网,本文采用Distflow形式表示潮流方程(式(2)至式(6)),其单条线路拓扑结构如图2所示。

(2)

(3)

(4)

(5)

(6)

图2 支路潮流模型Fig.2 Branch flow model

2)电压水平约束

(7)

3)支路容量约束

(8)

4)分布式光伏运行约束

(9)

(10)

(11)

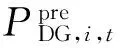
5)有载调压变压器运行约束

kij,t=k0+Kij,tΔkij

(12)

(13)

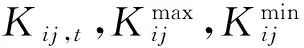
6)静止无功补偿装置运行约束

(14)

7)补偿电容器组运行约束

(15)

式中:Hi,t为可调挡位，Hi,t∈Z;ΔQc,i,t为调节步长;Hmax为补偿电容器组的最大可调挡位。

8)储能装置运行约束

(16)

(17)

(18)

2.2 短时间尺度优化控制模型

由于光伏出力和负荷需求的随机波动大,长时间尺度的预测数据误差较大,无法满足精度要求,因此增加短时间尺度优化控制,基于系统当前运行状态及更小时间尺度的预测数据对长时间尺度的优化控制结果进行调整,以Δt(Δt<ΔT)为时间间隔,滚动求解未来NΔt时间内系统中各可控装置的有功、无功出力增量。有载调压变压器和补偿电容器组响应速度较慢,且调整不宜过于频繁,因此在短时间尺度优化控制中不对二者进行调整,控制变量为储能装置充放电功率增量、静止无功补偿装置及分布式光伏无功出力增量。

2.2.1优化目标

由于光伏出力及负荷需求预测数据的误差随着预测时间的提前而增大,为应对二者的随机波动,防止出现电压越限,保证系统运行的安全性,同时为保证与长时间尺度整体优化方向及分析计算的一致性,短时间尺度优化控制仍以系统网损最小为优化目标。

(19)

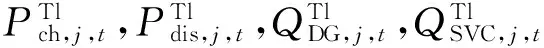
2.2.2约束条件

1)潮流约束

(20)

2)其他约束

(21)

式(21)包括电压水平约束、支路容量约束、分布式光伏运行约束、静止无功补偿装置运行约束及储能装置运行约束。

2.3 优化模型的二阶锥规划描述

本文所述优化问题中既包括连续变量又包括整数变量,其数学本质为混合整数非凸、非线性优化问题,难以求得最优解,本文考虑将优化模型转化为可高效求解的二阶锥规划(second-order cone programming,SOCP)问题。

2.3.1二阶锥规划

二阶锥规划的标准形式如下[16-17]:

(22)

式中:变量x∈RN;常量b∈RM,c∈RN,A∈RM×N;K为如式(23)和式(24)所示的二阶锥或旋转二阶锥。

二阶锥:

(23)

旋转二阶锥:

(24)

2.3.2优化问题的二阶锥规划描述

以长时间尺度优化控制为例,潮流约束中的式(3)与式(4)为非凸、非线性方程,优化目标函数及其他约束条件为线性方程,需对式(3)和式(4)进行处理。

式(3)与式(13)为对有载调压变压器的约束,采用基于分段线性化的精确线性化建模方法[18]对有载调压变压器建模,将该约束转化为线性约束。

对式(4)采用二阶锥方法[11]进行松弛,松弛之后,式(4)可改写为:

(25)

将其改写为标准二阶锥形式,即

(26)

长时间尺度优化控制模型中包含离散变量及连续变量,优化模型最终转化为混合整数二阶锥规划模型;短时间尺度优化控制模型中只包含连续变量,最终转换为二阶锥规划模型。

3 算例分析

3.1 仿真系统

本文采用改进IEEE 33节点系统进行仿真分析,系统结构如附录A图A1所示。在节点0,1间接入有载调压变压器,电压调节范围为[0.95,1.05](标幺值),8挡可调,调节步长为0.012 5(标幺值);节点30接入补偿电容器组,调节步长为50 kvar,调节范围为0～300 kvar;节点10接入静止无功补偿装置,无功补偿区间为0～500 kvar;节点17接入储能装置,容量为1 000 kW·h,充放电效率为95%,最大充放电功率为200 kW,其初始容量为500 kW·h;节点7,15,28分别接入容量为1 000 kW的分布式光伏。

本文仿真算例中长时间尺度优化控制以1 h为时间间隔,对未来4 h内系统内可控装置的有功、无功出力进行优化求解,作为短时间尺度优化控制层的调节基点。短时间尺度优化控制以15 min为时间间隔,滚动求解未来1 h内系统中各可控装置的有功、无功出力增量,对上一级预测结果进行修正。本文将优化模型转化为二阶锥规划模型,采用Mosek算法包求解。

3.2 仿真结果

光伏出力及负荷需求的预测曲线如附录A图A2所示,为验证本文所提控制方法应对光伏出力及负荷需求随机波动的有效性,在每一长期及短期滚动优化阶段分别添加一组-5%～5%的随机序列,模拟光伏出力及负荷需求的扰动量,作为模型预测控制的输入。

图3(a)给出了有载调压变压器和补偿电容器组的挡位调节情况,受其设备性能及响应时间的限制,只在长时间尺度优化控制中对其进行调整,可以看出二者的操作均出现在负荷与光伏大幅波动时。图3(b)给出了静止无功补偿装置的无功出力情况,为容性补偿,当光伏出力陡升至峰值时,由于分布式光伏的容量限制,分布式光伏的最大无功出力降低,故静止无功补偿装置无功出力大幅增加,当分布式光伏有功出力水平降低,分布式光伏可提供的无功出力增加,故静止无功补偿装置的无功出力有所减少。图3(c)给出了储能装置的充放电功率及荷电状态,储能装置的初始电量为500 kW·h,可以发现：当光伏出力接近于0时,储能装置发出电量；当光伏出力增加时,储能装置开始储存电量,负荷重载及光伏出力减少,储能装置释放电量,以实现系统安全稳定运行。图3(d)给出了分布式光伏无功出力的情况,其无功出力与其容量及接入位置有关,当系统处于光伏出力水平较低、负荷需求较高时,分布式光伏增发无功出力以满足系统安全稳定及经济运行要求。

优化前后系统根节点功率变化曲线如附录A图A3所示,由于本文所提优化控制方法不对分布式光伏的有功出力进行削减,只通过储能装置进行有功调节。从附录A图A3(a)中可以看出,放射网与主网的有功功率交换相差无几;从附录A图A3(b)中可以看出,本文方法可有效减少放射网从主网获取的无功功率,从而减少无功功率的长距离输送。

优化前后系统节点电压的对比图如附录A图A4所示,本文将节点电压约束设置为[0.95,1.05](标幺值)。选取两个典型场景：场景1为12:00时,光伏出力高而负荷需求相对较低,优化后系统网损明显降低,且节点电压均在安全范围内；场景2为20:00时,光伏出力低而负荷需求高,优化前节点电压越下限,优化后节点电压均在安全范围内。

图3 可控装置优化控制结果Fig.3 Optimal control results of controllable devices

优化前后系统网损的对比如图4所示。由图4可以看出,18:00后,由于光伏出力减小,负荷需求增加,故系统网损较其他时段较高,通过调节多种可控装置,其优化结果也较其他时段更好。通过对比发现,优化后系统的网损降低效果明显,这也证明了本文所提优化控制方法的有效性。

图4 优化控制前后系统网损Fig.4 Loss of system before and after optimal control

4 结语

本文针对光伏出力及负荷需求的不确定性和波动性问题,基于模型预测控制理论提出一种含分布式光伏配电网的有功功率—无功功率协调控制方法,该方法中不同时间尺度优化控制针对各自的控制目标及控制变量分别执行单独的模型预测控制,采用多步滚动优化求解系统中有载调压变压器、补偿电容器组、静止无功补偿装置、储能装置及分布式光伏的有功和无功出力,保证系统运行的安全性与经济性。同时,针对非线性优化的求解问题,采用二阶锥松弛方法进行求解,保证了算法的收敛性。通过算例分析,证明了该有功功率—无功功率协调控制方法的有效性。本文仅对含分布式光伏配电网的优化控制进行了研究,后续可针对含有多种分布式电源的有源配电网优化控制进行深入研究。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 丁明,王伟胜,王秀丽,等.大规模光伏发电对电力系统影响综述[J].中国电机工程学报,2014,34(1):1-14.

DING Ming, WANG Weisheng, WANG Xiuli, et al. A review on the effect of large-scale PV generation on power systems[J]. Proceedings of the CSEE, 2014, 34(1): 1-14.

[2] 王成山,李鹏.分布式发电、微网与智能配电网的发展与挑战[J].电力系统自动化,2010,34(2):10-23.

WANG Chengshan, LI Peng. Development and challenges of distributed generation, the micro-grid and smart distribution system[J]. Automation of Electric Power Systems, 2010, 34(2): 10-23.

[3] TAN Y T, KRISCHEN D S. Impact on the power system of a large penetration of photovoltaic generation[C]// IEEE Power Engineering Society General Meeting, June 24-28, 2007, Tampa, USA.

[4] 陈炜,艾欣,吴涛,等.光伏并网发电系统对电网的影响研究综述[J].电力自动化设备,2013,33(2):26-32.

CHEN Wei, AI Xin, WU Tao, et al. Influence of grid-connected photovoltaic system on power network[J]. Electric Power Automation Equipment, 2013, 33(2): 26-32.

[5] 刘向杰,孔小兵.电力工业复杂系统模型预测控制——现状与发展[J].中国电机工程学报,2013,33(5):79-85.

LIU Xiangjie, KONG Xiaobing. Present situation and prospect of model predictive control application in complex power industrial process[J]. Proceedings of the CSEE, 2013, 33(5): 79-85.

[6] 蔡宇,林今,宋永华,等.基于模型预测控制的主动配电网电压控制[J].电工技术学报,2015,30(23):42-49.

CAI Yu, LIN Jin, SONG Yonghua, et al. Voltage control strategy in active distribution network based on model predictive control[J]. Transactions of China Electrotechnical Society, 2015, 30(23): 42-49.

[7] 徐峰达,郭庆来,孙宏斌,等.基于模型预测控制理论的风电场自动电压控制[J].电力系统自动化,2015,39(7):59-67.DOI:10.7500/AEPS20140417004.

XU Fengda, GUO Qinglai, SUN Hongbin, et al. Automatic voltage control of wind farms based on model predictive control theory[J]. Automation of Electric Power Systems, 2015, 39(7): 59-67. DOI: 10.7500/AEPS20140417004.

[8] XIE Le, ILIC M D. Model predictive economic environmental dispatch of power systems with intermittent resource[C]// IEEE Power &Energy Society General Meeting, July 26-30, 2009, Canada.

[9] 张伯明,陈建华,吴文传.大规模风电接入电网的有功分层模型预测控制方法[J].电力系统自动化,2014,38(9):6-14.DOI:10.7500/AEPS20130712012.

ZHANG Boming, CHEN Jianhua, WU Wenchuan. A hierarchical model predictive control method of active power for accommodating large-scale wind power integration[J]. Automation of Electric Power Systems, 2014, 38(9): 6-14. DOI: 10.7500/AEPS20130712012.

[10] 董雷,陈卉,蒲天骄,等.基于模型预测控制的主动配电网多时间尺度动态优化调度[J].中国电机工程学报,2016,36(17):1-8.

DONG Lei, CHEN Hui, PU Tianjiao, et al. Multi-time scale dynamic optimal dispatch in active distribution network based on model predictive control[J]. Proceedings of the CSEE, 2016, 36(17): 1-8.

[11] 刘一兵,吴文传,张伯明,等.基于混合整数二阶锥规划的主动配电网有功-无功协调多时段优化运行[J].中国电机工程学报,2014,34(16):2575-2583.

LIU Yibing, WU Wenchuan, ZHANG Boming, et al. A mixed integer second-order cone programming based active and reactive power coordinated multi-period optimization for active distribution network[J]. Proceedings of the CSEE, 2014, 34(16): 2575-2583.

[12] 王永杰,吴文传,张伯明,等.有功无功协调的主动配电网鲁棒电压控制[J].电力系统自动化,2016,40(9):29-34.DOI:10.7500/AEPS20150613002.

WANG Yongjie, WU Wenchuan, ZHANG Boming, et al. Active and reactive power coordinated robust optimization for active distribution networks[J]. Automation of Electric Power Systems, 2016, 40(9): 29-34. DOI: 10.7500/AEPS20150613002.

[13] GABASH A, LI Pu. Active-reactive optimal power flow in distribution networks with embedded generation and battery storage[J]. IEEE Trans on Power Systems, 2012, 27(4): 2026-2035.

[14] 席裕庚.预测控制[M].北京:国防工业出版社,1993.

[15] QIN S J, BADGWELL T A. An overview of nonlinear model predictive control application[M]// Nonlinear Model Predictive Control. Birkhauser Basel, 2000: 3-32.

[16] ALIZADEH F, GOLDFARB D. Second-order cone programming[J]. Mathematical Programming, 2001, 95(1): 3-51.

[17] ANDERSEN E D, ROOS C, TERLAKY T. On implementing a primal-dual interior-point method for conic quadratic optimization[J]. Mathematical Programming, 2003, 95(2): 249-277.

[18] 刘斌,刘锋,梅生伟,等.基于二阶锥优化的含有载调压变压器主动配电网最优潮流[J].电力系统自动化,2015,39(19):40-47.DOI:10.7500/AEPS20150104003.

LIU Bin, LIU Feng, MEI Shengwei, et al. Optimal power flow in active distribution networks with on-load tap changer based on second-order cone programming[J]. Automation of Electric Power Systems, 2015, 39(19): 40-47. DOI: 10.7500/AEPS20150104003.

CoordinatedControlofActiveandReactivePowerforDistributionNetworkwithDistributedPhotovoltaicBasedonModelPredictiveControl

ZHANGYing1,JIYu2,TANGYunfeng1

(1. College of Information and Electrical Engineering, China Agricultural University, Beijing 100083, China; 2. China Electric Power Research Institute, Beijing 100192, China)

In order to solve the fluctuation and randomness of distributed photovoltaic (PV) output and load demand in distribution network and ensure the safety and economical operation of the system, a coordinated control method of active and reactive power for distribution network with distributed PV based on model predictive control is proposed. The method divides the control process into long-time scale optimization control and short-time scale optimization control. Based on the forecasting information on PV output and load demand, multi-step optimization is used to solve the active and reactive power output in long-time scale optimization control. Short-time scale optimization control uses the output of active and reactive power which is solved in the long-time scale optimization control as the reference value, and solves the active and reactive power output increment by multi-step optimization. The models are transformed into a second-order cone programming problem as both optimal models are non-convex and nonlinear, which are hard to solve. An improved IEEE 33-bus distribution network system is used to verify the feasibility and effectiveness of the proposed control method.

This work is supported by National Key Research and Development Program of China (No. 2016YFB0900400).

model predictive control; active-reactive power optimal control; multi-time scale coordination; second-order cone programming

2016-12-26;

2017-03-13。

上网日期: 2017-05-16。

国家重点研发计划资助项目(2016YFB0900400)。

张 颖(1994—),女,硕士研究生,主要研究方向:含分布式发电配电网优化控制。E-mail： zy0106@cau.edu.cn

季 宇(1982—),男,博士,主要研究方向:分布式发电、能源互联网运行控制技术。E-mail: jiyu@epri.sgcc.com.cn

唐云峰(1964—),男,通信作者,副研究员,主要研究方向:新能源发电。E-mail: tyf@cau.edu.cn

(编辑孔丽蓓)