基于等价观测方程的GPS/GLONASS组合多基线解算方法

储立新,陶 钧

(常州市武进规划与测绘院，江苏 常州 213159)



基于等价观测方程的GPS/GLONASS组合多基线解算方法

储立新,陶 钧

(常州市武进规划与测绘院，江苏 常州 213159)

进行独立参数化时，GNSS观测方程的双差、单差与非差观测方程理论上是等价的。利用按高度角定权的模型以及不同测站跟踪不同数量卫星的等价观测方程，实现基于简化等价观测方程的GPS/GLONASS组合多基线解算，包括多基线模糊度的固定、基线向量的解算与精度分析，并用多个测站的GPS/GLONASS同步实测载波相位和码伪距观测数据完成多基线解算分析。计算结果表明，由于多个测站的同时作用导致几何强度增强，降低模糊度间的相关性，有利于模糊度的快速解算；同时简化等价观测方程，提高法方程的形成速度，解算的基线精度也优于单基线解算模式。

等价性原理；GPS/GLONASS组合观测模型；模糊度；多基线解

全球导航卫星系统(GNSS)非差观测方程中含有一些无法用模型精确改正且又很难精确估计的冗余参数(如硬件延迟和初始相位)，这些参数大大增加计算负担[1-2]。采用差分技术在确保其他参数估值不变的前提下消除这些冗余参数，从而减轻计算负担。但在差分之后导致数学上的相关性，而这些相关问题通常很复杂，变换后的协方差阵不再是对角阵，在双差与三差模型中尤其复杂[3-4]。相对而言，GNSS非差模型有其自身的优势，如原始观测值都被充分的利用且权阵保留原始的对角阵；非差模型无须组建差分观测值，观测值之间不存在由差分引起的数学相关，有利于质量控制；非差模型较差分模型能更方便地对误差进行模型化；误差的绝对信息可以从估计量中获得，以便进行其物理特性和随机特征的研究，随着参考站增多，非差观测值较差分观测值更容易选择线性独立的基线[5-6]。

考虑到GNSS差分模型的缺点和非差模型的优点，一些学者一直关注于非差与差分模型间等价性原理的研究。Schafrin和Grafarend给出非差与差分模型间等价的理论依据，一旦权阵通过方差-协方差传播定律求出，所有方程在理论上都是等价的[7]。简化等价差分方程保留了非差与差分模型两者的优点，简化了数据处理模型。因此，本文实现基于等价观测方程的GPS/GLONASS组合多基线解算，大大提高数据处理效率。

1 GPS/GLONASS组合多基线网解模型

1.1 简化等价单差方程

GNSS非差观测方程可以表示为[8]

ε=Ax+By+Cz-l,P.

(1)

式中：y和z分别为与测站和卫星相关的参数，B和C是它们的系数阵且列满秩；x是用户关心的待估参数，A是它的系数阵且列满秩；l和ε分别是观测向量和正态分布的随机误差向量；P是权阵，考虑观测值按高度角加权，即P为对角阵。假设共有n颗卫星，k个测站，每个测站跟踪不完全相同的部分卫星，则

将所有的系数阵、观测向量和权阵按卫星顺序排列，则

(2)

按等价性原理[5,9]，消去卫星相关参数的变换矩阵，则

R=IΣk-CCTPC-1CTP=

(3)

消去卫星相关参数z的等价单差观测方程为

(4)

Pj,j=1,2,…,n.

(5)

其中，

(6)

1.2 简化等价双差方程

如果多个测站跟踪不完全相同的卫星时，简化等价双差观测方程的推导非常复杂。在不至于混淆的情况下，采用相同的符号将单差观测方程的系数阵、观测向量和权阵按测站重新分块组合，则

(7)

其中，

(8)

同样，消去参数y的变换矩阵

(9)

等价双差观测方程为

(10)

其中，

(11)

则等价的最小二乘解为

(12)

1.3 参数重整

这里以L1波段伪距和载波相位观测值为例，则非差观测值的线性化方程为

(13)

(14)

1.3.1 GPS非差观测方程的参数重整

1)在参数空间构造新的钟差组合，等式(13)右边加上再减去cδt1,P1，测站2的码伪距观测方程重新参数化为

(15)

式中:dt12,P1，dti,P1分别为伪距方程中接收机、卫星的等效钟差。在同一历元，dt12,P1作为新的接收机钟差对于每颗卫星是一致的，但不同频率不一样；dti,P1作为包含对流层和电离层延迟的新的卫星钟差对于两个接收机是一致的，但不同于每颗卫星上的各类观测值。

(16)

式中:在参数空间构成接收机等效钟差dt12,L1、卫星等效钟差dti,L1以及双差模糊度参数λ1。其中，只有随卫星变化而变化。因此，每颗卫星每一种类型的观测值对应一个dti钟差项。

3)因为Δr1=0，则测站1的伪距和相位观测方程可分别表示为

(17)

(18)

因此，单历元的GPS非差观测方程进行参数重整后可表示为

(19)

其中，n表示在该历元跟踪的卫星数，

dtL1=[dt1,L1dt2,L1…dtn,L1].

其余的非差观测值和卫星钟差仍然可以用上述方式简略表示。

从式(19)可以看出，非差GNSS定位函数模型经过参数重整后，不再存在设计矩阵秩亏，模糊度重整为双差形式；在单历元情况下，基于单频L1分析，观测n个卫星，原来模糊度参数为(测站数乘以卫星数)2n，现在的模糊度参数为n+1(接收机1的非差模糊度n个、接收机2相对于参考卫星的模糊度1个)。一般卫星数大于4颗，则经过参数重整后，模糊度参数明显减少。

1.3.2 GLONASS非差观测方程的参数重整

因为GLONASS每颗卫星的频率不同，因此对其模糊度项进行变形，则

(20)

这样，将原来的由两个单差模糊度组成的不具有整周特性的双差模糊度，变成一个具有整周特性的双差模糊度和一个与参考卫星的单差模糊度两部分。

同样，单历元的GLONASS非差观测方程进行参数重整后表示为(假设该时刻的参考卫星是26号卫星，s表示其他卫星)

(21)

2 GPS/GLONASS组合多基线网解数据处理与分析

2.1 数据来源

采集时间为2012-06-16(年积日为168)，采样间隔15 s，基线长度都在47～58 km左右。5个GNSS观测站中，SH01采用TRIMBLE NETR5接收机，SH02、SH03、SH04和SH05均采用TRIMBLE NETR9接收机。采集的GPS/GLONASS观测值类型有C1,P2,L1,L2观测值。

2.2 GPS网解和GPS/GLONASS组合多基线网解的基线精度比较

为了能够反映GPS网解与GPS/GLONASS组合网解收敛性与定位精度的差异，将5个原始观测文件均用TEQC软件切割为00:00～04:00时段，依次使用GPS和GPS/GLONASS组合观测值进行网解计算。

考虑到当前GLONASS观测值质量要略低于GPS，根据文献[6]用Helmert方差分量估计确定GPS/GLONASS的观测权，其相应的权比应该为1:0.25，文中也用该权比进行处理。另外，要得到站心坐标系下的NEU 3个分量，必须将结果从直角坐标系XYZ进行转换，其转换算式为

(22)

图1～图4给出该时段所有基线的解算结果，每个图从上至下依次代表与GAMIT的基线解算结果在N，E，U 3个分量上的偏差。

图1 基线SH01-SH02的定位偏差

图2 基线SH01-SH03的定位偏差

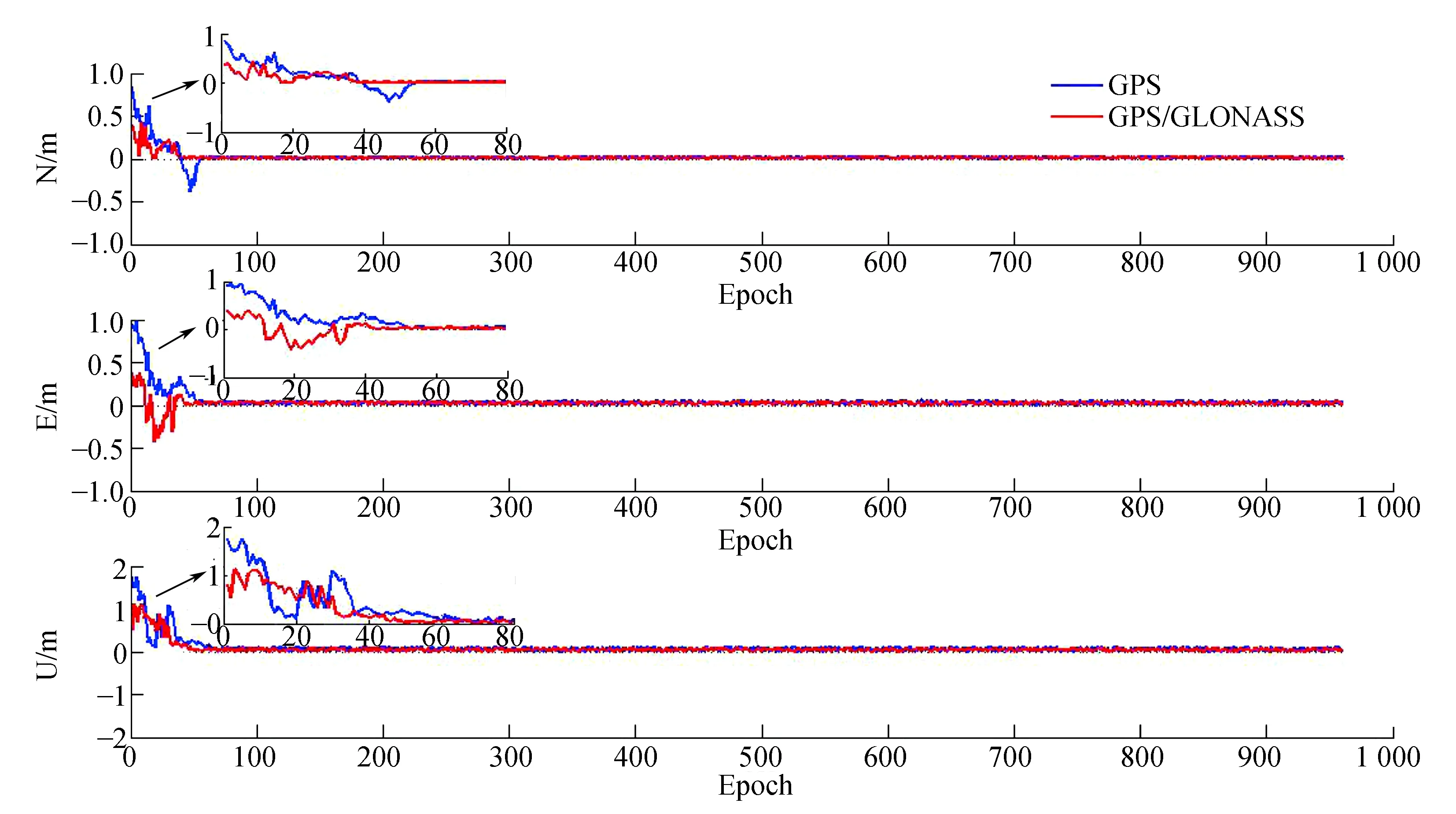
图3 基线SH01-SH04的定位偏差

图4 基线SH01-SH05的定位偏差

从图1～图4可以看出，从定位结果分析，各条基线在NEU 3个分量上均能在70个历元左右达到收敛，收敛后各分量的误差均接近于零。使用GPS/GLONASS组合多基线网解较使用GPS多基线网解的差异亦主要体现在收敛速度上，各基线各分量的收敛速度要稍快于GPS多基线网解的收敛速度。定位结果收敛后，两者的定位精度基本一致。以下是各条基线的分析结果：

1)基线SH01-SH02，从收敛速度来看，GG多基线网解在NEU 3个分量上均快于GPS多基线网解，在45个历元内基本都收敛；从精度上看，除在U分量上大致相当，在NE分量上，GG多基线网解均要优于GPS多基线网解。

2)基线SH01-SH03，从收敛速度来看，GG多基线网解在NEU 3个分量上均快于GPS多基线网解，在60个历元内基本都收敛；从精度上看，除在U分量上GG多基线网解均要优于GPS多基线网解，在NE分量上两者精度大致相当。

3)基线SH01-SH04，从收敛速度来看，GG多基线网解在NEU 3个分量上均快于GPS多基线网解，在75个历元内基本都收敛；从精度上看，在NEU 3个分量上，GG多基线网解均要优于GPS多基线网解。

4)基线SH01-SH05，从收敛速度来看，GG多基线网解在NEU 3个分量上均快于GPS多基线网解，在60个历元内基本都收敛；从精度上看，除在U分量上GG多基线网解均要优于GPS多基线网解，在NE分量上两者精度大致相当。

根据图1～图4各条基线的定位偏差结果，按式(23)计算各条基线收敛后的均方根误差RMS。

(23)

图5、表1分别为各条基线在收敛后的精度RMS统计图、统计表。

图5 各条基线收敛后的精度RMS统计图(m)

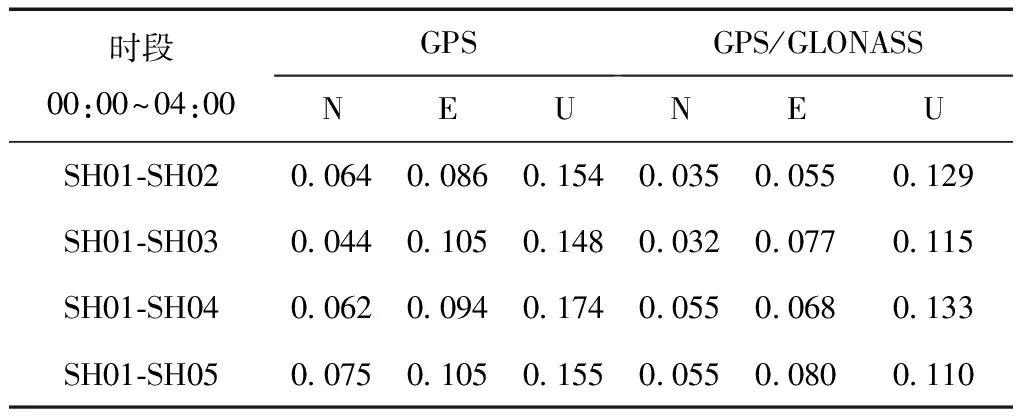
表1 各基线收敛后的精度RMS统计 m

由图5与表1可知，在时段00:00～04:00，基线SH01-SH02、SH01-SH03、SH01-SH04、SH01-SH05在采用GPS/GLONASS组合多基线网解后的精度较GPS单系统多基线网解在水平方向和高程方向均有改善，平面方向改进约1～3 cm，高程方向改进3～4.5 cm。其中，改进较大的基线SH01-SH02的N方向偏差由0.064 m降至0.035 m，E方向偏差由0.086 m降至0.055 m；而基线SH01-SH05 U方向改进最大，由0.155 m降至0.110 m；其他基线各方向的改进较小。

3 结束语

GPS单点定位[9]和GPS/GLONASS组合相位差分[10]的数据处理方法众多，本文根据等价性原理构建GPS/GLONASS 组合多基线网解模型，用该模型对上海观测网的数据进行处理，并与GPS单系统多基线网解的结果进行分析，得出以下几点结论：

1)从定位结果来看，与GPS/GLONASS组合多基线网解相比，使用GPS卫星进行多基线网解的收敛速度较慢，且定位精度相对较低，这主要是因为GPS单系统卫星数目较少，卫星几何图形强度不高造成的。

2)在未收敛阶段，GPS多基线网解的结果在NEU分量上的差值跳跃严重。引入GLONASS卫星后，卫星数目增加将近一倍，卫星几何图形强度得到显著改善，N，E，U 3个方向的收敛速度明显加快。

3)GPS/GLONASS组合多基线网解的结果对比GPS单系统多基线网解的结果在精度上有所改善，并在其稳定性和可靠性上较GPS均有所提高。

[1] LI B, SHEN Y. GNSS ambiguity resolution with constraints from normal equations[J].Journal of Surveying Engineering, 2009, doi: 10.1061/(ASCE) SU.1943-5428.0000017.

[2] 蔡昌盛,朱建军,戴吾蛟，等.GPS/GLONASS组合精密单点定位模型及结果分析[J].武汉大学学报(信息科学版),2011,36(12):1474-1477.

[3] 张小红,郭斐,李星星，等.GPS/GLONASS组合精密单点定位研究[J].武汉大学学报(信息科学版) ,2010,35(1):9-12.

[4] 马文忠,李林欢,江丽丽. 基于载波相位差分的北斗/GPS双模定位系统研究[J].测绘工程 ,2015,24(5):25-30.

[5] ODIJK D. Ionosphere-free phase combinations for modernized GPS[J]. Journal of Surveying Engineering.DOI: 10.1061/～ASCE，2003，0733-9453～2003,129:4-165.

[6] LIU Xianglin, JONG C D,TIBERIUS C C J M. Reparameterization of single difference and undifferenced kinematic GPS positioning models[M]. Geo-Spatial Information Science,2003(6):2,1-7,DOI: 10.1007/BF02826746.

[7] SCHAFRIN B,GRAFAREND E.Generating classes of equivalent linear models by nuisance parameter elimination. Applications to GPS observations. Manuscr Geodet,1986,11:262-271.

[8] 段举举,沈云中.GPS/GLONASS组合静态相位相对定位算法[J].测绘学报,2012,41(6):825-830.

[9] 高星伟,李毓麟,葛茂荣.GPS/GLONASS相位差分的数据处理方法[J].测绘科学,2004,29(2):22-24.

[10] 郑作亚,卢秀山.基于加权的伪距和历元间相位差分模型GPS单点定位方法[J].测绘科学,2007,32(5):47-49.

[责任编辑：张德福]

GPS/GLONASS integrated multi-baseline solutions by using the equivalent observation equations

CHU Lixin，TAO Jun

(Changzhou Wujin Planning and Surveying Institute, Changzhou 213159,China)

The double-difference, single-difference and zero-difference observation equations of GNSS are theoretically equivalent as long as the independent parameterisation. According to the fixed angle model and the equivalent observation equation of different station tracking numbers of satellites, this paper realizes the multi baseline solution of GPS/GLONASS combination based on the simplified equivalent observation equation, including multiple baseline ambiguity fixed, calculation of the baseline vector and the precision of the analysis. At the same time, the multi baseline solution analysis is also completed by using the GPS/GLONASS synchronous measured carrier phase and the code pseudo range observation data. The results show that the geometric intensity is enhanced due to the simultaneous action of several stations, and the correlation between the fuzzy degree is reduced to a certain extent, which is beneficial to the fast calculation of the degree of ambiguity; meanwhile the simplified equivalent observation equation can significantly improve the formation rate of the equation, and the baseline accuracy is better than that of the single baseline solution.

equivalent theory;GPS/GLONASS integrated observation model;ambiguity;multi-baseline solutions

2016-06-26

储立新(1971-),男,高级工程师.

10.19349/j.cnki.issn1006-7949.2017.03.001

P228

A

1006-7949(2017)03-0001-07

引用著录：储立新,陶钧.基于等价观测方程的GPS/GLONASS组合多基线解算方法[J].测绘工程，2017，26(3)：1-7.