助力学生发展 促进教师成长
——参加“说题比赛”的感悟与实践
金 鑫
助力学生发展 促进教师成长
——参加“说题比赛”的感悟与实践
金 鑫
江苏省南通中等专业学校 江苏南通 226000
通过参加南通市首届中学数学教师说题比赛,深刻体会到这种教研活动对于教育教学尤其是习题教学有一定的启示作用。“习题教学”是数学教学的重要组成部分,是数学学习的延伸与深化。通过以题为载体,“说”给同行听,“讲”给学生听的形式,来促进和优化习题教学,提高教师对习题和试题的拓展、变式和整合能力,进而提升课堂教学的实效性。
说题;讲题;评析;模拟课堂;习题教学
“习题教学”是中学数学教学的核心,是学生完善知识体系,培养应用能力的重要途径,是教师必备的教学能力之一。为促进中学数学教师进一步研究数学习题、试题,提高习题教学的能力,南通市教科研中心举行了首届说题比赛。笔者有幸参与其中,结合参赛经历,来谈谈笔者的一些想法和做法。
一、“说题”是什么
“说题比赛”是近几年涌现出来的一种新型的教学研讨形式,是备受各地青睐的选拔优秀教师,夯实青年教师基本功的一类做法。不同于以往的“说课”以课为载体,“说题”的对象转换为“题”,是课堂习题教学中的一个片断。各地举办的说题比赛,往往以书面的形式,从以下几个方面进行,即一阐述题意:说明题目的已知条件、难点的位置、估计难度、易错点等等,特别要说明题中的隐含条件;二题目背景:说明题目涉及的知识点及这些知识点在相应学段的数学地位,题目的来源、设计思路、命题意图、评价功能等等;三题目解答:给出这道题的正确解法,尽可能给出多种解法,要求保留解法中的重要过程(一些复杂的计算过程可省略);四总结提炼:说明题目涉及的数学思想方法,解题的基本规律;五题目变式:说出这道题可以进行怎样的变化引伸,并给出这些变式及其简要解答.所谓的“说题”大都是指上述这种“书面说题”的教研形式。
然而不同于其他的是,此次南通市教科研中心举办的说题比赛增加了“现场说题”这一环节。“现场说题”不是对“书面说题”的照本宣科,而是要求参赛教师以“模拟课堂”的形式将“书面说题”中的各部分内容串联起来,以课堂为载体展示出来。这就要求参赛教师在进行书面说题时除了关注以上所提的五个方面以外,还要关注到第六个方面教学设计:说明解题教学的基本策略、基本思路(思维链),解题的三个思维层次,展示启发引导的情景设计、问题设计,学法指导等等。“现场说题”将重点置于如何向学生讲授题目,因而称之为“讲题”更确切。
二、“讲题”与“说题”的关系
就区别层面而言,“说题”的对象一般是同行、专家,重点应放在题目的结构特征上,要侧重于对题目本身的研究,关注题目的来龙去脉,以剖析题目为目标。这是考验和提高教师解题能力,对题目的理解能力以及由此题延伸出去的拓展能力的重要途径和有效方法。“讲题”虽也以“题”为载体,但却以学生为传授对象,教学设计应以学生为主体,更多关注题目的教学价值和解法探究,以教会学生为目标.“讲题”更多地考验教师“习题教学”的能力,对学生思维方法的训练以及对解题方法技巧的提炼和反思。
就联系层面而言,“说题”关注的是“习题教学”方案的设计,“讲题”更关注“习题教学”方案的实施。如果说“讲题”呈现的是一部电影的话,那么“说题”则是这部电影的剧本。“讲题”与“说题”一脉相承,是“说题”基础上的课堂实施过程。
脱离了“讲题”,只搞“说题”,往往会“变味”成解题比赛,远离了课堂教学,违背活动初衷。融入“讲题”有利于凸现“说题比赛”对教学实际的指导作用;有利于构建教师主导学生主体的“习题教学”课堂;有利于改变教师原有的习题教学模式,促进教师探求新型的教学模式;只有如此,这个题才能“说”出实在,说出味道,说出功效。以下为笔者参赛中的书面说题稿及现场说题的教学设计(此设计获南通市区说题比赛一等奖)。
三、如何说题——书面说题稿
(一)原题重现
(二)说题流程
阐述题意→题目背景→题目解答→总结提炼→拓展延伸→教学设计
1、阐述题意
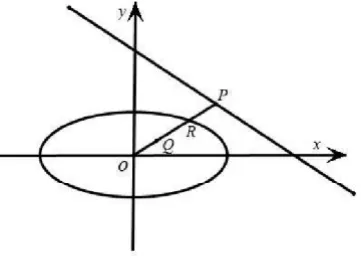
隐含条件:直线与椭圆的位置关系;OQ<OR。
待求结论:本题解答目标为“点Q的轨迹方程”,以及说明轨迹是什么曲线。
本题题眼:解答本题关键为利用“OQ OP=OR2”此条件解得Q点轨迹方程。
难度估计:①学生读题作图有一定的障碍;②从通法着手本题拥有的计算量较大;③在解答中会忽视对原点的考虑。综上:预估此题为中档的解析几何综合题。
2、背景出处
题源出处:本题为1995年全国高考理科卷第26题,涉及到苏教版必修二(第2章)“平面几何初步”和选修1-1(第2章)“圆锥曲线与方程”的相关知识。其中涉及的“直线的方程”在高考中为C级要求,“中心在坐标原点的椭圆的标准方程与几何性质”为B级要求。
设计意图:本题以能力立意,兼顾知识、方法的考查。
①知识要点:本题涉及直线和椭圆的方程、性质,直线与曲线的位置关系,曲线与方程的关系,轨迹的求解方法等基础知识;
②能力要求:本题关注学生的运算求解能力及推理论证能力,注重考查学生综合运用知识的能力;
③思想方法:本题注重对数形结合、函数与方程等解析几何基本思想的考查。
3、题目解答
解法1:由题意可知点Q不在原点。故设P、R、Q的坐标分别为 , ,其中x,y不同时为零。
当点P不在y轴上时,由O、R、Q三点共线可联立方程


再由OQ·OP=OR2可得

……………(※)
当点P不在y轴上时,亦满足上式。
解法2:由题意可知点Q不在原点。故设P、R、Q的坐标分别为 ,
当点P不在y轴上时,由O、R、Q三点共线可联立方程组

解得
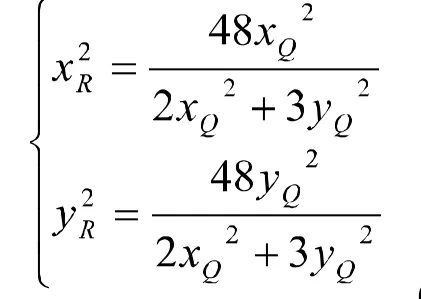
再由OQ OP=OR2得:代入(1)式解得

解法3:由题意可知点Q不在原点。故设P、R、Q的坐标分别为, , ,其中x,y不同时为零。
设OP与x轴正方向的夹角为 ,则由三角函数定义可知:xP=OP cos,yP=OP sin ;xR=OR cos ,yR=OR sin ;xQ=OQ cos ,yQ=OQ sin 。
由上式及题设OQ OP=OR2,得



4、总结提炼
数学思想方法:化归与转化、数形结合、方程的思想
解题基本规律:①对于求轨迹方程的一类问题一般步骤可归结为五字箴言:“建”、“设”、“现”、“代”、“化”。即:建系→设点→发现等量关系→代入→化简这五个基本步骤。
②直接法求轨迹方程的切口:“找等式入手”;关键:“依条件消参”。
5、拓展延伸
变式1:基于“结论一般化”原则拓展延伸
已知椭圆mx2+ny2=1 m,n>0 ,直线l:Ax+By=1(AB为 0),P是l上一点,射线OP交椭圆于点R,又点Q在OP上,且满足OQ OP=OR2.当点P在l上移动时,求证:点Q的轨迹方程为mx2+ny2=Ax=By。【证法同原题解法3】
变式2:基于“类比”原则将此题拓展延伸
(6)教学设计(略,见教学评析)
——作业改革探索与实践

