转化思想在小学数学课堂教学中的有效渗透

张香萍

转化思想在小学数学课堂教学中的有效渗透

张香萍

黑龙关中心学校 山西临汾 041200

数学新旧知识间有着千丝万缕的联系，而在这些知识点间发挥桥梁作用的正是数学思想。转化思想作为数学思想的核心，在小学数学教学中，紧扣“转化”这根弦展开实践探究，对学生各方面能力的提高有重要意义。

转化思想；小学数学；渗透

所谓转化思想，即一种化繁为简，化难为易的划归思想。该思想在小学数学课堂教学的有效应用，可实现抽象的、复杂数学知识向学生更易理解的、接受的数学知识转化。所以，我们在小学数学教学里，需结合具体教学内容，进行数学转化思想的渗透，有意识的依靠转化思想来增强学生的问题解决能力，提高数学学习效率。

一、结合实际，实现新旧知识的转化

小学生通过一段时间的学习，不管是从数学知识理解或从生活经验总结上均已有一定的储备，应用已学旧知识探究新知识也属于常用的数学教学模式。所以，小学数学教师在转化思想的渗透教学中，需基于学生知识掌握与学习能力的具体情况，于新旧知识点间架设一座转化的桥梁，实现二者的过渡，简化学习过程，促学生轻松掌握知识。

例如在教学“正方形周长的计算公式”相关知识点时，教师需牢抓长方形和正方形间关系，找出二者的相同点与不同点后，则注重转化思想的渗透，引导学生通过自主发现、思考与探究，得出正方形周长计算方法，且由此推导出相关计算公式。同时，在课前，教师可依靠现代信息技术为学生展示长方形的图片，引导学生回忆已学过的“周长的概念”和“长方形的周长计算公式”，当知识在学生大脑中回顾，并回答道：周长即图形的一周长度。长方形周长的计算公式为：（长+宽）×2后，教师则可为学生展示正方形图片，且提出问题：正方形的周长如何计算，周长计算公式是什么呢？鼓励学生联系旧知识，探索新知识，即可得出：正方形的周长=边长×4。这种新旧知识转化的教学模式，使学生获得新知识的同时，又达到了巩固旧知识的效果。

二、大胆联想，渗透转化思想

联想思维是发散思维的典型标志。联想思维的过程需由此及彼，从表到里。对学生展开联想思维的训练，可促学生思维达一定深度。在小学数学中，很多知识点都是可以通过联想来实现数学思想转化的，达到知识点的过渡，从而成功解决问题。

例如在教学《长方体和正方体的体积》时，教师就可先让学生结合计量长度方法进行经验总结：若要计量这条线段（见图1）的长度，你是怎样算的？再让学生结合计量面积的方法进行经验总结：若要计量这个长方形（见图2）有多大，你如何算？

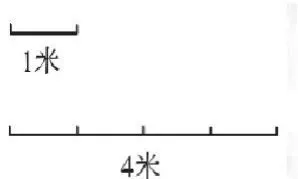
图1

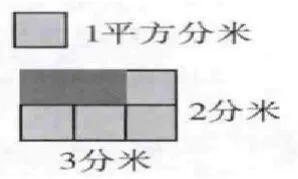
图2

学生通过观察与分析得到：计量线段多长，需看有多少个相同的长度单位；计量面积有多大，需看有多少个相同的面积单位。这实际上就是数学思想转化的过程，可达到知识点学习举一反三的效果。

随后，教师又可乘机提出问题：有一个大长方体，还有若干体积为1cm3的小正方体（见图3），怎样计量这个大长方体的体积？又可引导学生通过想象来达到数学知识的转化，那么学生就可由前面的计量方法，得出，使用单位体积小正方体填满大长方体，有多少单位体积的小正方体，则可得出大长方体的体积。

图3

这种通过联想的方式来实现问题的转化，更利于学生用最简单的方法解决问题，促学生发散思维得以培养，还能逐步推出长方体与正方体的体积计算公式。

三、解决问题，将转化思想内化为能力

转化思想在小学数学课堂教学中的渗透并非一朝一夕即可提高的，这需一个漫长的过程。转化思想应通过循序渐进的渗透与反复训练，方可真正让学生有所领悟，而解题则属于最有效的训练形式之一。数学习题解答与训练的过程实质是学生亲自感受与获取转化思想的过程，还是应用加深理解的过程。所以，教师在习题的选择上需从转化思想的渗透视角着手，设计一些满足学生学习水平的，实现新旧知识转化的习题，使学生对转化思想有程度不同的认识与理解。

例如，在学习了正方形的周长、圆的周长计算公式后，即可设计如下习题，要求学生计算下面图形的周长（见图4A、图4B），引导学生认识与应用转化思想。

图4 A

图4 B

由上图分析得出：这两个图形均属于不规则图形，如果直接计算较困难，若应用转化思想，可快速解题，即将图4A中的图形周长转化为边长等于1m的正方形，再用正方形的周长公式计算；把图4B中的图形周长转化为直径等于4cm的圆的周长和一个半径等于4cm的半圆的周长的和，再用圆的周长公式计算，整个知识点转化的过程，可提高解题效率与质量。

总之，转化思想在小学数学课堂的应用，在提高学生数学成绩，帮助学生轻松解题，促学生能力发展中有积极作用。教师需结合教材的编排体系，注重建构学生认知体系，认真钻研，读懂教材中蕴含的转化思想，引导学生实现思维的拓展。

[1]岳小芳.运用转化思想,让数学问题变得简单[J].课程教育研究，2017(32)：131.

[2]田静.应用“转化思想”加强小学数学教学[J].中国校外教育，2015(20)：141.