高安全性加密系统在智能电能表中的应用

张宏生

（国网安徽省电力公司计量中心，合肥230088）

0 引 言

随着国家智能电网的大规模建设，智能电能表等仪器设备得到广泛的使用和普及［1-3］。智能电能表作为国家电网用户终端的主要设备，它的安全性是至关重要的。如何提高电能表的工作安全性，如何提高总体的信息安全传输是一个亟需解决的重大难题。目前在一定程度上，自动化读取已经取代了传统的人工读取方式，但由于自动化读取作业不够成熟，加上信息的安全性不高，总体的系统运行效率还比较低。此外，由于智能电能表的具体运行环境中不确定因素较多，整个电能表的安全运行是越加复杂。

传统意义上的智能电能表只能进行用电数据的具体读取，但是对于读取数据的安全性传输或者处理则是能力十分有限。在具体的运行过程中，不可避兔的存在以下几个问题：（1）智能电能表被人为破坏，导致无法进行正常运行；（2）电能表读取的数据在中途传输过程中遭到破坏或者劫持，使得中央控制器收到不真实的信号；（3）智能电能表本身发生数据错乱。以上种种问题，都亟需一种新型安全系统嵌入电能表去解决。

针对以上所提问题的挑战，本文提出一种基于可编程逻辑器件（field programmable gate array：FPGA）［4］平台的高安全性椭圆加密系统［5］。该系统是从底层结构进行优化开始设计的：该系统设计首先从优化的有限域乘法器开始，再到中间的整体结构实现，最后到最终系统的实现完成。该系统采用硬件平台直接实现，因此在速度处理和运行效果上都取得较好结果。最后，该系统也被实际地应用在具体电网中得到检测验证。

1 智能电能表系统及安全系统

1.1 智能电能表系统

本系统可以针对单相智能电能表或者是三相智能电能表（这些电能表是在电能作业系统的基础之上建立的）。与传统的电能表系统相比，智能电能表的主要特点是所有的数据读取或者信号处理都是自动完成的。目前的智能电能表主要有直接型和间接型两种，对于作业环境要求复杂度高的地方就采用直接型的电能表系统。一般说来，一个智能电能表系统主要有如图1所示的系统组成。如图1所示，整个电能表系统的主要运行过程如下：

图1 智能电能系统组成图Fig.1 Structure diagram of smartmeter system

（1）计算测定输入：该工作单元执行整个电能表系统的第一步，主要是对智能电能表的数据输入进行计算处理（通常是进行模拟信号和数字信号的转换处理）。经过处理后的数据经过反馈进行再计算和在显示屏上进行显示；

（2）反馈：初步得出的数据有时会存在一定的误差（主要由运行环境所决定）。在这种情况下，电能表就需要对初步所得的数据进行反馈再计算以便随时调整整个电能表的计算系统；

（3）显示：该单元主要是对计算所得出的结果进行显示屏显示。一般是采用比较稳定的数字显示方式；

（4）检定输出：检定所得的结果会通过输送单元运输到控制中心。控制中心将所采集的数据进行集中协调管理。

1.2 椭圆曲线加密系统

椭圆曲线密码系统是近期应用比较广泛的新型公钥密码系统［5］。由于它具有复杂实现度低，安全性能高等特点，目前在各类信息处理系统得到广泛的应用。本文采用以椭圆曲线密码系统为基础的信息加密系统，它的主要原理如图2所示。

图2 椭圆曲线密码系统原理图Fig.2 Principle diagram of elliptic curve cryptographic system

如图2所示，在一个椭圆曲线密码系统中，A方和B方共同协议在一个系统中，由A方将信号传输到B方，同时B方将公钥释放给A方。两方之间进行如上的加密和解密的运算操作，使整个系统能够通畅进行。

具体到系统的实现层面上，加密系统的结构主要由一系列的基于有限域GF（2m）乘法器和加法器构成（当然包括其中的状态机运算）。在整个系统中，基于有限域GF（2m）乘法器占了很大比重。相比之下，基于有限域GF（2m）加法器的占用比率不是很大。因此，本文更加注重基于有限域GF（2m）乘法器的设计。本系统将通过底层突破的办法，层层递进，由下往上取得最终的结构。

2 椭圆曲线密码系统的优化设计

椭圆曲线密码系统可优化的地方主要集中在基于有限域GF（2m）乘法器的设计。本文通过对底层的基于有限域GF（2m）乘法器进行优化设计来取得整个加密系统的最优化实现。具体的设计过程如下：

2.1 基于有限域GF（2m）乘法器

美国国家标准局设定了基于有限域GF（2m）乘法器的次数，其中有m＝163 233 283 409 571。其中有两个是三项式，三个是五项式［5］。本文所设计的结构将建立在三项式上。

假定f（x）是一m次的不可约多项式在域GF（2）内，它的表达式可为：

其中 fi∈ GF（2） ＝｛0，1｝。那么集合｛1，x，…xm－1｝就是有限域GF（2m）的多项式的基。这样，在有限域GF（2m）内的一个多项式可表示为：

其中 ai∈ GF（2）。

假定 a（x），b（x）和 c（x）是在有限域 GF（2m）内的三个有限元。那么有限域的乘法可以由如下表示［6］：

其中：

bi∈GF（2），i＝0，1，…，m－1。同时 R（x）可以表示为：

其中gcd表示最大公除数。一般情况下，对于一个三项式f（x）＝xm＋xk＋1，R（x）＝xk是作为 Montgomery乘法因子。同时，R（x）有以下特性 R－1（x）＋f（x）.f′（x）＝1。那么整个乘法器的步骤就如下表示：

步骤1：H（x）＝a（x）b（x）.

步骤2：U（x）＝H（x）f′（x）mod R（x）.

步骤3：c（x）＝（H（x） ＋U（x）f（x））／R（x）mod f（x）。

对于三项式 f（x）＝xm＋xn＋1在域 GF（2）内。假定 T（x）＝t2m－2x2m－2＋… ＋t1x＋t0是 a（x）和 b（x）的乘积中间值，那么就有：

接着这个中间值T（x）也可以表示为：

接着再选择乘法因子R（x）＝xn，那么最终的乘法将有如下表示［6］：

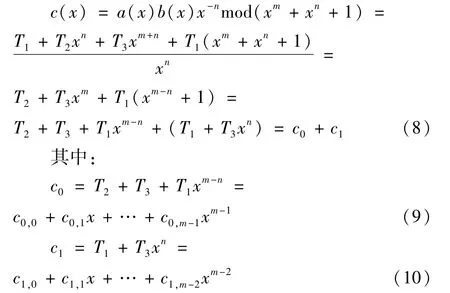
那么最终的乘法结果可以表示为：

2.2 有限域GF（2m）乘法器的硬件实现结构图

在这一部分里，关于乘法器的硬件结构图将具体地给出。本部分将具体展现结构来实现B1.A和B2.A。B1.A可以由信号流程图表示，如图3所示。它包括m个M节点和（m－1）个A节点。这些节点的功能在图3的小图中分别显示出来。

图3中，节点M是进行位乘运算，而节点A是进行位加法运算。本文同时又用了另外一个信号流程图来输入信号的转换过程，如图4所示，其中有m个S节点。这些S节点的功能主要是进行位移和转换，如图4（b）所示。根据式（9）中的运算，M1节点的输入应该是 b（x）：b0，b1，…，bm－1，而再进行位移运算转为次序如：bm－1，b0，…，bm－2。

根据图4的流程图进行时间上的切割和重新定义，可以得到初步的脉动结构如图5所示。在图5中，一个节点S，节点M和节点A被分在同一个区间里面。这样就使得设计完成后的脉动结构的关键路径为（TA＋TL＋TX），其中 TX，TL和 TA分别是 XOR门，寄存器和AND门的时间。

图3 乘法器的信号流程图Fig.3 Flow chart ofmultiplier signal

图4 乘法器的信号流程图Fig.4 Flow chart ofmultiplier signal

图5 输入信号流程图的关键路径切割Fig.5 Input signal flow chart of key route cutting

根据图4和图5所设计的最终结构图在图6所示，该结构由总共m个处理单元（Processing Element：PE）组成，每一个PE的内部功能在图6（b）有显示。设计完成后的结构需要在可编程逻辑器件上进行测试通过（图7是一具体的FPGA测试板）。FPGA器件具有处理速度快、效率高等特点，特别适合那些专门面向硬件平台开发实现的系统测试。整个测试的过程如下：

首先，对图6中的结构进行硬件描述语言的编程。程序设计完成后在某公司的编译软件ISE下进行编译通过和仿真测试验证。

接着，把程序下载到FPGA器件上进行实体仿真操作，同时得到具体的功耗、时间和占用面积等优化数值。如果数据不理想，需要重新返回第一步进行再仿真。

最后，通过测试的程序将连同FPGA器件安装到电能表系统中进行实际测试并观察具体运行效果。

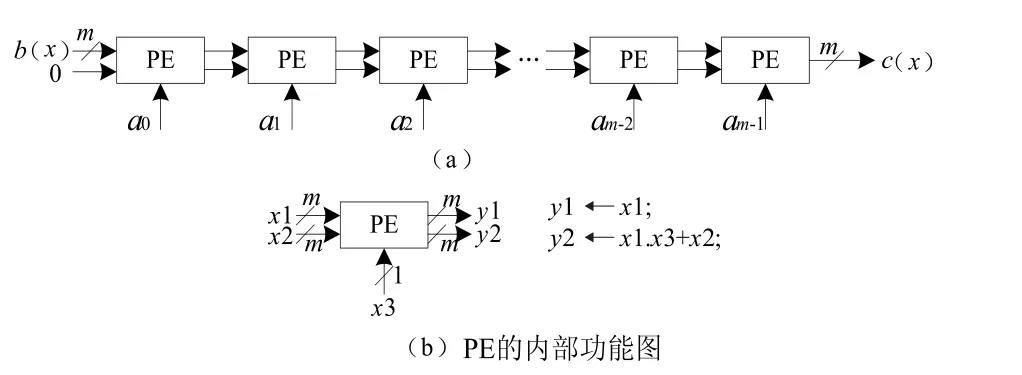
图6 最终结构图Fig.6 Final structure diagram

FPGA硬件电路板的结构图如图7所示。

图7 FPGA硬件电路板的结构图Fig.7 Structure diagram of FPGA hardware circuit board

3 加密系统的具体实现

在基于有限域GF（2m）乘法器的具体化硬件实现之后最终，该部分就被应用到整个椭圆曲线加密系统的结构里面。

3.1 椭圆曲线加密系统的具体实现

由于椭圆曲线加密算法主要是以基于有限域GF（2m）乘法器的一系列有规则的运算（当然也包括了基于有限域GF（2m）的加法器和平方器）。因此，本文采用有限状态机（finite state machine）作为主要的控制单元（然后也设计了基于有限域GF（2m）的加法器和平方器）。在基本的运算单元都实现了之后，就用控制单元对运算单元的进行调用控制从而实现最终的加密算法。当然，在状态机的运行过程中也需要对基本运算单元的结果进行临时存储以便在下一周期中使用（同时也需要一个选择器对基本的运算单元进行选择）。具体的最终结构如图8所示。

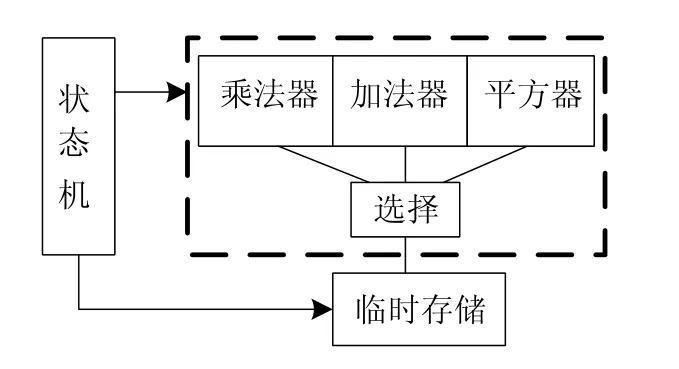
图8 加密系统结构图Fig.8 Structure diagram of cryptographic system

3.2 电能表系统的具体测试

加密系统的应用在基于FPGA（Xilinx Vitex-6芯片）平台的硬件测试中已经取得很好的优化效果（m＝233），如表1所示。无论是在面积、速度和功耗方面，都比之前的系统有所提高。

表1 加密系统的FPGA测试结果（m＝233）Tab.1 FPGA test result of cryptographic system（m＝233）

本文同时也将该加密系统具体应用到整个电能表系统中进行测试验证。以一自动化智能电能表系统为例，它的设计要求是每日的电能表检测量为7 600只，并且每日的数据检测量很大。

现设置具体的实验测试如下：

（1）数据准确性测试（无攻击状态下）

数据的准确性主要是指在安装本文所提出的加密系统后，中央控制器所接收到信号与电能表所发出的信号进行比较的概率。

在使用本文所提出的新型加密系统之后，单个电能表系统的运行量每日基本保持不变（但是数据传输的准确性大大提高，数据出错率减少到0.01%）。由于上述数据还是在单个电能表系统的运行下得出，当整个电网系统（由多条电能表线组成）都装上该加密设备后，那么所取得的综合效果就会非常突出，就如表2所示。

（2）数据准确性测试（有攻击状态下）

本步骤的测试采用最新型的SAT算法［7］对电能表所发出的每一个信息进行排查攻击（即进行排查猜测以猜出真实的原始值）。现有的智能电能表中所采用的简单数据加密主要采用了二进制混淆方法，即进行插入某一些逻辑算法（与门、或门等）以取得加密效果。

本步骤的测试对象是一组10只采用现有加密方法的智能电能表，另外一组是同样数量的采用了本文加密系统的电能表。在这两组电能表分别发出相同数据的情况下，一台高性能计算机（Intel处理器）采用SAT算法对这些信号进行攻击检测。所得出的具体结果（包括攻击所需要的时间）都显示在表3中。本测试时间限定在36小时。

表2 具体运行状况Tab.2 Concrete operation status

表3 攻击状态下的测试效果Tab.3 Test result under attacking conditions

由表3中可以看出，在使用本文所提出的加密系统后，在单个电能表系统和多个电能表系统，数据的安全性能大大提高。特别是现有的算法无法在短期内破解的优点决定了电能表在采用该类系统后的安全性能将大大提高。综合以上两方面的测试，可以看到该加密系统在电能表系统中的表现优异，值得在同类产品中大力推广。

4 结束语

本文通过对智能电能表中嵌入加密系统的具体分析和讨论，结合椭圆曲线加密优化算法的硬件实现的具体优势，对现有的智能电能表信号处理的自动化作业进行优化处理。多方面的结果证明本文所提出的方法在电能表的具体运行中有优异表现，在保证不影响具体作用的同时，取得信息安全方面很大幅度的提高。由于该加密系统在电能表中的应用设计合理、效率极高，值得在国家电网建设中大力推广使用。