基于多种群遗传算法的波浪发电最大功率跟踪控制*

邹子君，杨俊华，杨金明

（1.广东工业大学自动化学院，广州510006；2.华南理工大学电力学院，广州510641）

0 引 言

波浪发电是一种新能源发电形式，波浪能功率密度大、可预测性好，发展潜力良好。如何实现波浪能的最大功率点跟踪，是波浪发电研究的关键技术，目前，有三种常见的控制（MPPT）策略：锁存控制、模型预测控制和共轭控制。文献［1］提出的波浪发电锁存控制策略，可实现MPPT控制，但控制效果与浮子最佳释放时间点的准确估计直接相关。文献［2］将模型预测控制应用到点吸收器控制中，适用于可用线性模型描述的任意点吸收器，且在目标函数中考虑能量转换损失，可获得更好的实际控制效果，通用性强。但该方案过度依赖于数学模型，建模误差直接影响实际控制效果；控制器设计过程，需提供足够精确的波浪力在线预测值，实现困难。文献［3］采用共轭控制策略，通过调节发电机阻抗，使之等于波浪发电装置阻抗的共扼值，从而满足Falnes提出的相位条件［2］，最大限度地捕获波浪能。文献［4］提出了反应式控制策略，仿真结果表明，该策略可明显提高长周期不规则波浪条件下的波浪能捕获功率值。但控制效果的有效性与波浪发电装置吸收波浪力的大小有关，实际海况中波浪能捕获装置吸收的波浪力，不足以体现其控制效果。文献［5］在阿基米德摆式装置（AWS）中采用反馈线性化控制策略，有效减少了非线性饱和、死区对系统控制效果的影响，仿真结果也表明该策略能增加装置吸收的波浪能，然而实际系统中的非线性因素影响无法完全避兔，实际控制效果不理想。文献［6］将内模控制应用于波浪发电系统，可提高102%的波浪能捕获值，但控制的有效性依赖于系统中模型估计的精确度。文献［7］在AWS的内模控制器中引入神经网络模型，不同于以往的线性模型，该模型利用大量实验数据训练神经网络，与实际系统误差更小，改善了控制效果。但控制效果有较明显的季节性，夏季效果不理想。为克服内模控制器的缺点并吸收较多的波浪能，文献［8］提出内模切换控制，通过不同的隐含层神经元数目和训练次数，得到夏季和冬季两个AWS神经网络模型，通过切换内模控制器中的季节模型，实现控制效果的全年优化，但切换动作会影响系统稳定性。

MPPT实质上是一个优化问题，目标是使波浪能捕获率的值最大，接近理论最优值1。遗传算法是一种有效的目标优化工具，已较多应用于光伏电池阵列及风力发电系统中［9-12］。但传统遗传算法，仅有单一种群的遗传操作，在适应度函数值较大个体的影响下，易使种群中的个体较快趋于单一化，群体更新较快停止且易出现未成熟收敛，导致波浪能捕获率的最终结果并非最优解。为此，本文将多种群遗传优化算法与波浪发电的MPPT结合，在初始阶段，算法引入多个种群同时进行搜索，并对每个种群赋予不同的交叉、变异概率，使算法能够兼顾全局与局部搜索；同时加入用于维持种群间联系的移民算子及可用来建立精华种群的人工选择算子，并以精华种群作为算法收敛的判据，使各种群产生的最优个体通过精华种群实现留优。仿真结果验证了算法的有效性及实用性。

1 波浪发电系统的数学模型

振荡浮子式波浪发电系统，一般由浮子、质量块和弹簧、直线发电机等构成。浮子是主要的波浪能捕获机构，其捕获波浪能的能力与所受波浪力的大小直接相关，圆柱形浮子受力最大［13］。为实现最大波浪能捕获，毫无例外均采用圆柱形浮子进行分析。若浮子采用柱体形状，则浮子在水中的静浮力与其位移成正比，设浮子在平静水面所处的位置为平衡位置，可得［14］：

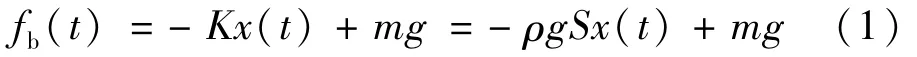
式中fb（t）是水中时的浮子静浮力；ρ为水的密度；g为重力加速度；S为浮子有效横截面积；m是波浪发电系统的总质量；x是竖直方向上系统偏离平衡位置的位移；t是时间。

浮子随波浪振荡时会产生辐射波，幅射波与海水相互作用会产生辐射力，根据波浪理论［14］，辐射力可表示为：

式中fr（t）是辐射力；ma和Ra分别表示因辐射力产生的附加质量和附加阻尼。

通过由弹簧和质量块构成的振动结构，浮子捕获的波浪能驱动直线发电机的动子切割磁场产生电势，将波浪能转化为电能。直线电机的电磁力可表示为速度和位移的线性组合［15］：

式中fg（t）表示直线电机的电磁力；Rg为反映直线电机吸收有功功率能力的阻尼系数；Kg为反映直线电机吸收无功功率能力的弹性系数。

根据牛顿第二定律，可获得波浪发电系统运动方程：

式中fe（t）是海浪激励力，表示入射波作用于浮子上的力；fv（t）和 ff（t）是粘滞力和摩擦力，通常可忽略不计，于是可将式（1）～式（3）代入式（4），得到振荡浮子式波浪发电系统的动力学方程：

2 系统输出功率分析

忽略电机电磁损耗，系统输出的瞬时功率为［14］：

波浪发电系统输出功率瞬时值的时变性很大，要了解系统从波浪中吸收能量的实际情况，需要分析系统输出功率的平均值，频域分析更加有效方便。为此，对式（5）进行傅里叶变换，得：

将s＝jω代入上式，有：

波浪发电系统复功率的实部即为平均功率：

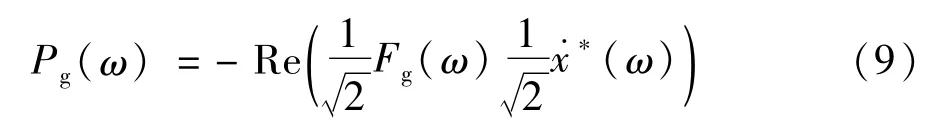
对式（9）进行化简，可得波浪发电系统的平均功率为：

由上式可以看出，理论上波浪发电系统平均功率的最大值为：

式（10）中，附加阻尼Ra是海浪频率的非线性函数，波浪力Fe可用余弦函数表示，其频率等于波浪运动频率［14］，一定频率下 Ra和 Fe的数值是固定的。因此为实现波浪能的最大捕获，使波浪发电系统输出的平均功率尽可能接近于最大值，可利用多种群遗传算法的寻优能力，通过不同频率下的迭代计算，迅速找到最大功率点对应的二维变量组［Rg，Kg］，使波浪能捕获率η，即：

有最大值，实现不同频率下系统输出功率最大化。

3 多种群遗传算法

遗传算法是一种仿效生物界“适者生存”法则的随机全局概率搜索算法，但存在未成熟收敛现象。多种群遗传算法，通过引入多个种群同时进行优化搜索，并对每个种群赋予不同的交叉、变异概率取值，兼顾实现算法全局搜索和局部搜索，同时引入实现多种群协同进化的移民算子及作为算法终止判据的精华种群。如此，可较好解决传统遗传算法的早熟收敛问题，多种群遗传算法的流程图如图1所示。

多种群遗传算法的计算步骤如下：

（1）生成初始群体：设定子种群个数为10，每个子种群中有40个个体，随机初始化种群；

（2）适应度评估：计算子种群中每个个体的适应度函数值；

图1 多种群遗传算法的流程图Fig.1 Flow chart of themultiple population genetic algorithm

（3）选择、交叉、变异：从各个子种群中根据个体的适应度函数值选择个体，然后各个子种群根据不同的交叉、变异概率完成个体的交叉、变异操作。各子种群的交叉概率Pc和变异概率Pm的取值分别为：

式中MP为子种群数目，本算例中取为10；

（4）移民、人工选择精华种群：将目标种群最劣个体用源种群的最优个体替换，实现种群间优秀个体的基因交流，然后找出移民后各子种群的最优个体，将最优个体的编码及其适应度函数值放入精华种群加以保存；

（5）收敛条件判断：比较精华种群中当前的最优值与前一次进化所得最优值的大小，若当前的最优值较大，则更新最优值，与最优值保持代数；若当前的最优值较小，则在最优值保持代数上加1，并判断最优值保持代数是否大于10，若是，则算法结束，返回最优解，否则返回步骤2。

4 仿真结果及分析

为验证多种群遗传算法的有效性，建立了小型波浪发电系统的MATLAB／Simulink仿真模型，主要参数为：动子质量 m＝45 kg，附加质量ma＝0 kg，辐射力阻尼系数 Ra＝300 N.S／m，浮子系数 K＝800 N.S／m。

图2～图4分别给出了波浪周期T为1 s，2 s，3s时，运行5次遗传算法和多种群遗传算法的波浪能捕获率进化过程图，以图2为例进行说明。图2（a）和图2（b）中均有5条波浪能捕获率曲线，表示算法运行5次的进化过程，图2（a）采用遗传算法，图2（b）采用多种群遗传算法。由图可知，图2（b）中曲线进化到第7代，均已稳定下来，而图2（a）中的曲线，需进化到第27代，始才逐渐稳定。也就是说，在成功寻优的迭代次数上，多种群遗传算法寻优速度更快，远少于遗传算法。多种群遗传算法中，各子种群通过移民算子进行个体优秀基因交流，大大提高计算寻优效率。

表1～表3分别为波浪周期T为1 s，2 s，3 s时，两类算法每次运行得到的波浪能捕获率最大值及对应的二维变量组［Rg，Kg］，以表1为例进行说明。由表1可知，遗传算法5次得到的优化结果均不相同，说明最优解仍有上升可能，算法稳定性不好；且算法多次陷入局部最优，存在早熟收敛的情况。表1显示，多种群遗传算法运行5次的结果完全一致，算法稳定性较好，且波浪能捕获率可达到理论最大值1，降低了波浪能损失。

图2 周期为1 s的波浪能捕获率曲线图Fig.2 Curves of the capture rate of wave energy having T＝1s

图3 周期为2 s的波浪能捕获率曲线图Fig.3 Curves of the capture rate of wave energy having T＝2 s

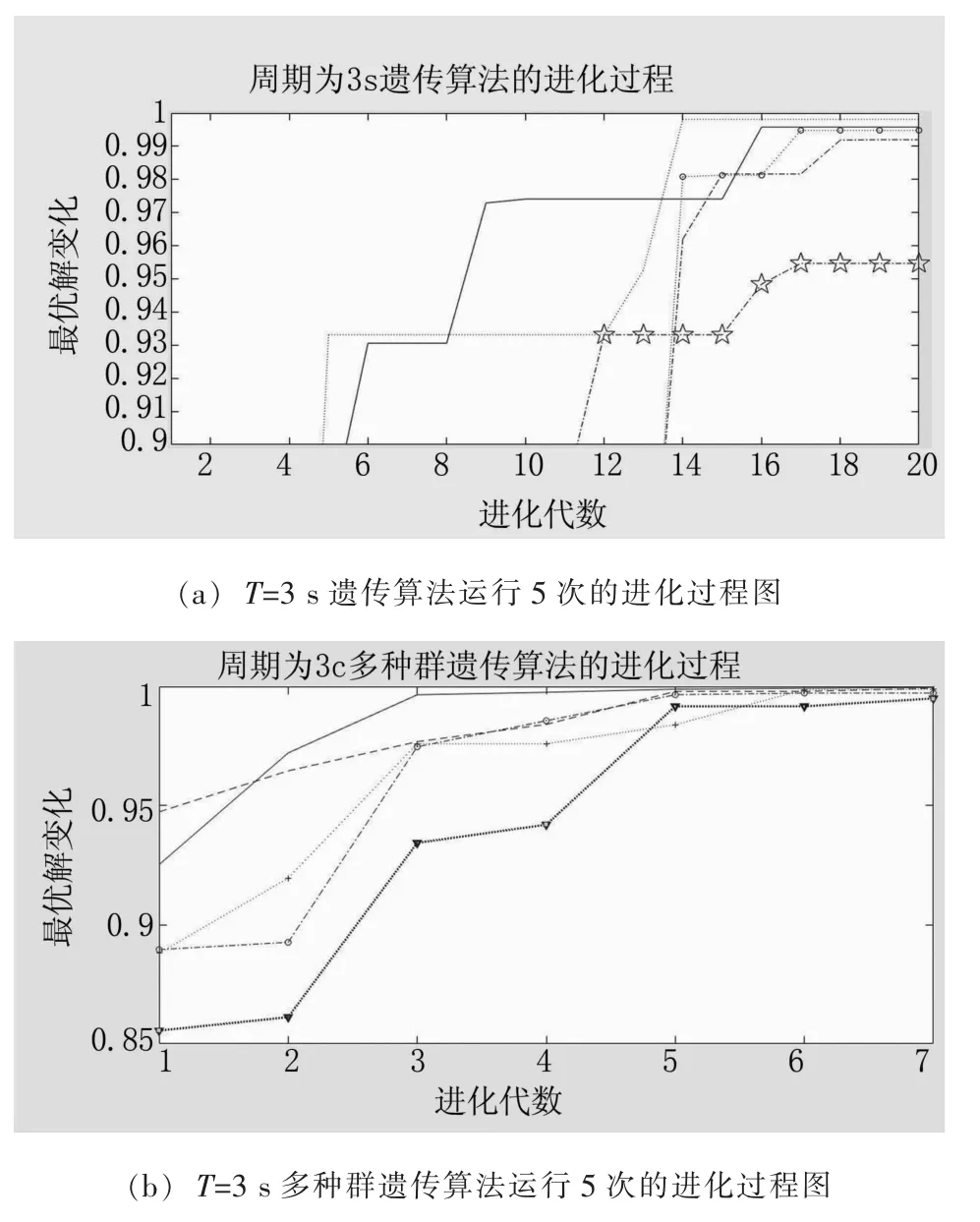
图4 周期为3 s的波浪能捕获率曲线图Fig.4 Curves of the capture rate ofwave energy having T＝3 s

表1 周期为1 s的波浪能捕获率最大值及对应的R g、K gTab.1 Maximum of the capture rate of wave energy having T＝1 s and the corresponding R g，K g

表2 周期为2 s的波浪能捕获率最大值及对应的R g、K gTab.2 Maximum of the capture rate of wave energy having T＝2 s and the corresponding R g，K g

表3 周期为3 s的波浪能捕获率最大值及对应的R g、K gTab.3 Maximum of the capture rate of wave energy having T＝3 s and the corresponding R g、K g

5 结束语

多种群遗传算法应用于波浪发电最大波浪能捕获，可在解空间中采用多个种群，同时进行协同搜索，并通过对各个子种群设置不同的变异和交叉概率，兼顾全局搜索和局部搜索。同时，优秀个体在种群间实现流动，有利于传播优秀基因。以精华种群的最优个体最少保持代数作为算法结束的终止条件，提高了算法收敛的合理性。仿真结果表明，与遗传算法相比，该算法在寻优速度、算法稳定性方面有较大改进，并能有效抑制GA的未成熟收敛现象，提高波浪能捕获率，可用于实现波浪发电系统的最大功率点跟踪控制。