基于粒子滤波与EEMD的低频振荡模式识别方法研究*

曾林俊，肖辉，江维，邓仕燊，杨俊琛

（1.长沙理工大学，长沙410114；2.国网株洲供电公司，湖南 株洲412000；3.国网福建龙海市供电公司，福建 龙海363100）

0 引 言

随着我国电力工业的不断发展，电力系统规模不断扩大，已经扩展成了大区域互联电网。此种情况有利于改善输配电的运行经济性和可靠性，但区域电网互联有可能引发低频振荡现象［1］。在采用励磁控制器的条件下，低频振荡发生的几率不断提高，如果无法很好的对低频振荡进行抑制，电力系统的稳定性将遭到破坏。而对低频振荡的模式识别［2－3］，有助于了解系统的动态性能，为安全预警提供较好的分析结果。

现有的低频振荡模式分析方法，基于数值解的分析法如传递函数法，及基于实测信号的分析法，如ESPRIT、FFT、小波分析等大部分对线性系统有良好的辨识效果，传递函数法通过对系统输入信号，再由反馈信号寻找到系统内部的某种对应关系，进而可判断系统的稳定状况等，但当系统非线性程度较强时，传递函数法［4］所计算的变量关系将会十分复杂；ESPRIT算法［5-6］假定振荡信号可表示为一系列指数函数的线性组合，未一起使用复观测数据及其共轭数据进行参数估计，且在低信噪比下的性能较低，使得辨识精度不高，同时对非线性信号的分析有一定的限制；FFT［7-8］在分析含噪的非线性、非平稳信号上显得不够理想，无时域分析功能，无法自适应反映信号的时变特性，且频率分辨率不高，难以满足非平稳信号分析的需要；小波分析法［9］可用于非线性系统，但小波基难以选择且存在频率分辨问题。现有的分析方法对于非线性非高斯的复杂系统的去噪和参数估计方面处理效果不是很理想，有一定的误差，然而电力系统大部分都是含噪的非高斯非线性复杂系统，现有方法无法很好地满足非高斯非线性复杂系统的需要。

为克服现有方法的不足，本文提出一种识别低频振荡模式的新方法，即将前置粒子滤波去噪算法与时频分析法-EEMD［10-12］相结合，利用粒子滤波对非高斯非线性系统处理的优势，对振荡信号进行去噪，再对去噪后的信号使用EEMD进行模态分解，检测出低频振荡模式。最后，通过算例仿真，验证了本方法的正确性和可靠性。

1 粒子滤波算法

1.1 粒子滤波理论

粒子滤波［13-16］（Particle Filter，PF），又称为序贵蒙特卡罗（Sequential Monte Carlo，SMC）方法，是一种基于SMC方法的贝叶斯滤波技术。其基本原理是寻找一组在状态空间传播的随机粒子（样本）描述系统的状态，通过SMC法简化贝叶斯估计中的积分运算，进而得出系统状态的最小均方差估计。在粒子数接近无穷时能逼近服从任意概率分布的系统状态。相对其它滤波技术而言，粒子滤波［17］不需要对系统状态作任何先验性假设，原理上能用于可用于状态空间模型描述的任何系统。

系统的状态空间方程包含状态方程和观测方程，其模型描述如下：

状态方程：

观测方程：

式中xk∈Rnx是系统的状态值；yk∈Rny是观测值，f（·）、h（·）表示状态方程和观测方程；uk为过程噪声；vk为观测噪声，其都服从高斯分布。模型中假设状态转移过程服从一阶马尔科夫模型，即时刻k的状态xk只和前一时刻k－1的状态xk－1有关，且模型中观测值间相互独立，即观测值yk只与k时刻的状态量xk有关。根据贝叶斯估计原理，在已知观测量 y1：k的前提下，x1：k的后验概率分布为：

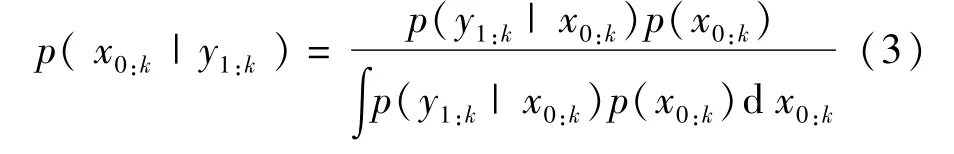
其中，p（x0：k）表示先验概率密度；p（y1：k｜x0：k）表示观测量，为y1：k时的似然概率密度。

将上式（3）与Monte Carlo原理相结合，从后验概率密度 p（x0：k｜y1：k）中抽取 N个相互独立的样本来求解函数估计值，如期望或方差。但是在实际很难直接通过后验概率密度函数取样，一般引入重要性密度函数 q（x0：k｜y1：k）和其相应的权值，权值计算式为：

为进一步解决计算量较大的问题，将权值按照下式进行归一化处理：

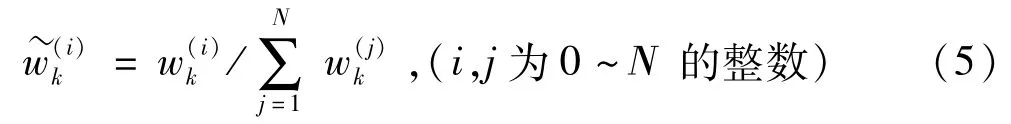
从而根据以上各式，后验概率密度可以近似的表示为：

其中，δ（）·表示狄拉克delta函数。

1.2 重要性函数及重采样

PF算法存在的主要不足为粒子数匮乏，样本权值退化，粒子数多样性缺失。现在对PF算法处理此不足最有效的方法为选择重要性函数和使用重采样方法［18-20］。

选取重要性函数的目的是要使重要性权重的方差最小，在本文中将状态变量的转移概率密度函数作为重要性概率密度函数，即：q（x0：k｜y1：）k＝p（xk｜xk－1）。

为了弥补权值退化的不足，Gordon等提出重采样方法，使得PF算法又重新得到人们的重视，重采样的思想即减少权重小的粒子数，增加权重较大的粒子数，此过程是对后验概率密度函数再采样N次，得到新的支撑点集合，重采样操作得到的粒子独立同分布，且采样点被重新赋予的权值是相等的，然而重采样方法也往往带来负面的影响即样本枯竭，因此我们需要考虑退化程度问题，当PF滤波退化到一定程度时才应考虑重采样。通过有效粒子数Neff来衡量粒子退化程度，按下式进行选取：

滤波前预先设定一个阈值门限Nthres，有效粒子数的值必须大于设定的阈值Nthres，否则重采样；然后根据有效粒子数对应的归一化权值更新粒子集。

1.3 低频振荡信号去噪实现

通过获取电力系统低频振荡时的信号，根据信号建立状态方程和观测方程，根据先验概率密度p（x0：k）得到采样粒子，对粒子集进行初始化及重要性采样，通过重要性密度函数生成样本，对样本计算权值及归一化权值，判定是否进行重采样，迭代结束后得到粒子的最优状态估计，从而达到对原始信号去噪的结果。

在电力系统中，调度部门关注的是低频振荡的各个模式，为调度人员提供必要的信息，使得能够对低频振荡进行一定的抑制。在对低频振荡模式进行辨识前，通过使用粒子滤波去除信号噪声，还原出信号的特征，提高了接下来的模式辨识的精度。

2 基于EEMD的模式辨识

对去噪后的信号通过EEMD［21-24］方法进行模式辨识。基本思想为通过叠加高斯白噪声后的多次EMD分解。向原始信号加入频率均匀的白噪声背景时，不同时间尺度的信号区域都能自动映射到和背景白噪声相关的合适的尺度上。通过不相关随机序列的统计均值为0，对多次加入噪声后的总体取均值后，噪声将会被消除，总体均值被认为是信号本身，达到消除模态混叠问题。算法主要步骤为：

1）给原始信号x（t）中多次加入等长度随机正态分布的白噪声ni（t）（白噪声标准差为原始信号标准差的0.1～0.4倍）即：

式中xi（）t为第i次加入高斯白噪声的合成信号。所加噪声的幅度会直接影响EEMD的分解效果，如果幅度过小，噪声将失去补充尺度的作用，无法构成不同频率上的连续性。

2）将xi（）t分别进行EMD分解，得到各个IMF分量记为 Cij（t），与一个余项记为 rin（t），则有：

3）重复步骤1和步骤2操作N次。将以上各个IMF进行总体取均值运算，得到最终的IMF分量组为：

式中Cj（）t表示EEMD分解后得到最终的第j个IMF分量。N表示加入高斯白噪声的总体个数，总体个数越大，对应的白噪声的IMF和将更接近于0，得到的结果也更趋近于真实值。

将分解出的各阶IMF分量Cj（）t进行Hilbert变换可得：

可以得到瞬时相位 θi（t）、角频率 ωi（t）、频率fi（t）如下：

3 基于粒子滤波的EEMD分解

本文所述方法，将粒子滤波作为前置单元，去除非线性、非高斯低频振荡信号的噪声，基于上两节的理论，算法流程图如图1所示，本文方法的主要步骤如下：

（1）根据低频振荡信号建立粒子滤波的状态方程和观测方程，如式（1）和式（2）；

（2）初始化；k＝0，从先验概率密度 p（x0：k）采样得到采样粒子；

（3）重要性采样：在采样粒子中依据重要性密度函数 q（x0：k｜y1：k）中随机抽取N个有限的样本；

（4）对抽取的N个样本利用式（4）计算相对应的权值wk；

（5）将步骤3得到的权值根据式（5）进行归一化处理，得到归一化权值

（6）利用式（7）判定重采样：有效粒子数的值必须大于设定的阈值Nthres，否则重采样，继续返回步骤（2）继续执行；

（8）对去噪后的信号使用EEMD进行分解，得到IMF；

（9）对 IMF进行 Hilbert变换，根据式（11）～式（14）计算得出各个IMF的瞬时频率，从而辨识出低频振荡模式。

图1 算法流程图Fig.1 Algorithm flow chart

4 算例分析

为测试本方法对低频振荡模式辨识的有效性，取以下信号（单位为MW）：

该信号包含三个振荡模式，频率分别为0.7 Hz，1.5 Hz，0.5 Hz，该信号包含信噪比SNR为20 dB的高斯白噪声ω（n），利用粒子滤波作为前置滤波单元，对上述信号进行去噪处理，首先分别建立粒子滤波所需的状态方程和观测方程，将原始信号s（t）作为状态方程，而观测方程则由原始信号加上随机噪声得到如式（16）、式（17）所示。

式中的xk与yk分别表示系统的状态量和观测量，并且假设初始状态值为x0＝0.1，初始状态分布p（ x0） ～N（0，1），观测噪声 rk～N（0，5），时间迭代步长为50，粒子数 N＝1 000，定义有效区间为［5，95］，为了防止边界效应的影响，在下述操作过程中将区间扩大为［0，100］，根据以上参数进行粒子滤波去噪处理，其仿真结果如图2所示。

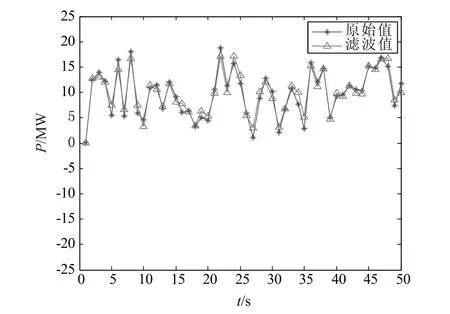
图2 粒子滤波去噪结果Fig.2 Particle filtering de－noising results

根据图2可以看出，经过粒子滤波去噪后的信号基本可以与原信号很好的吻合，误差较小，基本保留了原始信号的特征，去噪效果较好。因此，使用粒子滤波对信号进行去噪处理是有效的、精确的。

为进一步辨识出信号的低频振荡模式，对去噪后的信号使用改进的EMD方法EEMD来进行分解，分解得到3个IMF1～IMF3结果如图3（a）～图3（c）所示。

图3 EEMD分解后的各IMF分量Fig.3 IMFs by EEMD decomposition

对得到的IMF1～IMF3进行提取瞬时频率参数操作，提取的IMF1～IMF3的瞬时频率结果如图4（a）～图4（c）所示。

经过上述操作后得到的瞬时频率存在边界效应，为了更好的对低频振荡模式进行识别，减少边界效应对最终模式辨识的结果影响，对得到的瞬时频率f1～f3在有效区间［5，95］内进行求均值处理，各瞬时频率的均值见图4（a）～图4（c），结果如下所示。

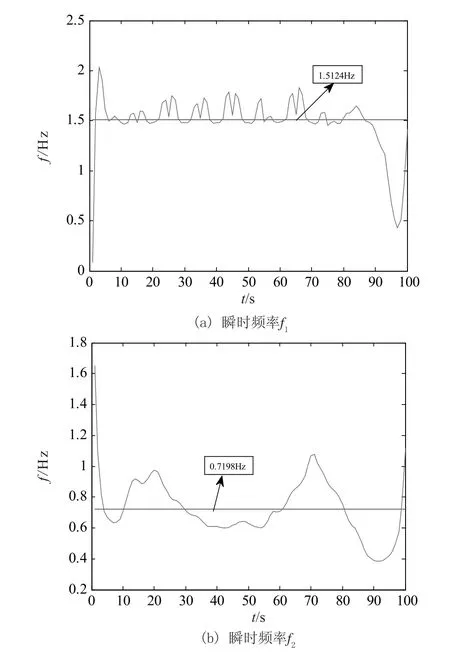
图4 IMF分量得到的瞬时频率Fig.4 Instantaneous frequency of the IMF component

由表1可知，原信号中包含了三个振荡模式，存在两个局部振荡模式和一个区域振荡模式，这与文献［25］中所用方法得到的结果一致。因此，本文所述方法可以很好的去除噪声，辨识出低频振荡模式，并且误差较小。

表1 取均值后频率与理想参数对比Tab.1 Comparison of the frequency after averages and the ideal parameter

为进一步测试本文方法的有效性和正确性，采用Prony分析法对上述信号进行模态辨识处理。取采样频率为fc＝50 Hz，采样点数N＝500，模型阶数p＝18，得到Prony分析的模式辨识结果如下所示。

图5 Prony算法Fig.5 Prony algorithm

表2 Prony方法辨识结果（频率单位：Hz）Tab.2 Prony method identification results（frequency unit：Hz）

由图5及表2可知，根据Prony算法辨识非线性、带噪声的信号时，对噪声及非线性情况比较敏感，辨识出的结果误差较大，无法准确的辨识出振荡模式，而本文方法在此种情况下，适用性更好，更能较好的辨识出在带噪声的非线性信号的振荡模式。但在本方法中，经过粒子滤波及EEMD分解后，得到的瞬时频率存在边界效应，存在误差，导致计算精度存在不足，在后续研究中，将把减小边界效应的影响作为研究的方向。

6 结束语

本文提出一种基于粒子滤波与EEMD的低频振荡模式辨识的新方法，在对粒子滤波算法进行详细的分析与探讨之后，利用粒子滤波作为前置滤波单元，对信号进行去噪处理后，再使用EEMD对去噪后的信号进行分解得出低频振荡模式。从算例结果可以得出本文所提方法能够很好的还原初始信号的特征，证明了本方法的准确性及精确性。

PF算法是一种非线性统计算法，能够适用于非线性非高斯系统的去噪、状态估计等，在滤波精度和稳定度上都具有较大的优势，具有良好的应用前景，粒子滤波算法计算效率的提高和有效处理边界效应是今后研究的方向。